LoginSignup
7
2

More than 3 years have passed since last update.

@convto

Wu らによる差分検出の O(NP) アルゴリズム実装シリーズ ②探索方法

Last updated at Posted at 2019-12-24

はじめに

これは、3回にわけて Wu らによる O(NP) アルゴリズムを解説、実装するシリーズです。

の3部に分かれています。

今回も、前回に引き続き Wu らによる O(NP) アルゴリズムの解説をしていきたいと思います。
前回の ①仕組み、考え方編 では、大まかな考え方を整理して、なぜ計算量が下がるのかわかりました。
今回は、前回わかったことを利用して、実際にどう探索していくのかまとめていきます。

元論文は An O(NP) Sequence Comparison Algorithm by described by Sun Wu, Udi Manber and Gene Myers です。興味のある方はそちらも目を通すと面白いと思います。

最終的な実装を確認したい方は https://github.com/convto/onp に置いてあるのでそちらをごらんください。

これは Makuake Development Team Advent Calendar 2019 - Adventar の19日目の投稿です(遅くなりました)

前回のおさらい

①仕組み、考え方編 でわかっている部分を以下にまとめます。

  • 入力A,B の長さをそれぞれ M, N とする(このとき M <= N )
  • Δ = N - M とする
  • 削除の合計回数を P とする
  • 編集距離Dは D = Δ + 2P で求めることができる
  • kのとりうる範囲は k ∈ [-p, Δ+p]

今回は、これらのわかっている情報を利用しつつ、探索方法について説明していきます。

探索方法

この探索の目的は、一番短い編集距離を求めることです。
一番短い編集距離さえわかれば、その時たどったルートを求めればSESが、一致した文字列を取得すればLCSが取得できます。

前に述べた D = Δ + 2P より、 Δ と P がわかれば D は導けます。
Δ は入力A,Bを受け取った時点で確定するので、あとは P さえわかれば D が導けます。
つまりこの探索の目的とする処理は

M <= N で p ∈ [0, M] としたときに、エディットグラフ上の点(M,N)にたどり着く手順のうち最も小さいPの値を求める処理

と言えそうです。

ざっくり以下のように考えます。

  1. Pの値を探索
  2. ループ内の処理で そのP値のときの取りうる点のうちk上に斜めに進める限り進んだもの を求める
  3. 最初に点(M,N)にたどり着いたときのP値は点(M,N)につくための最も小さいP値のうちの一つ
  4. 3 から、このP値のときに求まる D (D は Δ + 2P) が最も小さい編集距離の一つ
  5. 4 のときの編集手順がSES、最長一致する文字列がLCS

そのP値のときの取りうる点のうち斜めに進める限り進んだもの を求めるのはなぜでしょうか。かるく整理しましょう

なぜ k 上の最も進んだ点を求めるの？

考えを整理するために、以下にある入力A,Bがある 点(M,N) にたどりつくまでのP値を、対応する座標に書き込んだグラフを書きます1
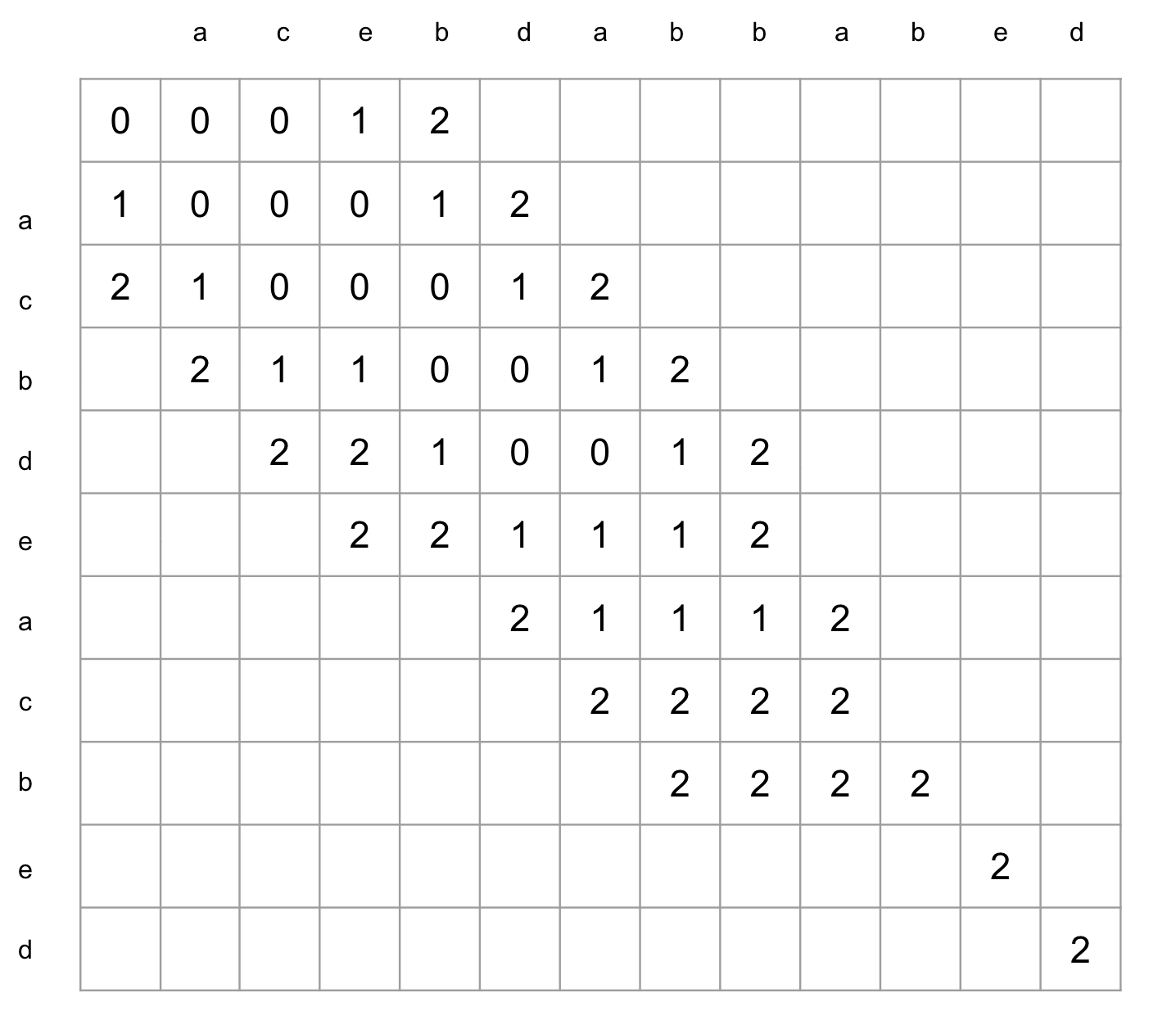
スクリーンショット 2019-12-25 1.57.15.png

この図の例では P = 2 のときに点(M,N)に到着します。
隣接しているマスへは、それぞれ

  • 横(挿入した場合、編集距離+1)
  • 縦(削除した場合、編集距離+1)
  • 斜め(一致した場合、編集距離±0)

の編集をすれば移動できます。
このとき、斜めに進める場合は編集にコストがかからない(=Pは増加しない)ことに注目してください。
斜めは編集コストをかけずに 点(M,N) に近づけるため、最短編集距離を求める観点からは進める限り斜めに進んだほうがよいです。

斜めに進めるだけ進んだときの最後の点を求める、ということは k = y - x としたとき、あるk上の到達可能な最遠点 を求めるということです。

前回のまとめから、あるPには取りうるkの範囲があるのでした。
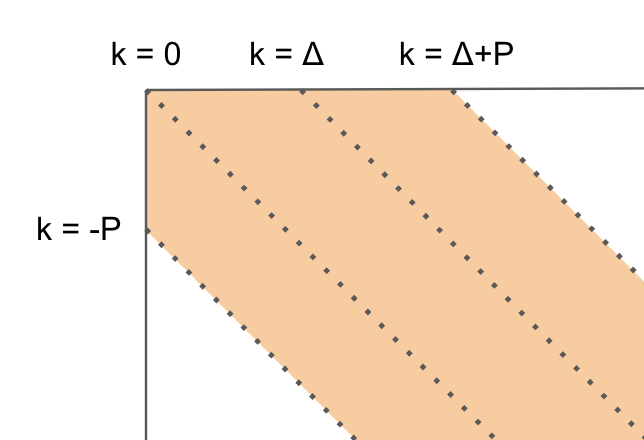
スクリーンショット 2019-12-25 0.51.47.png
図のように、kの取りうる範囲は k ∈ [-p, Δ+p] です。

あるPが取りうる複数のkにおいて、それぞれのkの到達可能な最遠点を求めらると、なにが嬉しいのでしょうか？
P = 2 として、先程のPの値を網羅した図にそれぞれのkの最遠点に印をつけると、以下のようになります。
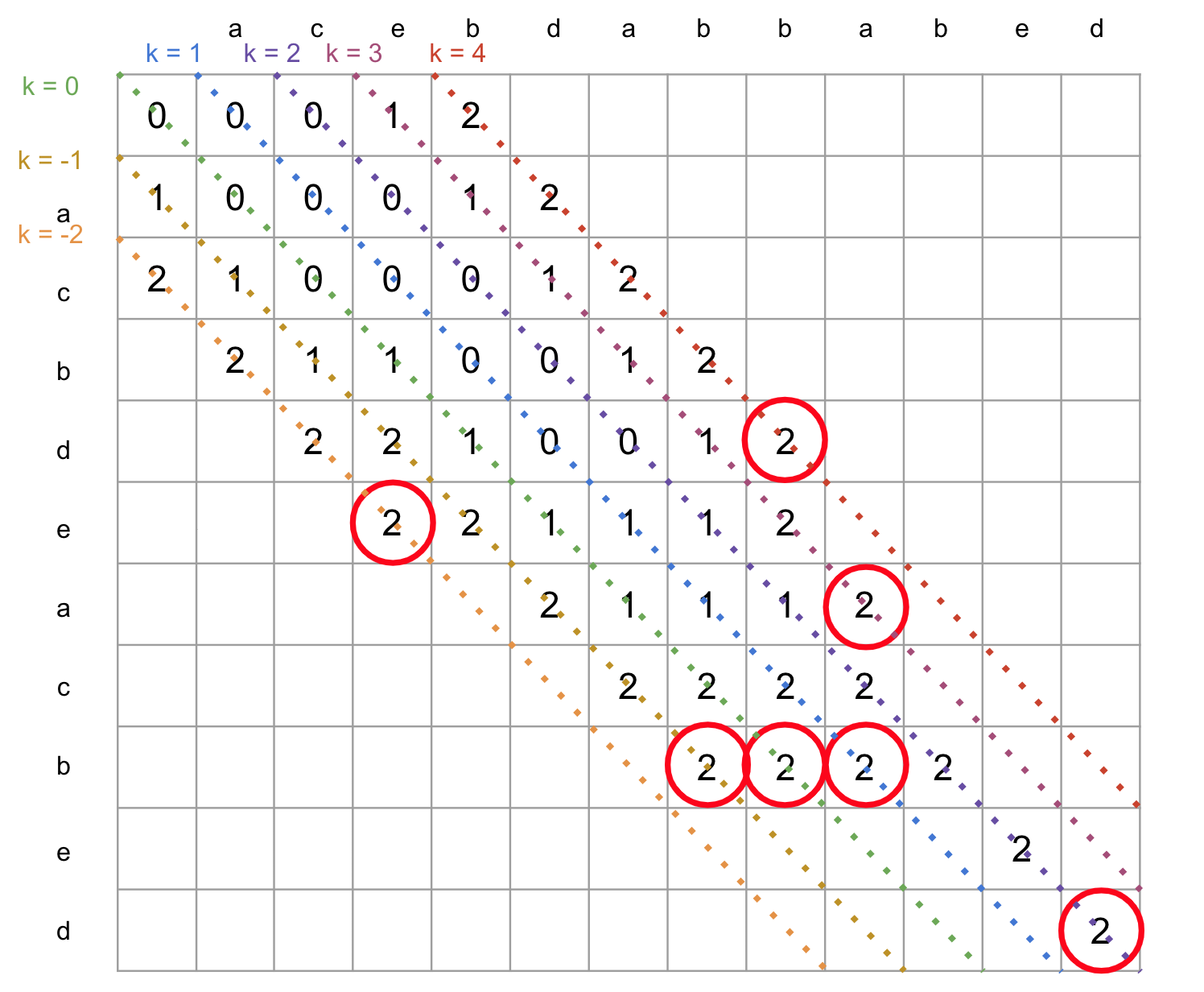
スクリーンショット 2019-12-25 2.16.26.png

このとき求めたk上の取りうる最遠点に 点(M,N) が含まれていればそのときのPが取りうる最も少ない削除回数です。
D = Δ + 2P から、このときのPを利用すれば最も編集手順が少ない場合の編集距離が求められます。

この例の場合は P = 2 のとき 点(M,N) に到着していますね。
D = 2(Δの値) + 2 * 2(点M,Nに到着する最も少ないP) なので、この例で最短となる編集距離は6です。

つまり あるP値のときの取りうる点のうちk上に斜めに進める限り進んだものを求める理由 は、それを繰り返して 点(M,N) を満たすまで探索を続けることで編集距離を求めることができるからです。

fp(k,p) の定義

ある p, k のときに取りうる最も斜めに進んだ点、言い換えると k 上の最遠点を fp(k,p) とします。
fp(k,p) は最遠点のy値を返します。
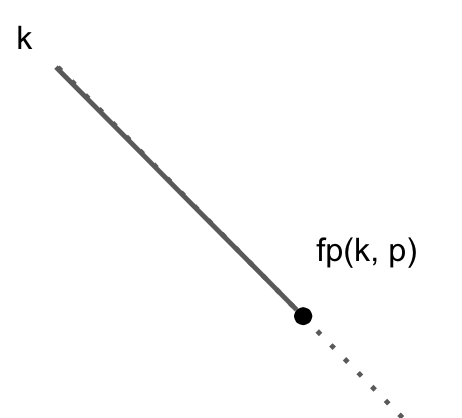
スクリーンショット 2019-12-25 2.26.34.png

点の情報なのになぜy値しか返さないかというと k = y - x より x = y - k で求めることができ、呼び出し側でx軸の値については解決するからです。
元論文でもx値は省略されています。

これまでの内容を擬似コードにするとこうです

dummy.code
for (p = 0; p <= M, p++) {
    for (k = -p; k <= Δ + p; k++) {
        fp[k][p] = k上の最遠のy値を求める処理()
    }
    if (fp[Δ][p] == N) {
        // k が Δ上で N までたどり着く、つまり点(M,N)に到着していた場合
        return Δ + 2*P // Dの値を返す
    }
}

あとは k 上の最遠点が求められれば良いです。
今回定義した fp(k,p) を求める方法を見ていきましょう。

fp(k,p) の求め方

k上の最遠点を求める、ということはどれだけ斜めに進めるのか調べて、斜めに進めなくなったらその点を返す、ということです。
先程述べたとおり、yだけ取得すればxは導けるので、返すのはyの値だけで良いです。

エディットグラフで斜めに進めるのは文字A[x],B[y]が一致したときだけです
最遠点を求めるので、これを可能な限り、つまりx++, y++ して成立する限り繰り返します
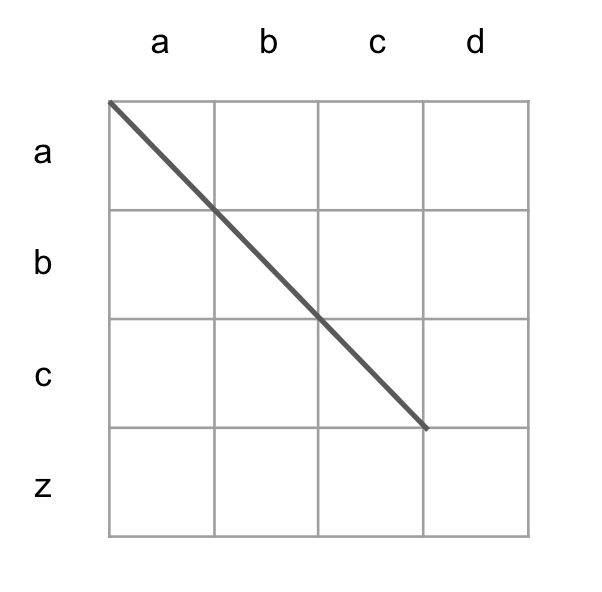
スクリーンショット 2019-12-25 2.50.52.png

この例では d, z が一致しないので 点(3,3) が到達可能な最遠点になります。

このように、開始位置となる点を入力すると斜め方向に進めるところまで進んで、最遠点のy値を返す処理を snake(k,y) とします。
入力と戻り値に x がないのは、これまでと同じように x = y - k より求められるので省略しています。

これまでの流れを整理すると以下のようになります。

dummy.code
a = 入力A
b = 入力B

for (p = 0; p <= M, p++) {
    for (k = -p; k <= Δ + p; k++) {
        fp[k][p] = snake(k, 開始位置のy)
    }
    if (fp[Δ][p] == N) {
        // k が Δ上で N までたどり着く、つまり点(M,N)に到着したら
        return Δ + 2*P // Dの値を返す
    }
}

// 他にも考慮事項がありますが、現時点では斜めに進めるか検証するのみ
snake(k, y) int {
    x = y - k
    while (a[x] == b[y]) {
        x++
        y++
    }
    return y
}

snake に渡す開始点のy値がわかればDの値が導けそうですね。ここまでくればあと少しです。

snake(k,y) のy値の求め方

任意のk,pのとき、どのようにして snake(k,y) のy値を求められるでしょうか。
まず、初期位置yの値はとりうる最大のものでなければなりません。
これは、とりうる初期位置のうち最も大きいy値を与えないと snake(k,y) が k 上の最遠点を導けない場合があるからです。
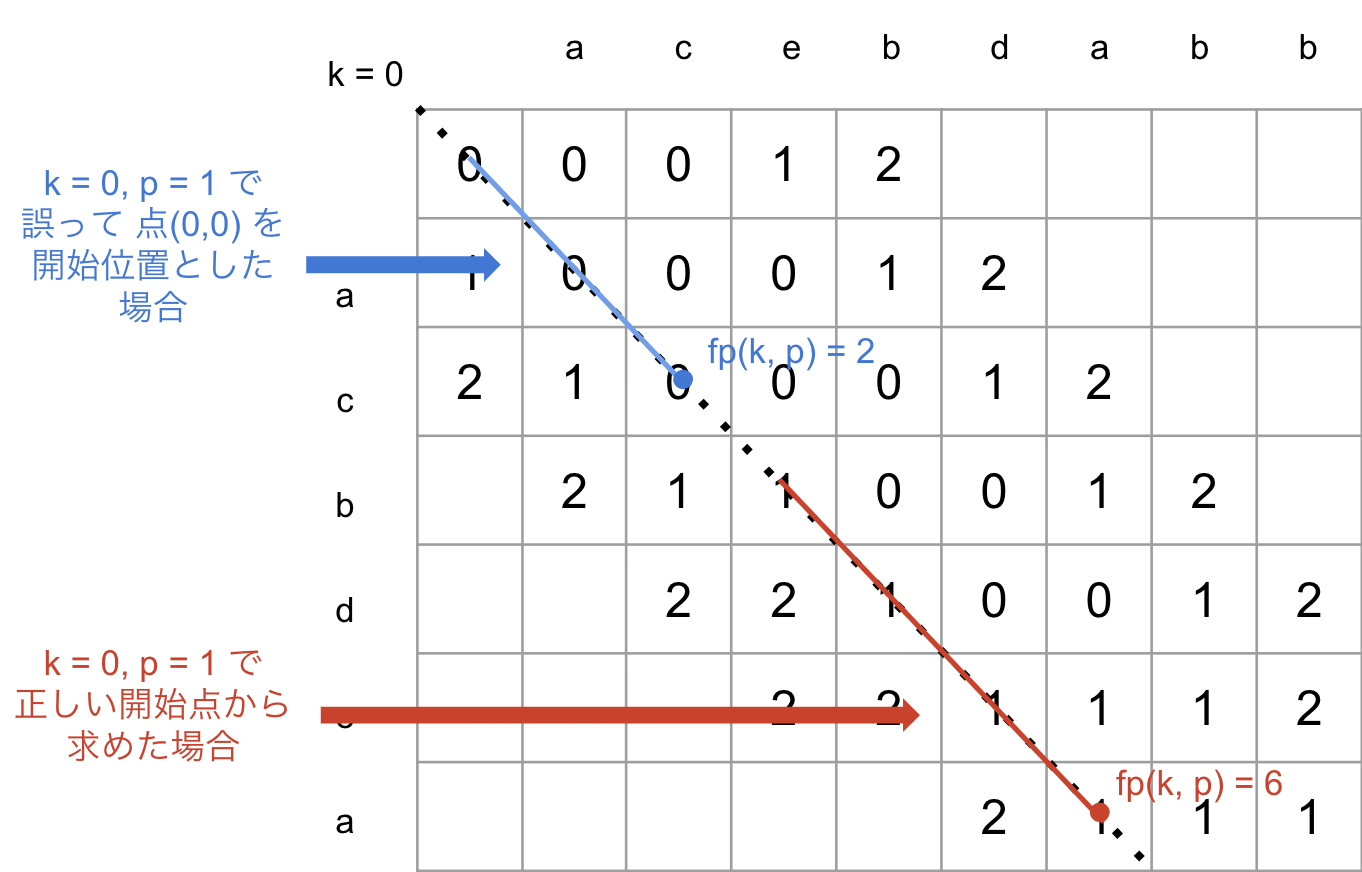
スクリーンショット 2019-12-25 3.09.55.png

初期位置には以下の2パターンあります。

  • ① k-1 の最遠点からy方向(挿入方向)に移動して k 上にのる場合
  • ② k+1 の最遠点からx方向(削除方向)に移動して k 上にのる場合

①は k-1 のときの snake の結果( k-1 の最遠点のy値)からy方向に移動した k 上の点です。
②は k+1 のときの snake の結果( k+1 の最遠点のy値)からx方向に移動した k 上の点です。

どちらも、隣接するkの最遠点から挿入もしくは削除の手順を伴い k 上に移動してくるということです。
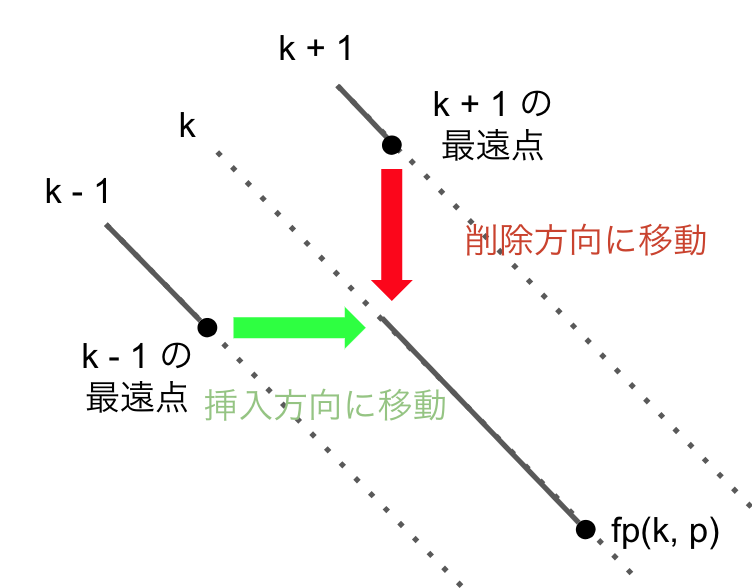
スクリーンショット 2019-12-25 3.20.23.png

snake には取りうる最大の値を与えたいので、これらの方法で取得した k 上に合流する2つの点のy値のうち、より大きい方を snake(k,y) に与えればよいです。

注意としては、①の挿入手順でk上に合流するときは合流のために y 方向に 1 足した値が k 上のsnake初期位置のy値になります。

②のときは、合流には x 方向に進むのみで y の値は変化はないので k+1 上の移動元の点のy値を使います。
②のときもxに加算しないとおかしいように思いますが、これも今までのように x = y - k で合流後のx値は求められるので、考慮しなくともよいです。

ある値k上の最遠点を求める snake(k,y) の呼び出し方について、今述べた注意事項をふまえて擬似コードを書くと、以下のようになります

dummy.code
fp[k][p] = snake(k, max(k-1の最遠点のy値 + 1, k+1の最遠点のy値))

k上の最遠点をもとめるsnake処理をするためには、k+1, k-1 の最遠点がわかればよいです。
このとき気をつければならないことは、kと隣接する

  • k-1 上の最遠点 fp(k-1, p) + 1
  • k+1 上の最遠点 fp(k+1, p)

を求めるときのp値が等しいと、k の値によってどちらか一方が k 上に接続できない場合があることです。
詳しく説明します。

k ∈ [-p, Δ-1] の場合

例えば k ∈ [-p, Δ-1] の場合です。
このような範囲です
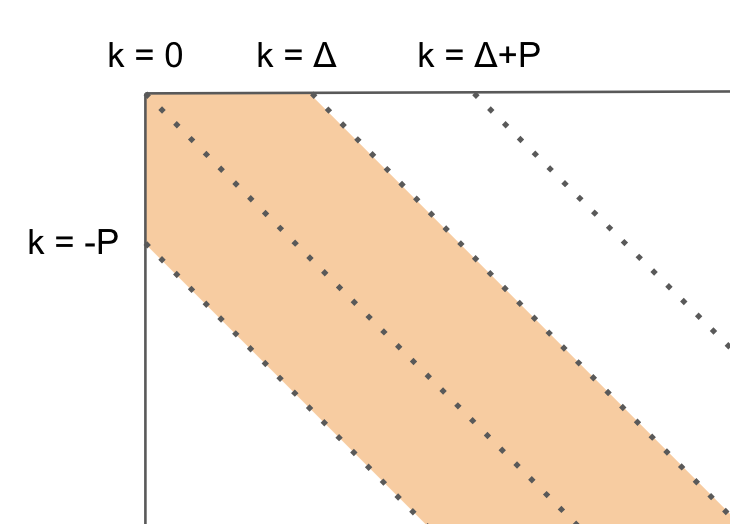
スクリーンショット 2019-12-25 3.24.43.png

この領域では削除したときにp値が増え、挿入は削除した分のΔへの復帰なのでpが増えません。
これは、この領域だとx方向への移動がΔ線上から離れていく操作となるためです。
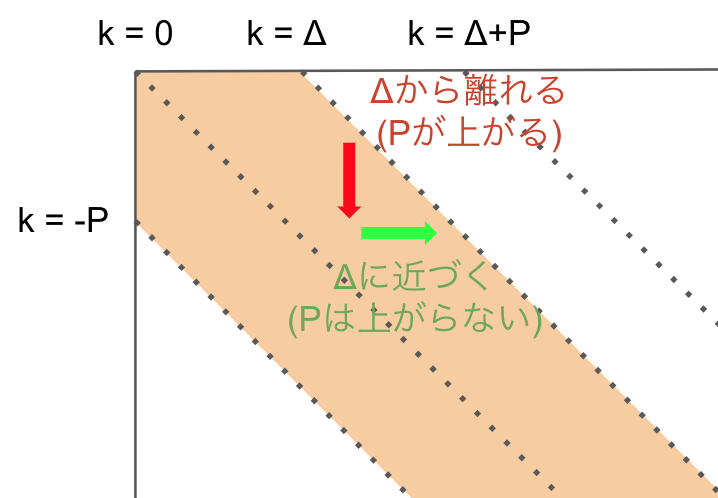
スクリーンショット 2019-12-25 3.30.50.png

下に移動すると p が1上がるということは、k上の点と接続可能な k+1 上の最遠点は p-1 のときのものでないと接続できません。

以上のことから、以下のように言えます。

k ∈ [-p, Δ-1] のとき、
fp(k,p) = snake(k, max(fp(k-1, p) + 1, fp(k+1, p-1)))

k ∈ [Δ+1, Δ+p] の場合

つぎに k ∈ [Δ+1, Δ+p] の場合です。
このような範囲です
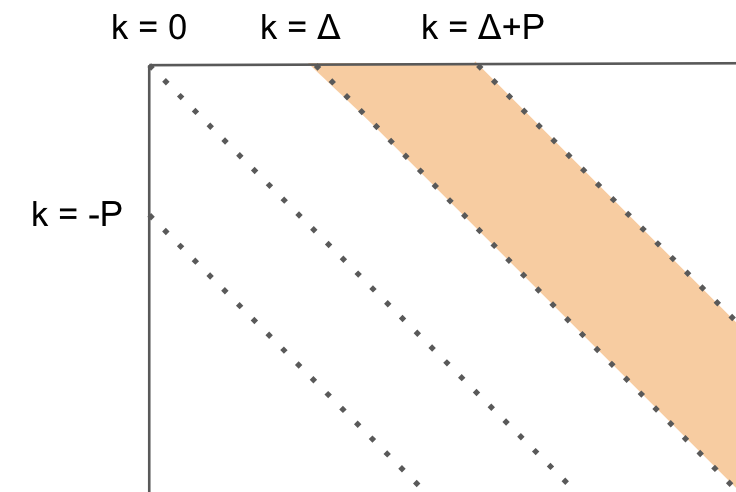
スクリーンショット 2019-12-25 3.39.02.png

この領域では挿入したときにp値が増え、削除は挿入した分のΔへの復帰なのでpが増えません。
これは、この領域だとy方向への移動がΔ線上から離れていく操作となるためです。
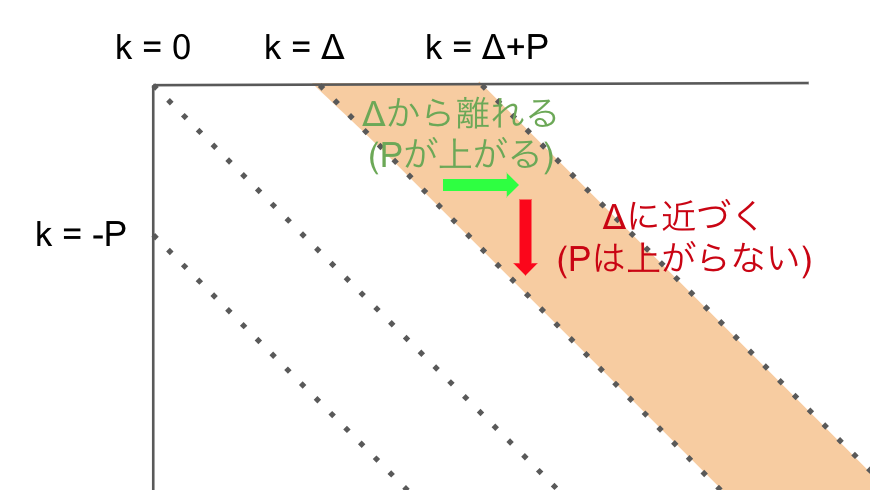
スクリーンショット 2019-12-25 3.37.50.png

右に移動すると p が1上がるということは、k上の点と接続可能な k-1 上の最遠点は p-1 のときのものでないと接続できません。

以上のことから、次のように言えます。

k ∈ [Δ+1, Δ+p] のとき、
fp(k,p) = snake(k, max(fp(k-1, p-1) + 1, fp(k+1, p)))

k = Δ の場合

最後に k = Δ の場合です。
これは、k がちょうどΔ上にある場合です。
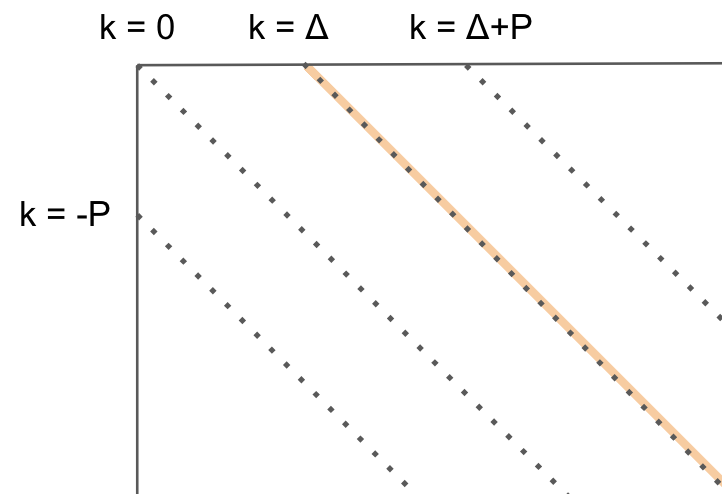
スクリーンショット 2019-12-25 3.41.30.png

  • k-1 (Δより1小さいので k ∈ [-p, Δ-1] に当てはまる) の最遠点
  • k+1 (Δより1大きいので k ∈ [Δ+1, Δ+p] に当てはまる) の最遠点

のどちらから移動されても、Pが増えることはありません。どちらの操作もΔに近づく移動となるためです。
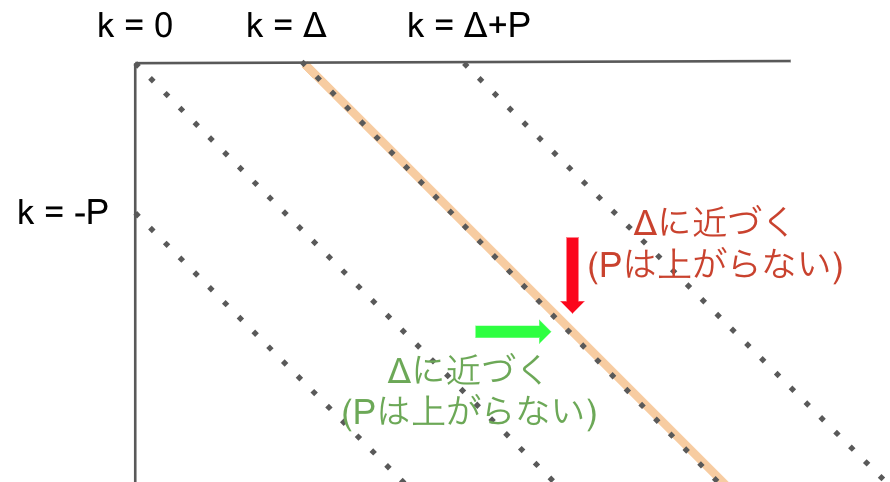
スクリーンショット 2019-12-25 3.43.47.png

そのためこの領域では、一つ前のpのときの最遠点を考慮する必要はありません。
よって以下のことが言えます

k = Δのとき、
fp(k,p) = snake(k, max(k-1, p) + 1, max(k+1, p))

snake(k,y) を使った fp(k,p) の表し方

これらのことより、fp(k,p) は k の範囲によって求め方が異なり、以下のように表せます

          snake(k, max(fp(k-1, p) + 1, fp(k+1, p-1)))  (k ∈ [-p, Δ-1])
fp(k,p) { snake(k, max(k-1, p) + 1, max(k+1, p))       (k = Δ)
          snake(k, max(fp(k-1, p-1) + 1, fp(k+1, p)))  (k ∈ [Δ+1, Δ+p])

これを当てはめ、今までの処理を擬似コードで表現すると

dummy.code
a = 入力A
b = 入力B

for (p = 0; p <= M, p++) {
    k ∈ [-p, Δ+1] {
        fp[k][p] = (k, max(fp(k-1, p) + 1, fp(k+1, p-1)))
    }
    k = Δ {
        fp[k][p] = snake(k, max(k-1, p) + 1, max(k+1, p))
    }
    k ∈ [Δ+1, Δ+p] {
        snake(k, max(fp(k-1, p-1) + 1, fp(k+1, p)))
    }
    if (fp[Δ][p] == N) {
        return Δ + 2*P // Dの値を返す
    }
}

snake(k, y) int {
    x = y - k
    while (a[x] == b[y]) {
        x++
        y++
    }
    return y
}

これで探索方法がわかりました！
ここまでまとまれば実装できそうですね、このアルゴリズム思いついた人すごすぎる...

今回のまとめ

今回は、考えを少しづつ積み重ねて探索方法の大枠がわかりました。

このくらい複雑な操作をしだすと、エディットグラフの利点が活きてきますね。
削除、編集などの手順を x, y 方向への移動に翻訳できるので、数値の演算としてそれらの操作を行えるのが

  • 数学的に考えを積み重ねる観点
  • プログラムとして実装する観点

のどちら絡みても、とても都合が良いです。

ここまでわかってくれば他の差分検出アルゴリズムの学習もスムーズに進むと思うので、興味がある方は他のアルゴリズムの学習をしても良いかもしれませんね！

次回は、ここで整理した大まかな擬似コードをもとに、Go言語で実装していく回になります。
この複雑で難しいアルゴリズムが、たった数十行のコードで表現できるのはとてもおもしろく、同時にとても不思議な気持ちになります。

次回は ③Goによる実装 です、次の記事もお付き合いいただけると幸いです。

参考文献

  1. 余談ですがこのグラフは元論文とおなじ入力A,Bを利用しています。多すぎず少なすぎず、単純すぎず複雑すぎない、非常にいい入力の例だったためです ↩

7
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
2