概要
この記事は数値計算 Advent Calendar 2018の4日目の記事です。
本記事では準モンテカルロ法(Quasi-Monte Carlo, QMC)というアルゴリズムを紹介します。
準モンテカルロ法は、高次元の超立方体$[0,1]^s$上の関数を数値的に積分するためのアルゴリズムです。
積分ノードを「超一様性」を重視して選ぶことで、次元の呪いの回避とモンテカルロ法よりも高速な収束を目指します。
追記:この記事を発展させた日本語のサーベイ論文が出版されました。
次元の呪い
$[0,1]^s$上の関数を数値積分しようと思ったとき一番単純なアルゴリズムは、
「$[0,1]^s$の各辺を$N$分割してできた、$N^s$個の各小ブロックの中心での関数値を平均する」
方法です。つまり、区分求積法の$s$次元直積です。
しかしこの方法だと、高次元の場合は計算量が爆発してしまいます。たとえば、$N=10$、つまり立方体の各辺を$10$分割したとしましょう。$1$次元の場合はたった$10$個の値の平均をとればいいわけですが、たとえば$s=10$次元の場合、分割された小ブロックの個数はすでに$10^{10}$となり、たかが各辺を$10$分割した程度の精度の悪い計算に十数秒かかります。$s=20$とすると、$10^{20}$回の演算が必要ですが、これはもう生きている間には終わりません。このように、次元に対して指数的に計算量が増えていってしまう現象を次元の呪いと呼びます。
1次元積分法として区分求積法よりも精度の高い積分法が(シンプソン則、ガウス・ルジャンドルなど)
知られていますが、$s$次元に拡張するときに積分則の単純な直積を考える限り、次元の呪いからは逃れられません。(単純な直積ではない方法としてスパースグリッドがあります。ここではとりあげません)
モンテカルロ法
次元の呪いを回避する数値積分法として有名なのがモンテカルロ法です。
モンテカルロ法は、「定まっている値を求めるためにランダムネスを使う」方法です。
つまり、$N$個の点$x_0, \dots, x_{n-1}$を$[0,1]^s$から独立一様ランダムに選び、
$$
\frac{1}{N}\sum_{i=0}^{N-1} f(x_n)
$$
を近似値として採用します。驚くべきことに、積分誤差の収束オーダーは$O(1/\sqrt{N})$となり、(明示的には)次元$s$に全く依存しません!しかしながら、モンテカルロ法の収束速度では$1$桁精度をよくするために$100$倍の計算が必要であり、実用的ですが十分な収束速度とはいえません。
とくに、「関数の性質のよさ」という情報を全く使っていない点が悔しいです。極論、$f$が一次式で表せるとわかっていた場合、$f$の積分値は立方体のど真ん中の点での関数値に一致するので、計算コストほぼゼロで積分値を当てることができますが、モンテカルロ法では関数にかかわらず収束オーダーは$O(1/\sqrt{N})$です。
準モンテカルロ法
準モンテカルロ法(以下QMCと略します)は、次元の呪いを回避しつつ、モンテカルロ法より高速な誤差の収束を目指します。アルゴリズムの大枠はモンテカルロ法と同じです。
つまり、$N$個の点$x_0, \dots, x_{n-1} \in [0,1]^s$における関数値の平均値
$$
\frac{1}{N}\sum_{n=0}^{N-1} f(x_n)
$$
を近似値として採用します。しかし、モンテカルロ法と違い、積分ノードにランダム性はありません。
その代わりに、積分ノードが「超一様」になるように設計します。
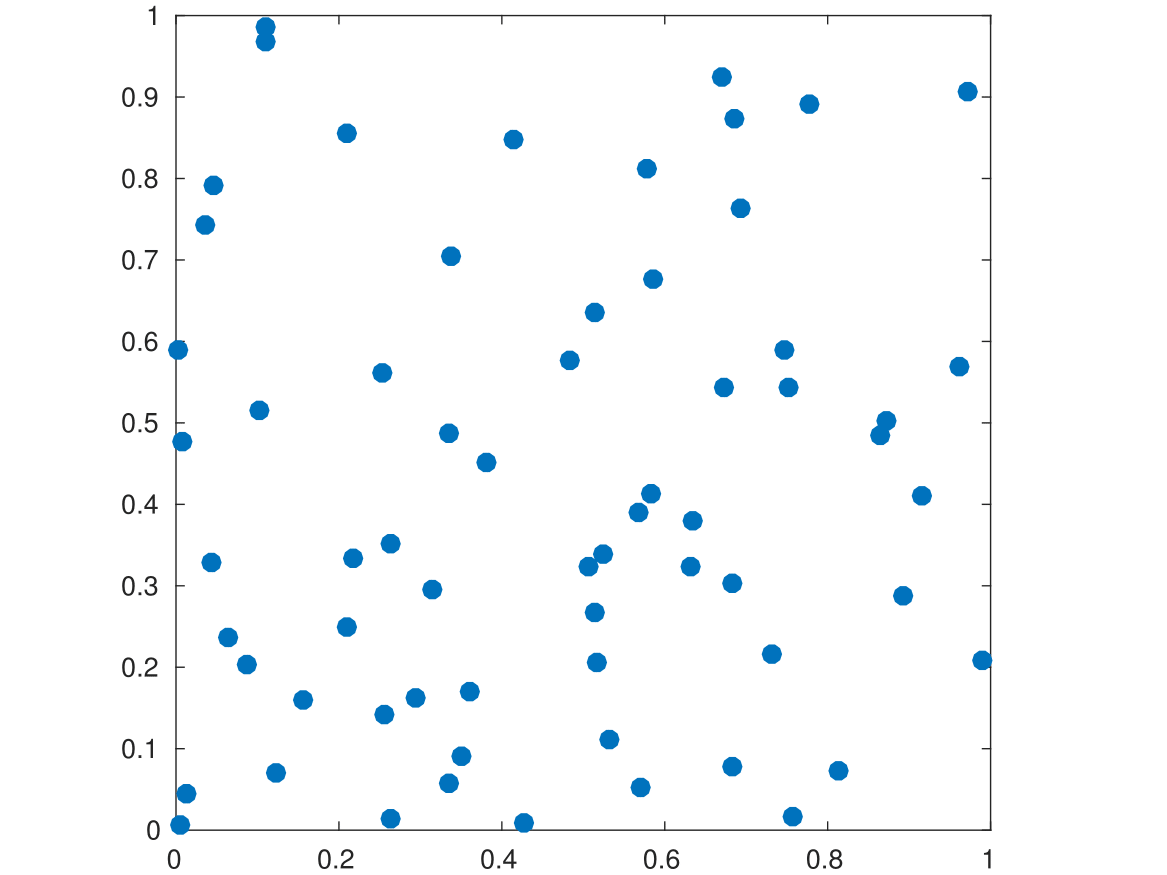
上の図のうち、左が乱数によるモンテカルロ点集合、右がSobol列と呼ばれるQMC点集合です。
なんとなく右のほうが一様っぽく見えるとおもいます。
以下では数学的に一様性や積分誤差の収束を見ていきます。
数論や解析が思わぬところで顔を出すのが、この分野の魅力です。
一様分布論とディスクレパンシー
いきなりですが定理です:$x_n$を$n \sqrt{2}$の小数部分としたとき、点列 $(x_i)$ は$[0,1]$上に一様に分布します。ここで、点列が一様に分布するとは、任意の区間$[a,b]$を固定したときに、「$x_0$から$x_N$までで区間$[a,b]$に入る点の割合」が、$N$を無限大に飛ばしたときに$b-a$に収束する、ということです。Weylはこの定理を、「任意の周期的な三角関数$f$に対して
$$
\lim_{N \to \infty} \frac{1}{N} \sum_{i=1}^N f(x_i) = \int_0^1 f(x) , dx
$$
が成り立てば、点列$(x_n)$は$[0,1]$上に一様に分布する」という、一様性と積分近似を結びつける (!) 定理を介して証明しました。
いまでは一様分布列の概念は、むしろ以下のように積分近似のほうから定義することも多いです。
無限点列$x_0, x_1, \dots, \in [0,1]^s$をとります。任意のリーマン可積分関数 $f \colon [0,1]^s \to \mathbb{R}$ に対して
$$
\lim_{N \to \infty} \frac{1}{N} \sum_{i=1}^N f(x_i) = \int_{[0,1]^s} f(x) , dx
$$
が満たされるとき、この点列を一様分布列といいます。
一様分布列を使った数値積分は、いつかは真の値にいくらでも近づくことができます。その「いつか」がいつ訪れるのかを調べるためには、一様性を定量化する必要があります。そのひとつが点集合のディスクレパンシー (discrepancy)です。ディスクレパンシーは、差異、くい違いといった意味の言葉です。お堅くいうと「非一様度」でしょうか。アイデアとしては、特定のテスト関数の集合をとってきて、テスト関数のQMC積分誤差の最大値を点集合のディスクレパンシーとします。テスト関数のとり方に応じて、それぞれのディスクレパンシーが定義されます。
とくによく使われるのが、star-discrepancyとよばれる、
「原点を左下の点にもつ直方体の特性関数」をテスト関数にとったディスクパンシーです。
$P=\{x_0, \dots, x_{N-1} \}$を$N$点集合とします。$P$の star-discrepancy$D(P)$は以下のように定義されます。
$$
D(P) = \sup_{a_1, \dots, a_s \in [0,1]} \left \lvert \frac{|I \cap P|}{N} - \mathrm{vol}(I) \right \rvert \qquad ただし I=[0,a_1) \times \cdots \times [0,a_s)
$$
star-discrepancyのテスト関数の線形結合でリーマン和に現れる区分的定数関数が作れるので、star-discrepancyが$0$に収束する点列は一様分布列です。
(追記:star-discrepancy は$D^{*}(P)$や$D_N^{*}(P)$という記法を使うことが多いです。Markdownとの相性のためここでは$D(P)$で通します)
Koksma-Hlawkaの不等式
star-discrepancyの定義に使ったテスト関数は直方体の特性関数なので、一見するとそれ以外の関数の積分誤差についてはなにも情報が得られないように見えます。実は、star-discrepancyと積分誤差をつなげるKoksma-Hlawkaの不等式が知られています。
$f \colon [0,1]^s \to \mathbb{R}$とし、$f$のHardy and Krauseの全変動を $V(f)$ とおきます。
(たとえば$\partial x_1 \cdots \partial x_s f$が連続(で可積分)のとき、全変動は有限値になります。)
このとき、以下の積分誤差を評価する不等式をKoksma-Hlawkaの不等式といいます:
$$
\left|\frac{1}{N} \sum_{i=1}^N f(x_i) - \int_{[0,1]^s} f(x) , dx \right|
\leq V(f) D(P)
$$
(つまり、全変動をノルムとするノルム空間上の線形作用素 $\mathrm{Err}(, \cdot, ;P)$の作用素ノルムが $D(P)$ と一致します。)
Koksma-Hlawkaの不等式のおかげで、全変動有界な関数に対しては$D(P)$ **を小さくすれば積分誤差が小さくなります!**つまり、積分誤差を、「関数のお行儀のよさ」と「点集合の一様性」の2つの要因に分離して考えることができます。
いよいよ $D(P)$ の小さい点集合が欲しくなってきました。
では、 $D(P)$ はどのくらい小さくできるのでしょうか?実は、空間の次元$s$を固定したとき、よい$N$点集合$P$が構成できてそのstar-discrepancyは
$$ D(P) \leq C(s) \frac{(\log{N})^{s-1}}{N} $$
をみたします。これぐらい高速に($O(N^{-1+\epsilon})$くらいで)ディスクレパンシーが小さくなる点集合の族をlow-discrepancy、もしくは超一様などと称します。超一様点集合をQMCの積分ノードに使えば、Koksma-Hlawkaの不等式と組み合わせることで、QMC積分誤差は$O(N^{-1+\epsilon})$で収束することがわかり、とくにモンテカルロ法よりも誤差が漸近的に高速に収束します。
これがクラシカルなQMCの理論です。
なお、star-discrepancyの下界としては、Rothによる
$$ D(P) \geq c(s) \frac{(\log{N})^{\frac{s-1}{2}}}{N} $$が知られています(最近もう少し強められた)。
上界と下界は$\log N$の指数部分のみが異なっていますが、その決定は長年の未解決問題です。
ここからは点集合の構成法をカンタンに紹介します。
QMC点集合の構成
ディスクレパンシーの小さな点集合として、ここでは格子とデジタルネットの2種類を紹介します。
格子
点の数$N$と、"生成ベクトル"の各要素$g_1, \dots, g_s \in \mathbb{Z}$が与えられたとき、
$n$番目の点$x_n$を
$$
x_n = \left(\frac{ng_1}{N}, \dots, \frac{ng_s}{N}\right) \mod 1
$$
として定めた$N$点集合$\{x_0, \dots, x_{N-1}\}$を格子といいます。
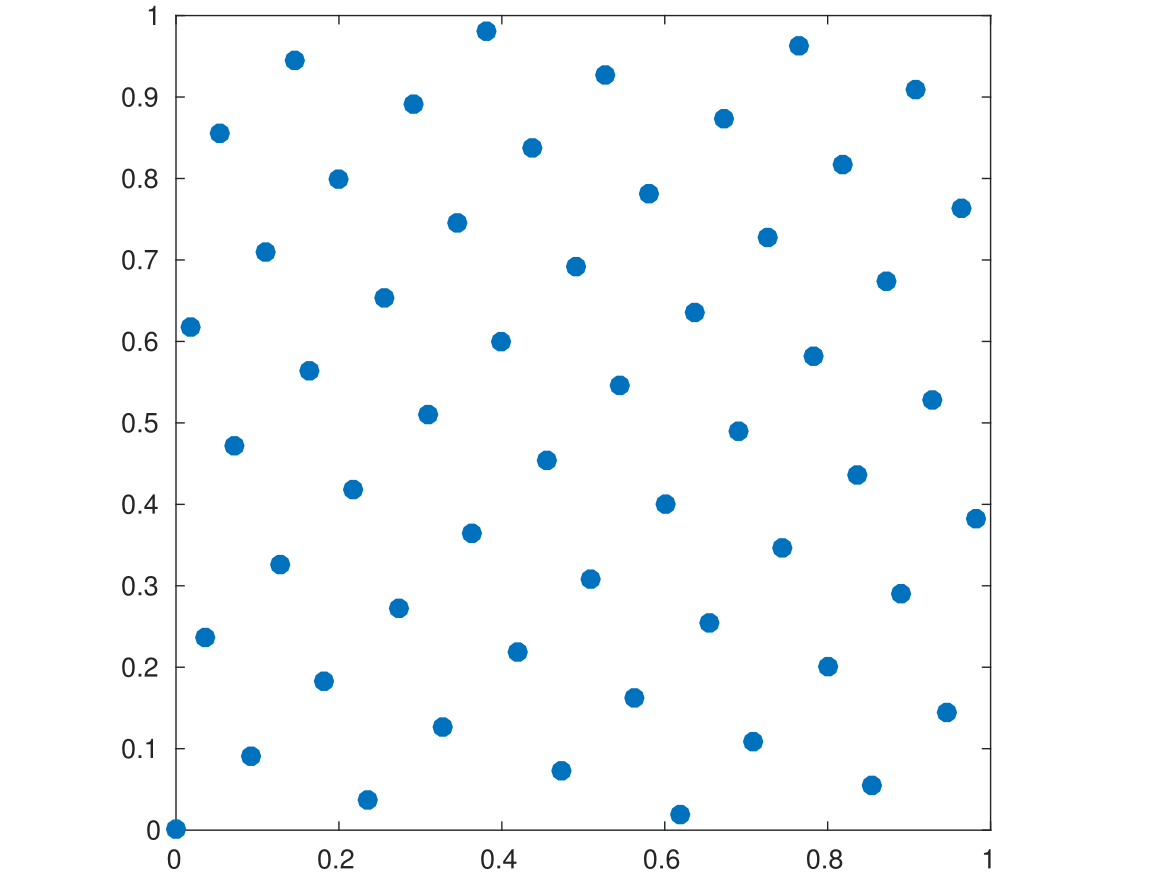
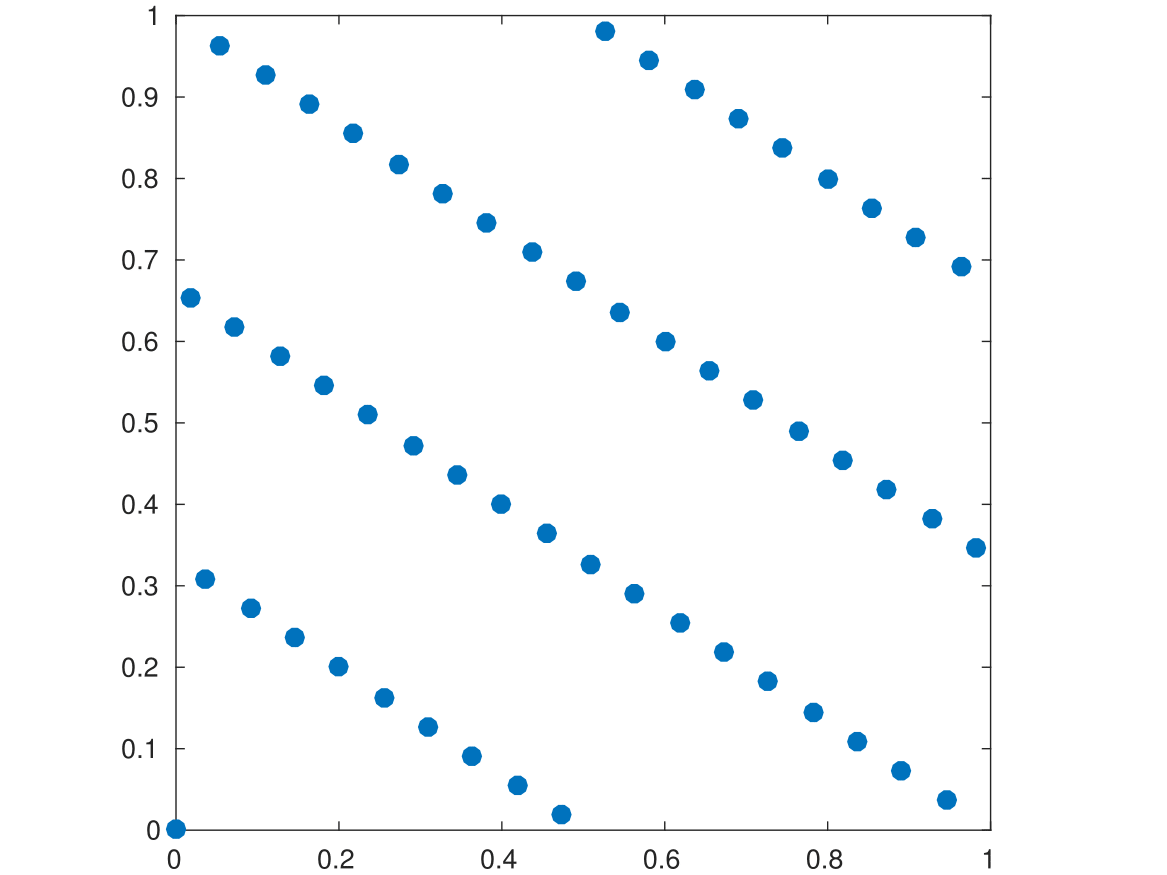
上の図の両方とも格子です。点の数は同じですが生成ベクトルが違います。
$N=55$, $g_1=1$ですが、$g_2$の値が左は$34$、右は$36$です。
生成ベクトルのちょっとした違いが、見て分かるとおり一様性に大きく影響します。
ちなみに、左図のよい格子はフィボナッチ格子と呼ばれる格子です。
一般に$g_1=1$として、$N$と$g_2$を隣り合うフィボナッチ数とすることで、よい格子ができます。
「$g_2/N$の連分数展開にでてくる最大の数」が小さいときよい格子になることが知られています。
隣接するフィボナッチ数はその数が$1$となるペアという仕組みです。
空間の次元$s$が大きいときは、よい格子の構成問題は格子の幾何学の問題に帰着されますが、数学的なよい格子の一般的な構成法ははっきりしていません。かわりに、生成ベクトルの要素を(何らかの基準に従って)貪欲にサーチしていく、いわゆるComponent by Component 法によりよい生成ベクトルを探索することが多いです。Dirk Nuyens先生のページなどに生成ベクトルの情報があります。
デジタルネット
2元体上の$m$次元ベクトル空間$\mathbb{F}_2^{m}$ の元を、$[0,1]$に属する$m$桁$2$進小数と同一視します。
同様に、$sm$次元ベクトル空間 $\mathbb{F}_2^{m \times s}$の元を、$[0,1]^s$に属する$m$桁$2$進小数の組と同一視します。
$P \subset [0,1]^s$がこの同一視を通して$\mathbb{F}_{2}^{m \times s}$ の線形部分空間とみれるとき、$P$をデジタルネットといいます。
この定義だと抽象的すぎるので、ふつうは生成行列とよばれる、$\mathbb{F}_{2}$成分の$m \times m$行列を$s$個決めて、$2^m$種類ある$\mathbb{F}_2^{m}$のベクトルとの積をそれぞれとることで、$s$次元空間内の$2^m$個の点を作り出します。
もちろん、格子の場合と同様に、ちゃんと基底を選ぶことではじめてよいデジタルネットが作れます。
Sobol'列やNiederreiter-Xing列(の最初の$2^m$点)が有名です(上のリンクにこれらもあります)。
MATLABの場合、Statistics and Machine Learning Toolboxを持っていれば、
N=pow2(10); % number of points
s=2; % dimension
P = sobolset(s);
points = net(P,N); % N*s行列として格納
のように、実質2行で実装可能です。ちなみに、上記の点列の構成には、有理式のローラン展開、有理点をたくさんもつ代数曲線、などが活躍します。
高次収束
この節では、$s$変数関数$f$に対し$(\partial x_1 \cdots \partial x_s)^\alpha f$が連続になるとき、$f$が$\alpha$次の滑らかさをもつといいます。
被積分関数$f$が$1$次の滑らかさをもつとき(より一般には全変動有界のとき)、超一様点集合を用いたQMCの積分誤差は$O(N^{-1+\epsilon})$で収束することはすでに紹介しました。実は、格子やデジタルネットのQMCでは、$f$により高い滑らかさを仮定することで、より高速な収束が達成できる場合があります。
格子のQMCの場合
$f$が周期的な$\alpha$次の滑らかさをもつとします。このとき、うまく格子を選べば、 $O(N^{-\alpha+\epsilon})$での収束が達成されます。
証明には以下の事実を用います。
- 事実1: $f$が周期的な$\alpha$次の滑らかさをもつとき、$f$のフーリエ係数は$\alpha$次のオーダーで減衰する。
- 事実2: 格子によるQMCは、多くの三角関数をぴったり積分する。
- 事実3: 事実2において、あらゆる「低周波の三角関数」をぴったり積分するような良い格子が存在する(サーチできる)。
すると、事実3でみつけたよい格子によるQMC積分誤差は、事実2により$f$の「高周波成分」によるQMC積分誤差となりますが、事実1によりその振幅(フーリエ係数)はきわめて小さいので、積分誤差も小さくなるという寸法で証明できます。
デジタルネットのQMCの場合
$f$が$\alpha$次の滑らかさをもつとします(周期性は仮定しません)。このとき、$s\alpha$次元のよいデジタルネットからinterlaceとよばれる操作により作り出される$s$次元のデジタルネットによるQMCにより、$O(N^{-\alpha+\epsilon})$での収束が達成されます。
証明は格子の場合と同様なステップを踏みます。フーリエ展開のかわりにWalsh関数系という、デジタルネットと相性のよい矩形の関数系で展開します。
Q&A
積分したい関数の定義域が全空間、確率密度がある etc.
QMCを使いたい場合には、積分変換で$[0,1]^s$上の一様分布での積分にもっていきましょう。たとえば多変量正規分布での積分の場合、分散共分散行列をコレスキー分解して逐次積分の形にしたあとで、一変数の正規分布の逆関数法で$[0,1]^s$にもっていくことができます。
分散や信頼区間がないと安心できません
randomized QMCという、「QMC点集合の構造を壊さないようなランダムサンプリングをとる」手法があります。たとえば格子則の場合、$[0,1]^s$からランダムにベクトル$v$ をとって格子全体を一斉に$v$だけ平行移動する、ランダムシフトという方法があります。デジタルネットならスクランブルという方法があります。収束オーダーはおおむねQMCと同等以上になります。
で、本当に役に立つの?
実のところ、問題の性質に大きく依存します。役に立つ例としては、オプション価格の計算に現れる360次元の数値積分をQMCでうまく積分できるという報告が1990年代になされて以降、金融工学の分野では積極的にQMCが研究されています。
数値実験例
簡単な例ですが、被積分関数を指数関数 $f(x) = \exp{}(x_1 + \cdots + x_s)$ として、Sobol列と乱数列(1回のみ発生)により、以下のMATLABコードを用いて数値積分してみました。
m=20;% max(log2(number of points))
s=4; % dimension
QMCerr = zeros(1,m);
MCerr = zeros(1,m);
Eval = @(points) mean(exp(sum(points,2))); % integrand = exp(sum(x))
Trueval = (exp(1)-1)^s;
Err = @(points) abs(Eval(points) - Trueval)/Trueval; %relarive integration error
for i = 1:m
N = pow2(i); % Number of points;
%tic
P = sobolset(s); % Get Sobol sequence;
Sobol = net(P,N);
QMCerr(i) = Err(Sobol);
%toc
%tic
Rondom = rand(N,s);
MCerr(i) = Err(Rondom);
%toc
end
III = (1:m);
f1 = figure;
plot(III, log2(QMCerr), III, log2(MCerr), III, -III, III, -1/2*III)
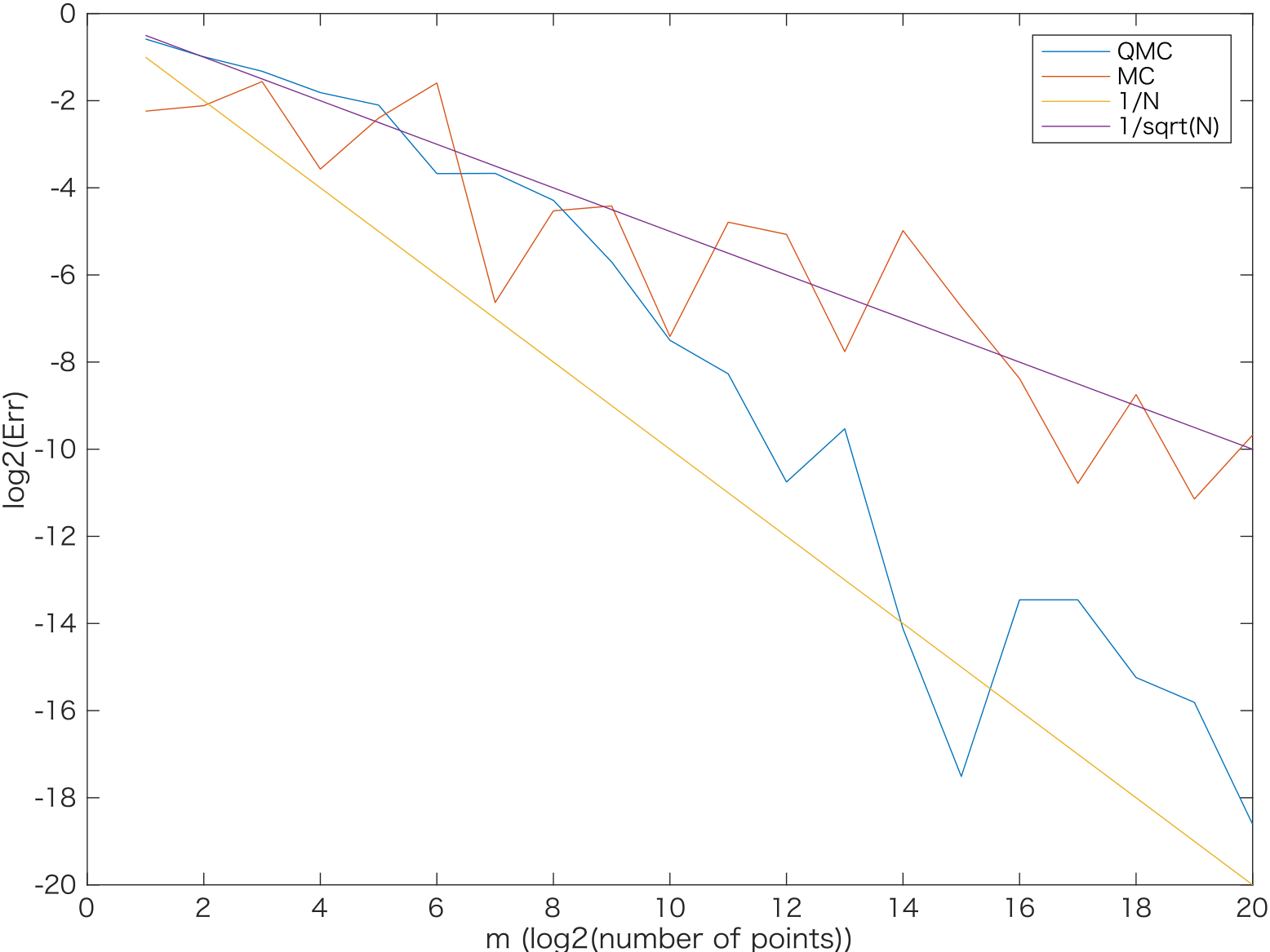
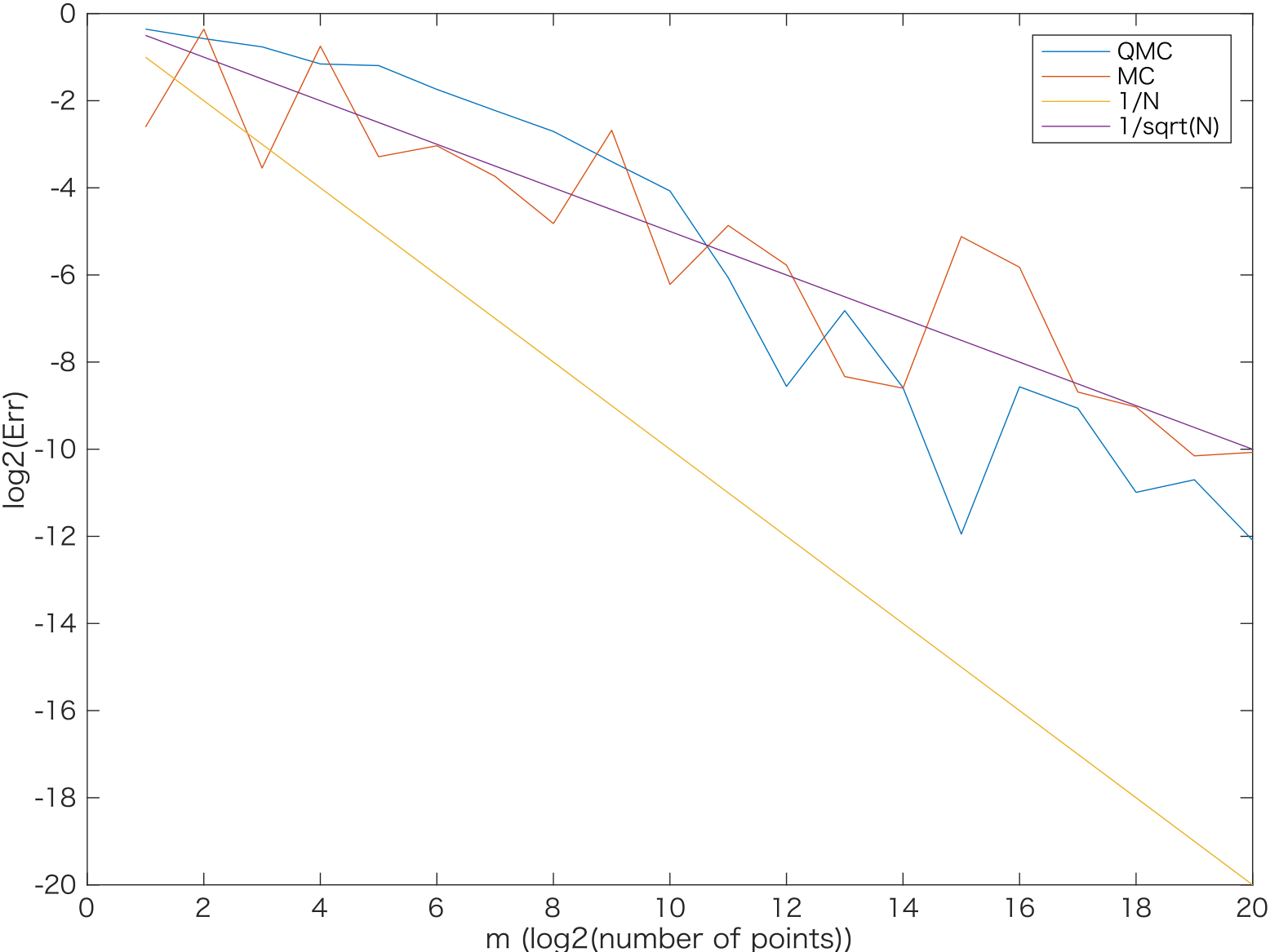
次のグラフで、次元$s$が$2,4,10,20$ の場合に相対誤差をlog-logプロットしました。なお、赤線がモンテカルロ、青線がSobol列によるQMC、黄線が$O(N^{-1})$の収束、紫線が$O(1/\sqrt(N))$の収束をそれぞれあらわします。
!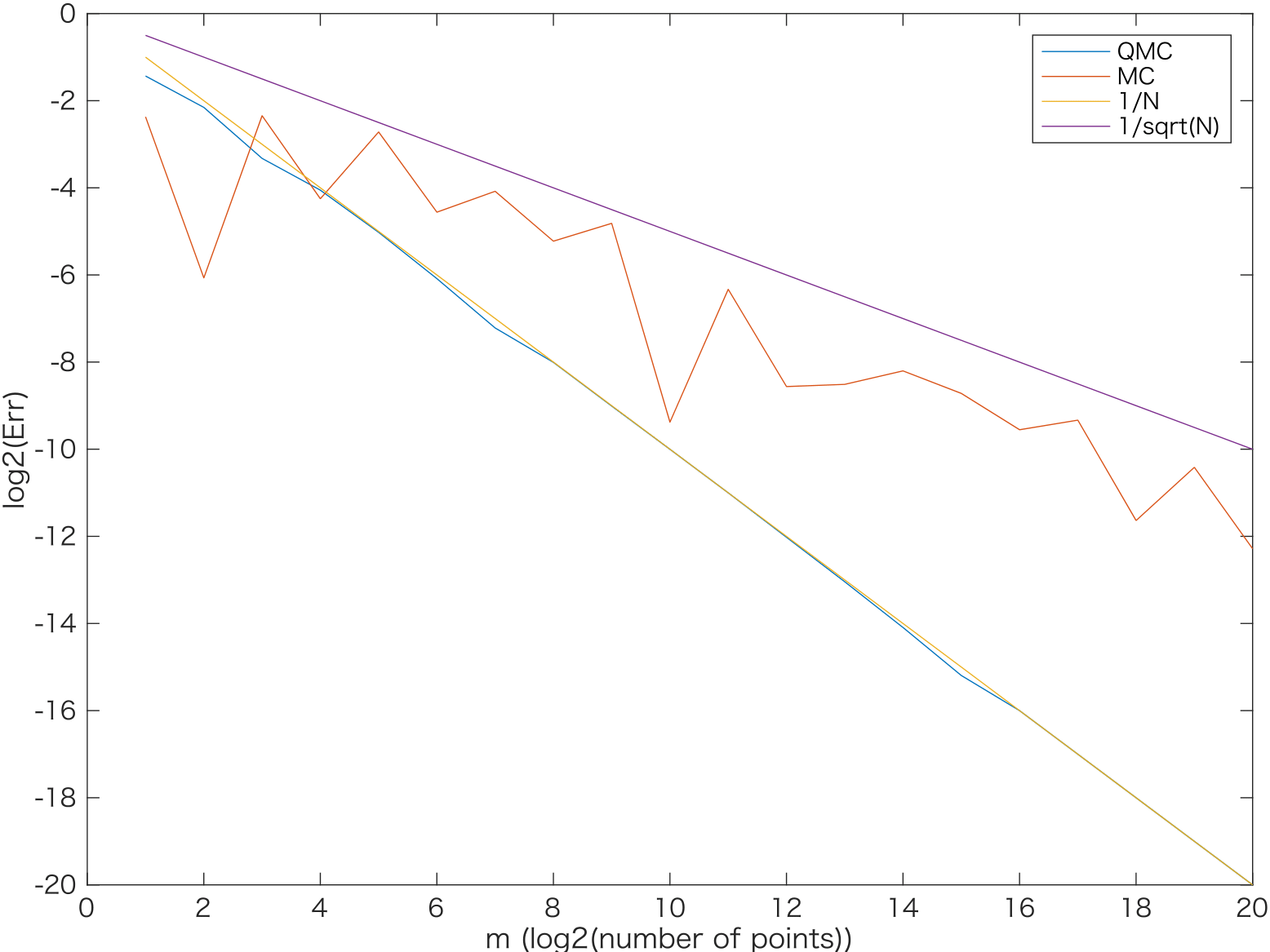 !
!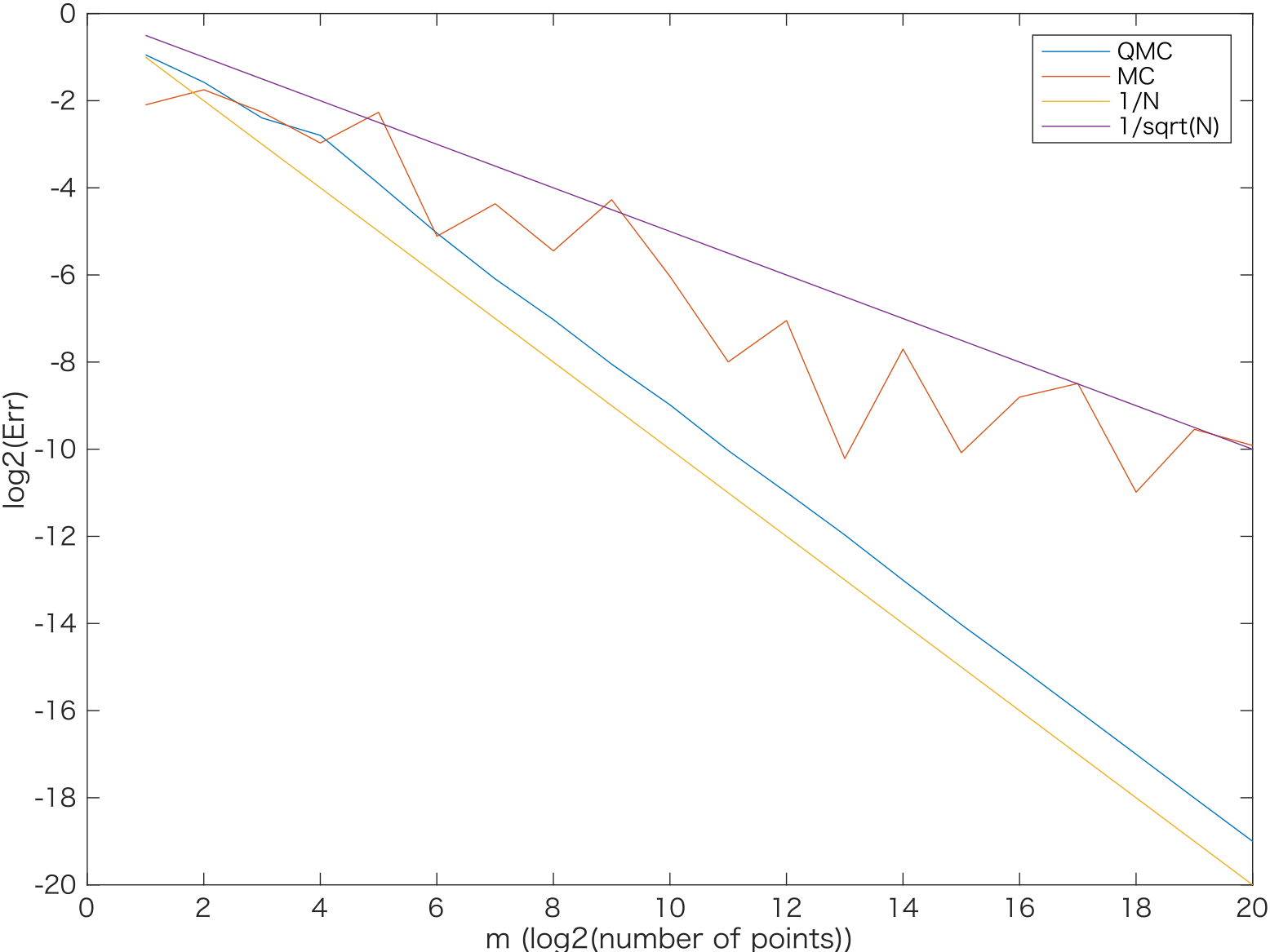
左上が2次元、右上が4次元
左下が10次元、右下が20次元
$s=2,4$のときにはQMCの誤差はきれいに$N^{-1}$に近いオーダーで収束しています。
$s=10$の場合は、$N=2^{10}$点くらいまで待てば$O(N^{-1})$に漸近する収束オーダーが観察できました。
$s=20$になると、$N=2^{20}$点までノードを増やしてもモンテカルロ法と同程度の誤差にとどまりました。
また、上のMATLABコードでtic-tocのコメントアウトをはずして実行時間を計測しました。$s=20$, $N=2^{20}$の場合、QMCでは0.297865 秒、MCでは 0.201823 秒となりました。
参考文献
ディスクレパンシーやデジタルネットに関する基本的文献です。
Harald Niederreiter, "Random Number Generation and Quasi-Monte Carlo Methods", CBMS-NSF Regional Conference Series in Applied Mathematics 63, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1992.
QMCのサーベイ論文です。
Dick, Josef, Frances Y. Kuo, and Ian H. Sloan. "High-dimensional integration: the quasi-Monte Carlo way." Acta Numerica 22, 133-288, 2013.
和書では、以下が挙げられます。
以下の2冊は超一様点列についてページが割かれています。
汪 金芳 (著), 手塚 集 (著), 上田 修功 (著), 田栗 正章 (著), 樺島 祥介 (著), 甘利 俊一 (編集), 竹村 彰通 (編集), 竹内 啓 (編集), 伊庭 幸人(編集) "計算統計 I—確率計算の新しい手法 統計科学のフロンティア 11",
岩波書店, 2003.
における手塚先生の章
手塚 集 (著), 九州大学マス・フォア・インダストリ研究所 (編集), "確率的シミュレーションの基礎", IMIシリーズ: 進化する産業数学, 2018.
格子則については、以下の名著にも詳しい説明があります。
杉原 正顕 (著), 室田 一雄 (著), "数値計算法の数理", 岩波書店, 2003