次のような座標系を考える。
この時、
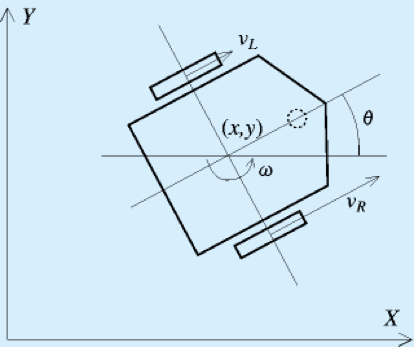
\frac{dx(t)}{dt}=v(t)cosθ(t) \\
\frac{dy(t)}{dt}=v(t)sinθ(t) \\
\frac{dθ(t)}{dt}=ω(t) \\
これを解析的に解く事はできない
ここで、オドメトリ、デッドレコニングと呼ばれる自己位置推定の手法がある。
ここで連続時間系なので、離散時間にするときには、これを用いてシミュレーションする
ここで直線近似と円弧近似が考えられる
直線近似では、Δt秒間直線を移動すると考える
円弧近似では、Δt秒間円弧を移動すると考える
- 直線近似
\frac{x_{t+1}-x_{t}}{Δt}=v_tcosθ_t \\
\frac{y_{t+1}-x_{t}}{Δt}=v_tsinθ_t \\
\frac{θ_{t+1}-θ{t}}{Δt}=ω_t \\
よって、
x_{t+1}=x_t+Δtv_tcosθ_t \\
y_{t+1}=y_t+Δtv_tsinθ_t \\
θ_{t+1}=θ_t+Δtω_t
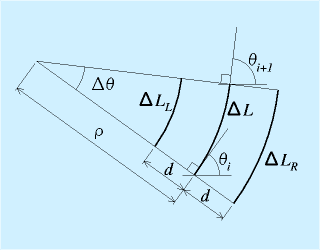
- 円弧近似
移動している時の平均角度は$θ_t+\frac{Δθ}{2}$
よって、ΔxはΔLの直線のcos成分
つまり、
x_{t+1}=x_t+Δx=x_t+ΔLcos(θ_t+\frac{Δθ}{2}) \\
y_{t+1}=y_t+Δx=y_t+ΔLsin(θ_t+\frac{Δθ}{2}) \\
結局直線近似してるね。。。
これでは、$x_t$から$x_{t+1}$までの直線の距離をΔL（弧の長さ）としている
ここで、厳密にこの弧の長さを求めると、
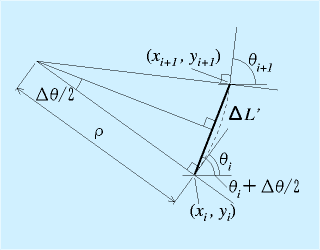
$$ΔL'=2ρsin(\frac{Δθ}{2})$$
代入して、
x_{t+1}=x_t+2ρsin(\frac{Δθ}{2})cos(θ_t+\frac{Δθ}{2}) \\
=x_t+\frac{Δθρsin(\frac{Δθ}{2})cos(θ_t+\frac{Δθ}{2})}{\frac{Δθ}{2}} \\
=x_t+Δθρcos(θ_t+\frac{Δθ}{2})\frac{sin(\frac{Δθ}{2})}{\frac{Δθ}{2}} \\
=x_t+Δθρcos(θ_t+\frac{Δθ}{2})sinc(\frac{Δθ}{2})
sinc(θ)はマクローリン展開すると、
$$sinc(θ)=1+\frac{θ^2}{3!}+\frac{θ^4}{5!}+・・・$$
ここで、１次近似してみると、
x_{t+1}=x_t+Δθρcos(θ_t+\frac{Δθ}{2}) \\
=x_t+ΔLcos(θ_t+\frac{Δθ}{2}) \\
同じ事になる。つまり、円弧を直線に近似する事は、ΔL'を１次近似することに対応する
tracer_kinematics.m
function obj = simu(obj,v,omega)
D_theta=omega*obj.DT;
obj.theta=obj.theta+D_theta;
if omega==0
obj.D_L=v*obj.DT;
DX=obj.D_L*cos(obj.theta);
DY=obj.D_L*sin(obj.theta);
else
r=v/omega;
obj.D_L=2*r*sin(D_theta/2);
DX=obj.D_L*cos(obj.theta+D_theta/2);
DY=obj.D_L*sin(obj.theta+D_theta/2);
end
obj.x=obj.x+DX;
obj.y=obj.y+DY;
end
加速度と角加速度まで考慮すると
tracer_kinematics.m
function obj = simu2(obj,a,alpha)
obj.v=a*obj.DT;
obj.omega=alpha*obj.DT;
D_theta=obj.omega*obj.DT;
obj.theta=obj.theta+D_theta;
if obj.omega==0
obj.D_L=obj.v*obj.DT;
DX=obj.D_L*cos(obj.theta);
DY=obj.D_L*sin(obj.theta);
else
r=obj.v/obj.omega;
obj.D_L=2*r*sin(D_theta/2);
DX=obj.D_L*cos(obj.theta+D_theta/2);
DY=obj.D_L*sin(obj.theta+D_theta/2);
end
obj.x=obj.x+DX;
obj.y=obj.y+DY;
end
この時、作用反作用の法則により、モータには慣性力が働く