HTTF2022予選の6.376M(1位)解法+経緯

Hack to the Future Contest 2022 の予選に参加し，6,376,124点(1ケース平均2125.37点)で1位でした．

暫定テストの点数は最高で105,661点(最終提出は105.5k台)でした．

問題の概要

詳しくは公式を参照．

• 1000個のタスクを20人にうまく割り振って最短時間で処理させる
• タスクの依存関係はDAGになっていて，依存しているタスクが全て終わるまで始められない
• タスクの難易度が10~20次元のベクトルとしてわかっていて，各人間にも同じ次元のスキルベクトルが付与されているが，人間のスキルベクトルは情報として与えられない
• 人間がタスクをやる時，人間のスキルベクトルの中にタスクの難易度ベクトルに足りない成分があると，足りていない分だけタスクをやるのに時間がかかる．
• 各タスクにかかった時間が(誤差付きで)わかるので，人間のスキルベクトルを推定しながらうまい感じにタスクを配分したい

最終解法

• 推定パートと最適化パートに分ける．
• 推定パートはMCMC(の一種のギブスサンプリング)を使った．(詳しいモデルは後述)
  • 「スキルベクトルの1つの成分を動かす」遷移と「スキルベクトルの2つの成分を，和を保ちながら動かす」遷移を作り，ランダムに織り交ぜた．
• 最適化パートは，まだ処理されていないタスクたちのうち手前の部分だけ最適化し，残りの部分は適当な評価関数を作るのに使う
  • 評価関数は，「最適化しない部分は無限人で処理できると仮定した時に全てのタスクが終わるまでの時間」的なものであるが，maxをlogsumexp関数に置き替えたものを使う．(詳しくは後述)
  • logsumexp関数のうまい性質(logsumexpと+で半環になっていること)を使うと，最適化しない部分は各ターン一度だけ動的計画法で前処理することで，評価関数が改善したかどうかをそこそこ高速に判定することができる．
  • 最適化するタスク全てを「そのタスクに間接的に依存するタスクを無限人で終わらせるのにかかる時間」的な数値が大きい順に並べ替え，その順番で貪欲に最適な(人, 時間区間)を割り振っていった状態を初期解とした．(この初期解をそのまま出すと103.6kくらいになる)
  • そこから山登り法で適当に最適化したものを出して，105.6k

推定パート

今回の問題は，各人間について独立に推定でき，パラメタの次元数が10~20とかなり少ない一方，綺麗なモデル(e.g. 指数型分布属)で近似することができなさそうので，何も考えずにMCMCを使った．

問題のモデルをそのまま使うと，尤度が0になるようなパラメタが出てきてしまって嫌なので，観測誤差を±3の一様乱数の代わりに標準偏差3/√3の正規分布で近似した．すなわち，所要時間を$t_{i,j}$，難易度を$d_{i,k}$,取り組んだ人のスキルを$s_{j,k}$として
$$t_{i,j}=\sum_{k=1}^{K} \max(0, d_{i,k}-s_{j,k}) + r'_{i},\qquad r'_{i} \sim \mathcal N(0, 3^2/3)$$

とした($\mathcal N(\mu, \Sigma)$で平均$\mu$, 分散$\Sigma$の正規分布を表す)．

スキルベクトルの事前分布$P(\vec{s}_j)$は，入力の生成方法からしてK次元超球の半径$|\vec{s}_j|$での表面積に反比例するはずなので，$P(s_{1...K}) \propto |\vec{s}_{j}|^{-(K-1)} (20\le |\vec{s}_{j}| \le 60)$とする．

これでモデルが立ったので，どうやってMCMCで遷移させるかを考える．最初にやったのは，スキルベクトルの一つの成分k以外を固定して，成分kのみを動かすという遷移である．具体的には，$1...N_j$のタスクを人間$j$がやったものとすれば，成分$k$以外を固定した条件付き分布
$$\begin{align}s_{j,k} &\sim P(s_{j,k}\mid t_{1...N_j,j}, s_{j,1...K\backslash{k}}) \\
&= \frac{P(s_{j,k}, t_{1...N_j,j} \mid s_{j,1...K\backslash{k}})}{P(t_{1...N_j,j} \mid s_{j,1...K\backslash{k}})}\\
&= \frac{P(s_{j,k} \mid s_{j,{1...K}\backslash{k}})P(t_{1...N_j,j} \mid s_{j,1...K})}{P(t_{1...N_j,j} \mid s_{j,{1...K}\backslash{k}})}\\
&= \frac{P(s_{j,1...K})\prod_{i=1}^{N_j}P(t_{i,j} \mid s_{j,1...K})}{P(s_{j,{1...K}\backslash{k}})P(t_{1...N_j,j} \mid s_{j,{1...K}\backslash{k}})}\\
&\propto P(s_{j,1...K}) \prod_{i=1}^{N_j} P(t_{i,j} \mid s_{j,1...K})\end{align}$$

($1...K\backslash k$は，$1...K$から$k$を除いたものを表す)からサンプリングすることを繰り返すと，サンプルされる$\vec{s}_j$の分布はスキルの事後分布$P(s_{j,k'=1...K}\mid t_{i=1...N_j,j})$に収束していく．それぞれのサンプルされた$\vec s_j$について$t_{i,j}$を計算し，その期待値と分散をとって，その情報を下流の最適化パートで使う．

$P(t_{i,j} \mid s_{j,k'=1...K})$の方は$s_{j,k}$に関して区分的にガウス関数になっているが，$P(s_{j,{1...K}})$という変な形の事前分布がくっついてしまっているために右辺は全体として綺麗な関数ではない．それでも，今回は$s_{j,k}$は整数なので，取りうる値は0～60の61通りしかなく，それら全てに関して右辺の値を求めることでサンプリングした．

この確率分布の計算を高速化するために，右辺の確率のlogをまず計算して最後にexpを取って正規化した．$P(t_{i,j} \mid s_{j,k'=1...K})$が区分的にガウス関数なので，$\log P(t_{i,j} \mid s_{j,k'=1...K})$は区分的な二次関数であり，よくある累積和のテクニックを使うことで$O(S_{max}N_j)$から$O(S_{max}+N_j)$の計算量に落とすことができる．($S_{max}$はスキルの成分の最大値とする．今回は60．)

最初はこの遷移だけでやっていたが，ビジュアライザに表示してみるとプルプルしていてあんまり効率的に探索してくれなさそうということがわかった．そこで，もう一つの遷移として，スキルベクトルの2つの成分$k_1, k_2$を選んで，それら以外の成分の値と，$k_1$成分+$k_2$成分の値を固定して動かすというものも考えた．一つの値を動かす場合と似たように考えることができ，同じように累積和を使って計算を高速化できる．この遷移を入れることによって，ちょっとは動きがマシになり，推定精度が少し上がった．

最適化パート

準備: クリティカルパス解析的なもの

まず，準備として，大雑把に各タスクがどのくらい急いでやる必要があるのかを把握する必要がある．これを20人しかいないという制約を込めて実際に計算するのは大変なので，代わりに，仮に無限人で並列処理できた場合にどのくらい律速となるか(=クリティカルパス解析)を考えることとした．

概念的には，各タスクの処理時間(ここでは常に最もそのタスクが得意な人が処理することとする)を$t_i$として，依存関係のDAGを$G$とすると，無限人で処理した時にかかる処理時間$T$は
$$T = \max_{\tau\in \mathrm{path}(G)} \sum_{i=1}^{|\tau|}t_{\tau_i}$$

と簡潔に書くことができる．ただし，$\mathrm{path}(G)$は$G$上の全てのパスの集合であり，$\tau_i$はパス$\tau$の$i$番目のタスクを表すこととする．

しかし，これを評価関数として使うには2つの問題がある．

1. 実際には$T_i$は推定値であり，揺らぎがあるので律速のパスではない部分も「なるだけ早めに終わらせる」ということにメリットがあるはずだが，この評価関数の値は律速となるパス以外は改善しても変わらない．
2. 実際には同時に作業できるのが20人であり，有能な人はもっと限られるので，たくさんのタスクに依存しているタスクは少数のタスクに依存しているタスクよりも始められるまでの時間が長い可能性が高いが，この評価関数ではそれを考えられない．

そこで，maxの代わりに，次のようなlogsumexp関数を使うことにした．
$$\mathrm{logsumexp}(a_1,a_2,...,a_n) = \kappa\log\left(\sum_{i=1}^n e^{a_i/\kappa}\right)$$

これは，次のグラフのような関数である．(グラフは$\kappa$を0...5まで変化させた時の$\mathrm{logsumexp}(0, x)$を示している)

$\mathrm{logsumexp}$は，$\kappa\to 0$の極限で$\max$に収束していくことがわかる．実際は$\kappa = 25$くらいが一番うまくいったのでそれを使って，
$$T = \underset{\tau \in \mathrm{path}(G)} {\mathrm{logsumexp}} \sum_{i=1}^{|\tau|}t_{\tau_i}$$

というような値(「ソフトな所要時間」的な値)を考えた．(細かいところだが，実際には$t_{i}$は
$$t_i = \min_j\mathbb E_n[t_{i,j}]+\gamma_1\sqrt{\mathbb V_n[t_{i,j}]}$$

として，少し安全よりに見積もることにした¹．ここで，$\mathbb E_n$と$\mathbb V_n$はMCMCでサンプルした標本平均と標本分散である．$\gamma_1$は0.5がうまくいった．)

$\mathrm{logsumexp}$関数は，$\max$と同じように次のような素敵な恒等式が成り立つことが簡単にわかる．

• 交換則 $\mathrm{logsumexp}(a,b) = \mathrm{logsumexp}(b,a)$
• 結合則 $\begin{align}\mathrm{logsumexp}(a,\mathrm{logsumexp}(b,c)) &= \mathrm{logsumexp}(\mathrm{logsumexp}(a,b),c) \\&(= \mathrm{logsumexp}(a,b,c))\end{align}$
• +との分配則 $\mathrm{logsumexp}(a,b) + c = \mathrm{logsumexp}(a+c, b+c)$

これは，$\mathrm{logsumexp}$を加法，$+$を乗法,$-\infty$と$0$を加法と乗法の単位元とした時に半環になっている，と言うこともできる．これらの恒等式を使うと，上で定義した$T$を計算する漸化式を立てることができる．(クリティカルパス解析と同じことができる．)

この漸化式の立て方は「前から計算する方法」と「後ろから計算する方法」の2通りあって，今回のアルゴリズムでは両方を使う．

「前から計算する方法」では，$A^i$を「タスク$i$を始められる最速の時間」，$B^i$を「タスク$i$を終わらせられる最速の時間」として，動的計画法を回せば良い．

$$\begin{align}A^i &= \underset{j: (j, i)\in E(G)}{\mathrm{logsumexp}} \space B^j\\
B^i & = A^i + t_i\end{align}$$

初期条件は，何にも依存していないタスク$i$について$A^i=0$と考える．$T$の値は，何からも依存されていないタスク$j$全てについて，$B^j$のlogsumexpを取ると求められる．

一方，「後ろから計算する方法」では，$B_i$を「タスク$i$が終わってから全タスクが終わるまでにかかる最短の時間」，$A_i$を「タスク$i$が始まってから全タスクが終わるまでにかかる最短の時間」として，動的計画法を回す．

$$\begin{align} B_i &= \underset{j: (i, j) \in E(G)} {\mathrm{logsumexp}}\space A_i\\
A_i &= B_i + t_i\end{align}$$

さっきとは反対に，初期条件は何からも依存されいないタスク$i$について$B_i = 0$とし，$T$は何にも依存していないタスク$j$全てについて$A_j$のlogsumexpを取ると求められる．

最適化をするタスクの選択と，最適化の評価関数

まず，$A^i$がある閾値未満のタスクだけを集めて，それを最適化の対象とする．集めたタスクの集合を$S$，そうでない未完のタスクの集合を$\bar S$と書く． (閾値は，15がうまくいった．)

$G$から$S$内の頂点同士をつなぐ辺を除いたグラフを$\bar G$とする．この上で$A_i, B_i$を計算し，それを$\bar A_i, \bar B_i$と書くことにする．

$S$内のタスクについては，「誰がどの順番でやるか」を最適化する．誰がどの順番でやるか決まれば，$S$内のタスク同士の間の依存関係を考えれば，$S$内の各タスクがいつ実行されるかがわかる．(ここでは誰がやるのか決まっていて不確定性が少ないのでlogsumexpではなく普通にmaxを使う．　これによって計算された各タスクの始まりと終わりの時間を$\tilde A^i, \tilde B^i$と書くことにする．)

評価関数$T'$を，
$$T' = \underset{i\in S}{\mathrm{logsumexp}} \space (\tilde B^i + \bar B_i)$$

で作り，これを$S$内のタスクの人員配置と順番を並べ替えることで最小にすることを目指した．(気持ち的には，人員配置がはっきり決まっている部分は所要時間を正確に計算して，はっきり決まっていない部分は無限人いると仮定してlogsumexpでソフトに計算することにした時の$G$全体の所要時間のようなものである．)

この評価関数は，$S$内の人員配置と順番を部分的に変更した時に，$S$内で変更した部分に依存するタスクのみについて再計算をすると，(logsumexpは単調増加だから)全体の評価関数が増えるのか減るのかが分かって，計算時間を短縮できる．

初期解

今回は最適化にかけられる時間が1ターンあたり大体3msとかなり短いので，良い初期解をとることが重要となる．ここでは次のようにとった．

• $S$内のタスクを，$A_i$が長い順に並べ替える．
• タスクを最も早い時間に終わらせられる衝突しない(人,時間区間)を貪欲に配置していく．

実は最初は最適化せずにこれだけでなんとかならないか頑張っていた．これだけでも103.6kくらいには到達したが，頭打ちになった．

山登り法

最適化とは言っても3msしかない上に一回の評価関数の評価がそこまで軽くなくて回数が稼げないので，焼き鈍しとかではなくて単純な山登り法で適当にやった．また，最適化してもそのターンで結果を使わないとやり直しになって悲しいので，そのターンで使う結果に直接影響を与える遷移のみに絞った．

作った遷移は次の3通り．

• ある作業中ではない人間を選び，その人が他の誰かに割り当てられているタスクを奪う
• ある作業中ではない人間を選び，その人の一番最初のタスクを誰かに押し付ける
• ある作業中ではない人間を選び，その人の一番最初のタスクと他の誰かのタスクを交換する
  可能な遷移を全て1度ずつ試し，評価関数が改善するならそれをその遷移を実行するということを繰り返した．全て試すのではなく確率的に遷移を試すのもやってみたが，計算時間あたりの効果が全部一度ずつ試すよりも薄かったのでやめた．

計算上の細かい工夫

ベンチマークをとってみると，かなりの部分の計算時間をlogsumexpを計算するためだけに使っていることがわかった．そこで，logをとってまたexpを取ることを可能な限り少なくするため，expの状態で評価関数が改善したかどうかを計算することにした．

オーバーフローしないか心配だったが，$\tau=25$で日数が高々2000日であることを考えると$e^{80}$くらいまでの値を扱えればよくて，doubleに余裕で入る．この工夫で，最適化パートの計算時間がかなり短くなった．

その他の細かい諸々

• 時間管理．最後の方はMCMCがあまり意味がないので，3秒中2.6秒を超えたら推定値を更新するのをやめた．それでも最適化の方でそこそこ時間がかかるので，下手をするとTLEになることがあり，2.95秒を超えてからは最適化せずに貪欲法の初期解のまま突っ込むようにした．実際はシステスでは2.95秒を超えたケースはなかったので，良かった．
• 力試し期間．最初から上の方法で推定+最適化すると，あまり情報がないうちは下手な人に難しいタスクを振ってしまうことが大量発生して，効率が悪くなることがある．そのため，Rの値に応じた力試し期間を設けて，その間は
  $$\mathbb E_n[t_{i,j}]-\gamma_2\sqrt{\mathbb V_n[t_{i,j}]}$$
  の値が小さい(人,タスク)のペアから貪欲にタスクを割り振っていくことにした．先ほどの$t_i$の計算と似た式であるが，+と-が逆になっていることに注意．目的が推定精度を高めることなので，どのくらいうまくできるかわからないようなタスクから優先的に試すことにした．力試し期間の長さは，$R<1800$では150日，$1800\le R < 2200$では50日，$2200 \le R$では0日(いきなり最適化を始める)にした．最適化をしていなかった頃はこれでかなり伸びたのでずっと入れていたが，コンテストが終わってからこれを抜いてみても平均0.5点しか下がらなかったので，多分本質的ではない．

結果

注: ここで示しているデータは，時間制限なしで回した時のデータです．

• 手元で5000ケース回した時の平均点: 2129.8456 ± 2.7950点 (標準偏差は平均点の推定標準偏差です．)
• seed5

seed5の場合はこうなりました #HTTF pic.twitter.com/PSHEkJyQi1

— いんたく (@contramundum2) November 13, 2021

• seed0　(注: これは最終版とちょっとパラメタが違って，コンテスト中に共有したseed0と同じ．最終版ではこれより点数が下がって，2216点でした．)

MCMCの推定を表示させたseed0の動画です。(本当はこのサンプリングを情報が更新されるたびに70回やって、まだやっていない全タスクについてのかかる時間の平均と分散を取るので、この色よりは推定精度が良いはず) pic.twitter.com/X3OYjKZ5hP

— いんたく (@contramundum2) November 13, 2021

* (R, K)ごとの得点分布 * seed0のタスク処理時間の推定値の平均二乗誤差の平方根: 4.098程度

やりたかったけどできなかったこと，やったけど伸びなかったこと

• より正しい推定．　誤差を正規分布で近似するのではなく， より正しいモデル(決められた範囲の一様乱数)に近いものを使うと良くなりそうな気がして，やってみたが，なぜかあんまりうまくいかなかった．理論的には無限に時間をかければうまくいくはずなのだが，現実的な時間でギブスサンプリングがどのくらいうまくいくかは，作った遷移でどのくらい素早くサンプルを拡散させられるかに依存している．正規分布モデルの方がその点で良かったのかもしれない．
• より賢い最適化． 計算時間がかかってしまって，単純な山登り法を超える方法を実装できなかった．本当は局所解から抜け出せる方法を使った方が良いのかもしれない．また，最適化は毎ターン貪欲法の初期値から始めたが，そうではなく一つ前のターンで最適化した結果と貪欲法の結果を比べて良い方を初期解にするともっとよくなったかも．しかしこれも実装が大変で間に合わなかった．
• より賢い$t_i$の計算． 本来，$t_i$は「今は推定誤差があるけど，将来推定が良くなったらより適切に正しい人を選べる」ということを考慮して計算するべきである．実際，上の式ではなく，確率変数$T_i := \min_{j} t_{i,j}$の$\alpha$分位点をを取る，というような方法を試してみた．詳しくは省略するが，$t_{i,j}$を正規分布だと思えば，$\alpha$分位点の値は累積分布関数のlogにニュートン法を適用して求めることができる(正規分布の累積分布関数のlogが上に凸になるので，ニュートン法は常に唯一解に収束することがわかる)．これで手元の5000ケースのテストでは平均で1~2点くらい上がったが，計算時間がかかるようになっていて，時間制限がかかって点数が下がることが心配だったので最終提出には載せなかった． (あるいは，サンプリング時に$T_i$の値の履歴を全部保存して，その$\alpha$分位点を持つみたいな考え方もあるかもしれない．しかし，$\alpha$があんまり小さく取れなさそうなのと，サンプリングという計算量の律速パートに$O(\log M)$の計算を増やしてしまうことに気が乗らなかった．)

経緯

注: 今回の開発は途中バグが発覚して手戻りが発生したりなどかなりごちゃごちゃしていて，物語として伝わる形にするために時系列を結構並べ替えています．

序盤 (Day 3-4)

私が問題を見たのは3日目．修論が忙しかったので，問題が面白そうだった場合のみ，週末のみ参戦する，と自分に言い聞かせてから問題を読んだ．このページの長さがその結末を物語っている．(なお修論)

何をすればいいか，はじめの方は全然わからなかった．最適化をしないと勝てなさそうに見えるけど，いつもと違って今回は3秒で1000回くらい最適化しないといけない．推定パートは置いといて，最適化パートだけを取り出すと実世界でよくありそうな問題だな，と思って，記憶を頑張って辿って思い出したのは，生産管理の授業で習ったアローダイアグラムと，同じ先生が言ってた「ガントチャートの最適化は一般には難しい」という言葉だけだった．

情報が不確定なのだから，最初から最後まで最適化するのは制限時間3秒でやることとしては明らかに得策ではない．こういうような問題において，制御工学とかでよくやるのは，「現在時刻から未来nステップだけを考えて最適化し，その結果の1ステップ目だけを使う」という考え方である²．しかし，例えば現在時刻から20日間分を最適化するとして，何を最適化すればいいのか? 20日間で終わらせられるタスクの数? いや，そうとは限らないだろう．簡単なタスクはいつでもでき，難しいタスクは今すぐにやらないと依存関係で後で詰まってしまうかもしれない．

アローダイアグラムの話を思い出していたので，クリティカルパス解析をして一番律速になってそうなところを攻めないといけないんだな，というのは思いついた．しかし，クリティカルパス解析はO(N)の計算時間がかかり，これは毎ターンに1回実行するだけなら十分な速度でも，3秒で1000回回る最適化の目的関数とするには遅い．それに，20日分を真面目に決めて残りを無限人で並列処理した時の時間で置き換えるなんてことが正当なのか，わからなかった．とりあえず人々に難しいタスクばっかり押し付けておいて，簡単なタスクは20日後に大量に並列実行するのが最適にならないのだろうか?

でもとりあえず答えはこういう方向にありそうだな，と思って，実装を始めた．まず最初に，とりあえず推定パートはいつか実装しないといけないし実装するか，と思った．

今回の推定パートは，前回推定系の問題が出たAHC003とは違って，正規分布でうまく近似できたりはしない．とりあえずK=3の場合である観測が得られたときにあり得るスキルベクトルの領域を3次元のグラフで描いてみると，直方体の辺と頂点を斜めに切り落として，さらにその厚さ7の表面だけ取り出したみたいな形をしている．複数回観測されると，可能なスキルベクトルの領域は，この形を複数個ずらして重ね合わせた時の共通部分にどんどん絞られていく．一瞬包除原理で共通部分の重心をいい感じに求められるのでは？と考えてはみたものの，観測の数が増えていくにつれて計算量が指数的に増えていってすぐに手に負えなくなることは目に見えていた．何も賢いことはできなかったので，そういう「野生の推定問題」一般に対して通用する最終手段であるところのMCMCに脳死で頼ることにした．

前回実装したというのもあって，今回の実装はそこそこ楽にできた．途中区分二次関数の和を累積和で表して計算を高速化するところはややこしくてバグらせてしまったが，バグが治ればそこそこまともな値が返ってきているな，ということがビジュアライザでわかった．(最初からビジュアライザが有能なのはありがたい．)

推定ができたら，最初に試したのはとりあえず(できるタスク，暇な人)の組で最も素早くできそうなものからやっていく貪欲法だった．もちろん点数は出なかった．次にクリティカルパス分析を実装し，最もその後に依存されているタスクの処理時間が長いようなタスクから順に，貪欲にその時点で空いている最適な人間を割り当てることにした．結果は93224点だった．(その前に一度バグらせて最頻値より低い74708点を出してしまった．)

ビジュアライザーをよくみると，今暇でない人が候補から外されているせいで，結局ただ暇になった人に一番律速になっているタスクを食わせているだけになっているのに気づいた．本当は，今暇になっていなくても，暇になってからあるタスクをやったほうが今暇になっている人にやらせるより早い場合は，その人にやらせた方が良い．これを実装して100382点(この時点では多数のバグが存在していて，この点数は信用ならない)．

中盤1 (Day 4-8)

ここからパラメタ調整ゲーになりそうな機運だったので，公式ジェネレーターを改造して全(R,K)について一つづつ入力を生成した後，ランダムに5000ケースサンプルし，リアルタイムでR,Kと得点の関係をプロットするテストスクリプトを書いた．大体はAHC003とかからのコピペだったが，こういうインフラ系の作業には未だ慣れず，パイプを繋ぐ時のバッファリングとかで苦しめられた．プロットできた時には，RだけじゃなくてKの値によっても自分の解法の点数が大きく変わっていることに気づき，かなり驚いた．

この後は小さな改善とバグの修正の繰り返しで，あんまり書く気が起きない．何かを試してみてうまくいかなくて，色々考えたが結局原因は実装のバグにあって直したら伸びた，の繰り返しだった．

• すでに始めてあるタスクが予測した日を過ぎても終わっていない場合，マイナスの日にタスクを割り振ることができるようになってしまっていたのを修正したら，1k弱くらい?上がった．
• MCMCで平均だけじゃなくて分散を使うべきだな，と思って入れてみたが，全然よくならずに謎だった．しかしある時sqrt(二乗の平均-平均の二乗)で計算していた標準偏差が数値誤差でnanを返していることに気づき，それを直したらちゃんとパラメタ調整次第で点数が上がるようになった．(多分ここまでで101.5k)
• 上述の「力試し期間」を入れてみても最初は点数が下がってしまった．しかし，得点とRの関係をプロットした図を見てみると，明らかにRが小さい時は上がっていて，Rが大きいときに点数が大きく下がっているような挙動だった．(下の画像で，薄い方が最終解法+力試し期間なし，濃い方が最終解法+力試し期間あり)
  
  
  
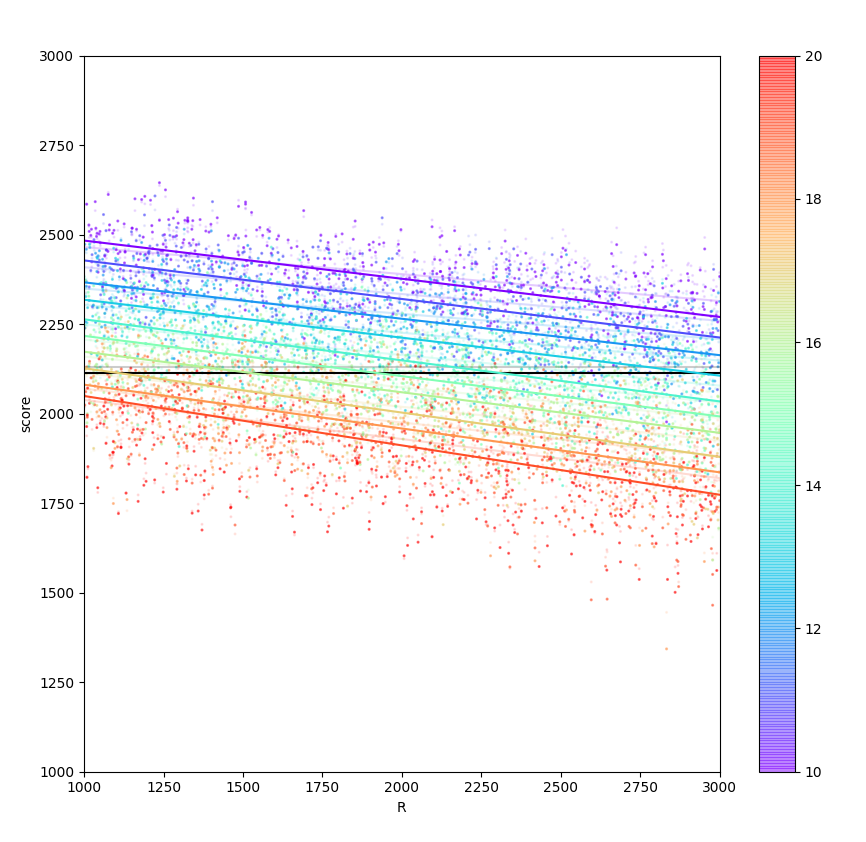
  そこで，Rの値によって場合分けし，Rが小さい時に力試し期間を入れるようにしたらかなり点数が上がった．(102.5k)

この辺で一時期暫定1位になって，*邪悪な目標賞金狙い*が発生し，最初に「週末だけ参戦する」と自分で決めたのを破ることになってしまった．

• ここまでは今すぐ実行できるタスクのみを考えていたが，それだと「後1日で律速のタスクができるようになってそれに最適な人材が今空いているのに，今できる別のタスクを投げてしまう」といったことが起きる．今すぐできなくてもそろそろ実行できるようになる($A^i$の値が小さい)タスクについても考慮に入れた上で，貪欲に(人間,時間区間)を割り当てていく方式をやった．これも最初やってみて全然点数上がらなくて諦めていたが，それぞれの人の暇な日の区間を管理するデータ構造を取り出して試してみたところ3つくらいバグが入ってて，そりゃよくならないわとなった．直したらかなり点数が上がった．ユニットテスト大事．(103k+αくらい)
• 推定にかける時間を増やしたら，ちょっとだけ点数が上がった(+100点くらい)．

一方で時間をかけたが点数が上がらなかったものもあった．上述の「より正しい推定」に書いた部分がこれだった．正規分布を使う理由は特にないはずなのでもっと正しそうな分布を使うと改善する気がして，一様分布に，裾が0なのが嫌なので裾に指数分布を付け加えた分布を考え，それを正規分布の代わりにMCMCに突っ込んでみた．しかし，全然点数がよくならない．推定精度も(推定ができていなくてぶっ飛んだ値を返してくる，という感じではなく，正しく動いていそうな雰囲気を出しているものの)正規分布の場合と比べて誤差が大きい．この結果にはかなりびっくりして，最初は実装のバグを疑ったりしたが，そのようなものは見つからなかった．結局裾確率が指数分布なのが悪いのかな...と言って理解と改善を諦めた．

中盤2 (Day 7-10)

コンテストのこの時期の暫定1~4位くらいは，ひたすら102k~103k台の開発競争を繰り返す闇のゲームと化していて，辛かった．改善量もこれまでは500点とか1000点の改善だったものが100点単位の改善になってきて，これは104kに到達しないのかな...と思い始めていた．

ずっと逃げ続けているの辛い．2位のiehnさんがすごい勢いで迫ってくる．#HTTF pic.twitter.com/2SUuc8dhu5

— いんたく (@contramundum2) November 10, 2021

しかし，突如ValGrowthさんが1位に浮上し，その後iehnさんが104kを叩き出した．この調子だともう一つか二つくらい本質的な改善ブレイクスルーがないと勝てそうにない，と焦って，色々考えた．

最適化がしたい．推定パートはMCMCしかやってないし，最適化パートはまだほぼ自明な貪欲しかやってない．MCMCなんてのは焼き鈍し法と同じく他に賢い方法がない場合の最終手段なわけで，もっと賢い方法がある場合はそっちの方が計算量も推定分散も少ない．それに，おそらく今回の問題では推定パートはそこまで本質ではなく，やっぱり本質は最適化パートなのだろう．そんなコンテストでただのMCMC+貪欲法で賞金を狙おうだなんて，傲慢以外の何者でもない．

では，なぜ最適化ができないか．

評価関数の計算が重いから．そもそも評価関数として何を取ればいいかわかってないから．

温かみのあるお手製の評価関数で戦うという方法は確かにあるが，それは私が得意なことではないし好きなことでもない．5000ケース取って評価してもなお全然5000ケースの取り方によって平均点に分散が生じ，過学習が発生してしまうような問題において，大量のパラメタや関数形そのものを手動調整するのは正気の沙汰ではない．Optunaに投げるという強硬手段もあるが，私のような計算機貧乏がそれをやったところでまともな結果にならない，というのをAHC003で私は強く学習していた．

やっぱり，評価関数は解釈可能なものであって欲しい．何らかの形で最終的にかかる所要時間を近似するものであって欲しい．

上述したとりあえず難しいタスクを押し付けて簡単なタスクは後回しにするチートができてしまうことを除けば，20日間真面目に考えて残りを無限人近似してごまかすという考え方自体は(計算ができるかどうかはともかく)有望そうに見える．このチートは，「何に取り組み，何を後回しにするか選ばないといけないのに，後回しにしたものの結果に責任をもたない」ということから生まれてしまう．

それなら，固定するのを20日間の方ではなく最適化するべきタスクの方にしたらうまくいくのでは?と思いついた．タスクを並べ替えるだけで無限人近似でごまかす部分との依存関係をいじらないなら，こういう病的な現象は起こらない．下手にタスクを後回しにしたら，そのツケは無限人近似をされている部分で依存タスクが律速になり，全体が遅くなるだけである．

これでチートの方は解決できた．しかし，所要時間を最適化するのは，律速ではない部分の最適化が全く行われない，という結果にならないだろうか?

律速ではない部分が最適化できないのは，max関数が小さい方の値を完全に無視することから生まれる現象である．ならば，maxではなく小さい方の値を無視しないような関数に変えれば良い．しかし，これを変更してしまうことで，$T$の計算が$O(N)$でできなくなっては困る．

ちょっと考えると，クリティカルパスと$T$を求める動的計画法は，実はmaxと足し算という半環の操作しか使っていないということに気づいた．「maxを近似でき，でも小さい方の値を完全には無視せず，足し算と合わせて半環の公理を満たすようなものはなーんだ」というなぞなぞは，おそらくちょっと昔の(ディープ以前の)機械学習とか音声認識みたいなのを知っている人には馴染み深いもので，その答えはlogsumexpだ．つまり，maxをlogsumexpに入れ替えれば，$T$を求める動的計画法は実は全く変更しなくていいのだ．

律速ではない部分の最適化もこれでできるようになった．残るは計算時間の問題である．評価関数の更新にO(N)かかるのはまだ遅い．

これも，半環の操作による$T$の定義をよく考えると解決できた．$B^i$の初期値が変わる時，$T$を高速に求めろという問題は，半環の操作がlogsumexpと+であるということを忘れて整数の足し算と掛け算だと思えば，(アルゴリズムの)競プロerとっては典型ofthe典型の「DAGが与えられ，スタートからゴールまでの経路の本数を数えよ．ただしスタートから各頂点までに直接生えている辺の本数は更新されることがある．」という問題に化ける．当然ゴールから各地点までの経路の本数を持っておいて，スタートからその地点までの辺の本数が変わったらゴールからその地点までの経路の本数と一回だけ掛け算をして更新すれば良い．これの足し算と掛け算をそのままlogsumexpと足し算に置き換えてしまえば，変更されたタスクの個数分のみの計算時間で評価関数が増えたかどうかが計算できる³．

これで，最適化をするための評価関数とその高速な更新(増えたかどうかの判定だけであるが)が出揃ったので，あとは適当な遷移を書いて，山登り法を回した．解($S$内の各タスクを誰がどういう順番で処理するか)の更新の実装は結構大変だったが，本質ではないのでその話は省略する⁴．

これをやった結果，最終的には貪欲法の103.6kから105.6kまで伸びた．めっちゃ嬉しかった．

終盤(Day 10)

残りの時間は，あと少しだけ点数を伸ばせないかいくつか試して，結局伸ばさなかった．

• 山登り法で全部の遷移について決定的に試してみるというのは，計算量の調整がしにくいので，確率的に遷移するようにしてみた．しかしより時間はかかって得点は減ってしまったので，戻した．
• 計算時間のベンチマークをしてみると，logsumexpの計算だけで時間をかなりとっていたので，上述のlogとってからexpをまたとるのを減らす工夫をしたらかなり速くなった．これをすると山登り法を1周ではなく2周回せるかと思い，手元で時間制限なしでやってみると平均2点くらい上がったが，投げてみるとTLEしてしまったので，計算時間を速くするだけで他は何も変えなかった⁵．手元で評価する時にも時間制限つけて評価したいが，並列処理でたくさん評価するとなぜか一つあたりの実行時間が10秒前後まで伸びてしまってわからなかったんですよ...(評価時の何かのバグなのかもしれないし，論理CPUの数と物理CPUの数を間違えていたのかもしれない．あるいは最近のSIMDの闇魔術をコンパイラが勝手に吐いて，それを実行している間にクロック周波数が下がって他のプロセスの実行時間に影響が出たのかもしれないし，はたまた，実はIOが律速なのかもしれない．原因は私にはわからなかった．)
• 上述のニュートン法で$t_i$を求めるやつを試してみた．長くなるので詳細は省くが，Mills ratioの近似を勉強して書いた．手元では実際に1点ちょっと上がったが，投げると点数が下がってしまった．計算時間がそこそこかかるのでそれで推定に割く時間が減って精度が落ちたのかもしれないし，単に問題セットの分散のせいなのかもしれない．しかし，計算時間が伸びてしまうのはシステスで3000ケースあると怖いので，やめた．

最終提出は105.6kのコードからlogsumexpを高速化したものを出した．なぜか105.5kまで点数が下がってしまったが，手元ではほとんど変わらなかったので，分散のせいだと信じた．

終わってから解説と他の人の解法を聞いて

面白いなと思ったのは，依存関係を全部無視して線形計画法にして解いた人がいたこと．私はコンテスト中はひたすらどうやって依存関係を効率よく捌けるかばっかり考えていて，実はR=1000程度では依存関係がほとんどないに等しいこと，そして依存関係がなければ線形計画法で 厳密解 緩和解が求まることに気付けなかった．(追記: 線形計画問題では「あるタスクをAさんが半分やってBさんが残り半分やるのが一番早い」というような解が出てくるかもしれないので，なんとかしてそれを処理しないといけない．それでも所要時間のそこそこ良い下界は得られる．)最小費用流でコストを推定タスク処理時間(+いろんな工夫)にして解いたという人も複数人見かけたが，多分それも本質的には「依存関係を無視する」という意味では似た考え方で，私の中には欠けていた視点だったなぁ，と思った．この問題，「無限人近似」と「無依存近似」の二つの近似ができて，私はもっぱら前者を考えていたが，chokudaiさんが解説で言っていたように場合によって使い分けたら実は106k以上いけるのかもしれない．

上位の人の中に「無能な人を捨てた」という人が多くてびっくりした．本当はそうでない方が最適であって欲しいなぁ...

推定は，山登り法や焼きなまし法を使った人が多いみたい．MCMCを使ったという人もちらほらいた．焼きなまし法で最尤推定するのとMCMC(の一種のメトロポリス・ヘイスティングス法)はかなり近い関係にあり，メトロポリス・ヘイスティングス法では温度を下げきらない代わりに，最終的な値だけでなく，途中の情報も使って分布全体を復元する，という程度の違いでしかない．
今回のように推定にかけられる時間が短い時，メトロポリス・ヘイスティングス法とギブスサンプリングでどのくらい性能に違いが出るのか，かなり気になる．

感想

途中熾烈な開発競争が辛かったが，いろいろな考察ができて，しかも最終的にはちゃんと本質的な改善が効いて楽しかった．

邪悪な目標は達成できたが，修論を頑張ります...

1. 後から考えてみれば，正しい推定値だったとしても挿入される±3の乱数の分を入れることを忘れていた．本来は第二項が$\gamma_1\sqrt{\mathbb V_n[t_{i,j}]+3^2/3}$となるべき． ↩

2. 界隈ではモデル予測制御とかreceding horizon controlと呼ばれている． ↩

3. 評価関数の値を$O(1)$で更新するのは半環の操作だけではできず，環の引き算が必要になる．logsumexpと+は，理論的には引き算もできるが，小さい数に非常に大きな数を足されたものから大きい数を引いて戻すみたいな操作が必要で，計算精度的に厳しいので，現実的にはmaxと+と同じように半環として扱うことが多い．どうしても更新された評価関数の値，あるいは評価関数の値の差分が知りたいなら，セグメント木などを使って$O(\log |S|)$で更新を行うのが速いだろう．しかし山登り法をするだけならこれはいらなかったので，実装しなかった． ↩

4. 同じ人間に振られたタスクを順番にDoubly linked listで繋ぎ，それをいじって更新した．更新した時にはまず影響を受ける全ての$S$内のタスクにDFSでマークをつける必要があり，次にマークされた全てのタスクからトポロジカルソートの要領でタスクが行われる時間$\tilde A^i, \tilde B^i$を計算する．そのついでに更新前と更新後の$\tilde B^i + \bar B_i$を計算して全てのマークされたiでlogexpsumを取り，更新後が更新前より減ってたら全体の評価関数も減っているはずなので変更を確定させ，そうでなければ変更を巻き戻す．私は実装力のない人間なので，もちろん何度もバグに悩まされた． ↩

5. 今考えてみると，各タスクの更新後の値をメモっておくことで，次の更新時に更新前の値を再計算する必要がなくなり，計算時間がさらに半分になるはずなので，いけたのかもしれない． ↩