以前、1次元シュレーディンガー方程式を有限要素法で解きました。
「1次元シュレーディンガー方程式を有限要素法で解いてみる in Julia」
https://qiita.com/cometscome_phys/items/fbeaa92fcb4b6d8c6240
今回は、2次元シュレーディンガー方程式を有限要素で解いてみましょう。
その際、せっかくの有限要素法ですから、好きなメッシュでやりたいので、gmshというソフトウェアを使ってメッシュを作り、それを読み込んでシュレーディンガー方程式を解いてみましょう。ちょうどgmshをJuliaから使うことのできるパッケージgmsh.jlがありますので、これでメッシュを作成することにします。
今回の記事は以下のような構成になっています。
構成
- 2次元シュレーディンガー方程式を有限要素法で解く：理論
- gmsh.jlによるメッシュ作成
- gmsh.jlで作ったメッシュ：MSHフォーマットのJuliaでの読み込み
- 2次元シュレーディンガー方程式を有限要素法で解く：コード
- 2次元シュレーディンガー方程式の解のプロット
- 未解決の部分：Makie.jlでのプロット
Juliaのバージョンは1.3を使っています。
2次元シュレーディンガー方程式を有限要素法で解く：理論
まず、解きたい方程式は2次元シュレーディンガー方程式：
- \left( \frac{\partial^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\right) \psi(x,y) + V(x,y) \psi(x,y) = E \psi(x,y)
です。これは固有値方程式ですので、固有値方程式を有限要素法で解くことになります。
基本的な流れは1次元の時と同じです。
つまり、方程式を部分積分して変形し、小さな領域で波動関数を一次関数で近似します。
部分積分
まず、左から$\psi(x,y)^{\ast}$をかけます。そして部分積分を使うと、
\int_{\Omega} dS \left( \frac{\partial}{\partial x}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial x} \psi(x,y)\right) \\
+ \int_{\Omega} dS \left( \frac{\partial}{\partial y}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial y} \psi(x,y)\right)
+ \int_{\Omega} dS \psi^{\ast}(x,y) V(x,y) \psi(x,y) \\
= E \int_{\Omega} dS \psi^{\ast}(x,y) \psi(x,y)
となります。ここで、積分$\int_{\Omega} dS$は今考えたい領域$\Omega$での積分で、境界では波動関数はゼロとします。
微小領域分割
次に、領域$\Omega$を細かく分割します。
ここでは、2次元ですので、領域が微小な3角形に分割されているとします。$i$番目の三角形の領域$\Omega
_i$とします。この時、積分は
\sum_i \int_{\Omega_i} dS \left( \frac{\partial}{\partial x}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial x} \psi(x,y)\right) \\
+ \sum_i \int_{\Omega_i} dS \left( \frac{\partial}{\partial y}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial y} \psi(x,y)\right)
+ \sum_i \int_{\Omega_i} dS \psi^{\ast}(x,y) V(x,y) \psi(x,y) \\
= E \sum_i \int_{\Omega_i} dS \psi^{\ast}(x,y) \psi(x,y)
となります。
解の仮定
上の方程式を満たすような解を探します。
$i$番目の領域内において、関数が一次関数でかけると近似してみましょう。つまり、
\psi_i(x,y) = \alpha_i + \beta_i x + \gamma_i y
とします。ここで、$\psi_i(x,y)$は$i$番目の領域内での波動関数で、領域の境界で連続になるように決めます。
今、三角形で領域を近似しているので、その時の3点を$x_1,y_1$,$x_2,y_2$,$x_3,y_3$とします。
そして、この三点での値をそれぞれ$\psi_i(x_1,y_1)$,$\psi_i(x_2,y_2)$,$\psi_i(x_3,y_3)$としましょう。この3点を通るように$\alpha_i,\beta_i,\gamma_i$を決めます。つまり、
\left(
\begin{matrix}
1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3
\end{matrix}
\right)
\left(
\begin{matrix}
\alpha_i \\
\beta_i \\
\gamma_i
\end{matrix}
\right)
=
\left(
\begin{matrix}
\psi_i(x_1,y_1) \\
\psi_i(x_2,y_2) \\
\psi_i(x_3,y_3)
\end{matrix}
\right)
を満たすような$\alpha_i,\beta_i,\gamma_i$を求めれば良いということになります。
つまり、
\left(
\begin{matrix}
\alpha_i \\
\beta_i \\
\gamma_i
\end{matrix}
\right) = M \left(
\begin{matrix}
\psi_i(x_1,y_1) \\
\psi_i(x_2,y_2) \\
\psi_i(x_3,y_3)
\end{matrix}
\right) \\
M = \Delta^{-1} \\
\Delta = \left(
\begin{matrix}
1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3
\end{matrix}
\right)
となります。よって、このMを計算しておけば領域内での関数形が決まります。
$\alpha_i,\beta_i,\gamma_i$は
\alpha_i = \sum_{j=1}^3 M_{1j}^{(i)} \psi_i(x_j,y_j) \\
\beta_i = \sum_{j=1}^3 M_{2j}^{(i)} \psi_i(x_j,y_j) \\
\gamma_i = \sum_{j=1}^3 M_{3j}^{(i)} \psi_i(x_j,y_j)
となりますので、領域$\Omega_i$での波動関数は
\psi_i(x,y) = \sum_j L_j^{(i)}(x,y) \psi_i(x_j,y_j) \\
L_j^{(i)}(x,y) = M_{1j}^{(i)} + M_{2j}^{(i)} x + M_{3j}^{(i)} y
と書く事ができます。この形は、有限要素法の文献などでよくみる形だと思います。
運動エネルギー項の変形
ここまでくれば、あとは上の関数を代入して方程式を変形するだけです。
運動エネルギー項は一階微分をするとx,y依存性がなくなるため、積分が簡単にできて、
\int_{\Omega_i} dS \left( \frac{\partial}{\partial x}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial x} \psi(x,y)\right) =
\int_{\Omega_i} dS \sum_{\alpha \beta}
\psi_i(x_\alpha,y_\alpha)^{\ast}
M_{2\alpha}^{(i)} M_{2\beta}^{(i)}\psi_i(x_\beta,y_\beta) \\
= \sum_{\alpha \beta}
\psi_i(x_\alpha,y_\alpha)^{\ast}
S_i M_{2\alpha}^{(i)} M_{2\beta}^{(i)}\psi_i(x_\beta,y_\beta)
となります。ここで$S_i$はこの三角形の面積で、行列$\Delta$を使うと、$S_i = \det(\Delta)/2$となります。
y方向も同様に、
\int_{\Omega_i} dS \left( \frac{\partial}{\partial y}\psi^{\ast}(x,y)\right) \left( \frac{\partial}{\partial y} \psi(x,y)\right)
= \sum_{\alpha \beta}
\psi_i(x_\alpha,y_\alpha)^{\ast}
S_i M_{3\alpha}^{(i)} M_{3\beta}^{(i)}\psi_i(x_\beta,y_\beta)
となります。
右辺の項の積分
次に、右辺の項の積分です。
右辺は
\int_{\Omega_i} dS \psi^{\ast}(x,y) \psi(x,y) =
\sum_{\alpha \beta} \psi_i(x_\alpha,y_\alpha)^{\ast} \psi_i(x_\beta,y_\beta) \int_{\Omega_i} dS L_\alpha^{(i)}(x,y) L_\beta^{(i)}(x,y)
となります。
ここに出てくる積分ですが、任意の三角形形状での一次関数の積の積分です。
これを真面目にやろうとすると、ちょっとしんどいですよね。
実は、この積分には公式があり、
\int_{\Omega_i} dS L_1^l L_2^m L_3^n = 2 S_i \frac{l! m! n!}{(l+m+n+2)!}
というものがあるそうです。
l,m,nはべき乗ですので、l=0,m=1,n=1とかにすると今回の積分ができることになります。
よって、
B_{\alpha \beta}^{(i)} \equiv \int_{\Omega_i} dS L_\alpha^{(i)}(x,y) L_\beta^{(i)}(x,y)
は解析的に計算が可能です。
証明についてはこちらが詳しいです。
ポテンシャル項
左辺のポテンシャルの項は、その微小領域での$V(x,y)$の値が一定だと近似すると右辺と同様に解析的に計算できます。
また、微小領域で一次関数で近似しても、積分の公式に乗せる事ができるので解析的に積分できます。
方程式の形
以上から、シュレーディンガー方程式は
\sum_{\alpha \beta}
\psi_i(x_\alpha,y_\alpha)^{\ast} A_{\alpha \beta}^{(i)} \psi_i(x_\beta,y_\beta)
= E \sum_{\alpha \beta} \psi_i(x_\alpha,y_\alpha)^{\ast} B_{\alpha \beta}^{(i)} \psi_i(x_\beta,y_\beta)
となります。ここで、
A_{\alpha \beta}^{(i)} =
S_i M_{2\alpha}^{(i)} M_{2\beta}^{(i)} +
S_i M_{3\alpha}^{(i)} M_{3\beta}^{(i)} + V_i B_{\alpha \beta}^{(i)}
です。簡単のためポテンシャル項を領域内で定数とおきました。
ここまでくれば、一次元の時と同様に一般化固有値問題になっていますね。
したがって、
A \psi = E B \psi
という方程式を数値的に解けば良いということになります。
境界条件
最後に、境界条件について述べます。
今考えている領域の端での波動関数をゼロとすると、無限大ポテンシャルの量子井戸問題になります。
端での点はゼロと決めたので、この点は行列から除く事が可能です。これも一次元の時と同じです。
まとめ
以上より、二次元シュレーディンガー方程式も一般化固有値問題に帰着されました。
通常の固有値問題ではなく一般化固有値問題になる理由は、波動関数を規格直交ではない関数で展開しているからです。もし通常のように規格直交した関数を基底として持ってくれば、右辺の行列Bは単位行列になります。
gmsh.jlによるメッシュ作成
2次元シュレーディンガー方程式は三角形の領域に分割すれば解ける事がわかりました。
そこで、そのメッシュを作ってみます。
このメッシュを一からプログラムを書いて作ることは可能だとは思いますが、面倒です。そこで、フリーのソフトウェアの力を借りましょう。
gmsh.jlを使います。
add Gmshでパッケージをインストールしておいてください。
そして、
import Gmsh: gmsh
gmsh.initialize()
gmsh.option.setNumber("General.Terminal", 1)
gmsh.model.add("t1")
lc = 2e-2
gmsh.model.geo.addPoint(0, 0, 0, lc, 1)
gmsh.model.geo.addPoint(1, 0, 0, lc, 2)
gmsh.model.geo.addPoint(1, 1, 0, lc, 3)
gmsh.model.geo.addPoint(0, 1, 0, lc, 4)
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(2, 3, 2)
gmsh.model.geo.addLine(3, 4, 3)
gmsh.model.geo.addLine(4, 1, 4)
gmsh.model.geo.addCurveLoop([4, 1, 2, 3], 1)
gmsh.model.geo.addPlaneSurface([1], 1)
gmsh.model.geo.synchronize()
gmsh.model.mesh.generate(2)
gmsh.write("t1.msh")
gmsh.finalize()
を実行してみましょう。MSHフォーマットというフォーマットでファイルが書き出されます。
これをGmshで開いてみましょう。Macであれば
brew install gmsh
でインストールすることができます。
その結果、
と可視化することができます。
上では、長さ1の正方形を作りました。gmshの使い方は公式などを参考にしてみてください。
似た形状であれば、addPointのところを
gmsh.model.geo.addPoint(0, 0, 0, lc, 1)
gmsh.model.geo.addPoint(1, 0, 0, lc, 2)
gmsh.model.geo.addPoint(0.3, 0.2, 0, lc, 3)
gmsh.model.geo.addPoint(0, 1, 0, lc, 4)
とに変えたりすると、
こんな形状も作ることができます。
gmsh.jlで作ったメッシュ：MSHフォーマットのJuliaでの読み込み
次に、作ったMSHフォーマットを自前のコードで読み込むことを考えます。
ここにあるフォーマットの仕様を眺めながら、コードを書きます。
試行錯誤しながら作ったコードは以下の通りです。
module MSH
export MSHdata,get_triangles,get_trianglepoints,get_lines
struct MSHdata
nodes::Array{Float64,2}
meshes::Dict{Int64,Dict{Int64,Array{Int64,1}}}
function MSHdata(filename)
println("---------------------------")
println("MSH data file is used")
nodes,meshes = load(filename)
println("Done.")
println("---------------------------")
return new(nodes,meshes)
end
end
#GMSH version 4
#http://gmsh.info//doc/texinfo/#File-formats
#=
In the format description above, elementType is e.g.:
1
2-node line.
2
3-node triangle.
3
4-node quadrangle.
4
4-node tetrahedron.
=#
function get_triangles(data::MSHdata)
return data.meshes[2]
end
function get_lines(data::MSHdata)
return data.meshes[1]
end
function get_trianglepoints(data::MSHdata)
triangles = data.meshes[2]
println("num. of triangles: ",length(triangles))
trianglepoints = Array{Array{Float64,1}}(undef,3,length(triangles))
triangleindices = Array{Int64}(undef,3,length(triangles))
count = 0
#println(triangles)
for (i,points) in triangles
count += 1
triangleindices[1,i] = points[1]
trianglepoints[1,i] = data.nodes[1:3,points[1]]
triangleindices[2,i] = points[2]
trianglepoints[2,i] = data.nodes[1:3,points[2]]
triangleindices[3,i] = points[3]
trianglepoints[3,i] = data.nodes[1:3,points[3]]
end
#println(trianglepoints)
return trianglepoints,triangleindices
end
function isstringfound(data,s)
for i=1:length(data)
u = split(data[i])
#println(u)
if u[1] == s
#println("found")
return i
# break
end
end
println("$s is not found!")
exit()
end
function load(filename)
data = readlines(filename)
imeshformat = isstringfound(data,"\$MeshFormat")
iendmeshformat = isstringfound(data,"\$EndMeshFormat")
#println("$imeshformat $iendmeshformat")
ver = split(data[imeshformat+1])[1]
println("The version is $ver")
inodes = isstringfound(data,"\$Nodes")
iendnodes = isstringfound(data,"\$EndNodes")
u = split(data[inodes+1])
numEntityBlocks = parse(Int64,u[1])
numNodes = parse(Int64,u[2])
minNodeTag = parse(Int64,u[3])
maxNodeTag = parse(Int64,u[4])
println("num of nodes: ", numNodes)
nodes = zeros(3,numNodes)
#exit()
position = inodes+1
nodecount = 0
for ie = 1:numEntityBlocks
position += 1
u = split(data[position])
entityDim = parse(Int64,u[1])
entityTag = parse(Int64,u[2])
parametric = parse(Int64,u[3])
numNodesInBlock = parse(Int64,u[4])
#println(u)
nodeTags = zeros(Int64,numNodesInBlock)
icount = 0
for inode = 1:numNodesInBlock
position += 1
icount +=1
u = split(data[position])
nodeTags[icount] = parse(Int64,u[1])
end
for inode = 1:numNodesInBlock
position += 1
nodecount += 1
u = split(data[position])
#println(nodeTags[inode])
nodes[1:3,nodeTags[inode]] = parse.(Float64,u[1:3])
end
end
if nodecount != numNodes
println("error! nodecount should be numNodes! nodecout = $nodecount numNodes = $numNodes")
exit()
end
#for i=1:numNodes
# println(nodes[:,i])
#end
ielements = isstringfound(data,"\$Elements")
iendelements = isstringfound(data,"\$EndElements")
position = ielements+1
u = split(data[position])
numEntityBlocks = parse(Int64,u[1])
numElements = parse(Int64,u[2])
minElementTag = parse(Int64,u[3])
maxElementTag = parse(Int64,u[4])
meshes = Dict{Int64,Dict{Int64,Array{Int64,1}}}()
numelements = Dict{Int64,Int64}()
for ie = 1:numEntityBlocks
position += 1
u = split(data[position])
entityDim = parse(Int64,u[1])
entityTag = parse(Int64,u[2])
elementType = parse(Int64,u[3])
numElementsInBlock = parse(Int64,u[4])
if haskey(meshes,elementType) == false
meshes[elementType] = Dict{Int64,Array{Int64,1}}()
numelements[elementType] = 0
end
#println(elementType)
for ielement = 1:numElementsInBlock
position += 1
numelements[elementType] += 1
u = split(data[position])
id = parse(Int64,u[1])
inodes = parse.(Int64,u[2:end])
meshes[elementType][numelements[elementType] ] = inodes[:]
end
end
#println(meshes)
return nodes,meshes
end
end
loadというfunctionがメインです。仕様にしたがってファイルを読んでいき、点の位置と要素の位置と形状をDict型に格納しています。
三角形の他には線分や三次元形状のものもありますが、それら全て読み込み、MSHdataというtypeに格納しました。ですので、3次元の計算をしたい場合もこのmodule MSHは使いまわすことが可能です。
2次元シュレーディンガー方程式を有限要素法で解く：コード
さて、上のコードを使えば、三角形領域を取り出すことができるようになりました。
いよいよ本体のコードです。nodeを結節点、elementを三角形の要素とします。
メッシュのロード
まず、二つのTypeを作ってみました。
struct Element
r::Array{Array{Float64,1}}
S::Float64
M::Array{Float64,2}
indices::Array{Int64,1}
function Element(r1,r2,r3,indices)
rs = Array{Array{Float64,1}}(undef,3)
rs[1] = r1
rs[2] = r2
rs[3] = r3
M,S = calc_M(rs)
return new(rs,S,M,indices)
end
end
function calc_M(rs::Array{Array{Float64,1}})
Δ = zeros(Float64,3,3)
Δ[:,1] .= 1
for i=1:3
Δ[i,2] =rs[i][1]
Δ[i,3] =rs[i][2]
end
M = inv(Δ)
S = det(Δ)/2 #Area
return M,S
end
struct Set_of_Elements
Nelements::Int64
Nnodes::Int64
elements::Array{Element,1}
nodes::Array{Float64,2}
lines::Dict{Int64,Array{Int64,1}}
insideindices::Array{Int64,1}
function Set_of_Elements(filename)
mshdata = MSHdata(filename)
triangles,triangleindices = get_trianglepoints(mshdata)
lines = get_lines(mshdata)
Nelements = size(triangles)[2]
nodes= mshdata.nodes[:,:]
Nnodes = size(nodes)[2]
elements = Array{Element,1}(undef,Nelements)
for i=1:Nelements
r1 = triangles[1,i]
r2 = triangles[2,i]
r3 = triangles[3,i]
indices = triangleindices[:,i]
element = Element(r1,r2,r3,indices)
elements[i] = element
end
insideindices = get_boundaries(lines,nodes)
return new(Nelements,Nnodes,elements,nodes,lines,insideindices)
end
end
function get_boundaries(lines,nodes)
Nlines = length(lines)
Nnodes = size(nodes)[2]
BCnodes = Set{Int64}()
count = 0
for (i,line) in lines
i1 = line[1]
i2 = line[2]
push!(BCnodes,i1)
push!(BCnodes,i2)
end
numBC = length(BCnodes)
Nfinitenodes =Nnodes - numBC
indices = Array{Int64,1}(undef,Nfinitenodes)
icount =0
for i=1:Nnodes
if issubset(i,BCnodes) == false
icount += 1
indices[icount] = i
end
end
println("Matrix dimension is ",Nfinitenodes)
return indices
end
Element typeはi番目の要素に関する情報を格納しています。行列Mや面積S、三点の座標などです。また、点としてどれを使っているかのindexをindicesに格納しています。
Set_of_Elements typeはメッシュ全体の情報を格納するtypeです。MSHdata(filename)で先ほど作ったmoduleからメッシュデータを読み込みます。また、波動関数をゼロにする境界については、MSHフォーマットではlineとして格納されていますので、そのlineに含まれるnodeの座標以外の座標をinsideindicesとして集めます。
fieldの取得
Set_of_Elements typeの中身を取り出すにはドット.をつければできますが、可読性が下がります。そこで、
function get_S(se::Set_of_Elements,i)
return se.elements[i].S
end
function get_M(se::Set_of_Elements,i)
return se.elements[i].M[:,:]
end
function get_points(se::Set_of_Elements,i)
r1 = se.elements[i].r[1][:]
r2 = se.elements[i].r[2][:]
r3 = se.elements[i].r[3][:]
return r1,r2,r3
end
function get_indices(se::Set_of_Elements,i)
return se.elements[i].indices[:]
end
と作っておきます。
A行列の作成
A行列を作成します。このコードでは簡単のためポテンシャルはゼロにしました。
function Ax_element(se::Set_of_Elements,ie)
Ax = zeros(Float64,3,3)
M = get_M(se,ie)
S = get_S(se,ie)
for j=1:3
for i=1:3
Ax[i,j] = M[2,i]*M[2,j]
end
end
return S*Ax
end
function Ay_element(se::Set_of_Elements,ie)
Ay = zeros(Float64,3,3)
M = get_M(se,ie)
S = get_S(se,ie)
for j=1:3
for i=1:3
Ay[i,j] = M[3,i]*M[3,j]
end
end
return S*Ay
end
function make_Amatrix(se::Set_of_Elements)
Nnodes = se.Nnodes
Nelements = se.Nelements
A = zeros(Float64,Nnodes,Nnodes)
for i=1:Nelements
Ax = Ax_element(se,i)
Ay = Ay_element(se,i)
r1,r2,r3 = get_points(se,i)
indices = get_indices(se,i)
for j=1:3
index_j = indices[j]
for i=1:3
index_i = indices[i]
A[index_i,index_j] += Ax[i,j] + Ay[i,j]
end
end
end
return A
end
これは定義通りですね。
結節点の数と同じサイズの行列Aを定義しています。
B行列の作成
次に、B行列です。
function make_Bmatrix(se::Set_of_Elements)
Nnodes = se.Nnodes
Nelements = se.Nelements
B = zeros(Float64,Nnodes,Nnodes)
for ie=1:Nelements
r1,r2,r3 = get_points(se,ie)
indices = get_indices(se,ie)
for j=1:3
index_j = indices[j]
for i=1:3
index_i = indices[i]
l = 0
m = 0
n = 0
l += ifelse(j==1,1,0)
l += ifelse(i==1,1,0)
m += ifelse(j==2,1,0)
m += ifelse(i==2,1,0)
n += ifelse(j==3,1,0)
n += ifelse(i==3,1,0)
L123 = calc_L123(se.elements[ie],l,m,n)
B[index_i,index_j] += L123
end
end
end
return B
end
function calc_L123(ele::Element,l,m,n)
return 2*ele.S*(factorial(l)*factorial(m)*factorial(n))/factorial(l+m+n+2)
end
これは積分公式を使いました。定義通りですね。
行列の作成と境界条件の適用
次に、作った行列A,Bに境界条件を適用します。今回は端の点をゼロとしています。
function make_matrixAB(se::Set_of_Elements)
A = make_Amatrix(se)
B = make_Bmatrix(se)
A,B,indices = apply_BC(se,A,B)
return A,B
end
function apply_BC(se::Set_of_Elements,A,B)
indices = se.insideindices[:]
#println(indices)
Atmp = A[indices,indices]
Btmp = B[indices,indices]
return Atmp,Btmp,indices
end
apply_BCでは行列サイズを小さくしています。Juliaの面白い機能として、必要なindex
だけをArrayで集めておくと、A[indices,indices]みたいにすると小さな行列を作ることができます。
全体のコード
以上で全部です。書き出しなどもつけた全体のコードは
include("msh.jl")
module FE
using LinearAlgebra
using ..MSH
export Set_of_Elements,get_indices
struct Element
r::Array{Array{Float64,1}}
S::Float64
M::Array{Float64,2}
indices::Array{Int64,1}
function Element(r1,r2,r3,indices)
rs = Array{Array{Float64,1}}(undef,3)
rs[1] = r1
rs[2] = r2
rs[3] = r3
M,S = calc_M(rs)
return new(rs,S,M,indices)
end
end
struct Set_of_Elements
Nelements::Int64
Nnodes::Int64
elements::Array{Element,1}
nodes::Array{Float64,2}
lines::Dict{Int64,Array{Int64,1}}
insideindices::Array{Int64,1}
function Set_of_Elements(filename)
mshdata = MSHdata(filename)
triangles,triangleindices = get_trianglepoints(mshdata)
lines = get_lines(mshdata)
Nelements = size(triangles)[2]
nodes= mshdata.nodes[:,:]
Nnodes = size(nodes)[2]
elements = Array{Element,1}(undef,Nelements)
for i=1:Nelements
r1 = triangles[1,i]
r2 = triangles[2,i]
r3 = triangles[3,i]
indices = triangleindices[:,i]
element = Element(r1,r2,r3,indices)
elements[i] = element
end
insideindices = get_boundaries(lines,nodes)
return new(Nelements,Nnodes,elements,nodes,lines,insideindices)
end
end
function get_S(se::Set_of_Elements,i)
return se.elements[i].S
end
function get_M(se::Set_of_Elements,i)
return se.elements[i].M[:,:]
end
function get_points(se::Set_of_Elements,i)
r1 = se.elements[i].r[1][:]
r2 = se.elements[i].r[2][:]
r3 = se.elements[i].r[3][:]
return r1,r2,r3
end
function get_indices(se::Set_of_Elements,i)
return se.elements[i].indices[:]
end
function Ax_element(se::Set_of_Elements,ie)
Ax = zeros(Float64,3,3)
M = get_M(se,ie)
S = get_S(se,ie)
for j=1:3
for i=1:3
Ax[i,j] = M[2,i]*M[2,j]
end
end
return S*Ax
end
function Ay_element(se::Set_of_Elements,ie)
Ay = zeros(Float64,3,3)
M = get_M(se,ie)
S = get_S(se,ie)
for j=1:3
for i=1:3
Ay[i,j] = M[3,i]*M[3,j]
end
end
return S*Ay
end
function make_Amatrix(se::Set_of_Elements)
Nnodes = se.Nnodes
Nelements = se.Nelements
A = zeros(Float64,Nnodes,Nnodes)
for i=1:Nelements
Ax = Ax_element(se,i)
Ay = Ay_element(se,i)
r1,r2,r3 = get_points(se,i)
indices = get_indices(se,i)
for j=1:3
index_j = indices[j]
for i=1:3
index_i = indices[i]
A[index_i,index_j] += Ax[i,j] + Ay[i,j]
end
end
end
return A
end
function make_Bmatrix(se::Set_of_Elements)
Nnodes = se.Nnodes
Nelements = se.Nelements
B = zeros(Float64,Nnodes,Nnodes)
for ie=1:Nelements
r1,r2,r3 = get_points(se,ie)
indices = get_indices(se,ie)
for j=1:3
index_j = indices[j]
for i=1:3
index_i = indices[i]
l = 0
m = 0
n = 0
l += ifelse(j==1,1,0)
l += ifelse(i==1,1,0)
m += ifelse(j==2,1,0)
m += ifelse(i==2,1,0)
n += ifelse(j==3,1,0)
n += ifelse(i==3,1,0)
L123 = calc_L123(se.elements[ie],l,m,n)
B[index_i,index_j] += L123
end
end
end
return B
end
function get_boundaries(lines,nodes)
Nlines = length(lines)
Nnodes = size(nodes)[2]
BCnodes = Set{Int64}()
count = 0
for (i,line) in lines
i1 = line[1]
i2 = line[2]
push!(BCnodes,i1)
push!(BCnodes,i2)
#println("$i1 $i2")
end
numBC = length(BCnodes)
#println(BCnodes)
Nfinitenodes =Nnodes - numBC
indices = Array{Int64,1}(undef,Nfinitenodes)
icount =0
for i=1:Nnodes
if issubset(i,BCnodes) == false
icount += 1
indices[icount] = i
end
end
println("Matrix dimension is ",Nfinitenodes)
return indices
end
function apply_BC(se::Set_of_Elements,A,B)
indices = se.insideindices[:]
#println(indices)
Atmp = A[indices,indices]
Btmp = B[indices,indices]
return Atmp,Btmp,indices
end
function make_matrixAB(se::Set_of_Elements)
A = make_Amatrix(se)
B = make_Bmatrix(se)
A,B,indices = apply_BC(se,A,B)
return A,B
end
function calc_L123(ele::Element,l,m,n)
return 2*ele.S*(factorial(l)*factorial(m)*factorial(n))/factorial(l+m+n+2)
end
function calc_M(rs::Array{Array{Float64,1}})
Δ = zeros(Float64,3,3)
Δ[:,1] .= 1
for i=1:3
Δ[i,2] =rs[i][1]
Δ[i,3] =rs[i][2]
end
M = inv(Δ)
S = det(Δ)/2 #Area
return M,S
end
end
using .FE
using LinearAlgebra
function test()
L = 1
elements = Set_of_Elements(ARGS[1]*".msh")
A,B = FE.make_matrixAB(elements)
F = eigen(A, B)
#println(F.values)
fp = open(ARGS[1]*"_"*"eigvalues.dat","w")
for i=1:length(F.values)
println(fp,i,"\t",F.values[i],"\t")
end
close(fp)
fp = open(ARGS[1]*"_"*"eigvalues_exact.dat","w")
i = 0
nxmax = 1000
nymax = 1000
enes = zeros(Float64,nxmax*nymax)
for nx=1:nxmax
for ny=1:nxmax
i += 1
ene = π^2*(nx^2+ny^2)
enes[i] = ene
end
end
sort!(enes)
for i=1:nxmax*nymax
println(fp,i,"\t",enes[i],"\t")
end
close(fp)
Nnodes = elements.Nnodes
bindices = elements.insideindices[:]
data = zeros(Float64,Nnodes)
count = 0
for index in bindices
count += 1
data[index] =F.vectors[count,1]
end
fp = open(ARGS[1]*"_"*"groundstate.dat","w")
for i=1:Nnodes
node = elements.nodes[:,i]
println(fp,node[1],"\t",node[2],"\t",data[i])
end
close(fp)
return elements,F
end
elements,F = test()
となります。MSHフォーマットを呼び出すコードはmsh.jlとして保存しています。
一般化固有値問題は、Juliaでは
eigen(A, B)
だけで解くことができて便利です。
実行は
julia 2d.jl t1
という感じで行います。ここで、t1というのはt1.mshというファイルから読み出すという意味になります。
2次元シュレーディンガー方程式の解のプロット
それでは、解いてみましょう。
まずは、一つ目の正方形を解きます。すると、
---------------------------
MSH data file is used
The version is 4.1
num of nodes: 3435
Done.
---------------------------
num. of triangles: 6668
Matrix dimension is 3235
と出力されます。結節点の数が3435、三角形の数が6668、行列の次元が3235です。ここで、200ほど少ないのは、境界での波動関数をゼロとしたためです。
正方形
長さ1の正方形でポテンシャルがない場合、最初に書いた微分方程式の固有値は（1/2mなどは無視していることに注意あるいはm=0.5としているとみなしても良いです。）
E(n_x,n_y) = \pi^2 (n_x^2+n_y^2)
となります。
比較してみると、
となります。100番目くらいまでは大体合ってますね。
あとはメッシュを細かくすればもっと合っていきます。
最低エネルギーの波動関数は
となります。よくみる形ですね。
追記
メッシュを規則正しくした場合はどうなるでしょうか？
import Gmsh: gmsh
gmsh.initialize()
gmsh.option.setNumber("General.Terminal", 1)
gmsh.model.add("t1")
lc = 1.8e-2
gmsh.model.geo.addPoint(0, 0, 0, lc, 1)
gmsh.model.geo.addPoint(1, 0, 0, lc, 2)
gmsh.model.geo.addPoint(1, 1, 0, lc, 3)
gmsh.model.geo.addPoint(0, 1, 0, lc, 4)
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(2, 3, 2)
gmsh.model.geo.addLine(3, 4, 3)
gmsh.model.geo.addLine(4, 1, 4)
gmsh.model.geo.addCurveLoop([4, 1, 2, 3], 1)
gmsh.model.geo.addPlaneSurface([1], 1)
gmsh.model.setPhysicalName(2, 1, "My surface")
gmsh.model.geo.synchronize()
gmsh.model.mesh.setTransfiniteSurface(1,"AlternateLeft")
gmsh.model.mesh.generate(2)
gmsh.write("t1_test.msh")
gmsh.finalize()
としてみました。gmsh.model.setPhysicalName(2, 1, "My surface")とgmsh.model.mesh.setTransfiniteSurface(1,"AlternateLeft")が変更点です。
結果は
Info : Meshing 1D...
Info : Meshing curve 1 (Line)
Info : Meshing curve 2 (Line)
Info : Meshing curve 3 (Line)
Info : Meshing curve 4 (Line)
Info : Done meshing 1D (0.000479 s)
Info : Meshing 2D...
Info : Meshing surface 1 (transfinite)
Info : Done meshing 2D (0.000801 s)
Info : 3249 vertices 6500 elements
Info : Writing 't1_test.msh'...
Info : Done writing 't1_test.msh'
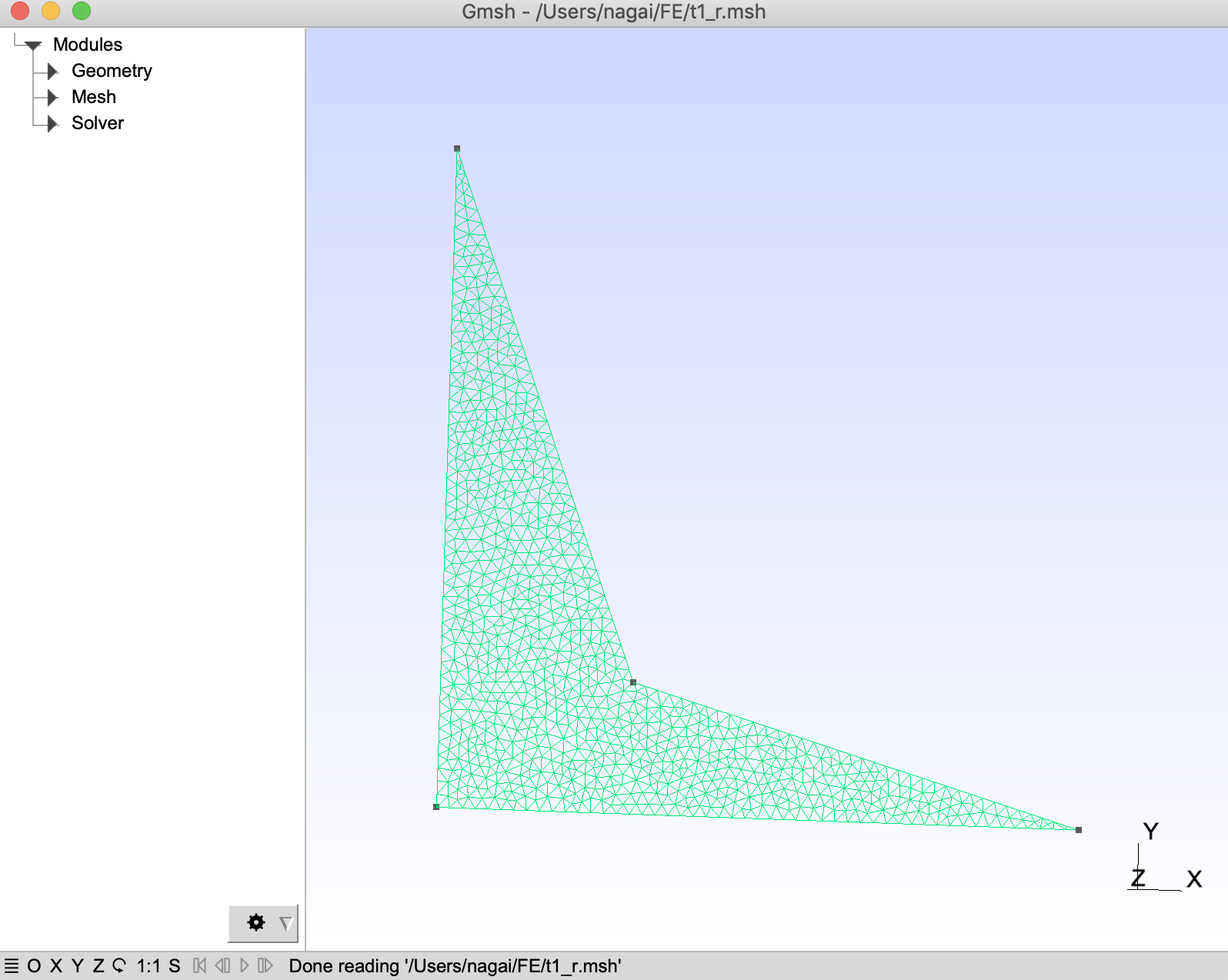
となり、メッシュの数は同じくらいにしました。
その時のグリットは
となります。これで固有値を計算してみると、
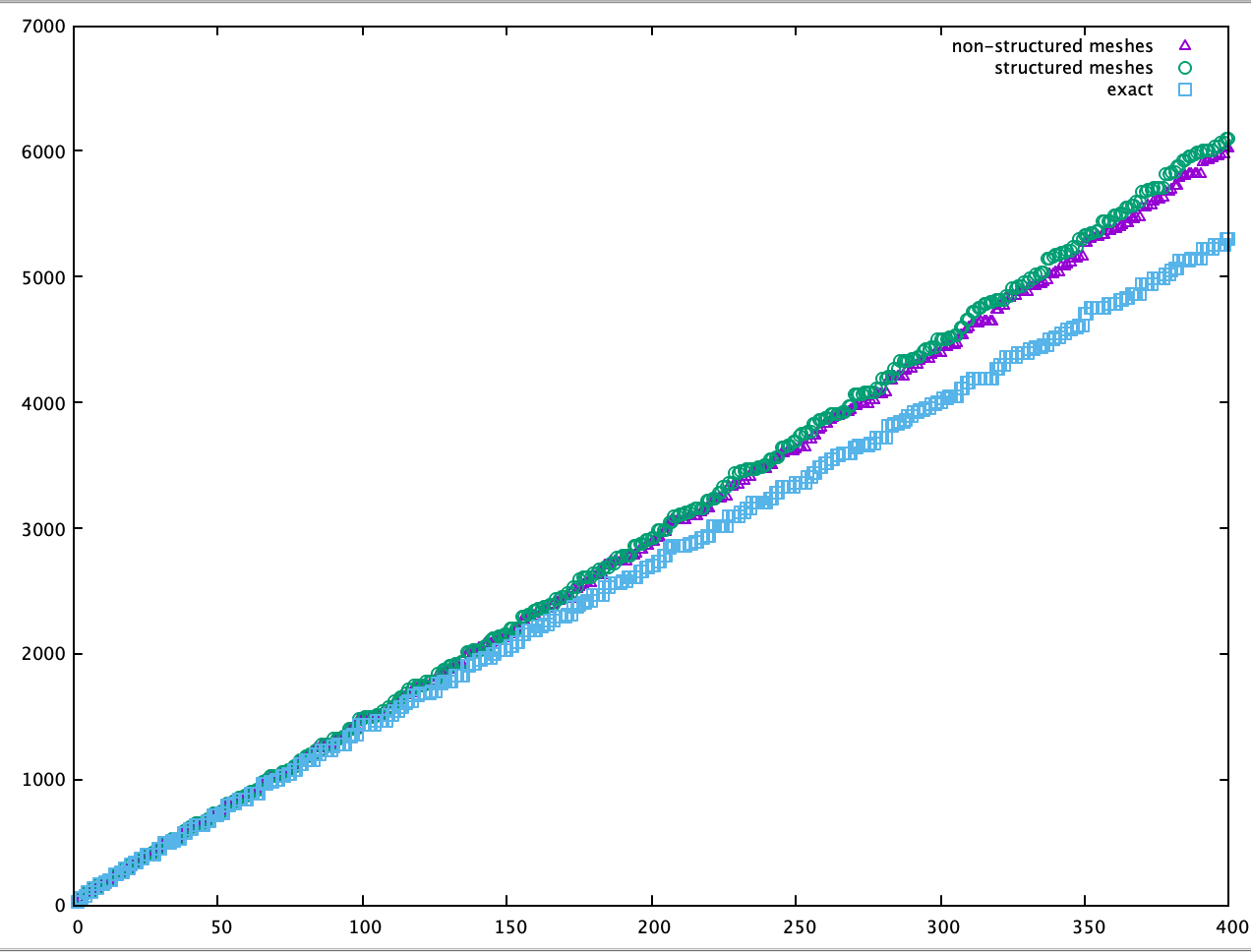となりました。規則正しい方が若干ズレが大きいように見えます。不思議ですね。
変な形
次に、二番目の形状の計算をしてみましょう。
その最低エネルギーの波動関数の絶対値の二乗は
となります。それっぽい感じですね。
Makie.jlでのプロット
Makieでのプロットの方法がわかりましたので、追記します。こちらを参考にしました。
プロット用のコードは
using Makie
using GLMakie
using AbstractPlotting
using FileIO
function plot_groundwavefunction(se::Set_of_Elements,F)
Nnodes = se.Nnodes
Nelements = se.Nelements
bindices = se.insideindices[:]
coordinates = zeros(Float64,Nnodes,2) #座標点の情報を格納
data = zeros(Float64,Nnodes)
count = 0
for i=1:Nnodes
coordinates[i,:] = se.nodes[1:2,i]
end
for index in bindices
count += 1
data[index] =abs(F.vectors[count,1])^2 #境界以外の部分だけ格納されているので、そこを取り出す。
end
connectivity = zeros(Int64,Nelements,3) #三角形のindexの情報を格納
for i=1:Nelements
indices = get_indices(se,i)
connectivity[i,:] = indices[:]
end
scene = mesh(coordinates, connectivity, color = data, shading = false,scale_plot =false)
wireframe!(scene[end][1], color = (:black, 0.6), linewidth = 0.1)
Makie.save("groundstate.png", scene)
end
plot_groundwavefunction(elements,F)
となります。coordinatesに結節点の座標、connectivityに有限要素の三角形のindex、colorに値を入れればOKです。meshで色を塗って、wireframe!で有限要素メッシュの線を描画しています。
結果は、
こんな感じになります。ちゃんとメッシュが描かれていますね。