1次元シュレーディンガー方程式を有限要素法で解いてみる in Julia

量子力学で現れる1次元シュレーディンガー方程式を差分化して解くことはこれまでやってきましたので、今回は有限要素法で解いてみましょう。
有限要素法を用いると、固有値問題は一般化固有値問題へと変わります。
言語はJuliaを用います。Juliaでは一般化固有値問題$Ax =EBx$もeigen(A, B)とすれば簡単に解けますので、便利です。

参考文献：
「水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる（C++のソースコード付き）」
https://qiita.com/dc1394/items/c0d3d02fa738b040128c
「数値計算で学ぶ量子力学: プログラミング言語Juliaによる数値計算入門」
http://park.itc.u-tokyo.ac.jp/kato-yusuke-lab/nagai/JuliaQM.pdf

バージョン

Julia 1.3

シュレーディンガー方程式

1次元シュレーディンガー方程式は

- \frac{d^2}{dx^2} \psi(x) + V(x) \psi(x) = E \psi(x)

です。ここで、無次元化を行っています。また、系は$0 \le x \le L$を考え、その外側は無限大ポテンシャルがあるとします（量子井戸）。
つまり、$\psi(0) = \psi(L) = 0$という境界条件を考えます。

厳密解

この方程式はV=0なら手で解くことができて、エネルギー固有値は

E = n^2 \frac{\pi^2}{L^2}

となります。

シュレーディンガー方程式の変形

この方程式に左から$\psi^{\ast}(x)$をかけて、積分すると、

- \int_0^L dx \psi^{\ast}(x) \frac{d^2}{dx^2} \psi(x) + \int_0^L dx \psi^{\ast}(x)  V(x) \psi(x) = E \int_0^L dx \psi^{\ast}(x) \psi(x)

となり、部分積分を実行すると、

\int_0^L dx \left( \frac{d}{dx}\psi^{\ast}(x)\right) \left( \frac{d}{dx} \psi(x)\right) + \int_0^L dx \psi^{\ast}(x)  V(x) \psi(x) = E \int_0^L dx \psi^{\ast}(x) \psi(x)

となります。ここで、部分積分を実行する際に境界条件$\psi(0) = \psi(L) = 0$を用いました。
次に、積分をN分割します。

\sum_{e=0}^{N-1} \left[  \int_{x_0^e}^{x_1^e} dx  \left( \frac{d}{dx}\psi^{\ast}(x)\right) \left( \frac{d}{dx} \psi(x)\right) + \int_{x_0^e}^{x_1^e} dx\psi^{\ast}(x)  V(x) \psi(x) \right] = E\sum_{e=0}^{N-1} \int_{x_0^e}^{x_1^e} dx \psi^{\ast}(x) \psi(x)

ここで、$x_0^e,x_1^e$はe番目の結節点の座標です。例えば、$x_1^0 = x_0^1$となっています。
結節点の数は全部でN+1個になっています。

関数の展開

上記の方程式を満たす解としてどのようなものが良いでしょうか？
まず、分割した積分のうちe番目の区間$x_0^e \le x \le x_1^e$を考えます。ここで、

x = x_0^e +y l^e \\
l^e = x_1^e-x_0^e

という変数yを導入し変数変換すると、

\sum_{e=0}^{N-1} \left[  \int_{0}^{1}dy \frac{1}{l^e}  \left(\frac{d}{dy}\psi^{\ast}(y)\right) \left( \frac{d}{dy} \psi(y)\right) + \int_{0}^{1} dy l^e \psi^{\ast}(y)  V(y) \psi(y) \right] = E\sum_{e=0}^{N-1} \int_{0}^{1} dy l^e \psi^{\ast}(y) \psi(y)

となります。
ここで、この区間での波動関数を

\psi(y) = \sum_{i=0}^{1} \psi_i^e \phi_i(y), \: (x_0^e \le x \le x_1^e) \\
\phi_0(y) = 1-y \\
\phi_1(y) = y

という形に仮定します。これは、

\psi(y) = (1-y) \psi_0^e + y \psi_1^e

という形ですので、区間の両端を$\psi(x_0^e) =\psi_0^e$および$\psi(x_1^e) =\psi_1^e$として、その間を直線で近似していることに対応しています。
ここで、波動関数は連続関数であるべきことから、$\psi_1^{e} = \psi_0^{e+1}$という関係があります。

さて、関数形を仮定しましたので、積分を手で実行できるようになりました。
微分を含む項は、

\frac{d}{dy}\psi(y) = - \psi_0^e +  \psi_1^e

より、

\int_{0}^{1}dy \left(\frac{d}{dy}\psi^{\ast}(y)\right) \left( \frac{d}{dy} \psi(y)\right) =\int_{0}^{1}dy (- \psi_0^{e\ast} +  \psi_1^{e\ast})(- \psi_0^e +  \psi_1^e) \\
= \left( \begin{matrix}
\psi_0^{e \ast} & \psi_1^{e \ast}
\end{matrix}
\right)
\left( \begin{matrix}
1 & -1 \\
-1 & 1
\end{matrix}
\right)
\left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)

となります。右辺は、

\int_0^{1}dy ((1-y) \psi_0^{e\ast} + y \psi_1^{e\ast})((1-y) \psi_0^e + y \psi_1^e) = 
\int_0^{1}dy
\left( \begin{matrix}
\psi_0^{e \ast} & \psi_1^{e \ast}
\end{matrix}
\right)
\left( \begin{matrix}
(1-y)(1-y) & (1-y)y \\
y(1-y) & y^2
\end{matrix}
\right)
\left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right) \\
= \frac{1}{6}
\left( \begin{matrix}
\psi_0^{e \ast} & \psi_1^{e \ast}
\end{matrix}
\right)
\left( \begin{matrix}
2 & 1 \\
1 & 2
\end{matrix}
\right)
\left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)

となりますので、全体は、

\sum_{e=0}^{N-1} 
\left( \begin{matrix}
\psi_0^{e \ast} & \psi_1^{e \ast}
\end{matrix}
\right)
\hat{A}
\left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)
= E \sum_{e=0}^{N-1}  \left( \begin{matrix}
\psi_0^{e \ast} & \psi_1^{e \ast}
\end{matrix}
\right) \hat{B} \left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)

\hat{A} \equiv \frac{1}{l^e} \left( \begin{matrix}
1+V_{00} & -1+V_{01} \\
-1 + V_{10} & 1 + V_{11}
\end{matrix}
\right) \\
\hat{B} \equiv \frac{l^e}{6}
\left( \begin{matrix}
2 & 1 \\
1 & 2
\end{matrix}
\right) \\
\hat{V} = \left( \begin{matrix}
V_{00}  &V_{01}  \\
V_{10}  & V_{11} 
\end{matrix}
\right) \\
= l^e \left( \begin{matrix}
(1-y)(1-y)V(y) & (1-y)yV(y) \\
y(1-y)V(y) & y^2V(y)
\end{matrix}
\right)

となります。
この方程式を満たすような解を求めたい場合、変分原理を用いればよくて、
ここから、一般化固有値問題：

\sum_{e=0}^{N-1}
\hat{A}
\left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)
= E \sum_{e=0}^{N-1} \hat{B} \left( \begin{matrix}
\psi_0^{e} \\ \psi_1^{e}
\end{matrix}
\right)

が出てきます。
$\psi_1^{e} = \psi_0^{e+1}$という関係がありますので、それぞれのeに関する方程式は独立ではなく、現れる行列のサイズはN+1となります。

境界条件

上記の一般化固有値問題において、境界条件$\psi(0) = \psi(L) = 0$を考慮します。これは、左端の結節点と右端の結節点での波動関数の値がゼロであることを意味しているので、
AおよびBの最初の1行と1列、およびN+1行とN+1行の値を削ります。

コード

typeの定義

まず、typeを定義しておきましょう。module FEを作り、内部に以下のように定義します。

    mutable struct Felements
        N::Int64
        seg::Array{Array{Float64,1},1}
        le::Array{Float64,1}
        A::Array{Float64,2}
        B::Array{Float64,2}
    end

    function get_l(felements::Felements,e)
        return felements.le[e+1]
    end

このFelements typeに対して色々定義します。

コンストラクタ

コンストラクタは

    function Felements(x)
        N = length(x)
        seg = make_segments(x)
        le = calc_length(seg)
        A = zeros(Float64,N-2,N-2)
        B = zeros(Float64,N-2,N-2)
        felements = Felements(N,seg,le,A,B)
        A,B = make_matrix_AB(felements)
        return Felements(N,seg,le,A,B)
    end

とします。xは座標が入ります。ここに出てきているfunctionはそれぞれ

    function make_segments(vec_x)
        N = length(vec_x)
        vec_segments = Array{Array{Float64,1},1}(undef,N-1)
        for i=1:N-1
            vec_segments[i] = [vec_x[i],vec_x[i+1]]
        end
        return vec_segments
    end

    function calc_length(vec_segments)
        N = length(vec_segments)+1
        le = zeros(Float64,N-1)
        for i=1:N-1
            le[i] = vec_segments[i][2]-vec_segments[i][1]
        end
        return le
    end

    function A_element(felements::Felements,e,i,j)
        if i==0 && j==0
            v = 1
        elseif i==0 && j==1
            v = -1 
        elseif i==1 && j==0
            v = -1
        else
            v = 1
        end
        return v/get_l(felements,e)
    end

    function B_element(felements::Felements,e,i,j)
        if i==0 && j==0
            v = 2
        elseif i==0 && j==1
            v = 1 
        elseif i==1 && j==0
            v = 1
        else
            v = 2
        end
        return get_l(felements,e)*v/6
    end   

    function make_elementmatrices(felements::Felements,e)
        Ae = zeros(Float64,2,2)
        Be = zeros(Float64,2,2)

        for i=0:1
            for j=0:1
                Ae[i+1,j+1] = A_element(felements,e,i,j)
                Be[i+1,j+1] = B_element(felements,e,i,j)
            end
        end

        return Ae,Be
    end

    function make_matrix_AB(felements::Felements)
        N = felements.N
        Atmp = zeros(Float64,N,N)
        Btmp = zeros(Float64,N,N)
        A = zeros(Float64,N-2,N-2)
        B = zeros(Float64,N-2,N-2)
        for e=0:N-2
            Ae,Be= make_elementmatrices(felements,e)
            Atmp[e+1:e+2,e+1:e+2] += Ae[1:2,1:2]
            Btmp[e+1:e+2,e+1:e+2] += Be[1:2,1:2]
        end
        A[1:N-2,1:N-2] = Atmp[2:N-1,2:N-1]
        B[1:N-2,1:N-2] = Btmp[2:N-1,2:N-1]

        return A,B
    end

としました。最後のfunction make_matrix_ABでは、境界条件を満たすために行列のサイズを削っています。

対角化

これで一般化固有値問題の行列が作成できましたので、あとは解くだけです。

using .FE
using LinearAlgebra
function test()
    M = 100
    L = 10.0
    x = collect(range(0,L,length=M))
    felements = Felements(x)
    #println(inv(felements.B)*felements.A)
    F = eigen(felements.A, felements.B)
    println(F.values)
    fp = open("eigvalues.dat","w")
    for i=1:length(F.values)
        println(fp,i,"\t",F.values[i],"\t",π^2*i^2/(L)^2)
    end
    close(fp)
    fp = open("vector.dat","w")
    for i=2:length(x)-1
        println(fp,x[i],"\t",F.vectors[i-1,1])
    end
    close(fp)

end

test()

ここでは、長さLを10、結節点の数を100としました。

全体のコード

全体のコードは

module FE
    export Felements 

    mutable struct Felements
        N::Int64
        seg::Array{Array{Float64,1},1}
        le::Array{Float64,1}
        A::Array{Float64,2}
        B::Array{Float64,2}
    end

    function Felements(x)
        N = length(x)
        seg = make_segments(x)
        le = calc_length(seg)
        A = zeros(Float64,N-2,N-2)
        B = zeros(Float64,N-2,N-2)
        felements = Felements(N,seg,le,A,B)
        A,B = make_matrix_AB(felements)
        return Felements(N,seg,le,A,B)
    end

    function get_l(felements::Felements,e)
        return felements.le[e+1]
    end

    function make_segments(vec_x)
        N = length(vec_x)
        vec_segments = Array{Array{Float64,1},1}(undef,N-1)
        for i=1:N-1
            vec_segments[i] = [vec_x[i],vec_x[i+1]]
        end
        return vec_segments
    end

    function calc_length(vec_segments)
        N = length(vec_segments)+1
        le = zeros(Float64,N-1)
        for i=1:N-1
            le[i] = vec_segments[i][2]-vec_segments[i][1]
        end
        return le
    end

    function A_element(felements::Felements,e,i,j)
        if i==0 && j==0
            v = 1
        elseif i==0 && j==1
            v = -1 
        elseif i==1 && j==0
            v = -1
        else
            v = 1
        end
        return v/get_l(felements,e)
    end

    function B_element(felements::Felements,e,i,j)
        if i==0 && j==0
            v = 2
        elseif i==0 && j==1
            v = 1 
        elseif i==1 && j==0
            v = 1
        else
            v = 2
        end
        return get_l(felements,e)*v/6
    end    

    function make_elementmatrices(felements::Felements,e)
        Ae = zeros(Float64,2,2)
        Be = zeros(Float64,2,2)

        for i=0:1
            for j=0:1
                Ae[i+1,j+1] = A_element(felements,e,i,j)
                Be[i+1,j+1] = B_element(felements,e,i,j)
            end
        end

        return Ae,Be
    end

    function make_matrix_AB(felements::Felements)
        N = felements.N
        Atmp = zeros(Float64,N,N)
        Btmp = zeros(Float64,N,N)
        A = zeros(Float64,N-2,N-2)
        B = zeros(Float64,N-2,N-2)
        for e=0:N-2
            Ae,Be= make_elementmatrices(felements,e)
            Atmp[e+1:e+2,e+1:e+2] += Ae[1:2,1:2]
            Btmp[e+1:e+2,e+1:e+2] += Be[1:2,1:2]
        end
        A[1:N-2,1:N-2] = Atmp[2:N-1,2:N-1]
        B[1:N-2,1:N-2] = Btmp[2:N-1,2:N-1]

        return A,B
    end



end

using .FE
using LinearAlgebra
function test()
    M = 100
    L = 10.0
    x = collect(range(0,L,length=M))
    felements = Felements(x)
    #println(inv(felements.B)*felements.A)
    F = eigen(felements.A, felements.B)
    println(F.values)
    fp = open("eigvalues.dat","w")
    for i=1:length(F.values)
        println(fp,i,"\t",F.values[i],"\t",π^2*i^2/(L)^2)
    end
    close(fp)
    fp = open("vector.dat","w")
    for i=2:length(x)-1
        println(fp,x[i],"\t",F.vectors[i-1,1])
    end
    close(fp)

end

test()

となります。

厳密解との比較

手で解いて得られたエネルギー固有値を比較してみましょう。

全体の固有値は

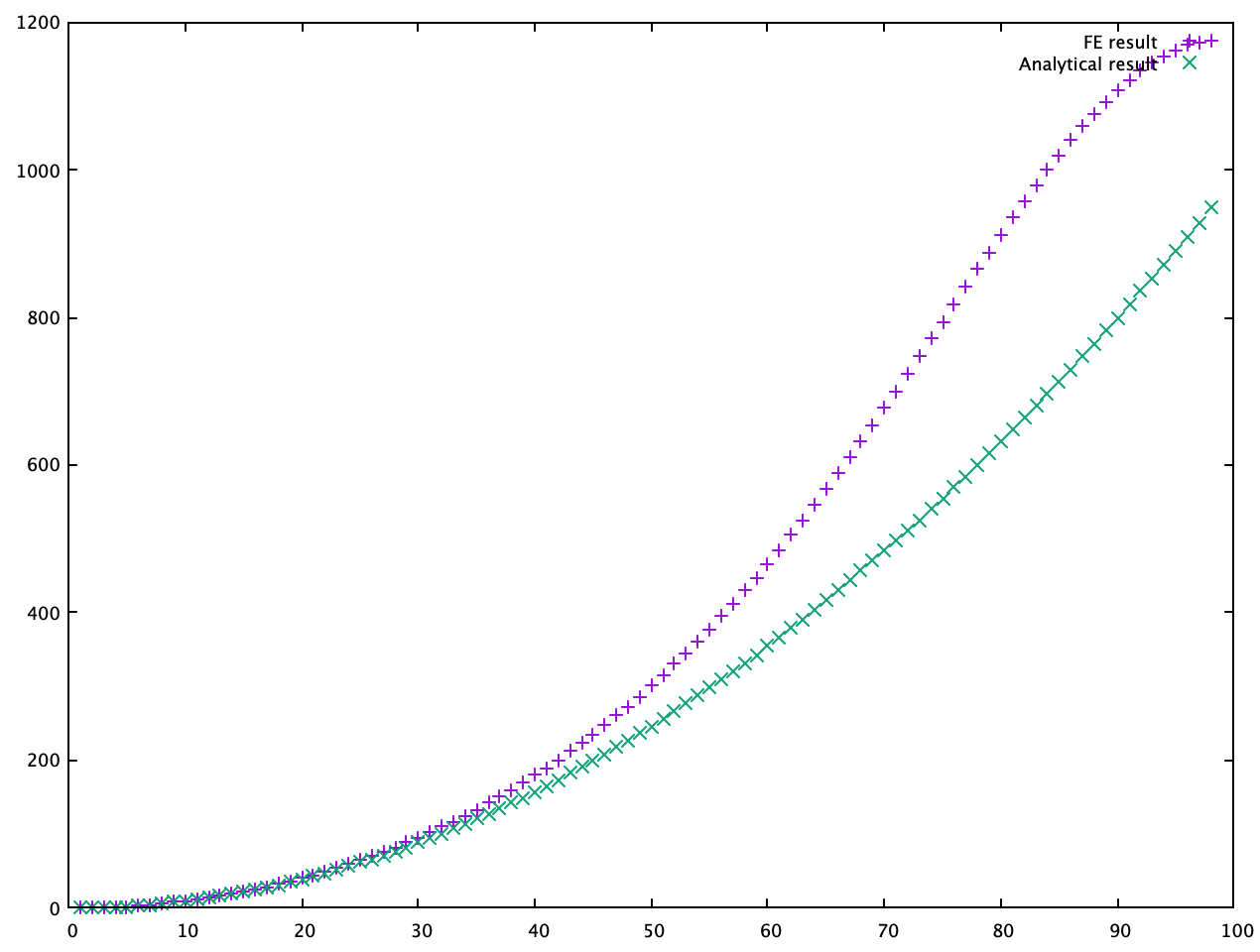となりました。有限要素法は線を有限個の数で分割していますので、その分割の線分の長さよりも短いスケールで振動する波動関数は記述できません。そのため、高エネルギーの解はちゃんと再現できませんので、高エネルギーではずれます。どのくらいのエネルギーからずれるかは、分割の数によって変わります。

一方、低エネルギーの固有値は

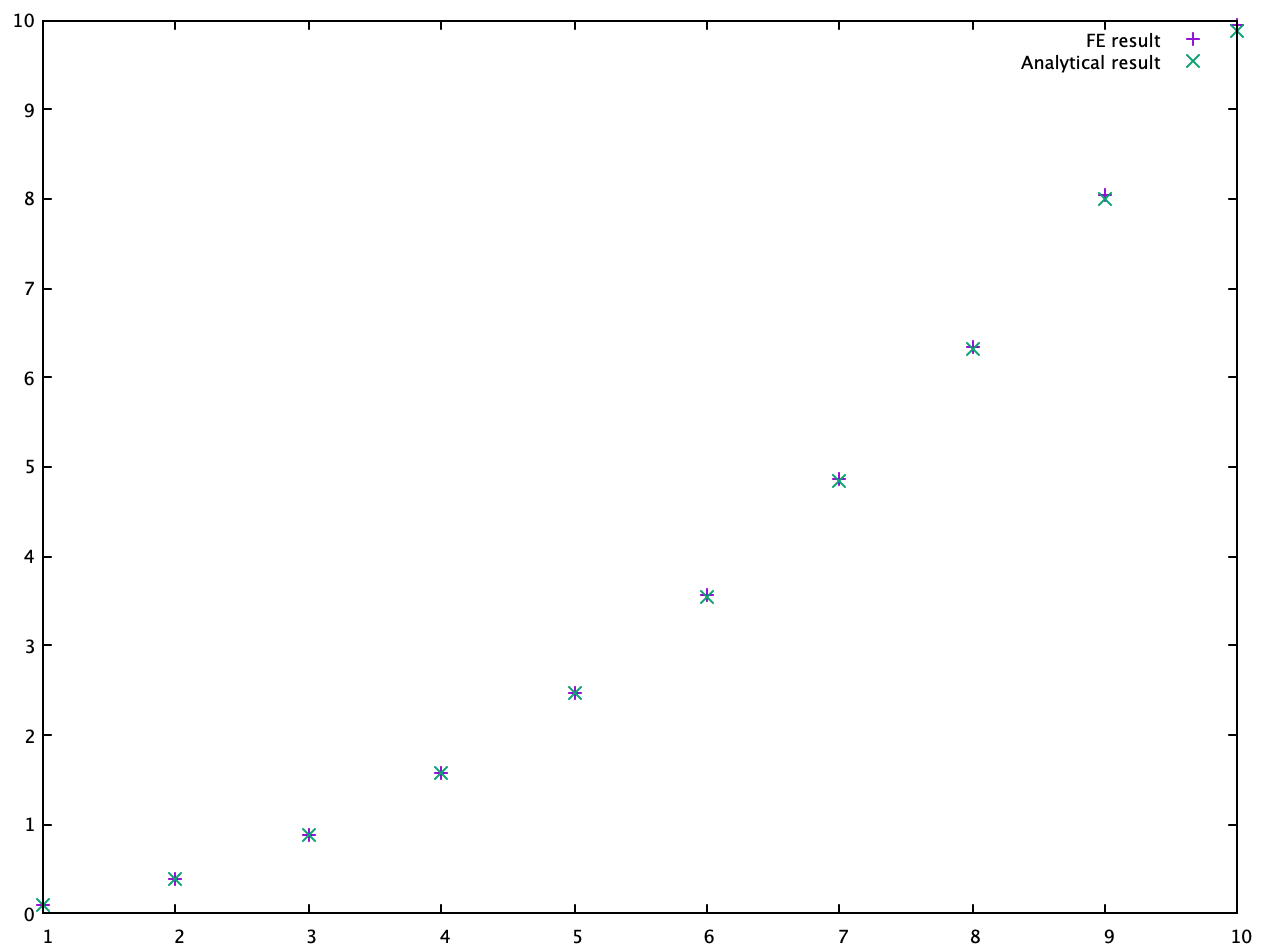となり、よく一致していることがわかります。