PyTorchで関数フィッティング

PyTorchが1.0になったらしいので、TensorFlowとJulia言語機械学習フレームワーク(Knet.jlとFlux.jl)しか触ったことがないけれども、見よう見まねでコードを書いてみる。

目的は、
「JuliaでTensorFlow その5: ニューラルネットワークの導入と深層学習」
https://qiita.com/cometscome_phys/items/45017aa9741c5fdc7eb9
「TensorFlowの高レベルAPIの使用方法：tf.layersの使い方と重みなどの取り出し方」
https://qiita.com/cometscome_phys/items/95ed1b89acc7829950dd

などで使っていた関数をPyTorchでも再現することである。

バージョン

PyTorch: 1.0.0
Python: 3.6.4

再現すべき関数

test.py

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

n = 10
x0 = np.linspace(-2.0, 2.0, n)
a0 = 3.0
a1 = 2.0
b0 = 1.0
y0 = np.zeros((n,1),dtype = 'Float32')
y0[:,0] = a0*x0+a1*x0**2 + b0 + 3*np.cos(20*x0)

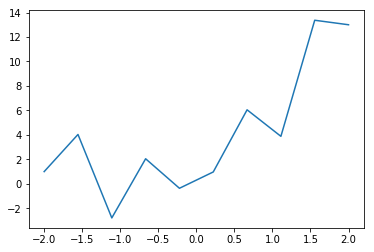
plt.plot(x0,y0 )
plt.show()
plt.savefig("graph.png")

このグラフをフィッティングするにあたって、
インプットは多項式でとする（これまでの記事を参照）。
隠れ層が何もなければ多項式による線形回帰となる。インプットは

test.py

def make_phi(x0,n,k):    
    phi = np.array([x0**j for j in range(k)])
    return phi.T

k = 4
phi = make_phi(x0,n,k)
print(phi[0,:])
d_input = k
d_middle = 10

で定義しておく。

モデルの定義

PyTorchでは以下のようにモデルを定義する。

import torch 
import torch.nn as nn 
import torch.nn.functional as F
from torch.autograd import Variable
import torch.optim as optim

class Net(nn.Module):
    def __init__(self,d_inp,d_middle,d_out):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(d_inp,d_middle)
        self.fc2 = nn.Linear(d_middle, d_out)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)        
        return x

ここで、モデルのニューラルネットワークのサイズを作成時に決められるようにしておいた。
これで、隠れ層一層のニューラルネットワークとなっている。
モデルは、

d_out = 1
net = Net(d_input,d_middle,d_out)

で作られる。

loss関数と最適化

次に、loss関数とその最適化を決める。
TensorFlowでは先にグラフを作っていたが、PyTorchでは先にグラフを作らない。

learning_rate = 0.001

print(net)
params = list(net.parameters())
print(params)

これで、ネットワークがどのようになっているか、と、最適化すべきパラメータに何があるかがわかる。
インプットと正解データをテンソルとして用意するには、

input = torch.from_numpy(phi[:,:])
target = torch.from_numpy(y0)

とすればよい。
そして、loss関数は平均二乗誤差：

criterion = nn.MSELoss()

を選び、最適化にはADAM:

optimizer = optim.Adam(net.parameters(), lr=learning_rate)

を使用することとする。

#学習

学習は、

nt = 20000
for i in range(nt):
    optimizer.zero_grad() #勾配の初期化？　必要らしい
    output = net(input) #アウトプットの生成
    loss = criterion(output, target) #loss関数
    loss.backward() 
    optimizer.step()
    if i %1000 is 0:
        print(i,loss.item())

print(params[:])      
print('Finished Training')
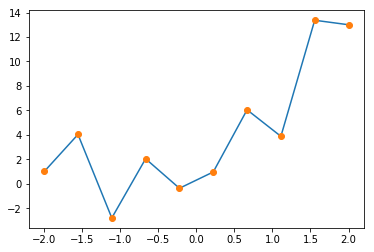
ye = net(input).detach().numpy()
plt.plot(x0,y0 )
plt.plot(x0,ye,'o')
plt.show()
plt.savefig("graph_2.png")

となる。

得られた図は

である。

#全体のコード

全体のコードは

import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline   # Jupyter用

n = 10
x0 = np.linspace(-2.0, 2.0, n)
a0 = 3.0
a1 = 2.0
b0 = 1.0
y0 = np.zeros((n,1),dtype = 'Float32')
y0[:,0] = a0*x0+a1*x0**2 + b0 + 3*np.cos(20*x0)

plt.plot(x0,y0 )
#plt.show()
plt.savefig("graph.png")

def make_phi(x0,n,k):    
    phi = np.array([x0**j for j in range(k)],dtype = 'Float32')
    return phi.T

k = 4
phi = make_phi(x0,n,k)
print(phi[0,:])
d_input = k
d_middle = 10

import torch 
import torch.nn as nn 
import torch.nn.functional as F
from torch.autograd import Variable
import torch.optim as optim


learning_rate = 0.001


class Net(nn.Module):
    def __init__(self,d_inp,d_middle,d_out):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(d_inp,d_middle)
        self.fc2 = nn.Linear(d_middle, d_out)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)        
        return x

d_out = 1
net = Net(d_input,d_middle,d_out)
print(net)
params = list(net.parameters())
print(params)

input = torch.from_numpy(phi[:,:])
target = torch.from_numpy(y0)

criterion = nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr=learning_rate)

nt = 20000

for i in range(nt):
    optimizer.zero_grad()
    output = net(input)
    loss = criterion(output, target)
    loss.backward()
    optimizer.step()
    if i %1000 is 0:
        print(i,loss.item())

print(params[:])      
print('Finished Training')
ye = net(input).detach().numpy()
plt.plot(x0,y0 )
plt.plot(x0,ye,'o')
#plt.show()
plt.savefig("graph_2.png")

となる。