物理から作るスイカゲーム

0.はじめに

Siv3D Advent Calendar 2023の13日目。初めての参加です。Siv3D標準搭載の物理演算は用いず、簡単な物理から作ってみようという内容です。記事を書くのは初めてなので分かりにくくても多めにみてください><

1.簡単な物理処理を書こう

スイカゲームは円と壁しかないので、今回はそれしか実装しません。まず始めに用いる物理公式はこちら。
$t$：時間,　$x$：重心位置,　$θ$：回転角度,　$v$：速度,　$ω$：角速度, 　$M$：質量, 　$I$：慣性モーメント, 　$P$：力積　$r$：重心からの位置ベクトル

• $Δx=vΔt$
• $Δθ=ωΔt$
• $ Δv=\frac{P}{M} $
• $Δω=\frac{r×P}{I}$ (外積)

もちろんこれらの式は、例えば$Δx=vΔt$なんかは$v$が時間に対して一定でないと成り立ちませんが、今回は気にしません。

物理あんまわかんない人向けにざっくりと説明します。上二つは時間経過による位置の変化、下二つは力積による動きの変化を表します。力積$P$は力$f$を$Δt$秒加えたとき$P=fΔt$で表される量です。質量$M$は力積が加えられたときの速度変化のしにくさを表しています。同様に、慣性モーメント$I$は力積が加えられたときの角速度変化のしにくさを表しています。角速度変化の場合は、同じ力積でも重心から遠い方が強く働き、回転方向成分のみが利くので、その分が$r×P$で表されています。

円盤の慣性モーメントは$I=\frac{1}{2}Mr^2$で表されます。
さっそくこれらを用いて実装します。

struct PhysicsCircle {
	Vec2 pos;//重心位置
	Vec2 v;//速度
	double theta;//回転角度
	double omega;//角速度
	double M;//質量
	double I;//慣性モーメント
	double r;//半径

	PhysicsCircle() = default;
	PhysicsCircle(const Vec2& center, double radius) {
		pos = center;
		r = radius;
		v = {};
		theta = 0;
		omega = 0;
		M = 1;
		I = 0.5 * M * r * r;
	}
	Circle circle() const {
		return Circle{ pos,r };
	}
	//重心を基準とした相対座標から力積を加える。
	void addImpulseLocal(const Vec2& impulse, const Vec2& addLocalPos) {
		v += impulse / M;
		omega += addLocalPos.cross(impulse) / I;
	}
	//絶対座標から力積を加える。
	void addImpulse(const Vec2& impulse, const Vec2& addPos) {
		addImpulseLocal(impulse, addPos - pos);
	}
	void update(double delta) {
		pos += v * delta;
		theta += omega * delta;
	}
	void draw(const ColorF& color = Palette::White) {
		circle().draw();
		Line{ pos,Arg::direction = Circular(r,theta).toVec2() }.draw(Palette::Black);
	}
};

式のまま実装したのがわかると思います。これだけですでに物理演算の根幹は完成しました。以下を実装してドラッグしてみると、それっぽい動きをします。

void Main()
{
	PhysicsCircle c{ Scene::CenterF(),100 };
	Vec2 downPos{};
	while (System::Update())
	{
		if (MouseL.down())downPos = Cursor::PosF();
		if (MouseL.up())c.addImpulse(Cursor::PosF() - downPos, downPos);
		c.update(Scene::DeltaTime());
		c.draw();
	}
}

重力の実装

毎フレーム速度に加算することで重力を表現します。

void Main()
{
	Array<PhysicsCircle> circles;

	while (System::Update())
	{
		double delta = Scene::DeltaTime();

		if (MouseL.down()) {
			circles.emplace_back(Cursor::PosF(), Random(10, 100));
		}

		for (auto& o : circles) {
			o.update(delta);
			o.v.y += 9.8 * 60 * delta;//重力
		}
		//描画
		for (auto& o : circles) {
			o.draw();
		}
	}
}

クリックでランダムな円が召喚できるような実装です。（重力をなんとなく9.8としていますが、あまり意味はありません。なんでもいいです。）
訂正：重力の加算にdeltaをかけるのを忘れておりました。

2.線との衝突

衝突処理においてやらなければいけないことは、①物同士が重なっていたらその分座標をずらして解消し、②衝突によって生じた力積を加えて運動を変化させることです。

2.1重なり解消

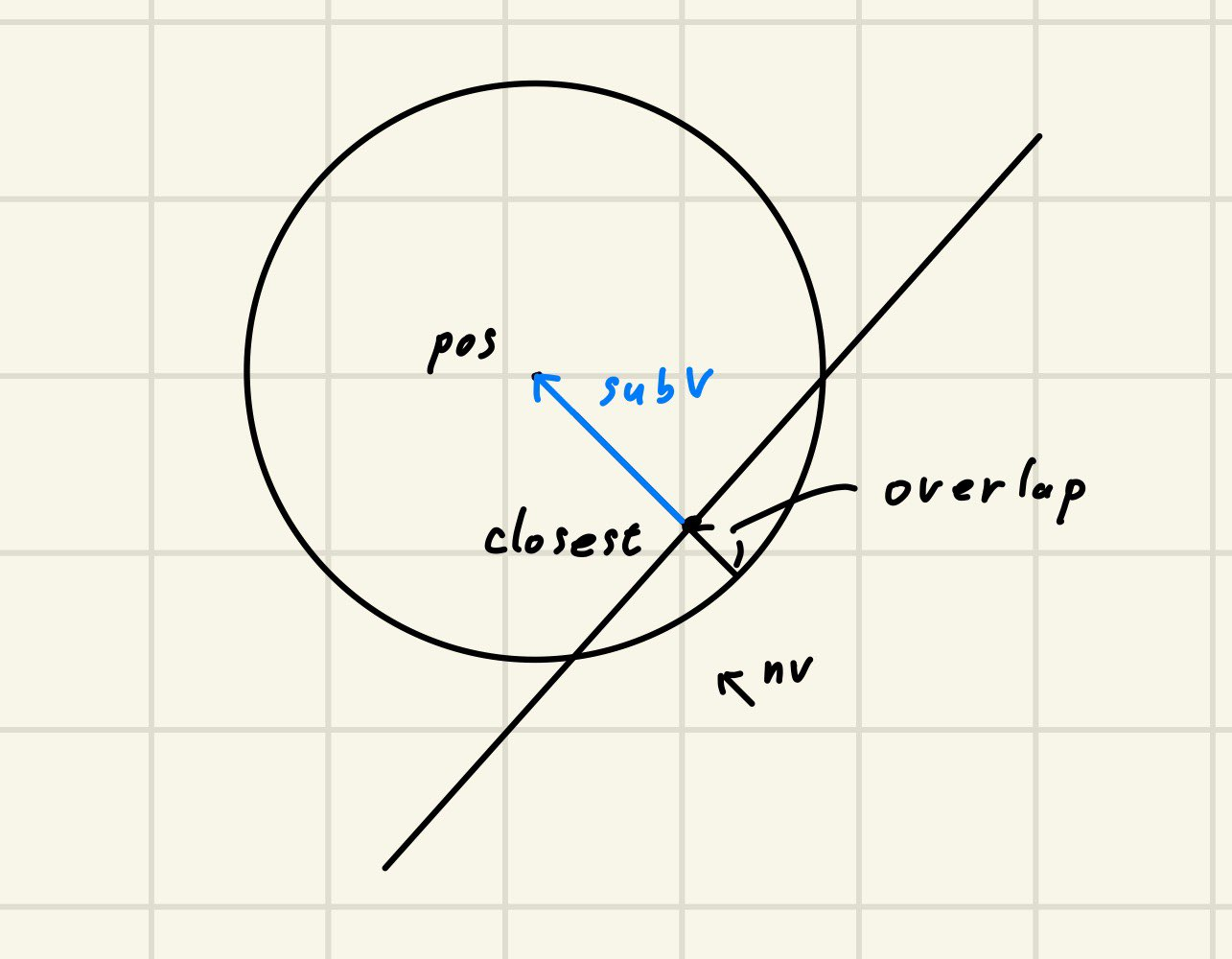
Siv3DにはありがたいことにLine::closet(Vec2 p)というLine上のpに一番近い点を求める関数がありますので、それを使っちゃいます。図におけるnvは衝突面の法線ベクトルです。半径-subVの長さでoverlapが計算でき、overlap*nvだけ円をずらしてあげればよいことがわかると思ます。

2.2垂直抗力

今回は簡単のため、衝突による跳ね返りをゼロとしましょう。つまり、衝突方向の速度が完全に打ち消されるような垂直抗力による力積が働きます。速度とnvとの内積によって衝突方向の速度成分を計算できます。力積は運動量変化に等しいので、この速度成分に質量をかけたものが、垂直抗力による力積です。

• $P=MΔv$

単純に打ち消すように速度を足してあげるだけでも良いですが、今回はより物理っぽく、そのような力積が加えられたというていで実装します。（後に実装する摩擦と統一的に実装できるメリットもある。）

※垂直抗力がかかる場所は、重心から見て-nv*rで計算できます。

void Main()
{
	Array<PhysicsCircle> circles;
	Array<Line> walls;

	walls.emplace_back(100, 300, 700, 600);
	walls.emplace_back(100, 700, 600, 500);
	circles.emplace_back( Scene::Center(),100 );

	while (System::Update())
	{
		double delta = Scene::DeltaTime();

		for (auto& o : circles) {
			o.update(delta);
			o.v.y += 9.8 * 60 * delta;//重力
		}
		//Circle と wall の衝突
		for (auto& pCircle : circles) {
			for (auto& wall : walls) {
				Vec2 subV = pCircle.pos - wall.closest(pCircle.pos);
				if (subV.isZero()) {
					continue;
				}
				double overlap = (pCircle.r - subV.length());
				if (overlap < 0) {//overlapが正なら衝突
					continue;
				}
				Vec2 nv = subV.normalized();
				pCircle.pos += nv * overlap;//重なり解消
				double dotV = -pCircle.v.dot(nv);//速度の衝突方向成分(衝突に向かう向きを正とする)
				if (dotV < 0) {//衝突方向に向かていないなら無視
					continue;
				}
				pCircle.addImpulseLocal(nv * dotV * pCircle.M, -nv * pCircle.r);//垂直効力
			}
		}

		//描画
		for (auto& o : circles) {
			o.draw();
		}
		for (auto& o : walls) {
			o.draw(ColorF(1, 0.5));
		}
	}
}

for文で円と壁をまわして、それぞれで重なり解消、垂直抗力の力積付与を行っています。

2.3摩擦力

今回は動摩擦力のみを計算します。
・$F=μN$
$F$：摩擦力　$μ$：動摩擦係数　$N$：垂直抗力
これが摩擦力の有名な式です。力積で考えると、摩擦による力積は、垂直抗力による力積に動摩擦係数をかけたもの。と捉えることが出来ます。垂直抗力の力積はdotV * pCircle.Mを用いればよいですね。動摩擦係数は適当に0.5としましょう。あとは摩擦がどの方向にかかるかを調べればよいです。

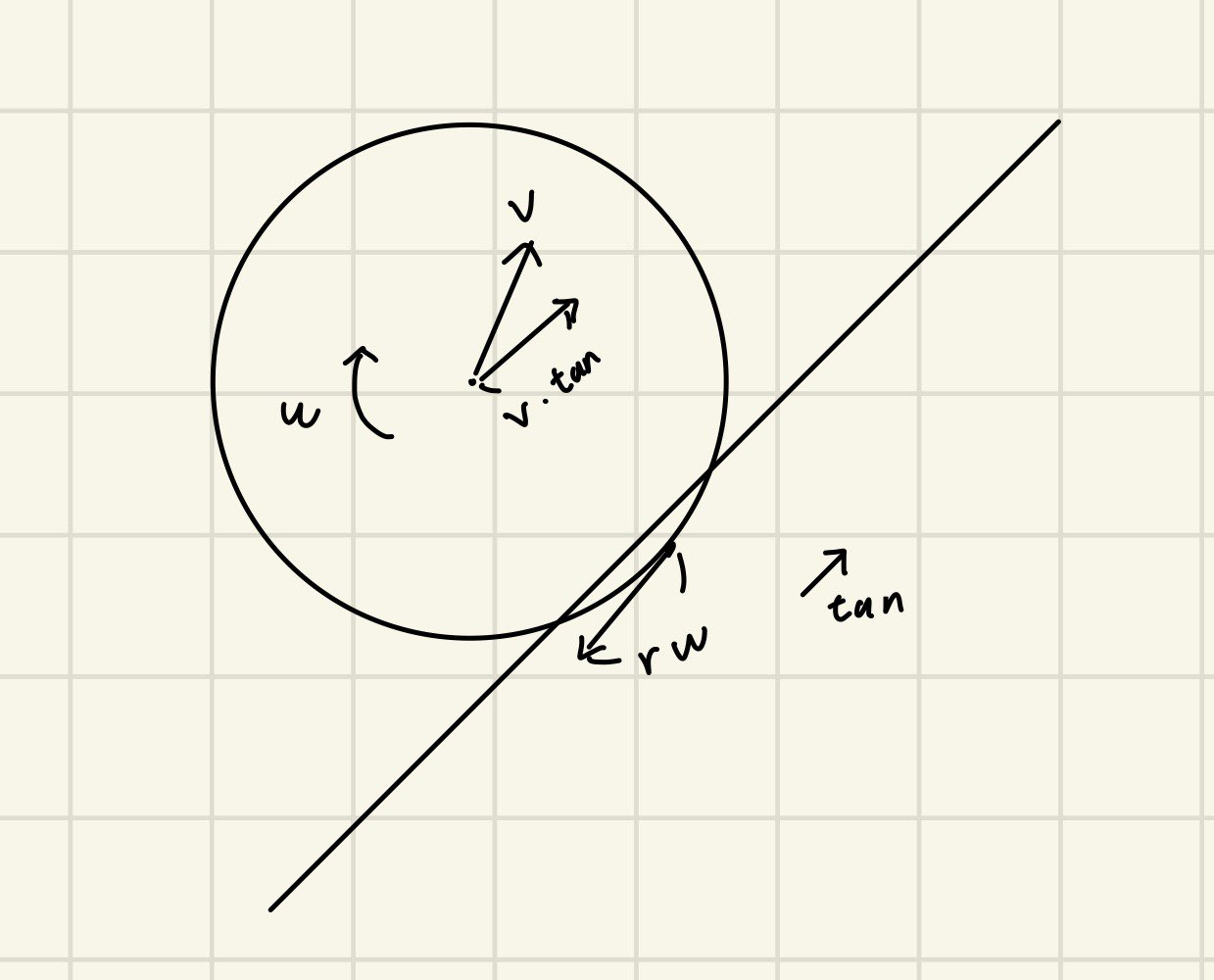
衝突面に平行な単位ベクトルをtanとすると、接点における速度は速度成分$v・tan$と回転成分$-rω$の和で表せます。（回転成分はtanにとって負の方向に寄与します）摩擦は、この速度を打ち消すような方向に働きます。

void Main()
{
	Array<PhysicsCircle> circles;
	Array<Line> walls;

	walls.emplace_back(100, 300, 700, 600);
	walls.emplace_back(100, 700, 600, 500);

	while (System::Update())
	{
		double delta = Scene::DeltaTime();

		if (MouseL.down()) {
			circles.emplace_back(Cursor::PosF(), Random(10, 100));
		}

		for (auto& o : circles) {
			o.update(delta);
			o.v.y += 9.8 * 60 * delta;//重力
		}
		//Circle と wall の衝突
		for (auto& pCircle : circles) {
			for (auto& wall : walls) {
				Vec2 subV = pCircle.pos - wall.closest(pCircle.pos);
				if (subV.isZero()) {
					continue;
				}
				double overlap = (pCircle.r - subV.length());
				if (overlap < 0) {//overlapが正なら衝突
					continue;
				}
				Vec2 nv = subV.normalized();
				pCircle.pos += nv * overlap;//重なり解消
				double dotV = -pCircle.v.dot(nv);//速度の衝突方向成分(衝突に向かう向きを正とする)
				if (dotV < 0) {//衝突方向に向かていないなら無視
					continue;
				}
+				Vec2 tan = nv.rotated90();
+				Vec2 fDir = -Sign(pCircle.v.dot(tan) - pCircle.r * pCircle.omega) * tan;//摩擦の方向ベクトル
+				pCircle.addImpulseLocal((nv + fDir * 0.5) * Min(dotV, 50.0) * pCircle.M, -nv * pCircle.r);//摩擦+垂直効力
-				pCircle.addImpulseLocal(nv * dotV * pCircle.M, -nv * pCircle.r);//垂直効力
			}
		}

		//描画
		for (auto& o : circles) {
			o.draw();
		}
		for (auto& o : walls) {
			o.draw(ColorF(1, 0.5));
		}
	}
}

dotVがMin(dotV,50.0)になっています。落下直後に強い摩擦がかかって好ましくないのを避けるために、50を上限としました。垂直抗力の成分が結合法則でまとまっていることに注意してください。

以上で線との衝突処理は終わりです。

３.円と円の衝突

3.1重なり解消

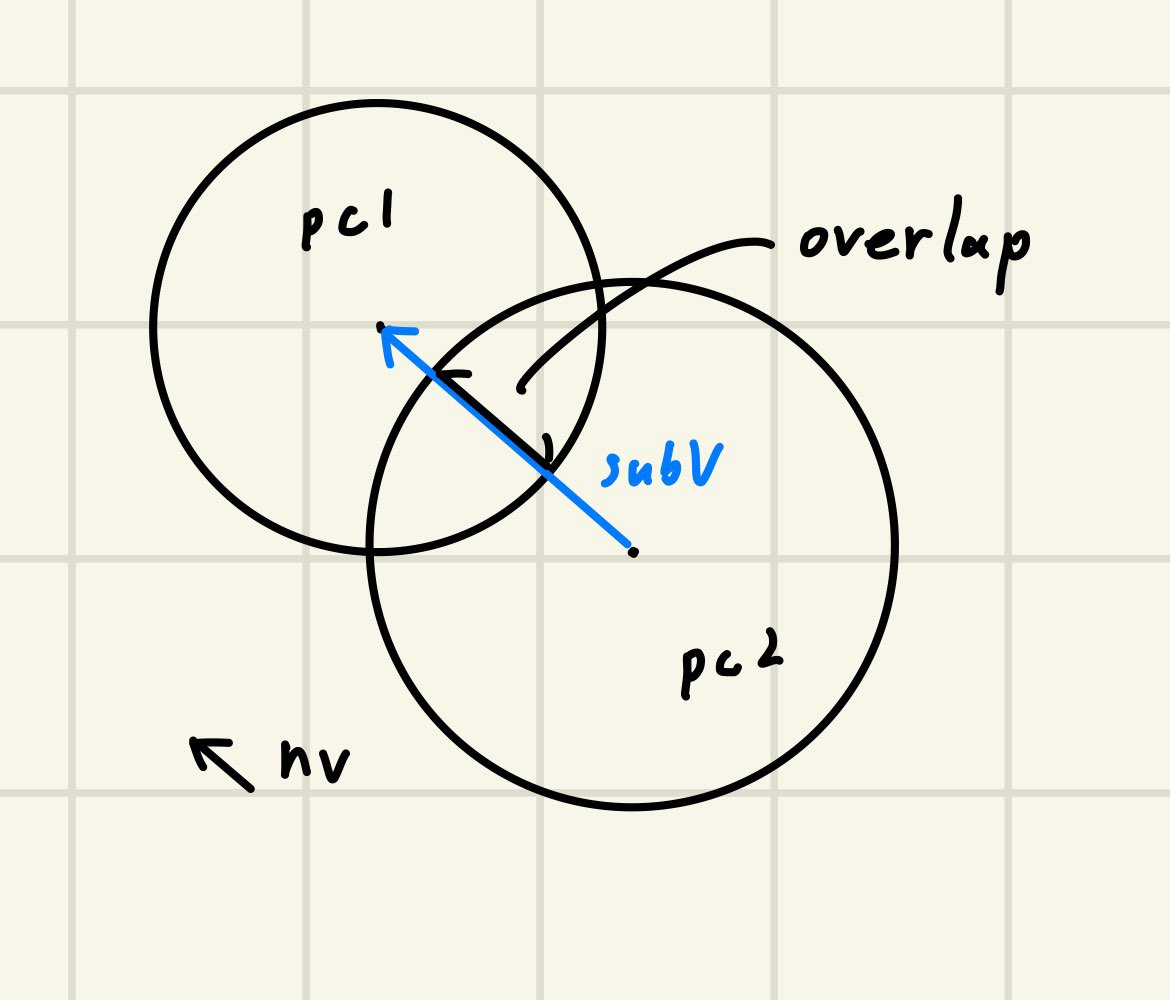
overlapはpc1.r+pc2.r-subV.length()ですね。

3.2垂直抗力

線との衝突同様、反発係数ゼロで考えます。衝突後の速度を$v'$として運動量保存の式を立てると、

m_1v_1+m_2v_2=(m_1+m_2)v'

v'=\frac{m_1v_1+m_2v_2}{m_1+m_2}

v'-v_1=\frac{m_2(v_2-v_1)}{m_1+m_2}

P=m_1(v'-v_1)=\frac{m_1m_2(v_2-v_1)}{m_1+m_2}

垂直抗力の力積$P$が求まりました。各速度は衝突面に垂直な方向の成分であることに注意してください。

3.3摩擦力

先ほど同様衝突点の方向を求めます。

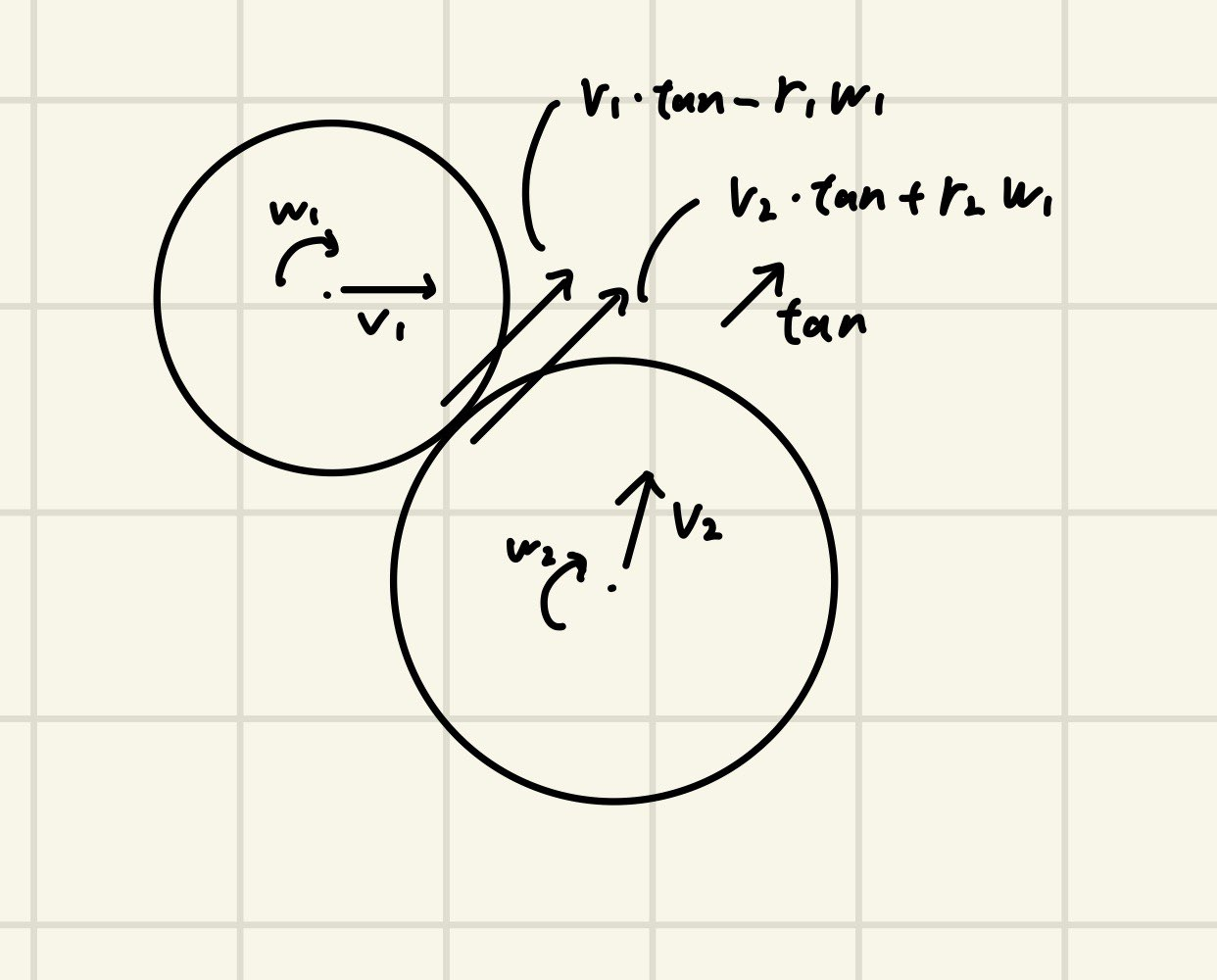
円１は回転成分が負に寄与し、円２は回転成分が正に寄与します。それぞれの衝突点の速さの差をとれば、どちらに擦れているかが分かります。

void Main()
{
	Array<PhysicsCircle> circles;
	Array<Line> walls;

	walls.emplace_back(100, 500, 700, 500);
	walls.emplace_back(100, 700, 100, 100);
	walls.emplace_back(700, 700, 700, 100);

	while (System::Update())
	{
		double delta = Scene::DeltaTime();

		if (MouseL.down()) {
			circles.emplace_back(Cursor::PosF(), Random(10, 100));
		}

		for (auto& o : circles) {
			o.update(delta);
			o.v.y += 9.8 * 60 * delta;//重力
		}
		//Circle と Circle の衝突
		for (auto& pc1 : circles) {
			for (auto& pc2 : circles) {
				Vec2 subV = pc1.pos - pc2.pos;
				if (subV.isZero()) {
					continue;
				}
				double overlap = (pc1.r + pc2.r - subV.length());
				if (overlap < 0) {
					continue;
				}
				Vec2 nv = subV.normalized();
				Vec2 solveV = nv * overlap / 2;
				pc1.pos += solveV;
				pc2.pos -= solveV;
				double dotV = (pc2.v - pc1.v).dot(nv);
				if (dotV < 0) {
					continue;
				}
				Vec2 tan = nv.rotated90();
				Vec2 fDir = -Sign((pc1.v - pc2.v).dot(tan) - pc1.r * pc1.omega - pc2.r * pc2.omega) * tan;
				Vec2 impulse = (nv + fDir * 0.5) * Min(dotV, 50.0) * pc1.M * pc2.M / (pc1.M + pc2.M);
				pc1.addImpulseLocal(impulse, -nv * pc1.r);
				pc2.addImpulseLocal(-impulse, nv * pc2.r);//反作用
			}
		}

		//Circle と wall の衝突
		for (auto& pCircle : circles) {
			for (auto& wall : walls) {
				Vec2 subV = pCircle.pos - wall.closest(pCircle.pos);
				if (subV.isZero()) {
					continue;
				}
				double overlap = (pCircle.r - subV.length());
				if (overlap < 0) {//overlapが正なら衝突
					continue;
				}
				Vec2 nv = subV.normalized();
				pCircle.pos += nv * overlap;//重なり解消
				double dotV = -pCircle.v.dot(nv);//速度の衝突方向成分(衝突に向かう向きを正とする)
				if (dotV < 0) {//衝突方向に向かていないなら無視
					continue;
				}
				Vec2 tan = nv.rotated90();
				Vec2 fDir = -Sign(pCircle.v.dot(tan) - pCircle.r * pCircle.omega) * tan;//摩擦の方向ベクトル
				pCircle.addImpulseLocal((nv + fDir * 0.5) * Min(dotV, 50.0) * pCircle.M, -nv * pCircle.r);//摩擦+垂直効力
			}
		}

		//描画
		for (auto& o : circles) {
			o.draw();
		}
		for (auto& o : walls) {
			o.draw(ColorF(1, 0.5));
		}
	}
}

それぞれ計算式は違いますが、処理はほとんど同じであることが分かると思います。壁との衝突処理を後に行っているのは、描画時により壁に埋まっていない感を演出するためです。

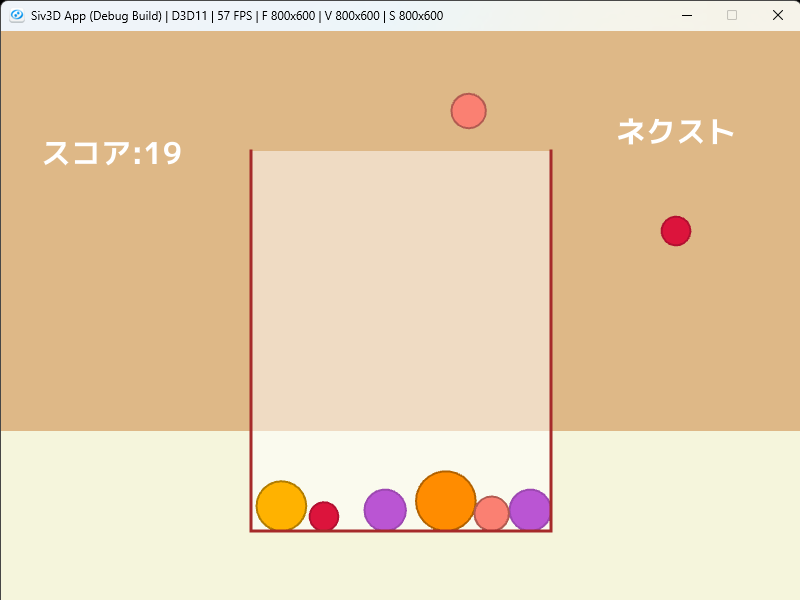
4.残りのスイカゲームを作ります。完成！

あとは好きに実装してください!

• スイカゲームのスコアは階差数列になっているので、$n(n+1)/2$で計算できます。
• 毎回1/200秒の更新をdeltaTimeの分だけする方式に変更しています。
• 衝突判定はいっぱい回せば強くなるので、五回ほど回しています。
• PhisicsCircleを継承したFruitクラスを作り、頻繁に破壊生成がなされるのでスマートポインタを用いて管理しています。
• フルーツの半径は分からなかったので、適当に1.2倍ずつ大きくなるようにしています。
• フルーツはすべて質量１にしています。

# include <Siv3D.hpp> // Siv3D v0.6.12

struct PhysicsCircle {
	Vec2 pos;//重心位置
	Vec2 v;//速度
	double theta;//回転角度
	double omega;//角速度
	double M;//質量
	double I;//慣性モーメント
	double r;//半径

	PhysicsCircle() = default;
	PhysicsCircle(const Vec2& center, double radius) {
		pos = center;
		r = radius;
		v = {};
		theta = 0;
		omega = 0;
		M = 1;
		I = 0.5 * M * r * r;
	}
	Circle circle() const {
		return Circle{ pos,r };
	}
	//重心を基準とした相対座標から力積を加える。
	void addImpulseLocal(const Vec2& impulse, const Vec2& addLocalPos) {
		v += impulse / M;
		omega += addLocalPos.cross(impulse) / I;
	}
	//絶対座標から力積を加える。
	void addImpulse(const Vec2& impulse, const Vec2& addPos) {
		addImpulseLocal(impulse, addPos - pos);
	}
	void update(double delta) {
		pos += v * delta;
		theta += omega * delta;
	}
	void draw(const ColorF& color = Palette::White) {
		circle().draw();
		Line{ pos,Arg::direction = Circular(r,theta).toVec2() }.draw(Palette::Black);
	}
};

Color fruitColor(int32 n) {
	switch (n)
	{
	case 1:
		return Palette::Crimson;
	case 2:
		return Palette::Salmon;
	case 3:
		return Palette::Mediumorchid;
	case 4:
		return Color{ 255, 178, 0 };
	case 5:
		return Palette::Darkorange;
	case 6:
		return Palette::Red;
	case 7:
		return Palette::Khaki;
	case 8:
		return Palette::Pink;
	case 9:
		return Palette::Yellow;
	case 10:
		return Palette::Greenyellow;
	case 11:
		return Palette::Green;
	default:
		return Palette::White;
	}
}

double fruitR(int32 n) {
	return pow(1.2, n) * 12;
}

class Fruit :public PhysicsCircle{
	int32 m_num;
	bool m_dead = false;
	bool m_fallen = false;
public:
	Fruit() = default;
	Fruit(const Vec2& pos, int32 n) :PhysicsCircle({ pos,fruitR(n) }) {
		m_num = n;
	}
	int32 num()const{
		return m_num;
	}
	bool dead() const{
		return m_dead;
	}
	void beDead() {
		m_dead = true;
	}
	bool fallen()const {
		return m_fallen;
	}
	void beFallen() {
		m_fallen = true;
	}
	void draw() const{
		Color c = fruitColor(m_num);
		
		circle().draw(c).drawFrame(2, HSV(c).setV(0.7));
	}
};

void Main()
{
	Scene::SetBackground(Palette::Beige);
	Font font{ FontMethod::MSDF,30,Typeface::Bold };
	Array<std::unique_ptr<Fruit>> circles;
	Array<Line> walls;

	Rect box{ 250,120,300,380 };
	walls.emplace_back(box.bl(), box.br());
	walls.emplace_back(box.bl(), box.tl());
	walls.emplace_back(box.br(), box.tr());

	double accumulatorSec = 0;
	constexpr double stepSec = (1.0 / 200.0);
	constexpr int32 solveNum = 5;

	Vec2 grabPos = { 400 ,80 };
	constexpr double grabSpeed = 150;
	constexpr Vec2 nextPos{ 675,200 };
	std::unique_ptr<Fruit> nextFruit = std::make_unique<Fruit>(nextPos, Random(1, 5));
	std::unique_ptr<Fruit> grabFruit;
	double grabWait = 0.5;

	std::unique_ptr<Fruit> addFruit;

	bool gameOver = false;
	int32 score = 0;

	while (System::Update())
	{
		double delta = Scene::DeltaTime();
		if (not gameOver) {
			if (KeySpace.down() and grabFruit) {
				circles.emplace_back(std::move(grabFruit));
				grabWait = 0;
			}
			if (KeyRight.pressed())grabPos.x += grabSpeed * delta;
			if (KeyLeft.pressed())grabPos.x -= grabSpeed * delta;
			grabPos.x = Clamp(grabPos.x, 250.0, 550.0);
			if (grabFruit) {
				grabPos.x = Clamp(grabPos.x, 250.0 + grabFruit->r, 550.0 - grabFruit->r);
				grabFruit->pos = grabPos;
			}
			else {
				if (grabWait > 0.5) {
					grabFruit = std::move(nextFruit);
					grabFruit->pos = grabPos;
					nextFruit = std::make_unique<Fruit>(nextPos, Random(1, 5));
				}
				grabWait += delta;
			}

			for (accumulatorSec += Scene::DeltaTime(); stepSec <= accumulatorSec; accumulatorSec -= stepSec)
			{
				for (auto& o : circles) {
					o->update(stepSec);
					o->v.y += 9.8 * 60 * stepSec;//重力
				}

				for (auto& i : step(solveNum)) {
					//Circle と Circle の衝突
					for (auto& pc1 : circles) {
						for (auto& pc2 : circles) {
							Vec2 subV = pc1->pos - pc2->pos;
							if (subV.isZero()) {
								continue;
							}
							double overlap = (pc1->r + pc2->r - subV.length());
							if (overlap < 0) {
								continue;
							}
							Vec2 nv = subV.normalized();
							Vec2 solveV = nv * overlap / 2;
							pc1->pos += solveV;
							pc2->pos -= solveV;

							//スイカゲームの処理
							pc1->beFallen();
							pc2->beFallen();
							if (pc1->num() == pc2->num() and not addFruit) {
								pc1->beDead();
								pc2->beDead();
								if (pc1->num() <= 10)addFruit = std::make_unique<Fruit>(pc1->pos - nv * pc1->r, pc1->num() + 1);
								score += pc1->num() * (pc1->num() + 1) / 2;
							}


							double dotV = (pc2->v - pc1->v).dot(nv);
							if (dotV < 0) {
								continue;
							}
							Vec2 tan = nv.rotated90();
							Vec2 fDir = -Sign((pc1->v - pc2->v).dot(tan) - pc1->r * pc1->omega - pc2->r * pc2->omega) * tan;
							Vec2 impulse = (nv + fDir * 0.5) * Min(dotV, 50.0) * pc1->M * pc2->M / (pc1->M + pc2->M);
							pc1->addImpulseLocal(impulse, -nv * pc1->r);
							pc2->addImpulseLocal(-impulse, nv * pc2->r);//反作用
						}
					}

					//Circle と wall の衝突
					for (auto& pCircle : circles) {
						for (auto& wall : walls) {
							Vec2 subV = pCircle->pos - wall.closest(pCircle->pos);
							if (subV.isZero()) {
								continue;
							}
							double overlap = (pCircle->r - subV.length());
							if (overlap < 0) {//overlapが正なら衝突
								continue;
							}
							pCircle->beFallen();//スイカゲームの処理
							Vec2 nv = subV.normalized();
							pCircle->pos += nv * overlap;//重なり解消
							double dotV = -pCircle->v.dot(nv);//速度の衝突方向成分(衝突に向かう向きを正とする)
							if (dotV < 0) {//衝突方向に向かていないなら無視
								continue;
							}
							Vec2 tan = nv.rotated90();
							Vec2 fDir = -Sign(pCircle->v.dot(tan) - pCircle->r * pCircle->omega) * tan;//摩擦の方向ベクトル
							pCircle->addImpulseLocal((nv + fDir * 0.5) * Min(dotV, 50.0) * pCircle->M, -nv * pCircle->r);//摩擦+垂直効力
						}
					}


					circles.remove_if([](const auto& o) {return o->dead(); });
					if (addFruit)circles.emplace_back(std::move(addFruit));
				}
			}

			for (auto& o : circles) {
				if (o->fallen() and o->pos.y - o->r < 80 or o->pos.y>800) {
					gameOver = true;
				}
			}
		}
		else {
			if (KeyEnter.down()) {
				circles.clear();
				grabFruit.reset();
				nextFruit = std::make_unique<Fruit>(nextPos, Random(1, 5));
				grabWait = 0.5;
				grabPos = { 400,80 };
				gameOver = false;
				score = 0;
			}
		}
		
		//描画
		Rect{ 800,400 }.draw(Palette::Burlywood);
		box.draw(ColorF(1, 0.5));
		for (auto& o : circles) {
			o->draw();
		}
		for (auto& o : walls) {
			o.draw(3,Palette::Brown);
		}
		Circle{ grabPos,10 }.draw();
		if(grabFruit)grabFruit->draw();
		if (nextFruit)nextFruit->draw();

		font(U"スコア:", score).draw(30, 40, 100);
		font(U"ネクスト").drawAt(30, nextPos.x,nextPos.y-100);
		if (gameOver) {
			Scene::Rect().draw(ColorF(0, 0.5));
			font(U"スコア:", score).drawAt(60, 400, 300);
			font(U"Enterでリスタート", score).drawAt(40, 400, 500);

		}
	}
}

5.課題

壁を線で実装したために、割とよく貫通します。ぜひ問題を解決してみてください。