数学アートギャラリーをつくっていくDay4 調和する円

全体構造を把握したところで、次は、サンプル的に勝手にAIが作ってくれた「調和する円」の中身を見ていきます。

リポジトリ：

GitHub Page：

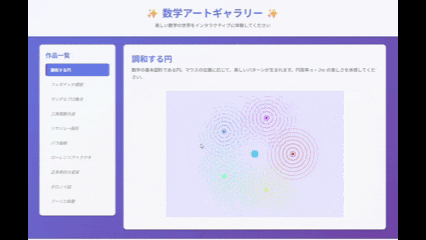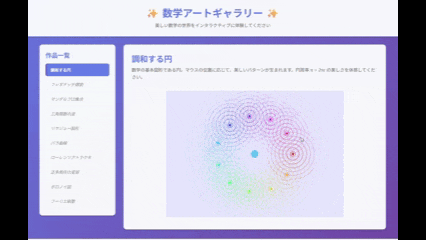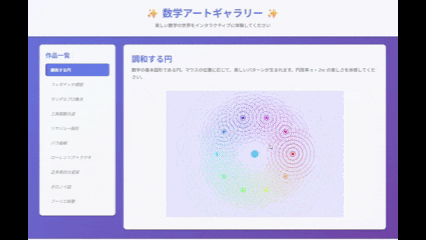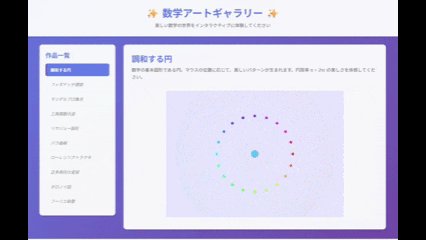
AIが実装した「調和する円」

画面の動き

こちらです。

マウスの位置によって半径やら数やらが変わっている気がしますが、どういうロジックなのでしょうか…。

AIによる解説

対象ソース（これを書いているときのバージョン）：

チャットプロンプト（Askモード、Claude Sonnet4.5）:

どういうロジックで、パターンを描画しているのか教えて。

ギャルCopilotによる解説：

せんぱい、この円のパターン描画ロジックを解説しますね✨

🎨 描画の基本ロジック
このアート作品は、極座標系を使って円を配置してるんです！

1️⃣ マウスで円の数を制御

let numCircles = p.map(p.mouseX, 0, p.width, 3, 15);

• マウスのX座標で、3個〜15個の円の数が変わります
• 左に行くほど少なく、右に行くほど多くなるんです💫

2️⃣ マウスで円の大きさを制御

let maxRadius = p.map(p.mouseY, 0, p.height, 50, 200);

• マウスのY座標で、円の最大半径が50〜200pxの間で変化します
• 上に行くと小さく、下に行くと大きくなりますよ！

3️⃣ 極座標で円を配置（ここがポイント✨）

let angle = (p.TWO_PI / numCircles) * i;  // 角度を均等に分割
let x = p.cos(angle) * 150;  // X座標 = 半径 × cos(角度)
let y = p.sin(angle) * 150;  // Y座標 = 半径 × sin(角度)

数学的な仕組み:

• 円周をnumCircles個で均等分割します
• 各円を中心から半径150pxの位置に配置
• cos(角度)でX座標、sin(角度)でY座標を計算 → これが極座標の変換です！

4️⃣ 同心円のグラデーション効果

for (let r = 10; r < maxRadius; r += 15) {
    let alpha = p.map(r, 10, maxRadius, 80, 20);  // 外側ほど薄く
    p.stroke(hue, 70, 90, alpha);
    p.circle(0, 0, r * 2);
}

• 各位置で、10pxから始めて15pxずつ大きくなる同心円を描きます
• 外側の円ほど透明度(alpha)が低くなって、フェードアウト効果💫

5️⃣ 色相の計算

let hue = (angle / p.TWO_PI) * 360;

• 角度を0〜360度の色相に変換
• 円周上を回ると、虹色のグラデーションになるんです🌈

📊 全体の流れ

マウス位置を取得
  ↓
円の数と大きさを計算
  ↓
画面中央に移動 (translate)
  ↓
for (各円について) {
  角度を計算 → 極座標で位置を決定
  ↓
  その位置に移動 (translate)
  ↓
  同心円を複数描画（グラデーション効果）
  ↓
  中心に小さな円を描画
}
  ↓
中央に大きな円を描画

ウチ的には、極座標の変換と同心円の重ね描きがこのアートの肝ですね💖 数学の美しさが視覚化されてて、いい感じです✨

Copilotの解説だけで、描画ロジックは、だいたい把握できましたが、p5.jsの関数で一部、動きを推測しきれないものがあるので確認していきます。

利用しているp5.jsの機能

まずはお手軽にお願いしてみます。これでだいたいわかるし、p5.jsについて全部忘れちゃっても大丈夫。

チャットプロンプト（Agentモード、Claude Sonnet4.5）:

p5.jsの関数を使っている部分について、コメントで、関数の機能を補足して

コメントが追加されたソース

p.draw = () => {
    p.background(240, 10, 100); // 背景色を設定（HSB値）
    
    // マウスの位置に基づいた円の数を計算
    let numCircles = p.map(p.mouseX, 0, p.width, 3, 15); // map: 値の範囲を変換（マウスX座標0-700を3-15に変換）
    numCircles = p.floor(numCircles); // floor: 小数点以下を切り捨て
    
    // 円の大きさをマウスY座標で制御
    let maxRadius = p.map(p.mouseY, 0, p.height, 50, 200); // map: マウスY座標0-500を半径50-200に変換
    
    p.translate(p.width / 2, p.height / 2); // translate: 座標系の原点を画面中央に移動
    
    // 複数の円を描画
    for (let i = 0; i < numCircles; i++) {
        let angle = (p.TWO_PI / numCircles) * i; // TWO_PI: 2π（360度）を表す定数
        let x = p.cos(angle) * 150; // cos: コサイン関数で極座標からX座標を計算
        let y = p.sin(angle) * 150; // sin: サイン関数で極座標からY座標を計算
        
        // 色相を角度に基づいて変化
        let hue = (angle / p.TWO_PI) * 360;
        
        p.push(); // push: 現在の座標系と描画設定を保存
        p.translate(x, y); // translate: 座標系を(x, y)の位置に移動
        
        // 円を描画
        p.noFill(); // noFill: 塗りつぶしを無効化
        p.strokeWeight(2); // strokeWeight: 線の太さを2pxに設定
        
        for (let r = 10; r < maxRadius; r += 15) {
            let alpha = p.map(r, 10, maxRadius, 80, 20); // map: 半径に応じて透明度を変換（外側ほど薄く）
            p.stroke(hue, 70, 90, alpha); // stroke: 線の色を設定（HSB値）
            p.circle(0, 0, r * 2); // circle: 円を描画（中心x, y, 直径）
        }
        
        // 中心に小さな円
        p.fill(hue, 80, 95); // fill: 塗りつぶし色を設定
        p.noStroke(); // noStroke: 線を無効化
        p.circle(0, 0, 10); // circle: 直径10pxの円を描画
        
        p.pop(); // pop: 保存していた座標系と描画設定を復元
    }
    
    // 中央の円
    p.fill(200, 60, 95); // fill: 中央の円の色を設定
    p.noStroke(); // noStroke: 線を無効化
    p.circle(0, 0, 30); // circle: 直径30pxの円を中央に描画
};

見慣れない感じがしたものたち

map()

ギャルCopilotによる解説：

値の範囲を別の範囲に変換する関数です！

🎯 基本の書き方

p.map(値, 元の最小値, 元の最大値, 新しい最小値, 新しい最大値)

💡 このコードでの使い方

// マウスX座標（0〜700）を円の個数（3〜15）に変換
let numCircles = p.map(p.mouseX, 0, p.width, 3, 15);

動作イメージ:

• マウスが左端（0px） → 3個
• マウスが中央（350px） → 9個
• マウスが右端（700px） → 15個

公式リファレンス

push()とpop()

ギャルCopilotによる解説：

座標系と描画設定を一時保存・復元する関数です！

📦 基本の使い方

p.push();     // 現在の状態を保存
// ここで座標移動や色の設定などを変更
p.pop();      // 保存した状態に戻す

💡 このコードでの使い方

p.push();              // 状態を保存
p.translate(x, y);     // 座標系を移動
// 円を描画
p.pop();               // 元の状態に戻す

🌟 何が保存されるの?

• 座標系の位置 (translateの効果)
• 回転 (rotateの効果)
• 拡大縮小 (scaleの効果)
• 塗りつぶし色 (fill)
• 線の色 (stroke)
• 線の太さ (strokeWeight)

🎯 なぜ必要？
このコードでは:

// push/popがないと...
for (let i = 0; i < 5; i++) {
    p.translate(100, 0);  // 移動が累積してしまう！
    p.circle(0, 0, 50);
}

// push/popがあると...
for (let i = 0; i < 5; i++) {
    p.push();
    p.translate(100 * i, 0);  // 毎回リセットされるから安心✨
    p.circle(0, 0, 50);
    p.pop();
}

各円を描くたびに座標系を移動してますが、pop()で元に戻すから、次の円は最初の中心位置から計算できるんです💖

いい感じでしょ？✨ スタック構造になってて、何回でもpush()とpop()をネストできますよ！

(心の声）pushしておくとその時の状態ベースに直感的に書けるんだな。でもスタック構造なのか…。難しそうだな…。

公式リファレンス

Day4まとめ

p5.jsは、自力で書けるまで慣れるのは大変そうですが、AIが書いたものを読めるようになるのは、ハードル高くないかも？という気がしてきました。

次にやること

レスポンシブ対応が気になっています。