今日は、「人間の脳の働き (神経細胞間の情報ネットワーク) を模したシステムを作りたい」という「 ニューラルネットワーク 」の 入門の入門 についてお話しします。
人間の脳では、何百億個という ニューロン (神経細胞) が情報をやりとりしています。
ニューロンによる情報伝達は、主に電気信号によるものです。一方でコンピュータも電気信号で情報伝達の処理を行っています。
ということで、コンピュータ上で、 脳内で起きている情報処理を真似できないか、という発想になります。
なので、この記事では、まずは、実際の人間の脳がどのように情報の伝達をしているのか という解説から入り、 生体ニューロン と 形式ニューロン のお話までします。
数式などは出てきません。(数式とかが出て来る段階の内容は別の記事で書きます。この記事は、その前段階までの解説です。)
(↑この写真は Adobe Stock でライセンス購入したものにコメントを書き加えたものです)
キーワード
- ニューロン(神経細胞)
- シナプス
- ニューラルネットワーク
- ヘッブ則
- 生体ニューロン と 形式ニューロン
- 全か無かの法則
- 刺激の強さの 閾値 (いきち/しきいち)
前回の記事:「 『イラストで読む AI 入門』読書メモ 01 : AI ブームの歴史 (パーセプトロン, バックプロパゲーション, ディープラーニング) 」
前置き
この記事は、森川 幸人 さんの著書『イラストで読むAI入門』を私が読んだ時の読書メモです。
読んで学んだことを皆様にもシェアできたら嬉しいと思い、自分で調べた情報もたくさん添えながら、読書メモをこちらにまとめています。この記事は、その読書メモ記事群の第2回目です。
お礼
先月書きました前回の記事 (私の Qiita 初記事) が、
380 いいね超え、15000 PV を頂きました。トレンド入りもしました。
読んで頂けて嬉しいです。ありがとうございます!
ヒトの脳について
人工ニューラルネットワークの話の前に、まず、私たちヒトの脳について。
私たちの脳がどうやって体に情報を伝えているのかについてのお話です。高校生物の内容です。
人間の脳では、何百億個という ニューロン (神経細胞) が、
相互に連結して神経回路をつくり、
電気信号によって情報をやりとりしています。
ひとつの ニューロン (神経細胞) は、脳の中で情報を受け取り、
シナプス を通して次のニューロンや筋肉などの器官に伝えるはたらきをしています。
(ちなみに、こころの病気の時は、この神経細胞の信号がうまく伝わっていないことが分かっています。)
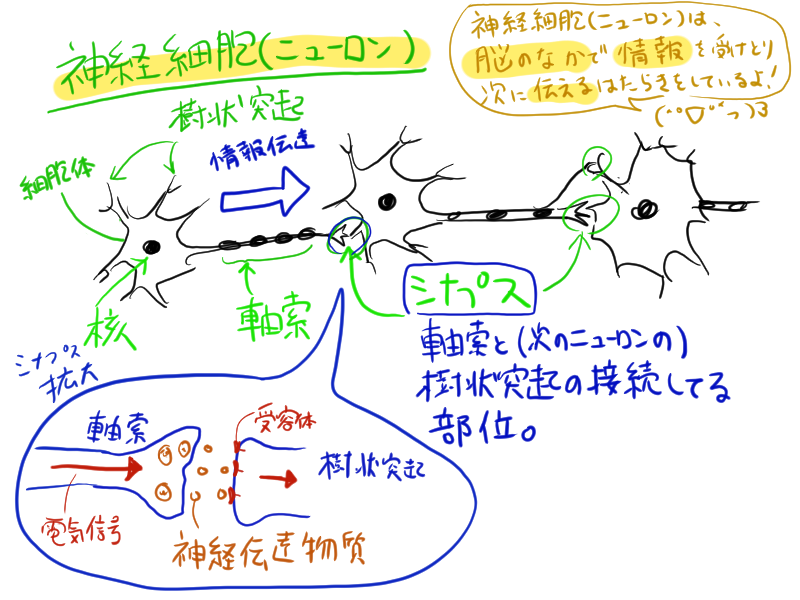
神経細胞同士の情報のやり取りの図を描いてみました。(私は副業で漫画家やってるけど細胞の絵は得意ではないことが分かりました)
これらについて説明していきます。
神経細胞 (ニューロン)
情報はどうやって伝わるのかというと、まず、脳にあるたくさんの ニューロン と呼ばれる神経細胞が、次の細胞や器官に情報を伝えてくれます。
人間の脳にはこのニューロンが何百億個もあるといわれています。
構造 (上の絵を参照しながら):
- 細胞体 - ニューロンの中心であり、核やミトコンドリアや中心体などを含んでいる部分
- 樹状突起 (じゅじょうとっき) - 細胞体の表面にある数十の突起
- 核
- 軸索 (じくさく) - 細胞体から長く伸びた1本の突起
- 髄鞘 (ずいしょう) - 軸索の回りの太くなっているところ。また、髄鞘の切れ目を「ランビエ絞輪(こうりん)」という
- シナプス - ニューロンの軸索の末端から、次のニューロンや効果器(筋肉など)への接続部分。ここで情報伝達物質がやり取りされてる。 記憶や学習によってシナプスの結合度は変化する とされている(重要!!!!)。また、ここシナプスでは、たんに情報を伝えるだけでなく、情報の重みづけ の処理も行っている。(重みづけについては後の記事で解説)
シナプスと次の神経細胞の間には「シナプス間隙 (かんげき)」と呼ばれる小さな隙間があり、直接つながっていません。(図に書いた拡大図のあたり)
そのため、神経細胞は次の神経細胞に直接電気信号を伝えることはしておらず、シナプスから放出される 神経伝達物質 を放出し、
この神経伝達物質が次の神経細胞を刺激することで、次の神経細胞に信号を伝えています。
全か無かの法則
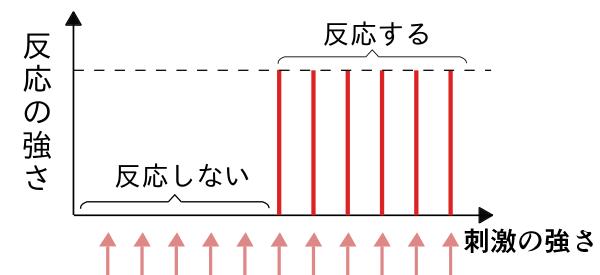
刺激の強さと反応の大きさに関する法則。
↑ ポイントは、棒グラフの長さが長くなったり短くなったりしてなくて、閾値後に一定になってる こと
(図:高等学校生物/生物I/環境と動物の反応 | Wikibooks)
1本のニューロンは、刺激の強さが一定値より弱いと興奮しない。この、さかいめの一定値を 閾値 (いきち/しきいち)という。
閾値以上だとニューロンは興奮し、その興奮の大きさは刺激の強さによらず一定であり、活動電位の大きさは一定である。
ニューロンは、刺激に対して、興奮するか、興奮しないか、のどちらか2通りだけである。
ニューロンの、このような反応の現れ方を 全か無かの法則 (all-or-none law)と呼ぶ。
(高等学校生物/生物I/環境と動物の反応 | Wikibooks より引用)
要するにひとつのニューロンに対する刺激の「反応の大きさ」とかは無くて、「興奮したかしてないか」のふたつの状態 しか取り得ない。
とても単純だね! 0 か 1 的な。
ちなみに、興奮の「頻度」(回数の度合い)が高くなることで「刺激の強さ」は感じることができる
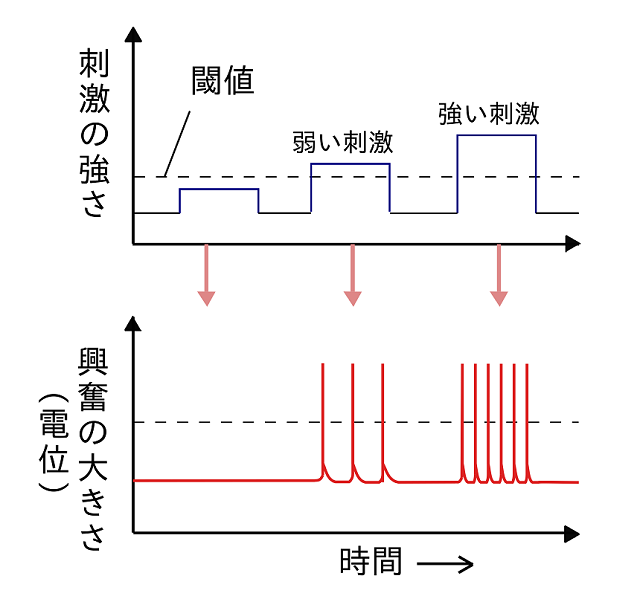
(図:高等学校生物/生物I/環境と動物の反応 | Wikibooks)
上の『刺激の強さと興奮の頻度』の図から、電位は一定だけど、頻度が高くなることで、強い刺激を感じているのが分かる。
余談
余談ですが、みんな大好き絵素材屋の『いらすとや』にニューロンの絵があって、どんだけ守備範囲広いんだと驚きました。すごすぎ。
↑『脳内で情報を伝達や記憶する役割を果たす神経細胞のイラスト』by いらすとや
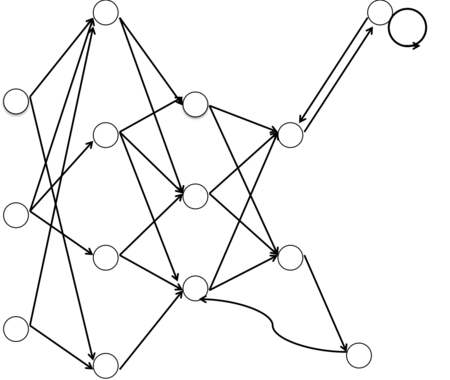
ニューラルネットワーク
↑ 相互作用ニューラルネットワークモデル
(図: ニューラルネットワーク - Wikipedia より)
現在、第三次 AI ブームが来てるけど、
その火付け役になったのは ディープラーニング ( 深層学習 ) だという話を
前回の記事でお話ししました
で。
さて、ディープラーニングを含め、ここまで説明してきたのは、いずれも脳をモデルにした「 ニューラルネットワーク 」というモデルです。
(『イラストで読むAI入門』 40 ページより)
脳は非常に高い情報処理能力を持っていますが、その働きをコンピュータを使い模倣しようというこころみが行われてきました。
ニューラルネットワーク とは、人間の脳の仕組み(脳の神経細胞(ニューロン)により構成される情報のネットワーク)をモデル化したものです。
昔、だんだん脳の構造が明らかになってきたあたり、ひとつひとつの細胞は実は単純な動きしかしていないことが分かってきました。
神経細胞同士は連結していて、前の細胞から電気信号を受け取ったら、その量に応じて、興奮するか、しないかでいるかどちらかの状態である。( 全か無かの法則 )
ニューラルネットワークは、脳の細胞に関する「 ヘッブ則 」という仮説を基盤に発展してきたものです。
(『イラストで読むAI入門』 40 ページより)
ヘッブ則
(↑ Donald Hebb 氏の画像:Cambridge Medical Journal より)
ヘッブ則 ( ヘブ則 ) は、1949年カナダの心理学者であった Donald Hebb が自らの著書『The Organization of Behavior』の中で唱えた仮説で
"When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased."
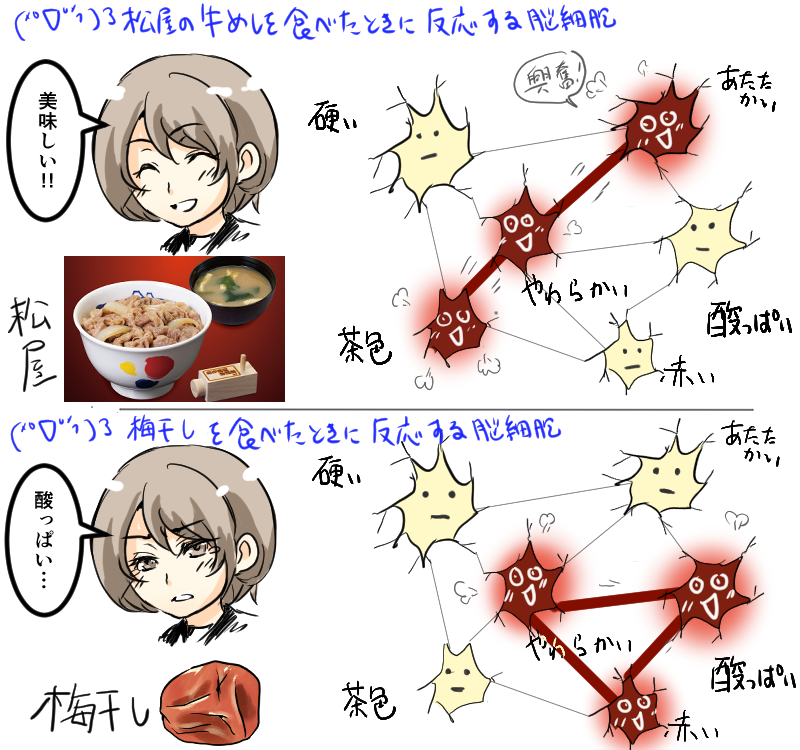
ようするに「 同時に発火したニューロン間のシナプス結合は強められる 」ということを言っています。
脳細胞はいろいろな脳細胞と連結しています。たとえば、「梅干し」を食べたとします。すると「赤い」ものに反応する脳細胞、「丸い」ものに反応する脳細胞、「酸っぱい」に反応する脳細胞が 同時に興奮 します。
この時、同時に反応した脳細胞同士の結合が強まり、逆に反応しなかった脳細胞の結合は弱くなります。 興奮した脳細胞同士の結合が強く太くなり、相反する脳細胞の結合は弱くなる のではないかというのがヘッブの仮説です。
「 何かをしたときに同時に興奮した細胞同士の結合は太くなるのではないか 」と考えたわけですね。
(引用:『イラストで読むAI入門』 42ページ目)
↓ 同時に興奮したニューロン間のシナプス結合が強まってる図
(上の松屋のプレミアム牛めしの写真はこちらから→ 松屋公式サイト)
(こんなに真面目に梅干しを描いたのは初めてです)
当時は MRI も無く、実際にはっきりと検証されたわけでもないのだけれど、
このヘッブの論文を読んだローゼンバッハが「それだったら数理モデルになるのでは?」と考え、コンピュータでプログラム実験してみたところ、
実際に簡単な記憶や判断ができて、がぜん盛り上がりました。
興奮したもの同士がたくさん信号を送りあうという、このヘッブの仮説の上の脳のモデルを模倣したところから、ニューラルネットワークは始まりました。
生体ニューロンのモデル化
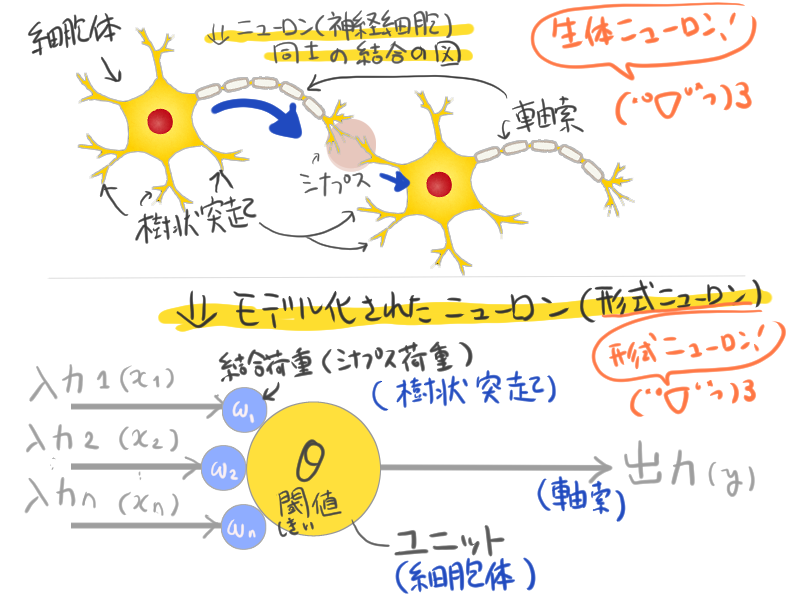
で、ニューラルネットワークを考えるにあたり、いちいちニューロンを描くのは大変なので、モデル化された書き方があります。
モデル化されたニューロンは「形式ニューロン」と呼ばれます。
↓ 書いた。上が生体ニューロン、下が形式ニューロン
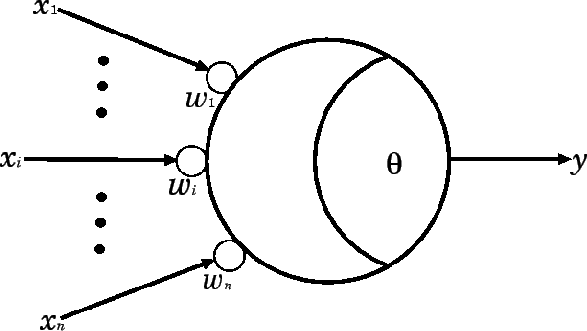
- 結合荷重 (connection weight)。「 重み 」や「 シナプス荷重 」とも呼ぶ。生体ニューロンの 樹状突起 (じゅじょうとっき)に相当する。ここには任意の実数値を入れる。これはシナプスが異なる伝達効率を持っている事を表すため。
- ユニット。「 ノード 」とも呼ぶ。生体ニューロンの 細胞体 に相当する。ニューロンの信号伝達のように 閾値 (いきち/しきいち)を計算するための部分。入力に結合荷重の重みをかけた総和が 閾値 を超えたかどうか判断し、超えたら"1"、超えなかったら"0"を返す。(『全か無かの法則』の節で出てきましたね!)
(解説文引用:『パーセプトロンとは?』1-3 より)
生体ニューロンがうまくモデル化されててすごい!
これなら数値計算しやすそうですね。
(ニューロンモデル図:gifu-nct.ac.jp より)
これでこの形式ニューロンのノードの図を使ってネットワーク図を描いていけそうです。
ニューラルネットワーク
前述の通り、人間の脳では、何百億個のニューロンが互いに繋がり、巨大なシステムをつくっています。
上記のニューロンモデルをいくつも繋げてニューラルネットワークを作ることが出来ます。(この辺の詳細は長くなるので別の記事に書きます。)
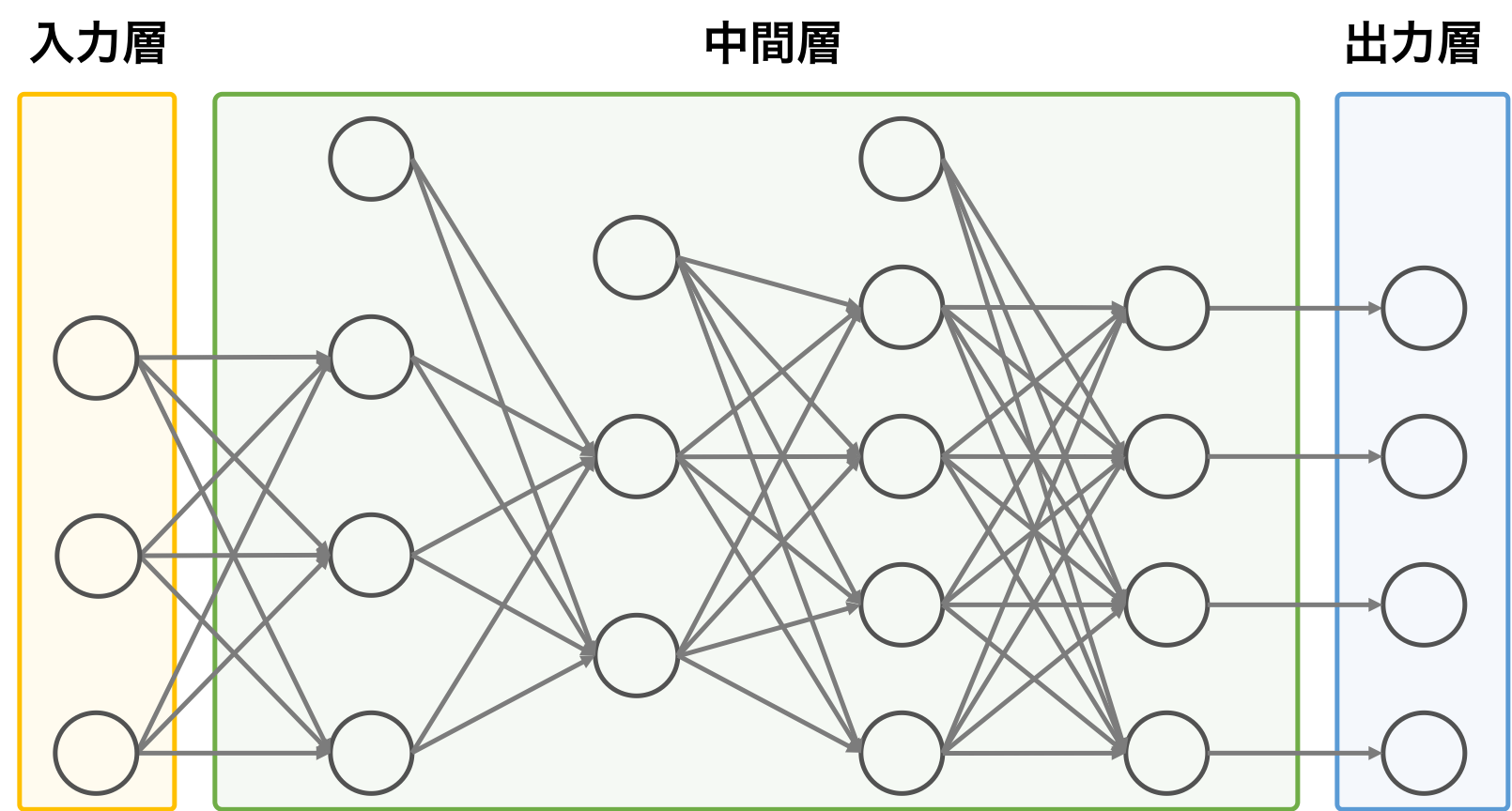
ニューラルネットワークの基本構造は3種類の「層」に分かれます。
- 入力層
- 中間層 (隠れ層)
- 出力層
(図:algorithm.joho.info より)
この中間層の層の数を増やすことによって ディープラーニング が実現されています↓
(図:axa.biopapyrus.jp より)
この辺のことは長くなるので別の記事で書きます。取り急ぎ用語だけ。
まとめ
- ヒトの脳内では、何百億個もの ニューロン (神経細胞) 同士が情報のやり取りをしている
- コンピュータ上で神経回路を模してつくられたシステム を「(人工) ニューラルネットワーク 」と呼ぶ。
- 人間の脳内で、 ニューロン (神経細胞) 同士は シナプス でつながっており、シナプスでは 学習によって情報の「重みづけ」 を行いながら次のニューロンに情報を伝えている。
- 記憶や学習によってシナプスの結合度は変化する
- 学習によって神経回路のつなぎかえが起こる
- 『 全か無かの法則 』1本のニューロンは、刺激の強さが一定値より弱いと興奮しない。ニューロンは、刺激に対して、興奮するか、興奮しないか、のどちらか2通りだけ、という法則。また、この、刺激のさかいめの一定値を 閾値(いきち/しきいち)という。
- 『 ヘッブ則』。ニューラルネットワークの基礎となる考え方で「 何かをしたときに同時に興奮したニューロン同士の結合は太くなる 」という法則
- 生体ニューロン のモデル化したものを『 形式ニューロン』または『 人工ニューロン』という。
感想
情報技術について勉強してると思ったら、気づいたら高校生物の教科書や別冊ニュートンを読んでいました。楽しい!
まだまだ勉強することがたくさんなので楽しいです。
長い記事(私の勉強メモ)を読んでくださりありがとうございました! 次回もまた学んだことを書きます!
参考文献・参考記事
- 『イラストで読むAI入門』| 森川 幸人 さんの著書。良書だと思ったので今ここで読書メモを書き始めた。
- 『Microsoft Azure Machine Learning とは』 | Azure Machine Learning とは、機械学習モデルのトレーニング、デプロイ、自動化、管理を行うためのクラウド サービスであり、これらの操作のすべてをクラウドによって提供される幅広い規模で行うことができます。
- 『Azure Machine Learning Studio のアルゴリズムの選択方法』|これすごい。いっかい読んで欲しい。分かりやすい
- 『機械学習の重要な用語の用語集』 | 精度, 曲線下面積 (AUC), 二項分類, F 値, ハイパーパラメーター, 教師あり機械学習,再現率, 正則化, 回帰, 相対絶対誤差, など
- 『がんばれ森川くんの遺伝子くん』 | 著者の森川先生による記事
- 『ニューロン』 | 中外製薬株式会社による記事
- 『ニューラルネットワーク初歩をまとめ - 元ダメ院生がギークになるまで続ける日記』|
- 『ニューラルネットワーク - 農業情報』 | サイト名がまさかの『農業情報』なんだけど、農業だけでなく深層学習がすごい勉強になる
- 『初心者の初心者による初心者のためのニューラルネットワーク#1〜理論:順伝播編〜』
- 『パーセプトロンとは?』
- 『ニュートン別冊 ゼロからわかる人工知能』(2018年5月10日)|Kindle 版で読んだ