Diagnosing Bottlenecks in Deep Q-Learning Algorithms 論文まとめ

この記事の内容・目的

基本的にはDiagnosing Bottlenecks in Deep Q-Learning Algorithmsの直訳をベースにまとめていきます。
直訳は「である調」、私のコメントは「ですます調」で書くつもりですが、ところどころ違うかもしれません。
目的は自身の理解のためがメインですが、英語で読むのが面倒な方の参考になればいいなと思っています。
強化学習についての基本的な事項を理解している方向けの記事になりますので、強化学習に関する基本的な用語の説明はありません。ご了承ください。

※後ほど訂正・補足を追加していく予定です。

超速まとめ

問題意識：DQNの挙動は理論的にも経験的にも今まで十分に理解されていなかった
目的：実験的に様々なQ-Learningのトピックを解析して、より良いアルゴリズムの開発の方向性を示す
手法：Q-value等のほとんど正しい答え(oracle value,oracle solution,...)がわかっているような環境のなかで、Q-Learningアルゴリズムを少しずつ変化させた時に、リターン値等のパフォーマンスの変化を解析した。(この手法を'unit testing'と表現しています)
結果
- 大きい関数近似器による悪影響は、小さい関数近似器を用いることによる悪影響より小さく、様々な点で大きい関数近似器を用いることが推奨される
- early stopping と replay bufferは過学習に効く
- AFMというサンプリング手法は従来の手法よりも良い結果を出せる
  - 特に、問題に対して関数近似器が小さい時にも良いパフォーマンスを維持できる

個人的に思ったこと

嬉しいこと
- 大きい関数近似器を用いることの有用性が支持され、実際に深層強化学習(ここでは関数近似器にニューラルネットを使う強化学習と言う意味です)を実装する時に、モデルサイズを比較考慮する軸ができた。
- 具体的に実行することができる改善策の案(early stopping,replay buffer,AFM)が提示されているので、従来よりも学習を安定させることができそう。
  - early stoppingはハイパラ設定があるのでちょっと工夫が必要
疑問点
- 調整されていない環境・条件下でどこまで適用することができるのか
- 状態空間が巨大な時にどうすれば良いのか
  - 状態空間のスケールと関数近似器の表現力の比率で何か言えたりしそう？
    - 妄想：|$ \mathcal{S} $| $ = N$の時に、関数近似器の表現力を|$d$|とすると、関数近似誤差が確率$1-\delta$で$N$と $d$ に依存した多項式で抑えられる、みたいなことが言えたりしたら嬉しい。

Abstract

Q-learningアルゴリズムは、高次元な状態・行動を扱う関数近似の手法として、強化学習でよく使われる。だが、関数近似を伴うQ-Learningアルゴリズムの挙動は理論的にも経験的にも十分に理解されていないのが現状である。
そこで本研究では、'unit testing'のフレームワークを用いて、Q-Learningの潜在的な問題を経験的に調査した。特に関数近似に関連した問題である、サンプリングエラーや非定常性、いつ使うことができるかという点を重点的に調査した。
結果として以下のような発見が得られた。
- 巨大なニューラルネットワークの構造が学習の安定性に寄与すること
- 過学習を避けるための実践的な対策
- 関数近似誤差を補償するような新しいサンプリング手法

Introduction

Q-Learningは以下のような利点があり、人気の手法である。
- サンプル効率が良い
- 実装がシンプルである
しかし、テーブル形式の標準的なQ-Learningは収束性を持ち、理論的な解析も行われているが、ニューラルネットワークのような非線形な関数近似を用いたQ-Learningの挙動は十分に理解されていない。
そこで本研究では、oracle solversを利用し、Q-functionとその分布のground truthを得ることができる'unit testing'フレームワークを用いて、Q-Learningを経験的に解析した。
本研究では以下の4つの疑問を調査した。

1. 収束性において、関数近似はどのような影響があるのか？

Q-Learningでの関数近似の影響を見るために、異なる表現力を持った関数近似器を用意し、それらの関数近似器の得た結果と最適Q-function,最適射影Q-functionによって得られた解と比較・解析を行った。
驚くべきことに、関数近似誤差は、関数近似器の表現力が高い時だけ問題になることが明らかになった。これは表現力の高い関数近似器はbacked-up Q-functionのほぼ完璧な射影になりうることから解釈でき、不完全なl2ノルム射影による収束性の問題を緩和することができると言える。

2. サンプリングエラーと過学習はどのような影響があるのか？

Q-Learningは状態遷移確率が明らかでないマルコフ決定過程(MDP)を解く際に用いられることが多く、環境から経験をサンプリングして学習する必要がある。これはサンプリングエラー、過学習に導くという問題がある。
本研究では実際に過学習が存在することを、gradient steps(サンプルあたりのパラメータ更新回数)に関する調査から明らかにし、early stoppingが学習パフォーマンスを向上させる有効なテクニックであることを示す。
具体的には、本研究では過学習の程度を、複数の評価指標を用いて定量的に評価し、過学習を緩和させるためのいくつかの方法に対して調査を行なった。

3. 分布シフトとターゲットの移動はどのような影響があるのか？

(What is the effect of distribution shift and a moving target? )

標準的なQ-Learningでは特定の損失関数に基づく最適化を行わないため、以下の二つの点から非定常的な学習になってしまう。
- 目標の値が学習中も更新される(moving target)
- 異なる方策から得られた経験を利用するので、ベルマンエラーの下での分布が変化する(distribution shift)
本研究ではdistribution shiftとmoving targetによる非定常性を定量的に評価する指標を提案する。驚くべきことに、調整された実験環境において、distribution shiftとmoving targetはパフォーマンスの低下と関連していないことがわかり大きなdistribution shiftを伴ったサンプリング戦略は非常に良いパフォーマンスを発揮した。

4. 最良なサンプリング・重み付き分布は何か？

上記のdistribution shiftと深く関連した問題として、どの分布から経験をサンプリングするか、といった問題がある。既往研究では、on-policy samplesはoff-policyのものよりも優れており、on-policy型のアルゴリズムは収束に関する望ましい性質を持つことが理論的に示されている。
しかし、では実際にどのような分布を選ぶことが良い学習につながるのか、といった理論的な研究は少なく、本研究ではサンプリング分布の選び方に関しても調査を行なった。
驚くべきことに、on-policy型の訓練分布(サンプリング分布と同義？)は必ずしも好ましいものになるとは限らず、裾が広く、高いエントロピーを持った分布(distribution shiftが起きていたとしても)を用いることが良いパフォーマンスにつながることがわかった。
上記の結果を受けて、adversarial feature matching(AFM,敵対的特徴マッチング)という、エントロピーが高いサンプリング分布を生み出しながら、関数近似誤差を明示的に補償する重み付き分布を提案する。

本研究の貢献は以下のようなものである。

Q-Learningの関数近似、サンプリング、分布シフトに関連する問題を分解して考える'unit testing'フレームワークを導入したこと。
- これにより異なる理由から生じる誤差を制御して観測することが可能になったことで、テーブル形式のQ-Learningで主張されていた、上記に関する多くの問題を実験的に解析を行うことができ、それらの主張が高次元のドメイン(関数近似を必要とするドメイン)でも同様に主張されることがわかった。
高次元のタスクでさえも性能を向上させるような、サンプリング分布の選び方(AFM)を提案した。

本研究全体の目的は、強化学習アルゴリズムをデザインする際の実践的なガイドラインを提供すること・今後の研究で解くべき問題点を明らかにすることである。

2.Preliminaries

Q-Learningアルゴリズムの目的は、最適状態行動価値関数（Q-function）を学習することによって、マルコフ決定過程を解くことである。また、強化学習の目的は、累積割引報酬(リターン)を最大化するような方策(状態を入力にもち、行動を出力する関数)を見つけることである。
(テーブル形式の)Q-Learningアルゴリズムは、ベルマンバックアップオペレーター(ベルマン作用素)による反復計算に基づいたアルゴリズムであり、ベルマン作用素はL-∞ノルムのもとで、縮小写像であり、ある不動点に収束する。この不動点が最適Q-functionである。
状態空間が、テーブル形式で表現することができない場合(連続な実数値空間など)は、関数近似器によってQ-functionを表現することができる。このようなQ-Learning手法をfitted-Q-iteration (FIQ)やapproximate dynamic programming (ADP)と呼び、現在使われているDQNの基礎となる手法である。
FQIは、ベルマン作用素の価値を、Q-functionの関数近似器族に射影して教師あり学習を行う手法であり、以下のような式で表現される。

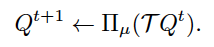
右辺の$ \mathcal{T} $がベルマン作用素を、$\prod_{\mu}$が$\mu$-weithed L2射影を表しています。

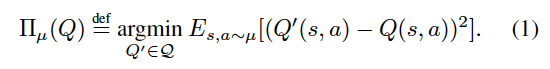
二つ目の式のかっこいいQ($argmin$の$Q'$を要素にもつ集合)は、関数近似器族を表しています。

ベルマン作用素によって生成された$Q^{t+1}$をtarget valueと呼び、ニューラルネットワークが関数近似器として利用されている場合、そのQ-functionをtarget networkと呼ぶ。
本研究では、ベルマンエラーがモンテカルロサンプリングによって推定されたものか、厳密に計算されたものかで場合分けして考えることとする。
$\prod_{\mu}$が$l^2$射影であるのに対し、ベルマン作用素($\mathcal{T}$)はL-∞のもとでの縮小写像である。このミスマッチにより、標準的なQ-Learningの収束性を単純にFQIに適用することができなくなっている。
Q-Learningの関連する手法として、オンラインQ-Learningがあり、これはマルコフ決定過程でサンプリングを行いながらQ-valuesを更新する手法である。
オンラインQ-Learningは、FQIやQ-iterationに対して確率的最適化を適用しているようなものであり、理論的に近い性質を持つことが知られている。

2.Preliminaries 自分用メモ・イメージ

テーブル形式のQ-iteration、すなわち状態行動対$(s,a)$ひとつひとつに対して値を保持しておくことができるような場合は、ベルマン作用素はL-∞での縮小写像であり、収束性が保証されます。(縮小写像なので、各イテレーションの縮小度合いも保証される。)
それに対して、関数近似器を用いているFQIでは、予測のターゲットである値($Q^{t+1}$)を、直交射影作用素によって、関数近似器族の空間に射影しています。(直交射影作用素を施す前の値は、関数近似器族で表現できるとは限らないため、損失関数として利用するために、射影しています。)
つまり、FQIでは、実際の(理想的な)損失関数ではなく、考えている関数近似器族で表現し得る、代理的な損失関数を考えていると言えます。
上記の射影操作によって、関数近似器を用いて学習することができるようになった一方で、元のベルマン作用素の収束性の保証を失ってしまっています。(局所解でも十分な場合は問題ない or 理論的には収束性が満たされなくても、実際はある程度の保証がありそうな(とりあえずやってみたらうまくいった)ために、現状色々な分野で利用されているのかなと思ったりします。)

3.Experimental Setup

本研究の実験では、'unit testing'を中心に据えて設定を行った。

Q-Learningアルゴリズムを連続的な設定として考えた。つまり、動的計画法の厳密な近似から始め、モダンなdeep Q-Learningのアルゴリズム・手法に似るまで、徐々にoracle componentsに置換していくものとした。
olacle solutionsを計算することができる一連のテーブル環境を導入した。
ドメインをまたいで一貫した評価を行うために、リターンとQ-functionに関する損失を、それぞれのドメインでのエキスパート方策(最適方策?)で得られるリターンで正規化した。

3.1 Algorithms

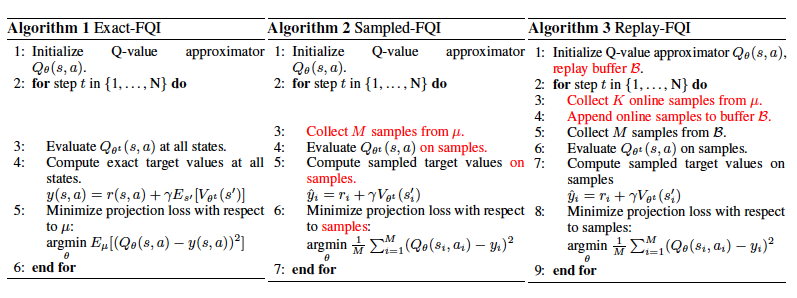
以下の三つのQ-Learningアルゴリズムを4章以降で解析した。(FQIは一般に使われているDQNのアルゴリズムではないが、調整した環境での解析のしやすさから解析対象とした。)

Exact-FQI

サンプリングエラーなしに、全ての状態行動対の更新を計算する。この手法は、ベルマン方程式を計算するために、状態遷移確率・報酬関数(環境)が既知であると仮定している。
本実験では、Exact-FQIを用いて以下の項目を調査した。
- 収束性
- 分布シフト
- サンプリングエラーのない条件での関数近似

Sampled-FQI

Sampled-FQIはExact-FQIの特殊なケースの一つであり、分布$\mu$から得られたサンプルを用いて、ベルマンエラーをモンテカルロ推定したものである。
本実験では、Sampled-FQIを用いて、過学習の影響について調査した。
Sampled-FQIは以下のような、誤差の全ての原因が組み込まれた手法である。
- 関数近似誤差
- サンプリング・分布シフト

Replay-FQI

Replay-FQIはreplay bufferを用いた、Sampled-FQIの特殊なケースと言える。replay bufferは過去の状態遷移のサンプル($s,a,r,s^{'}$)を保存し、ベルマンエラーを計算するのに利用される。
Replay-FQIは、分布$\mu$が変化することを許容するオンライン更新ではないという点においてだけ、DQNと異なるアルゴリズムである。
巨大なreplay bufferを用いることによって、Replay-FQIとDQNの分布の変化の差は微小になるという仮定で考えることとする。

Choice of weighting distribution

上記に加え、本研究ではベルマンエラーのための重み付き分布$\mu$の選択の仕方も調査した。ベルマンエラーをサンプリング(算出)する際、これらは分布からの直接的なサンプリングかimportance samplingによって実装することができる。
- Unif(s,a)：状態行動空間上での一様な重み分布であり、FQIのような動的計画法のアルゴリズムで一般的に利用される分布。
- Random(s,a)：一様ランダム分布で行動を選択した際の状態行動対の分布。
- Prioritized(s,a)：ベルマンエラーの大きさに比例した分布。prioritized replayの、importance samplingを行わない手法と言える。
- Replay(s,a) and Replay10(s,a)：学習中に生成された、全ての方策(or 直近10個の方策)に対して平均をとった状態行動対の分布。これは、それぞれの方策によって生成された無限のサンプルを含むreplay bufferから、一様にサンプリングすることのシミュレーションと言える。

3.2 Domains

本実験では、oracle valuesを計算することができるテーブル環境を8個利用した(詳細はAppendixを参照)。これによって、学習によって得られたQ-functionと真の値であるoracleと比較することで、様々なエラーの原因を解析することができる。

3.3 Function Approximators

本研究ではユニット数が(N,N)で表現される、ReLUを活性化関数とした二層のニューラルネットワークを関数近似器を利用した。
'Tabular'構造は、関数近似を行なっていないケースに相当する。

3.4 High-Dimensional Testing

テーブル環境に加えて、高次元の環境でも同じことが言えるかどうかを調査するために、連続値制御のタスクでも実験を行なった。
連続値のドメインではQ-valueの最大値を計算することが難しく、このような時に取られる一般的な対策である、$max_a Q(s,a)$を近似するためのニューラルネットワークを、二つ目の'actor'として導入する。

3.Experimental Setup 自分用メモ・イメージ

絶対的な正しい値(oracle hogehoge の表現の部分。oracleは「神託の」、つまり天下り的に与えられるground truth。)がわかる環境で、あえて関数近似を利用したアルゴリズムを用いることで、その手法の難点と、その影響の大きさを定量的に評価する試みをしています。
unit testingというのは、アルゴリズムを少しずつ変えることで、部分的にテストしていくことを指しているのだと理解しています。個人的にはbias/variance分解の実験的・経験的な評価に近いものかなと思います。

4 Function Approximation and Convergence

最初に調査する項目は、関数近似と収束性の関係である。

4.1 Technical Background

2章で見たように、関数近似をQ-Learningに導入すると、収束性はうしなわれた。この関数近似と収束性の関係は長い間研究されてきたトピックである。
既往研究から以下のような事実が得られている。
- Q-Learningでは線形の関数近似器でも発散することがある
- on-policy型のTD-Learningにおいて線形の関数近似器を用いると収束する
- GTD,ETDと呼ばれる手法は、この結果をoff-policy型のアルゴリズムとして拡張した
- 調整された環境下で、SBEED,Greedy-DQなどの収束する手法も提案されている
- いくつかの研究で、必ずしも発散しないことがわかっている
  - 与えられた分布$\mu$が十分にサポートしており(サンプルの量・バラツキが十分ということ？)、p-ノルムで射影が非拡大(縮小写像より弱い制約)ならば、unboundedな発散は生じないことが理論的に示された
  - Atari gamesにおいて、DQNの派生形で発散は滅多に起きない

4.2 関数近似はどのように収束性と部分最適性に影響を及ぼすのか

(How does function approximation affect convergence properties and suboptimality of solutions?)

ここでは関数近似とパフォーマンスの関係性を調べるために、関数近似を導入したことによるlearning procedure のバイアスを測定する。
そのために、サンプリングエラーが無いように一様分布から学習するExact-FQIを使って、学習済み方策によって得られるリターン、そして、$Q^*$とExact-FQIの解($lim_{t \to \infty}(\prod_{\mu}\mathcal{T})^t Q^0$)、もしくは$Q^{*}$と最適解の射影($\prod_{\mu}Q^{*}$)との$l^{\infty}$を測定する。
最適解の射影($\prod_{\mu}Q^{*}$)は、FQIでのbootstrappingを行わないで得られた解と言え、関数近似族内での最適解である。したがって、生じるバイアスを関数近似によるものに調整している本実験の環境下において、FQI誤差と射影誤差の差分は、bootstrappingによって生じたものだと考えることができる。この差分をinherent Bellman error(内在的ベルマン誤差？)と呼ぶ。
内在的ベルマン誤差はQ-Learningアルゴリズムのデザインによって改善することができる。

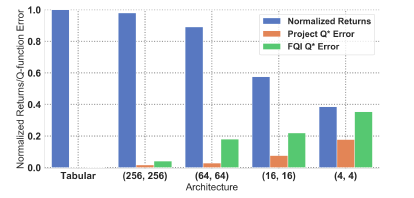
実験結果の図です。Normalized returns/Q-functionはドメイン・seedsに渡って平均を取った値です。
関数近似器が小さいほど、FQI誤差($FQI \, Q^{*} Error$)と射影誤差($Project \, Q^{*} Error$,関数近似族内での最適解)のギャップが大きくなっていることが読み取れます。

一つ目に注目する点として、小さい関数近似器ではリターンの値が小さく、局所最適に陥っている傾向がある。
さらに、小さい関数近似器ではlearning processのバイアスも大きくなっている、つまりExact-FQIと最適解の射影のギャップ(内在的ベルマン誤差？)も大きいことがわかる。
このギャップは、ターゲットがbootstrappedされている場合、全てのQ-functionを単なる最終的な解ではなく、最適解に向かわせることができるような表現力を持たないといけない、ということに由来しているのであろう。

あまり自信がないので本文を載せておきます。：This gap may be due to the fact when the target is bootstrapped, we must be able to represent all Q-function along the path to the solution, not just the final result

この結果は、表現力の大きい関数近似器を用いることは、その表現力の大きさに加えて、bootstrappingを用いた学習がしやすく、収束性の問題にも悩まされにくいという、重要な利点を持つと暗示している。
また、本実験では$Q^{*}$より10倍以上Q-valueが大きくなるような発散は、全体のうち0.9%しか発生していないことを追記しておく。
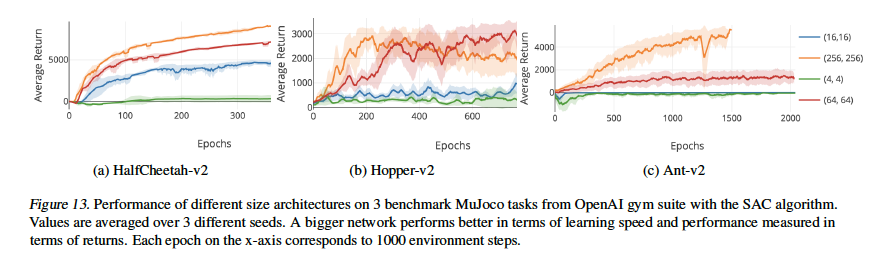
さらに高次元の問題において、SACという学習アルゴリズムのQ-Networkに対しても同様の実験を行い、上記と同様に、大きい関数近似器ほど良いパフォーマンスを発揮し、発散も滅多におきないことが確認された。

unbounded divergenceがほとんど起きていないことに関して、既知の反例と関連づけてAppendix Bで直感的な理解を得るためのdiscussionを行った。

5.Sampling Error and Overfitting

ベルマン誤差の最小化における二つ目の要員として、Q-Learningにおけるサンプリングエラー(or generalization error)を調査した。

5.1 Technical Background

動的計画法ではベルマン作用素が完全に計算できることが想定されているが、強化学習では環境(状態遷移確率や報酬関数)が未知である事が多く、経験的ベルマン誤差しか計算する事ができない。
PACフレームワークにおいて、高い確率で経験誤差と期待誤差のbounded errorを定量的に評価する事ができ、しかもその値はサンプルサイズに比例して減少する事が明らかになっている。

※PAC(probably approximately correct,確率的に近似が正しい)とは、サンプル複雑度が確率的に多項式で抑える事ができるようなアルゴリズムのことです。
また、サンプル複雑度とは選択したアルゴリズムがε最適でない方策(最適方策を用いた時との目的関数の差がεより大きい方策)を採用した回数のことです。

本実験ではサンプリングエラーに関して以下の二点について示す。
- テーブル環境でも高次元環境でも、Q-Learningは過学習しやすく、パフォーマンスに影響を与えること
- replay bufferは過学習に対して有効な手段であり、他にも実用的なテクニックをいくつか存在すること

5.2 Quantifying Overfitting

はじめに、サンプル数を変えることで、学習中に生じる過学習を定量化することを考える。validation errorを異なる実験環境で比較するために、正規化された訓練で得られたN個のQ-functionを取り出して、これらに固定して考える。
その後、再び学習に戻り、射影誤差$\prod_{\mu} (Q^t)$の最小化を各イテレーションで行う。この際、利用するデータはon-policyのデータかreplay bufferからのサンプリングで取得する。
on-policy分布の下で、各イテレーションで厳密なvalidation error(期待ベルマン誤差)を測定し、その結果を下に示す。

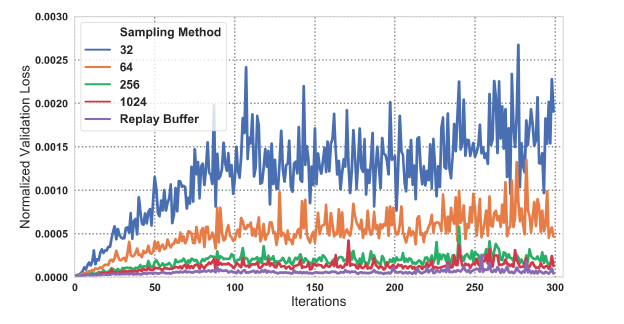
分布シフトがあるにも関わらず、replay bufferからのサンプリングがもっとも小さいpolicy validation lossを得ていることがわかります。

サンプル数が多くなるほど、validation loss、すなわち過学習の度合いが小さくなる傾向が読み取れる。さらに面白いことに、off-policyデータからのサンプリングによる分布のミスマッチがあるのにも関わらず、replay bufferからのデータを用いると最もvalidation lossが小さくなっている。(6章でreplay bufferについて再度言及する)
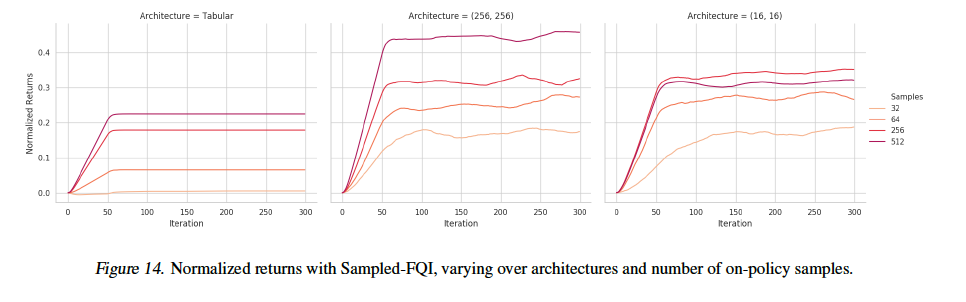
続いて、サンプル数とリターンの値の関係性を下図に示す。

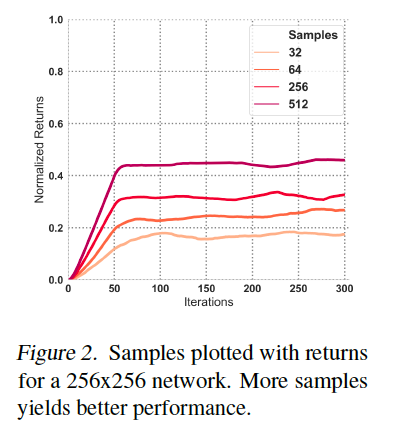
関数近似器のサイズを固定し、サンプルサイズを変更した際のリターンの推移です。

こちらは異なる関数近似器を用いた場合の比較になります。

上記の結果より、サンプル数が多いほど学習速度は上がり、また得られる解も向上する傾向にあることがわかり、過学習はQ-Learningのパフォーマンスに影響を与えるという私たちの仮説が示されたと言える。

5.3 What methods can be used to compensate for overfitting?

一般的に過学習を避けるにはニューラルネットワークの表現力を制限する正則化が行われるが、これまでに見たように、表現力を下げることは得られる解の品質が下がる可能性がある。
そこで、ニューラルネットワークの表現力を下げずに過学習を避ける手法として、early stopping手法について調査する。
はじめに、射影ステップでのサンプル数あたりのnumber of gradient stepsの数がパフォーマンスに大きな影響を与えることが観察された。ステップ数が小さすぎると学習は遅くなり、ステップ数が大きすぎると学習は早いが過学習に陥る。
これを示すために、複数のハイパーパラメータによる学習を行なった。

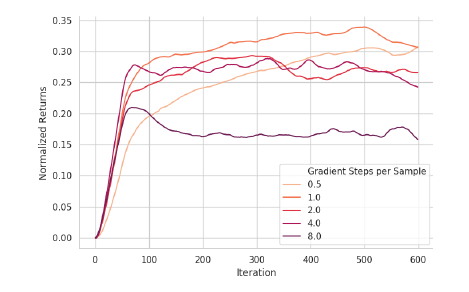
上図はReplay-FQIにおける実験結果です。ステップ数が中間くらいで良い性能が得られており、大きすぎるステップ数では性能が損なわれているのが読み取れます。

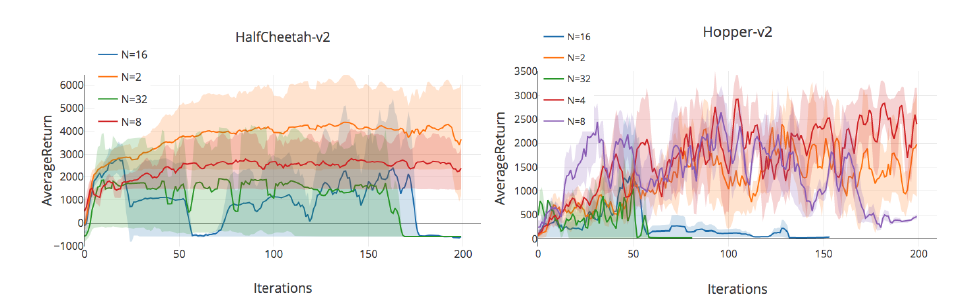
こちらはTD3というアクター・クリティック方式のアルゴリズムでの結果です。replay bufferの大きさが16の時の実験結果であり、Nがステップ数になります。
こちらもステップ数が大きい時は過学習が起きてパフォーマンスが下がっていることが分かります。

過学習を避けるためのearly stoppingの指標にどんなものが良いかを理解するために、oracle early stoppingという手法を提案する。
この手法自体は、実際に過学習を回避するために使われていないが、これらの実験が将来の手法の元となり、最適なstoppingを得るためのupper boundを提供するガイダンスになると考えている。以下では、ステップ数を決定するための二つのoracle early stopping指標を調査した。
- 期待ベルマン誤差を最小にするパラメータ
- greedy方策の期待リターンを最大にするパラメータ
実験では、二つの手法をReplay-FQIの射影ステップで、勾配降下法を用いて最適化を行い、上記の評価指標に則ってQ-functionを選択するというような実装にした。以下に結果を示す。

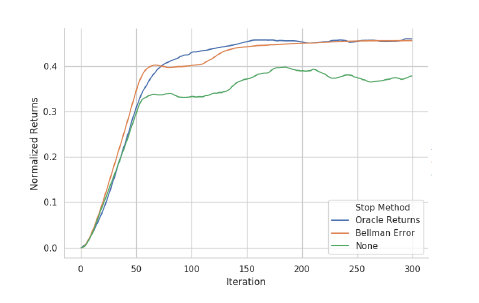
適切なearly stoppingを採用することで、リターンが少し増大していることが分かります。

この実験からいくつかの、実践に活かせる結論が得られたと考えている。
- 過学習は実際に発生するものであり、gradient stepsは多すぎると過学習し、少なすぎると学習が遅くなる。
- replay buffer と early stopping は過学習を抑制する効果がある。
- 過学習は問題ではあるが、それでも表現力の大きい関数近似器が望ましい。なぜなら、小さい関数近似器を用いることによる関数近似誤差の方が大きな問題になるからである。

6. Non-Statinarity

この章では、Q-Learningでの非定常性について議論する。

6.1 Technical Background

Q-Learningの挙動の不安定性は、目的関数の非定常性を原因とすることがしばしばであり、非定常性は主に以下の二つの場所で発生する。
- ターゲット値 $\mathcal{T}Q$の変化
- 重み付き分布$\mu$の変化(分布シフト)、すなわち、異なる方策から得られたサンプルによる学習の問題。
ここで注意する点として、非定常な目的関数それ自体は、非定常性を導くものではないということである。

例：方策勾配法による最適化($\theta^{t+1}$は変化する目的関数。)

$$\theta^{t+1} = \theta^t - \alpha \nabla_{\theta}f(\theta^t) $$

しかし、Q-Learningアルゴリズムが更新による最適化を行うこと、非定常な目的関数が解析を難しくしているのは事実である。GTDなどのアルゴリズムは、勾配降下法のような標準的な最適化を行うために、定常な目的関数を導入している。
したがって、ここで調査する疑問としては、これらの非定常性が、学習プロセスに対して有害なものであるかどうか、ということである。

6.2 Does a moving target cause instability in the absence of a moving distribution?

moving targetの問題を調査するために、はじめにmoving targetの効果を切り離し、どれくらいのレートがパフォーマンスに影響を与えるかを調べる。
target changeの影響を調べるために、確率的近似のような更新を行う$\alpha$-smoothed ベルマン作用素$\mathcal{T^{\alpha}}$を導入する。この$\alpha$-smoothed ベルマン作用素は$\alpha$が0より大きく1以下ならば、縮小写像であり、$Q^{*}$に収束することが理論的に示されている。

$$\mathcal{T^{\alpha}}Q = \alpha \mathcal{T}Q + (1 - \alpha)Q$$

($\alpha$-smoothed ベルマン作用素の縮小性について)

標準的なQ-iterationは$\alpha = 1$のハードな更新であると言える。
上記の定理から分かるように、縮小度合いは小さくなっているため、Q-iterationよりも収束に時間がかかる。しかし、重い関数近似誤差において、より安定したものになるであろう。

原文抜粋：we expect slower convergence, but perhaps it is more stable under heavy function approximation error.

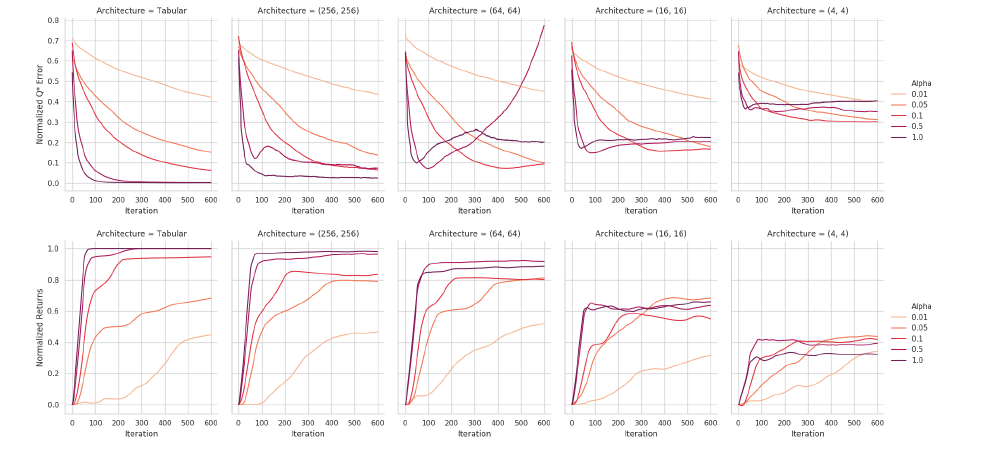
この修正した更新をExact-FQI、一様な重み分布Unif(s,a)に対して適用して実験を行なった。以下に結果の図を示す。

異なる$\alpha$とニューラルネットワークにおける、$Q^{*}$に対する$l^{\infty}$ノルム誤差と、正規化されたリターンがプロットされている。ニューラルネットワークが大きいときは、$\alpha$が大きい時は高速に収束し、問題のないリターン値を得ている。
しかし、関数近似器であるニューラルネットワークが小さい時は、$\alpha$が小さい時の方が大きなリターンを得ている。
したがって、表現力の高い関数近似器を利用している場合でも、重い関数近似誤差の元では、moving targetの変化量を小さくすることは良い影響があると考えられる。

6.3 Does distribution shift impact performance?

分布シフトを調査するために、イテレーション間の分布シフトを、総合的な距離$D_{TV}(\mu^{t+1} || \mu^t )$ を次のように計算することとする。

$$ D_{TV}(\mu^{t+1}|| \mu^t ) = E_{\mu^{t+1}}[(Q^t - \mathcal{T}Q^t)^2] - E_{\mu^{t}}[(Q^t - \mathcal{T}Q^t)^2]$$

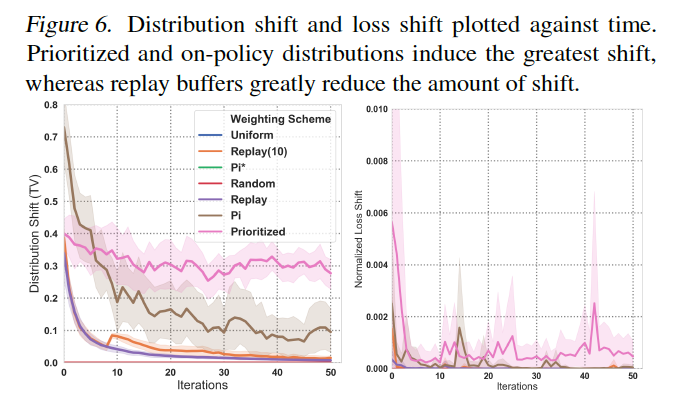
損失シフトは、新しい分布のもとでベルマン損失が評価される時、もし分布がこれまでに未観測の、もしくは良くサポートされていないものにシフトする場合、そのような状態(情報が少ない状態)のQ-valueは真の値から大きく離れたものになり、損失シフトも大きくなると予測される。
本実験では関数近似器のサイズを固定したExact-FQIを用いて実験を行い、得られた分布シフトと損失シフトを以下の図に示す。

Prioritized,on-policyによる分布は大きなシフトを誘導している一方で、replay bufferはシフトの量を大きく減少させていることがわかる。
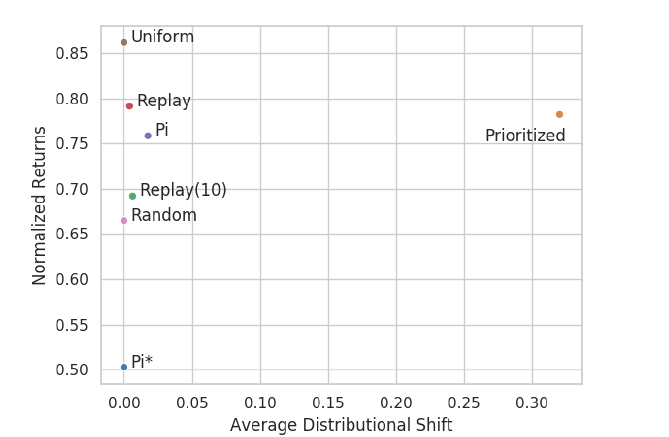
しかし、この指標は実際のアルゴリズムのパフォーマンスとの相関がかなり小さいことが以下の図から読み取れる。

本実験の結果は、分布とtarget valueの非定常性は、大きな不安定性の問題を引き起こしていないことを示唆している。事実、サンプリングエラーや関数近似誤差の方がパフォーマンスに大きく影響している。
これらの発見の元、本研究では、パフォーマンスが向上するようなサンプリング分布をデザインすることができるか、ということについて調査を加える。これを考える際には、分布シフトやエントロピーの大きさは無視し、最終的なパフォーマンスを高めることだけを考え、またこれが実応用可能なものかを考察する。

7.Sampling Distributions

6章の結果よりサンプリング分布のデザインは、アルゴリズムのパフォーマンスを決定する要因の一つであることがわかったが、実際にどのようなサンプリング分布を用いるべきかは明確ではない。
そこで本章ではこの問題について調査を進める。

7.1 Technical Background

off-policyデータは、Q-Learningにおいて不安定性をもたらす可能性がある、致命的なものと考えられており、off-policynessを改善するための手法として、importance samplingがよく利用されている。
一方で、on-policyもしくは固定された行動方策によって得られたデータ分布については、収束性の理論的な解析がなされてきている。
しかし、私たちの知る限りでは、重み分布の違いの度合いが、収束性と最終的に得られる解に対してどのくらい影響を及ぼすかの研究はあまりされてきていない。
上記のような状況にも関わらず、いくつかの研究は重み分布の選択の仕方について仮説を与えてくれる。
- more uniformな重み分布は、最悪ケースの誤差限界を与える(Munos,2005)
- 状態分布が固定されているならば、行動分布はベルマン残差に対する最適方策にしたがって重み付けするべき(Geist et al.,2017)
- 深層強化学習においては以下の手法が有効であることが経験的に知られている。
  - prioritized replay(Schaul et al.,2015)
  - mixing replay buffer with on-policy data(Hausknecht&Stone,2016;Zhang&Sutton,2017)
本実験では、どの重み分布を用いることが最も効率的なのかを、経験的に解析することで明らかにする。

7.2 What Are the Best Weighting Distributions in Absence of Sampling Error?

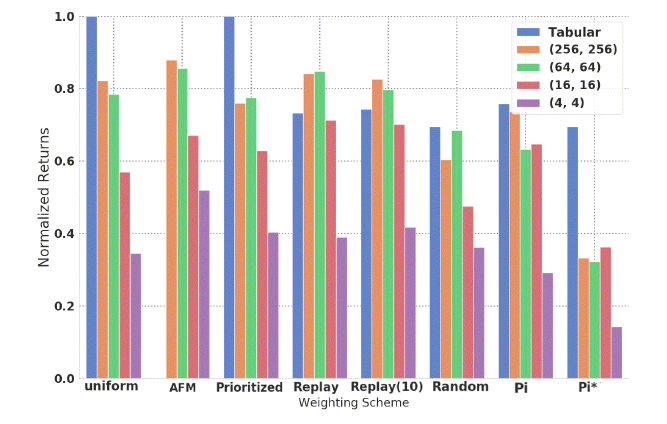
まず、重み分布の影響を、サンプリングエラーを分解することで考えるために、Exact-FQIを異なるニューラルネットワーク、重み分布で学習させた。その結果を下に示す。

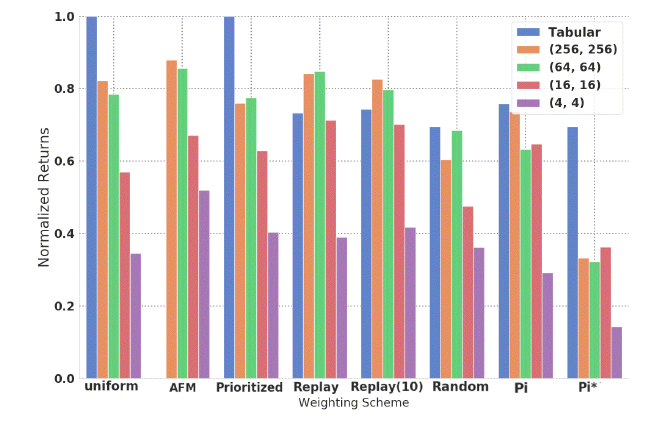
Replay(s,a)は軒並み良いパフォーマンスを達成しているが、AFM(Adversarial Feature Matching)はReplay(s,a)に匹敵し、特に小さい関数近似器で良いパフォーマンスを達成している。
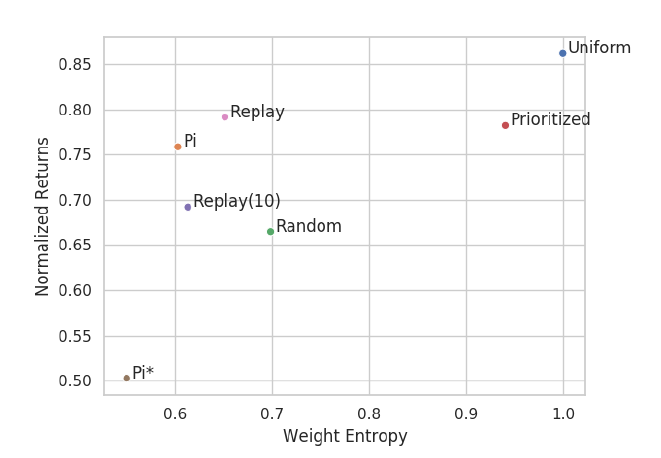
上記の結果より、私たちは'uniformity hypothesis'を示すものではないかと考える。'uniformity hypothesis'とは、分布がより多くの状態行動をサポートしているほどパフォーマンスがよくなる、という仮説である。
具体的な解釈としては、replay buffer は複数の方策から得られたサンプルを含んでいるので、一つの方策から得られる状態行動分布よりも、幅が広いものとなるため、良いパフォーマンスが得られる、というようなものである。
この一般的な傾向は、下図のリターンと重みのエントロピーの散布図にも現れている。

この結果は、coverageを最大化するような探索アルゴリズムをサンプル収集の際に適用することを推し進めるものであると言える。
しかし、本実験は特殊な環境であり、サンプリングは行われていないことには注意するべきである。つまり、全ての状態は観測済みであり、分布の問題をサンプリングの問題から切り離しているということである。

→replay bufferや履歴データとして、与えられているデータをどのように学習(パラメータ更新)に用いるか、という問題についての見解であり、どのようにデータを集めるか、またサンプリングエラーに関しては言及していない、ということです。

7.3 Designing a Better Off-Policy Distributions:AFM

前節から得られた、以下の三つの洞察を用いて、深層強化学習に簡単に実装することができる重み分布を提案する。
- 関数近似器は、関数近似バイアスを最小化するために状態をよく区別することができるべきである。(表現力は高い方が良い)
- 重み分布は、$l^2$ノルムエラーと$l^{\infty}$ノルムエラーの差を最小化するために、ベルマン誤差が大きい場所を強調するべきである。(関数近似による誤差が大きいところを重点的に学習す流方が良い)
- よりuniformな分布の方が高いパフォーマンスを達成する
本研究では上記の問題をmin-max gameとして定式化したモデルを考える。
- $p_{\phi}(s,a)$:ベルマン誤差を最大化しようとする、重み分布の敵対的パラメータ
- $Q_{\theta}(s,a)$:ベルマン誤差を最小化しようとする、Q-function
注意点として、制限のない環境下では、この定式化は$l^{\infty}$ノルム誤差を、双対ノルム表現で最小化することと等価であることが挙げられる。
しかし、$l^{\infty}$ノルムを確率的近似によって最小化するような現実的な問題は、ニューラルネットワークにとって難しい問題であることが知られている。そのため、敵対的な表現に対して制約を導入することは重要な操作となる。
この制約により、重み分布は広がりを持つことを目指しながらも、特定の状態行動対に対してはよくサンプリングするような分布になることが期待される。
本研究では特徴マッチング制約を導入する。特徴マッチング制約とは、重み分布が$p_{\phi}(s,a)$の場合の期待特徴ベクトル$E[\Phi(s)]$と、replay bufferから一様にサンプリングする場合の期待特徴ベクトルが、「粗く」マッチングするように制限することである。
ニューラルネットワークの出力であるQ-functionを、$Q_{\theta}(s,a) = w_a^T \Phi(s)$、(連続値の場合は$Q_{\theta}(s,a) = w_a^T \Phi(s,a)$)と表現することができるとき、期待特徴ベクトル$\Phi(s),\Phi(s,a)$は、ニューラルネットワークの最終レイヤの出力を表している。
これは直感的には、敵対的サンプラー(重み分布)は、Q-functionに似ているような状態(or 状態行動対)に確率を振り分けていくと考えることができる。これはより区別できるような状態の特徴を学習することで、state-aliasingを減少させるような操作とも言える。

※aliasingというのは、本質的に異なる連続的な信号が標本化(連続時間を1秒とかで区切るような離散化操作)によって区別できなくなってしまうこと、だそうです。
つまり、状態の特徴ベクトルが近いものをよくサンプリングすることで、似ている状態を繰り返し学習することになり、それらを区別することができるようになる、ということだと思います。

本研究では重み分布のパラメータは$\phi(s,a) = \nabla_w Q_{w,\theta}(s,a)$として定式化した。
この手法は、ニューラルネットワークの最終レイヤの出力だけのマッチングではなく、全てのパラメータにおけるマッチングのような自然な拡張が考えられるが、本研究では取り扱わない。
目的関数は以下のように定式化される。

目的関数
$$ min_{\theta,w}max_{\phi} E_{p_{\phi}}(s,a)[(Q_{w,\theta}(s,a) - y(s,a))^2]$$
制約条件
$$ s.t. \, || E_{p_{\phi}(s,a)}[\Phi(s)] - \frac{\sum_i\Phi(s_i)}{N} || \leq \varepsilon $$

$\Phi(s)$は$\theta$の関数であるが、最大化を計算する際には、$\theta$は定数として扱う。AFMの実装の詳細についてはAppendix Dで記述する。(今回の記事では扱いません。また別の記事として取り上げるかも...?)
$\frac{\sum_i\Phi(s_i)}{N}$はあるサンプリング分布(一様分布やreplay buffer分布)の元での真の期待値の推定になるので、replay bufferを利用しているときは $\frac{\sum_i\Phi(s_i)}{N} \approx E_{p_{rb}}[\Phi]$ の近似が成立する。
PER(prioritized replay)もAFMも大きなベルマン誤差を与えるサンプルに重みを追加する仕組みであるが、PERは明示的に分布シフトが小さくなるような定式化である点で異なる。しかし、7章でみたように分布シフトは実用上は大きな問題にはならないため、AFMでは敵対的な最適化によってより良いcoverageが得られるような定式化にした。

実験結果を再掲します。

Exact-FQIをテーブル環境で用いた場合、AFMはUnif(s,a)やPrioritized(s,a)よりも良い性能を発揮したことから、適応的な優先度付けはPrioritizedよりも良いことが示された。また、AFMの他の利点として、より小さい関数近似器でのパフォーマンスが高いことが重要な特徴である。
同様にReplay-FQIでもAFMとPERを比較したところ、リターンに関しては同様の性能を発揮した。
AFMはbufferから一様に取り出されるサンプルに対して重みを再分配するのに対し、PERはどのサンプルを実際に取り出すかを変更する点で異なる。この点から、AFMの、重みの再分配ではなく実際に取り出すサンプルを変更するように変更した派生系(AFM + Sampling)を考え、同様に実験を行なった。
AFM + Samplingはimportance samplingではなく、AFM最適化によって得られた重みを使ってreplay bufferからサンプルを取り出す。

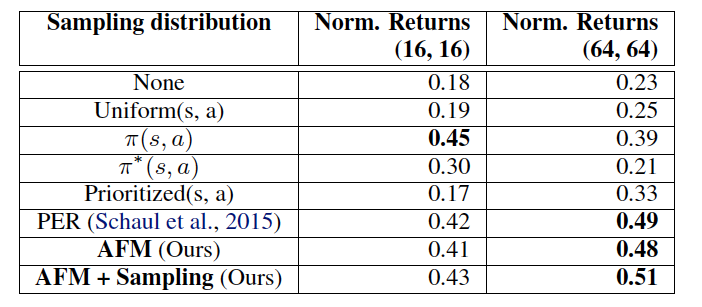
AFM + SamplingはAFMとPERよりも多少改善していることがわかります。

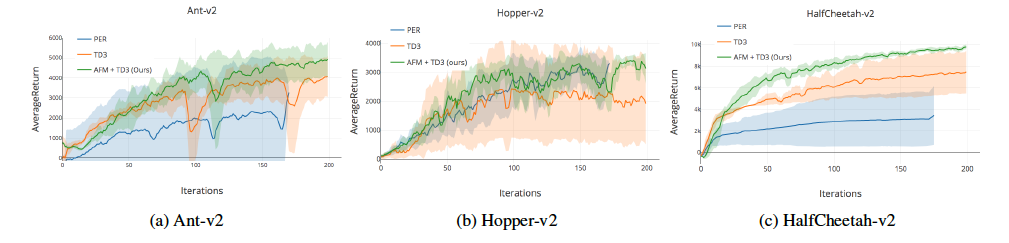
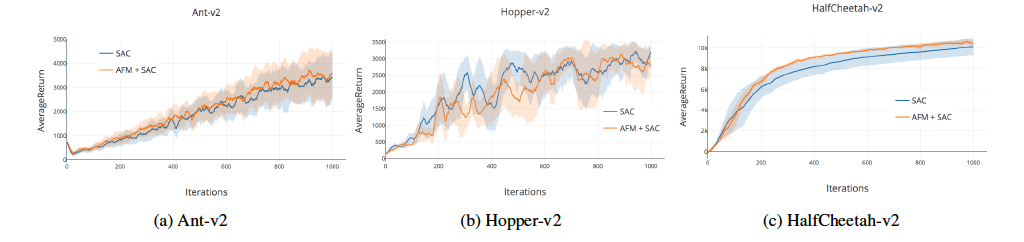
さらにAFMをMuJuCOのような高次元の環境で、TD3アルゴリズムとSACアルゴリズムで実験を行なったところ、TD3アルゴリズムではそれなりの、entropy costrained SACアルゴリズムではわずかな改善が見られた。

TD3アルゴリズム

entropy constrained SACアルゴリズム

驚くべきことに、これらのドメインではPERはうまく働かないという結果が得られた。
以上の結果から、以下のような結論が得られる。
- サンプリング分布の選択はパフォーマンスに大きく影響する
- サンプリング/重み分布選択の際に関数近似器の知識を組み込むこと(\Phi(s)などを通じて)は、有効である

8. Conclusions and Discussion

以上の解析結果から、私たちはDQNアルゴリズムをデザインする上でいくつかの有用な知見を得た。

Potential convergences issues
- 関数近似を行うことは収束性に対して影響を与えるが、大きな関数近似器を用いることで、この問題を以下のような点から緩和することができる。
- bootstrapping errorの影響を緩和する
- 収束が早くなる
- moving targetに対して安定的である

** Sampling error **
- sampling errorはQ-Learningを過学習させる可能性があるが、replay bufferとearly stoppingはこの問題を緩和することができる。
- 私たちは、ベストプラクティスはニューラルネットワークの構造を大きい状態で保つことだと信じているが、サンプルあたりの勾配ステップ数は慎重に選択する必要があることも述べておく。
- oracle ealry stoppingはQ-Learningのパフォーマンス向上に役立つことを示したが、これは将来的に、勾配ステップ数をハイパーパラメータとして与えるのではなく、early stopping techniquesが動的にステップ数を変えるような手法があり得ることを示している。

** The choice of sampling or weighting distribution **
- サンプリング/重み分布の選択は、サンプリングエラーがある場合においても、最終的に得られる解に大きな影響を与えることが示された。
- 驚くべきことに、on-policy分布が最良な選択ではなく、より高い状態エントロピーを持ち、広く様々な状態行動対に重みを割り振るような手法が効率的であることが示された。
- これらの洞察から、高いエントロピーとstate aliasingのバランスをとるAFMという手法を提案し、これによってテーブル環境・高次元環境においてoff-policyのSOTA手法を改善することに成功した。

終わりに
Q-Learningにはover estimationやmulti-step returnsといった他にも多くのトピックが存在している。
私たちは、これらの問題も oracle-based analysisのフレームワークによって調査することができると信じている。

Diagnosing Bottlenecks in DQN Algorithms 論文まとめ