単位根(ADF)検定と分数次差分

株などの時系列データについて一般的にその特微量（始値、高値、終値等）は非定常のデータになります。

ファイナンス機械学習第五章では

通常、教師あり学習のアルゴリズムには定常的な特微量が必要である。その理由はこれまでみた事がない（ラベルづけされていない）観測値を事前にラベルづけされた学習データの集合へとマッピングすることで、新しい観測値のラベルを推論するためである。もし、特微量が定常でなければ新しい観測値をたくさんの既知の学習データへとマッピングする事ができない。

とある。

もし、特微量が定常でなければ新しい観測値をたくさんの既知の学習データへとマッピングする事ができない。

非定常のデータはトレンドを持つので既知の学習データをマッピングしようとすると不整合になるという事であろうか？
疑問点はあるが定常データに変換した方が良さそう。

そのデータが定常か非定常かは単位根(ADF)検定によって判定できる

import pandas as pd
from statsmodels.tsa import stattools
from mlfinlab.features.fracdiff import FractionalDifferentiation

OUTPUT_PATH = '../../data/output/'
df = pd.read_pickle(OUTPUT_PATH + 'df_init_data.pkl')
df_tmp = df[df.index >= '2020-01-01 00:00:00']
df_tmp = df_tmp[df_tmp.index <= '2020-03-31 23:59:49']

df_init_data.pkl は事前にダウンロード済みの日経225miniの分足データ
データ量は制限しないとメモリが足りなくなる＋終わらないので３ヶ月分のデータに制限する

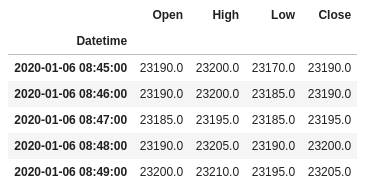
以下のようなデータとなっている

df_tmp[['Open', 'High', 'Low', 'Close']].head()

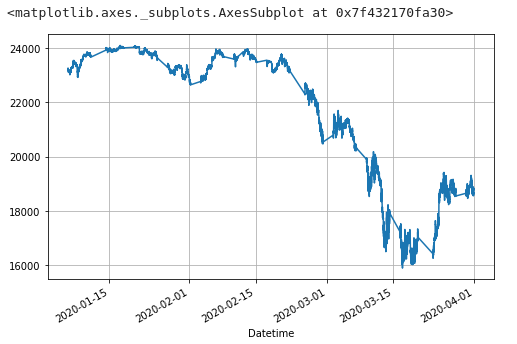
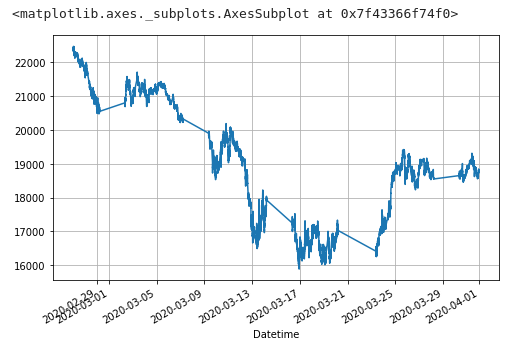
今回は初値についていろいろやってみる

df_tmp['Open'].plot(grid=True, figsize=(8, 5))

単位根(ADF)検定

open_values = df_tmp['Open'].values

ctt = stattools.adfuller(open_values, regression='ctt')
ct = stattools.adfuller(open_values, regression='ct')
c = stattools.adfuller(open_values, regression='c')
nc = stattools.adfuller(open_values, regression='nc')

print('ctt', ctt)
print('ct', ct)
print('c', c)
print('nc', nc)

print('p value', ctt[1], ct[1], c[1], nc[1])

p値は0.01を判定値とした場合、大幅に超えている為、初値は非定常のデータという結果となっている

分数次差分

分数次差分を実行して非定常から定常への変換を試みる

fdiff = FractionalDifferentiation()
df_fdiff = fdiff.frac_diff(df_tmp[['Open']], 0.05)
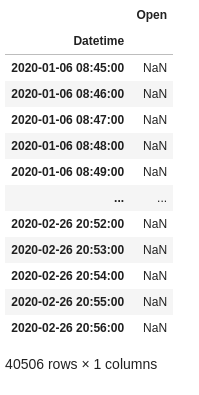
df_fdiff[df_fdiff['Open'].isnull() == True]

結果を取るとなぜか前半の3分の2ぐらいがNaNになっている。

NaN以外で変更前後の比較

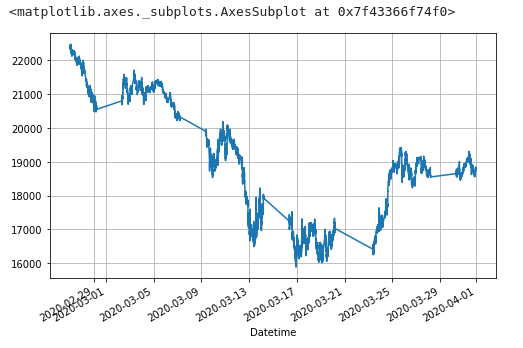
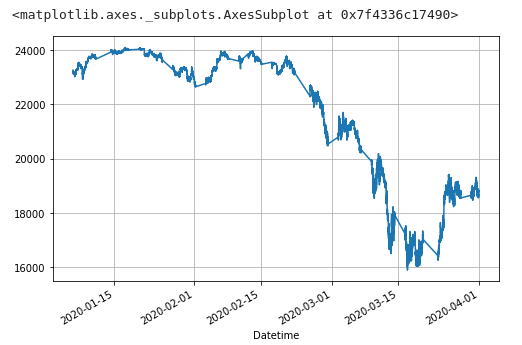
変更前

df_tmp[df_tmp.index >= '2020-02-27 00:00:00']['Open'].plot(grid=True, figsize=(8, 5))

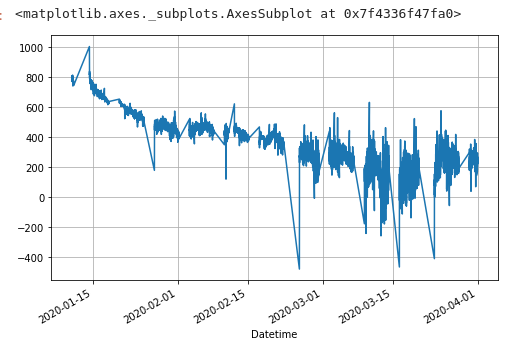
変更後

df_fdiff = df_fdiff.dropna()
df_fdiff['Open'].plot(grid=True, figsize=(8, 5))

目視では違いがよくわからないレベル・・・

最適なD値の判定

有意水準1%として分数次差分変換と単位根(ADF)検定を繰り返す

d_value = 0.05

while True:
    d_value = int((d_value + 0.01) * 1000) / 1000
    print('d_value', d_value)

    fdiff = FractionalDifferentiation()
    df_fdiff = fdiff.frac_diff(df_tmp[['Open']], d_value)
    df_fdiff = df_fdiff.dropna()
    open_values = df_fdiff['Open'].values

    c = stattools.adfuller(open_values, regression='c')
    print(c[1])
    if c[1] <= 0.01:
        print(c[1])
        break

手元の環境ではD値がd_value 0.358を超えると定常データへの変換が確認できた

d_value 0.348
0.011222245001914027
d_value 0.358
0.008607301881316795
0.008607301881316795

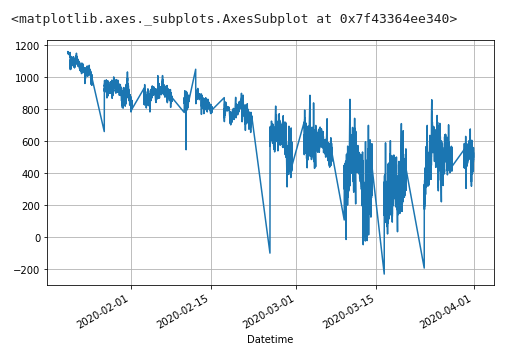
変更前後でプロットしてみる

変更前

変更後

もはや違うデータのように見受けられるw

有意水準5%とした場合の値は以下

fdiff = FractionalDifferentiation()
df_fdiff = fdiff.frac_diff(df_tmp[['Open']], 0.298)
df_fdiff['Open'].plot(grid=True, figsize=(8, 5))

1%とあまり変わらない・・・

この後の10%ぐらいまでを許容範囲とするかは分数次差分の変換をかけた後の特微量でのパフォーマンス次第であろう。

注意点

注意点として単位根(ADF)検定はすごいメモリを食う。
最初5年ぐらいのデータで実施していたが60GB以上、メモリを積んでいるPCで死んだ。

単位根(ADF)検定と分数次差分変換両方ともCPUリソースを食う、プラス時間がかかるため従量課金となるクラウド環境などで行う場合は要注意。