はじめに
この記事は面積についてpythonで理解を深められるかもしれないもの。手っ取り早く3Dの2変数関数の曲面を描きたいだけの人は下のURLを参照。
mplot3dでの3次元空間内への「点」の打ち方については下のURLを参照。
また筆者はプログラミング歴が浅いのでプログラムの効率が悪いかもしれない。ご了承願いたい。
発端
筆者は上記のサイトを読んで曲面の方程式を満たすような点を大量に生成しmplot3dで3次元空間内にプロットすれば三次元のグラフを描けそうだと思ってやってみた。以下のように一様分布でxとyの組を生成しそれに対応するzを陽関数表示で求めた。
for i in range(10000):
X = random.random()#0から1まで一様に値を生成
Y = random.random()
Z = (X**2 - Y**2)/(X**2 + Y**2)**2
x = np.append(x, X)
y = np.append(y, Y)
z = np.append(z, Z)
傾きが大きいとスカスカに
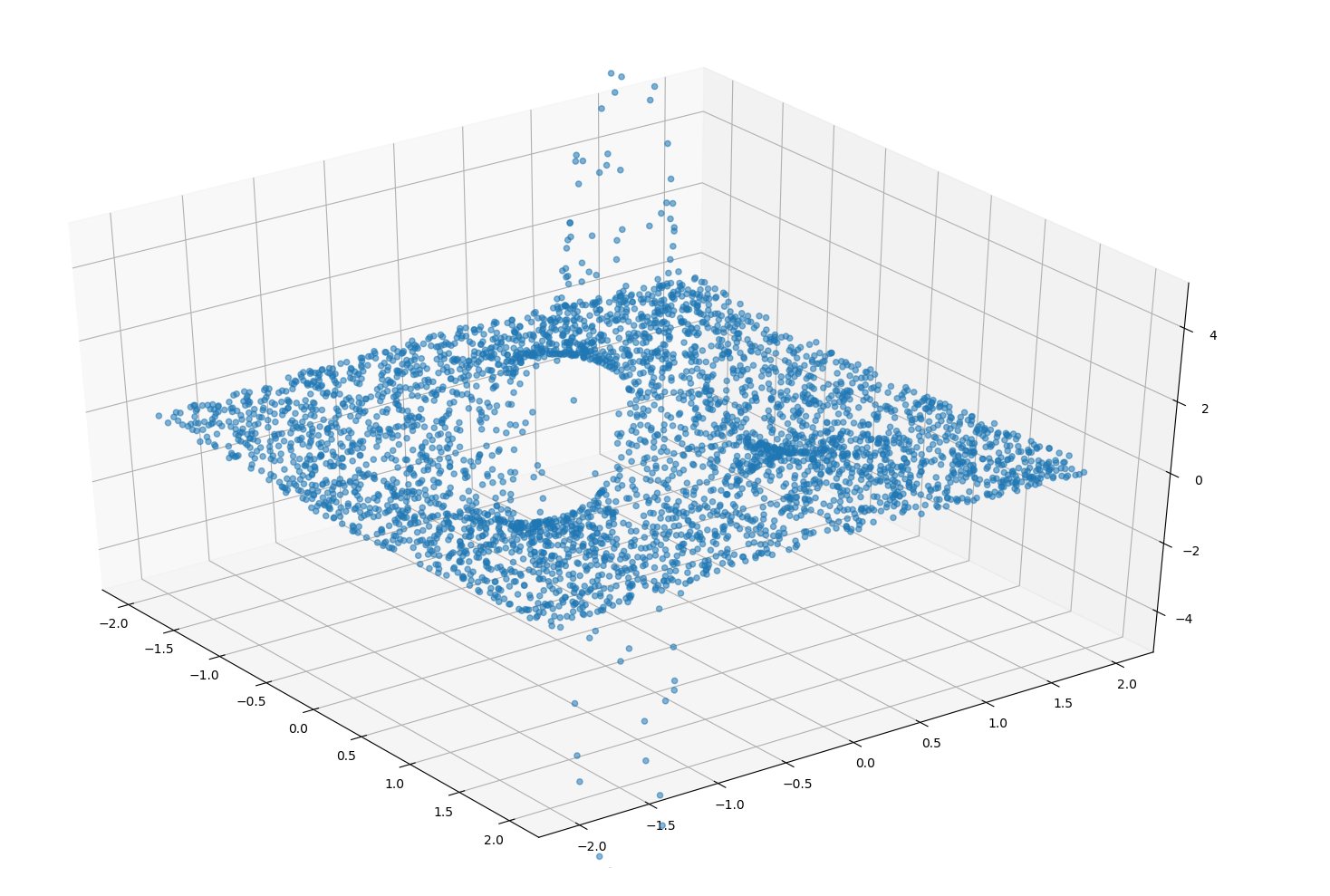
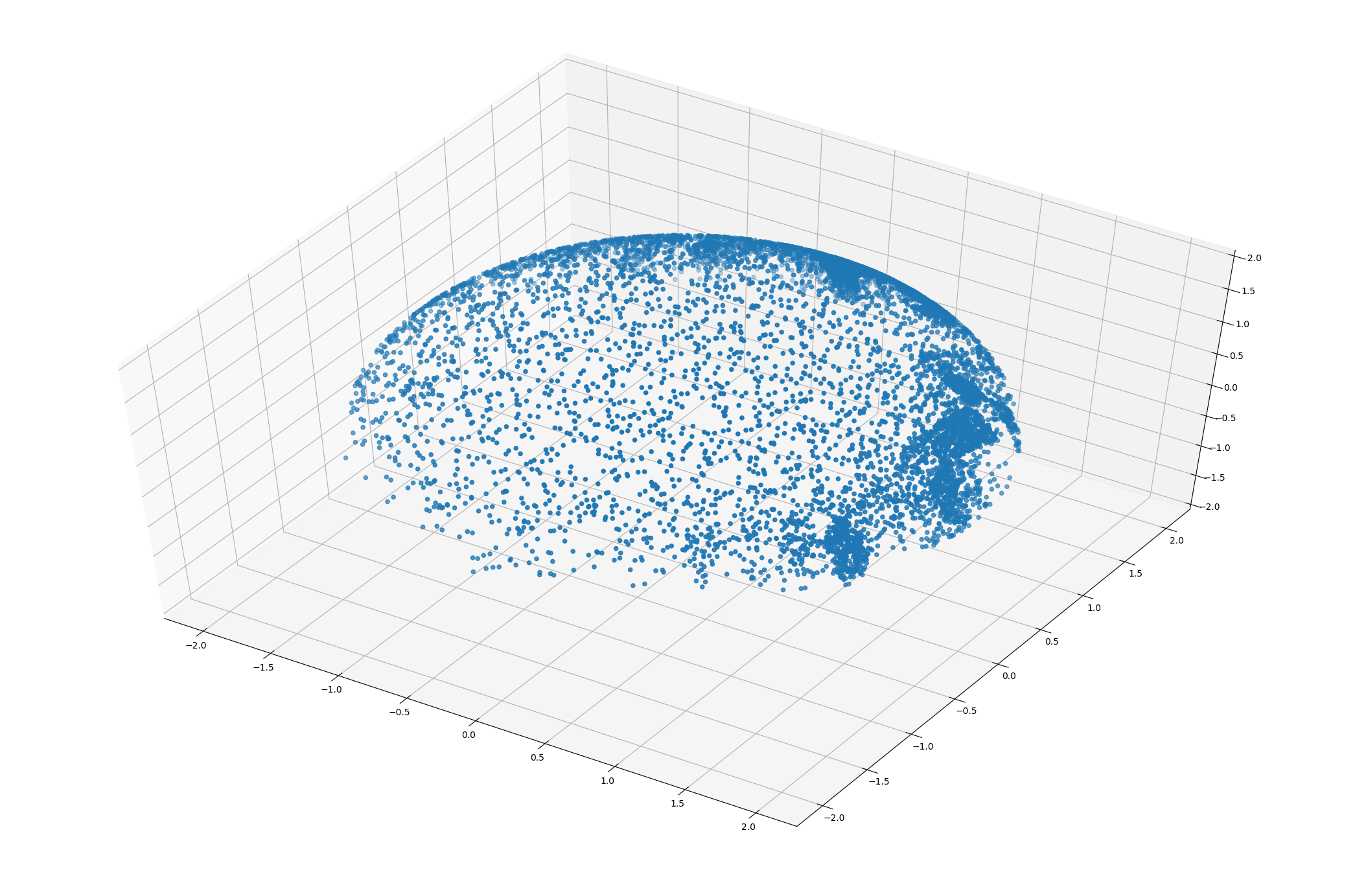
しかしこの方法は問題がある。傾きが大きいと面積あたりのプロットの数が減り、スカスカ(過疎状態)になるのだ。例えば上記コードの半球面では頂点付近に点が密集し周辺に行くに連れて点在するようになる。別な関数では中央ではほとんど垂直になるため下の画像のようになる。
これでは形状が捉えにくい。そこで傾きが大きくても単位面積あたりのプロット数(散布の面密度)が変わらないようにしてみた。以下のような手順のプログラムになる。
1.データを生成するx, yの範囲を細かい小区間に分割する。
2.小区間ごとに曲面を平面で近似し法線ベクトルを求める。
3.z方向と法線ベクトルの方向との余弦cos(θ)(相関係数に等しい)を求める
4.小区間のプロット回数が3で求めた余弦cos(θ)の逆数に比例するようにして少区間ごとに点を生成する。
5.プロットする。
分割が十分細ければ1/cos(θ)は面素dSをx,yの微小変化の積dxdyで割った値に等しい(はず)。
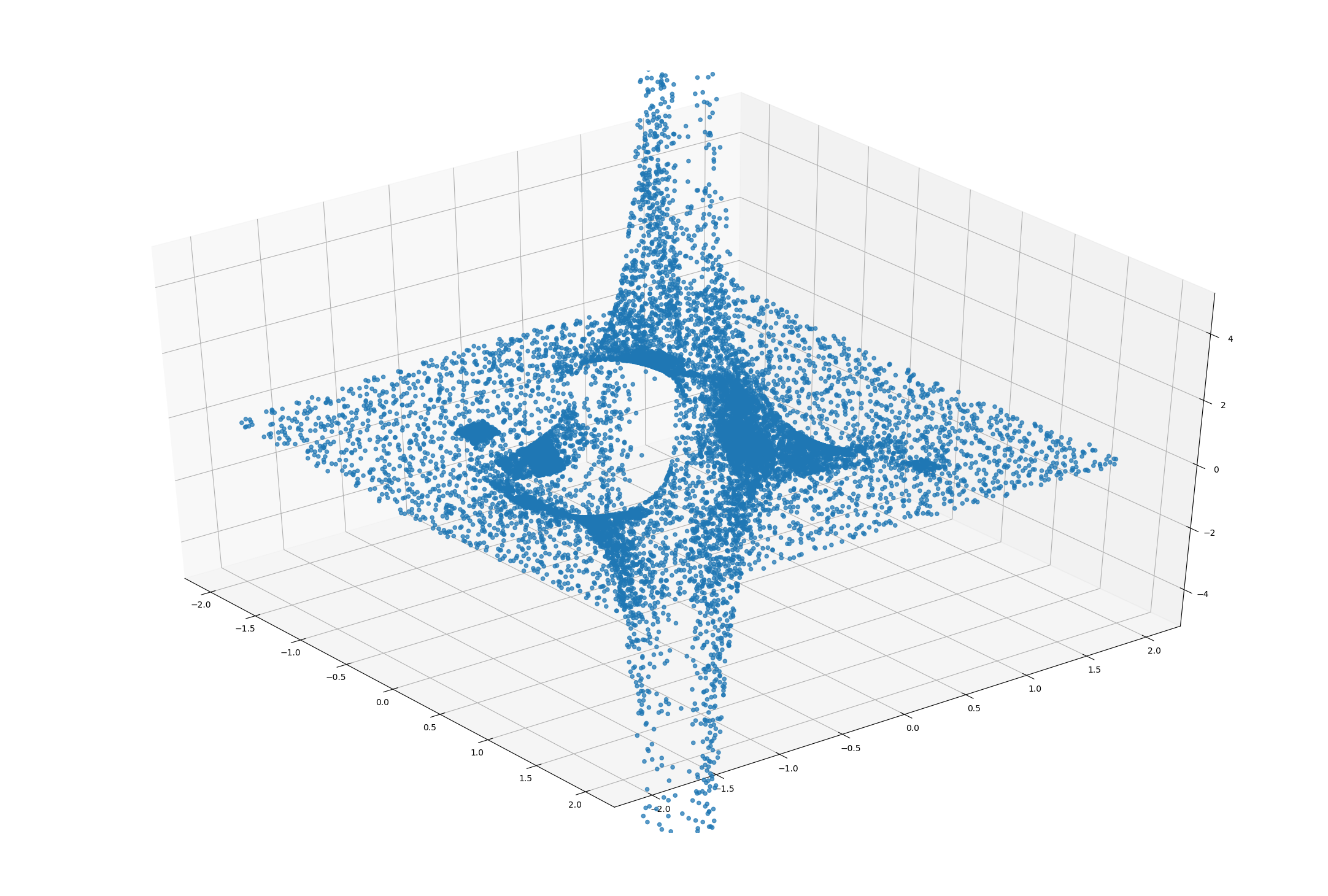
で、実装したら上記のグラフはこうなった↓(範囲や縮尺、角度はほぼ同じ)。
垂直に近くても面密度がほぼ変化していない。
半球の場合
z = (2**2 - (x**2 + y**2))**(1/2)
コード
メソッド定義はなるべく基本的なメソッドのみを使っている。ライブラリを駆使すればもっと短く書けるかも(筆者は詳しくないので)。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
import math
def fun(x, y):
#Define explicit function here.
z = (2**2 - (x**2 + y**2))**(1/2)
return z
# 以下のメソッドだけでも曲面は描けるが傾きが大きいとスカスカに。
# 一様分布はx, y方向に一様であり、曲面に対しては一様でない。
def small_range_random_plot(a, b, c, d, n):
x = np.array([])
y = np.array([])
z = np.array([])
for i in range(n):
X = random.random()*(b-a) + a
Y = random.random()*(c-d) + d
Z = fun(X, Y)
x = np.append(x, X)
y = np.append(y, Y)
z = np.append(z, Z)
return x, y, z
# 小区間で面積が何倍になっているかを調べプロット数を決める
def get_plot_n(a, b, c, d, n, k=100):
Ns = np.zeros(k)
for i in range(k):
x = np.array([])
y = np.array([])
z = np.array([])
for j in range(3):
X = random.random()*(b-a) + a
Y = random.random()*(d-c) + c
Z = fun(X, Y)
x = np.append(x, X)
y = np.append(y, Y)
z = np.append(z, Z)
s = [x[1]-x[0], y[1]-y[0], z[1]-z[0]]
t = [x[2]-x[0], y[2]-y[0], z[2]-z[0]]
cp = np.cross(s, t)
N = n/np.corrcoef([0, 0, 1], cp)[0, 1]#corrcoefは相関係数
if not math.isnan(N):
Ns[i] = N
if math.isnan(np.std(Ns)):
n = 0
else:
n = int(abs(np.std(Ns)))
return n
# 小区間に分割(np.linspaceやnp.meshgridを使ったほうがいいかも)
def split_large_area(a=-1.0, b=1.0, c=-1.0, d=1.0, n=100, m=100):
sps = np.zeros((n, m, 4))
for i in range(n):
for j in range(m):
sps[i][j] = [a+((b-a)/n)*i, a+((b-a)/n)*(i+1), c+((d-c)/m)*j, c+((d-c)/m)*(j+1)]
return sps
def surface_uniform_plot(xl_min=-2.0,xl_max=2.0, yl_min=-2.0, yl_max=2.0, x_split_times=4, y_split_times=4, standard_n=10):
x = np.array([])
y = np.array([])
z = np.array([])
sps = split_large_area(xl_min,xl_max, yl_min, yl_max, x_split_times, y_split_times)
for i in range(len(sps)):
for j in range(len(sps[i])):
rectified_n = get_plot_n(sps[i][j][0], sps[i][j][1], sps[i][j][2], sps[i][j][3], standard_n, 100)
X, Y, Z = small_range_random_plot(sps[i][j][0], sps[i][j][1], sps[i][j][2], sps[i][j][3], rectified_n)
x = np.append(x, X)
y = np.append(y, Y)
z = np.append(z, Z)
return x, y, z
# 縦横それぞれ30分割で座標リストを取得
x, y, z = surface_uniform_plot(-3, 3, -3, 3, 30, 30, standard_n=8)
# 描画
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z)
ax.set_zlim(-2,2)
plt.show()
おわりに
あとで気づいたがこのプロット数から理論上は面積を推定できる。
div_size = 20
standard_n = 8
a = -3.0
b = 3.0
c = -3.0
d = 3.0
x, y, z = surface_uniform_plot(a, b, c, d, div_size, div_size, standard_n)
S_0 = (b-a)*(d-c)
S = (len(x)/(standard_n * div_size**2))*S_0
print("総プロット数" + str(len(x)))
print("推定面積" + str(S))
だが実際には正しい値は出なかった。get_plot_nでのintへのキャストの影響をなくし、特異積分を含まない関数(x^2+y^2など)で試したが面積が実際の半分くらいで出力される。
面積をより正しく出せることはより一様性が高いということだからそのうち原因を突き止めたい。