LoginSignup
3
4
@chicken_data_analyst(ひよっこ アナライズ)

「Rではじめる地理空間データの統計解析入門」を衛星データを使って実践

Last updated at Posted at 2023-04-24

はじめに

「Rではじめる地理空間データの統計解析入門」を買った。（けっこう前に）
空間統計って正直全然触ったことがなくて、興味本位で本を買ったら知らない概念がたくさんあって面白かったので実践してみようと思ったわけ。

しかし、基本的にこの本はベクターデータの解析について書かれている。
まあそりゃあ「A市は、隣接した市町村B,C,Dよりも○○だ。」みたいな解析するにはベクターデータのほうがいいよね。

一方、個人的にGISに関連して興味のある対象って衛星データだったりしたので、「衛星データってラスターデータじゃん。空間統計解析どうするの？」となった。

「いや、ラスターデータ⇒ベクターデータへ変換して空間統計解析をしたらいいのか…」と思ったので、衛星データをラスターデータからベクターデータに変換し、空間統計解析(入門)をすることにした。

え？フリーでもGISソフトあるし、そっちでやったらすぐできるだろって？
…自分でコード書いてできるようになりたいじゃん…。(自己満)

作業の流れとしては下図のような感じ。NDVI(植生指標)を計算して植生の市町村単位の空間統計解析(入門)をする。
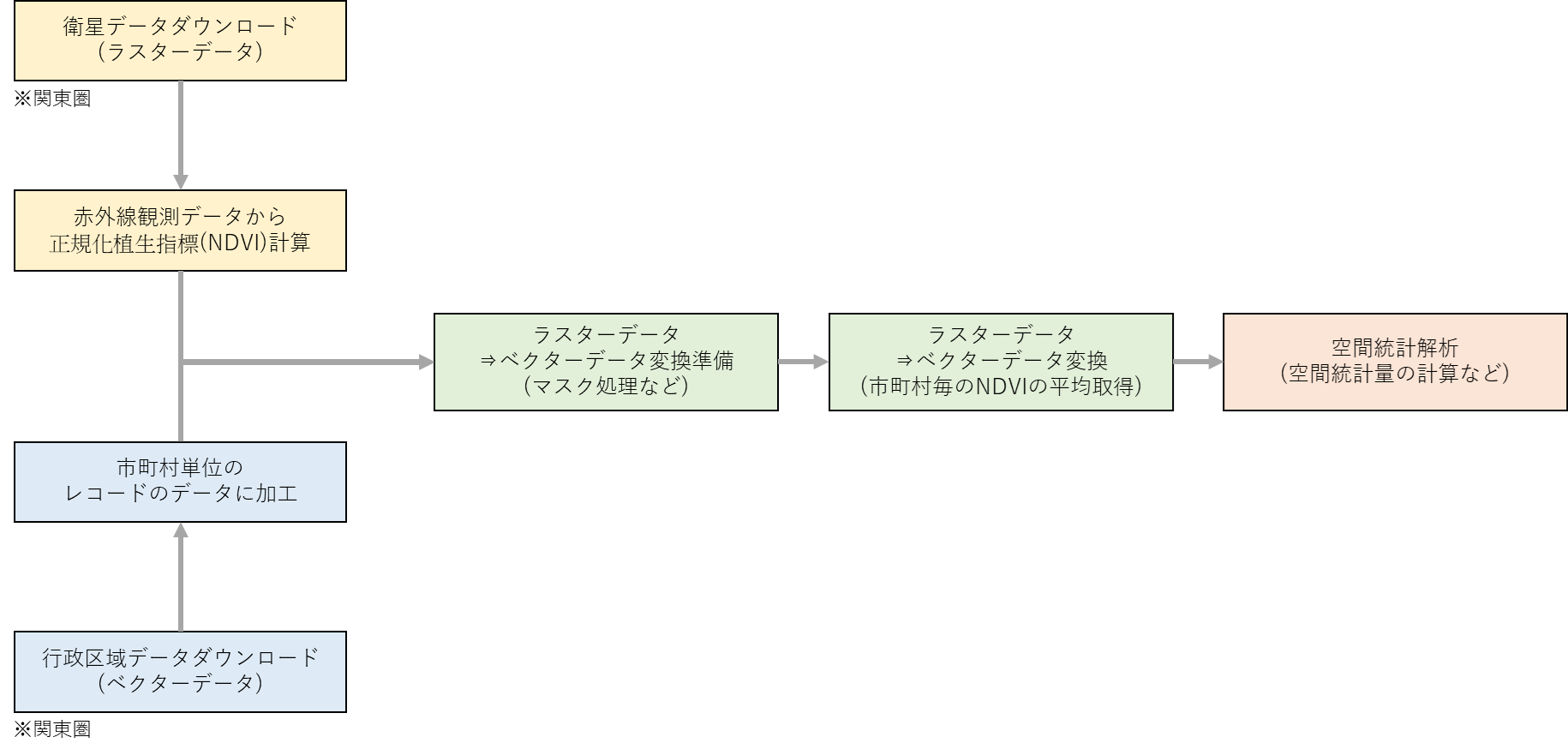
image.png

※Pythonで地理空間データの解析をした記事はこちら
衛星データでつくばみらい市の変化を見てみた（地理空間データ解析）

参考

先に参考にした本やサイトを書いておく。

使用言語・作業環境・使用ライブラリ

  • 言語：R
    普段はpython使っている人間だが今回は本に倣ってRを使用。正直あまり自由自在には扱えない。Anaconda公式の方法では古いバージョンのRしか使えないらしいので、condaでr-baseをinstallした。

  • 作業環境：JupyterLab
    RといえばRStudioでしょって思ったけど、Jupyterのほうが慣れ親しんでいるので…。devtools::install_github("IRkernel/IRkernel")でIRkernelを入れたらJupyterLabでもRを使えた。

  • 使用ライブラリ
    データハンドリングや地理空間データのためのライブラリを使用。

install.packages("tidyverse")
install.packages("rgdal")
install.packages("spdep")
install.packages("NipponMap")
install.packages("sf")
install.packages('raster')
install.packages("here")
install.packages("jpmesh")
install.packages("devtools")
install.packages("rmapshaper")
install.packages("geojsonio")
devtools::install_github("uribo/jpndistrict")
install.packages('maptools')

データダウンロード

衛星データ

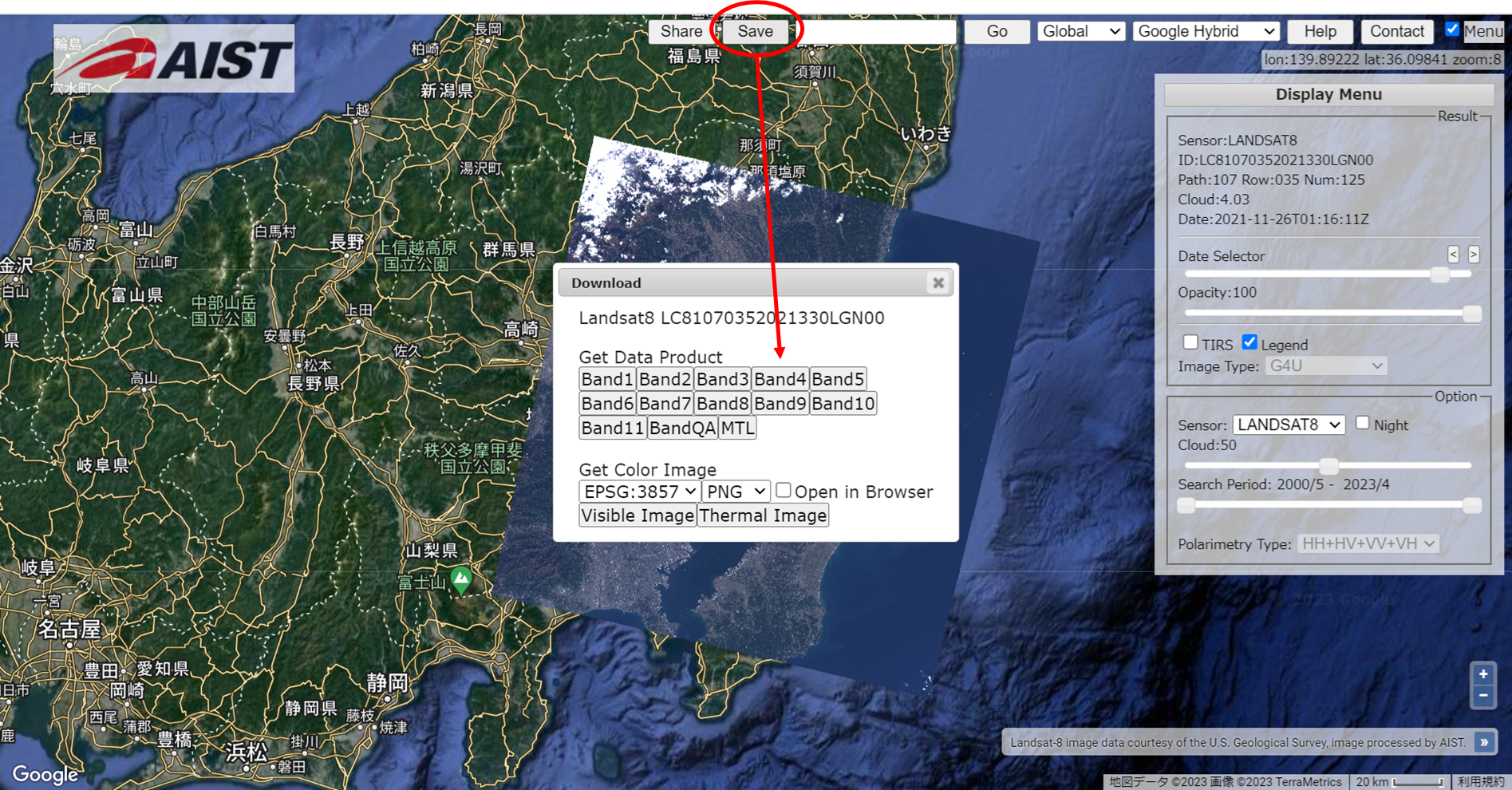
Fusic Tech Blog：LANDSAT-8の画像でNDVIを計算して可視化してみる(衛星データ活用)を参照。
この技術ブログでは衛星データを取得してNDVIまで計算しているので大いに参考にさせてもらった。
USGSでアカウントを作ってLandbroserで関東圏の衛星データをダウンロードした。
衛星はLANDSAT-8で、20210806-20210811のBand4とBand5のデータをダウンロードした。(TIFデータ)

ある日付の関東圏のデータ表示。
image.png
そしてデータダウンロード
image.png
image.png

行政区画データ

国土数値情報ダウンロードサイト 行政区域データから2022年の東京、神奈川、埼玉、千葉、茨城、栃木、群馬のデータをダウンロード。(shpファイルなど)
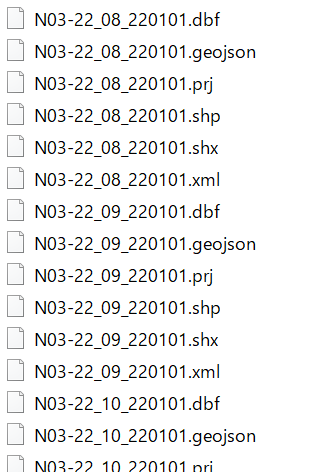
image.png
image.png

これでデータの準備は整った。

衛星データ読み込みからNDVI計算まで

NDVI計算まで実施していく。

ライブラリインポート。

library(sf)
library(rgdal)
library(spdep)
library(NipponMap)
library(RColorBrewer)
library(raster)
library(tidyverse)
library(jpmesh)
library(rmapshaper)
library(geojsonsf)
library(maptools)

TIFファイルリスト取得。RasterStackクラス作成。

ddir <- 'data/'
# ファイルリスト
tif_202108 <- list.files(ddir
                         , pattern = "LC08_L1TP_107035_20210806_20210811_02_T1.+.TIF"
                         , full.names = TRUE)
# Band4,5をまとめてRasterStackクラスにする
tif_202108 <- stack(c(tif_202108[1], tif_202108[2]))
slotNames(tif_202108)  # 読み込んだラスタオブジェクトのスロット名を確認
tif_202108

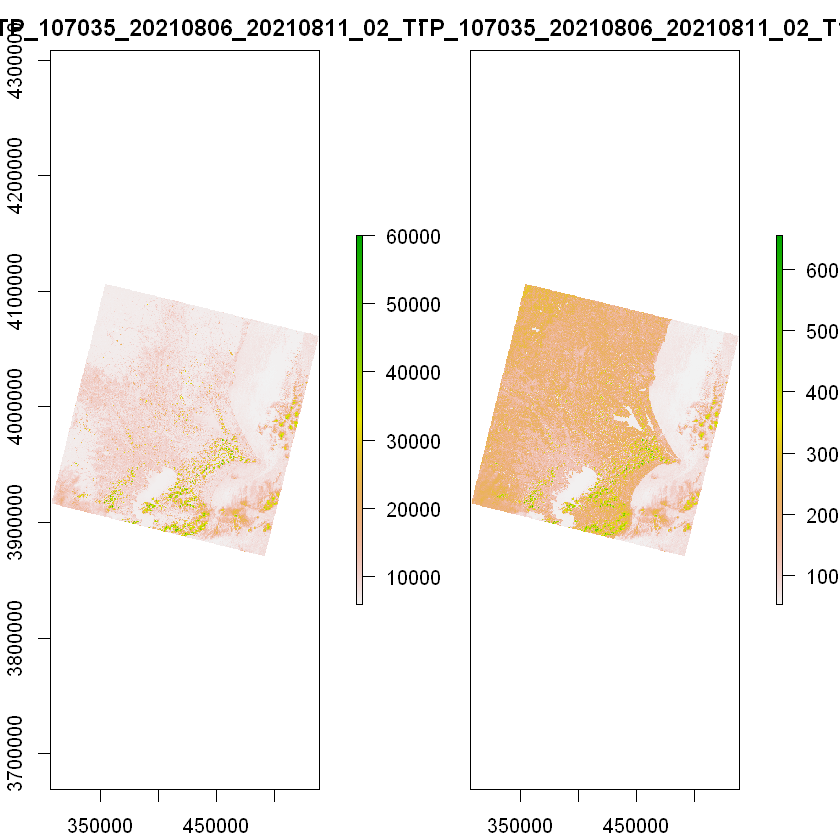
image.png

プロットしてみる。

plot(tif_202108)

左がBand4で右がBand5(だと思う)。
image.png

座標変換

今座標系がWGS84(世界測地系1984)なので日本でよく利用される空間座標系に変換する。
日本測地系2011（JGD2011）の平面直角座標系epsg:6677に変換する。
あまり詳しくないのだが、EPSGコードとは｜コードの定義情報・検索方法によると、

EPSGコードとは、GISで使用される様々な要素に必要なパラメータを1つにまとめ、そのパラメータの集合体どうしを区別するためにコードを割り振ったコード体系のことです。

ということらしい。

そしてepsg:6677は関東圏を中心とした座標系ってことかな。おそらく本来球なのに平面直角座標系にすることで歪みが発生するので、地域ごとに中心とした座標系が分かれているのかなと想像(歪むと面積とか計算できないし)。
EPSGコード一覧表/日本でよく利用される空間座標系（座標参照系）より
image.png

ということで座標系変換。

tif_202108trans <- tif_202108
tif_202108trans<-projectRaster(tif_202108trans, crs=CRS("+init=epsg:6677"))  # 座標変換
crs(tif_202108)
crs(tif_202108trans) <- CRS("+init=epsg:6677")  # crs情報を書き換え
cat("------")
crs(tif_202108trans)

元のデータのcrs情報（WGS84）
image.png
変換してcrs情報書き換え（epsg:6677）
image.png

プロットすると確かに座標が変わっている。

plot(tif_202108trans)

image.png

NDVI計算

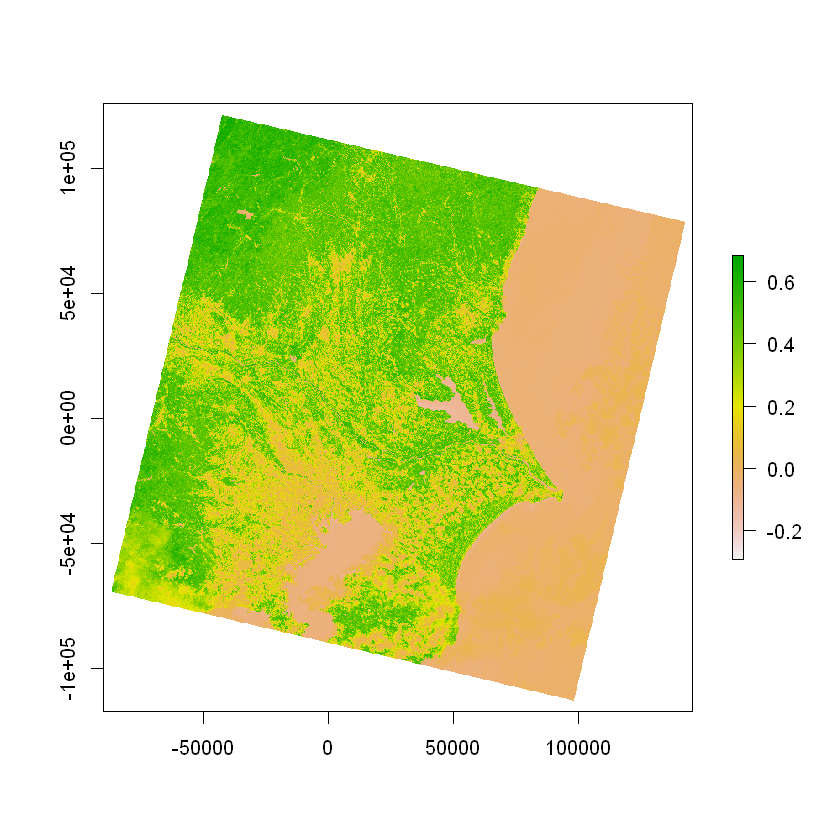
座標変換も終わったのでNDVIを計算してプロット。
緑が濃いほど植生が濃いと言える。

#NDVIを計算する関数
calc_NDVI <- function(img, n, r) {
  red <- img[[r]]
  nir <- img[[n]]
  return ((nir-red) / (red + nir))
}

#NDVIを計算する。NIR = 2, red = 1
ndvi <- calc_NDVI(tif_202108trans, 2, 1)
plot(ndvi)

# ggplotバージョン
#library(ggplot2)
#ndvi.df <- as.data.frame(rasterToPoints(ndvi))
#g <- ggplot(ndvi.df, aes(x=x, y=y)) + geom_tile(aes(fill = layer)) + coord_equal()
#print(g)

image.png

行政区画データ読み込みから市町村単位のレコードに加工するまで

まずshpファイルリスト取得。

# shapeファイルリスト
shplists <- list.files(ddir, pattern = "*_220101*.shp", full.names = TRUE)

１番目のshapeファイルを読み込む。（茨城県）

# １番目のshapeファイルを読み込む。（茨城県）
prefs <- st_read(shplists[1])
prefs <- prefs %>% filter(!N03_004 %in% c("大島町", "利島村", "新島村", "神津島村", "三宅村", "御蔵島村", "八丈町", "青ヶ島村", "小笠原村", "所属未定地"))  # 島などは除外
prefsTr <- st_transform(prefs, crs=6677)
prefsTr

1番目のファイルに2番目以降のファイルをつなげていく(ただ縦につなげるだけ)。

# ２番目以降のshapeファイルを読み込み、マージする。（茨城県以外の関東地方都県）
for (i in shplists[-1]){
    s.sf0 <- st_read(i)
    s.sf0 <- s.sf0 %>% filter(!N03_004 %in% c("大島町", "利島村", "新島村", "神津島村", "三宅村", "御蔵島村", "八丈町", "青ヶ島村", "小笠原村", "所属未定地"))  # 島などは除外
    s.sf0 <- st_transform(s.sf0, crs=6677)
    #属性データは県名市名行政区域コードを残す
    prefsTr<-rbind(prefsTr[,c('N03_001','N03_004', 'N03_007')], s.sf0[,c('N03_001','N03_004', 'N03_007')])
    print(unique(s.sf0$N03_001))
}
prefsTr

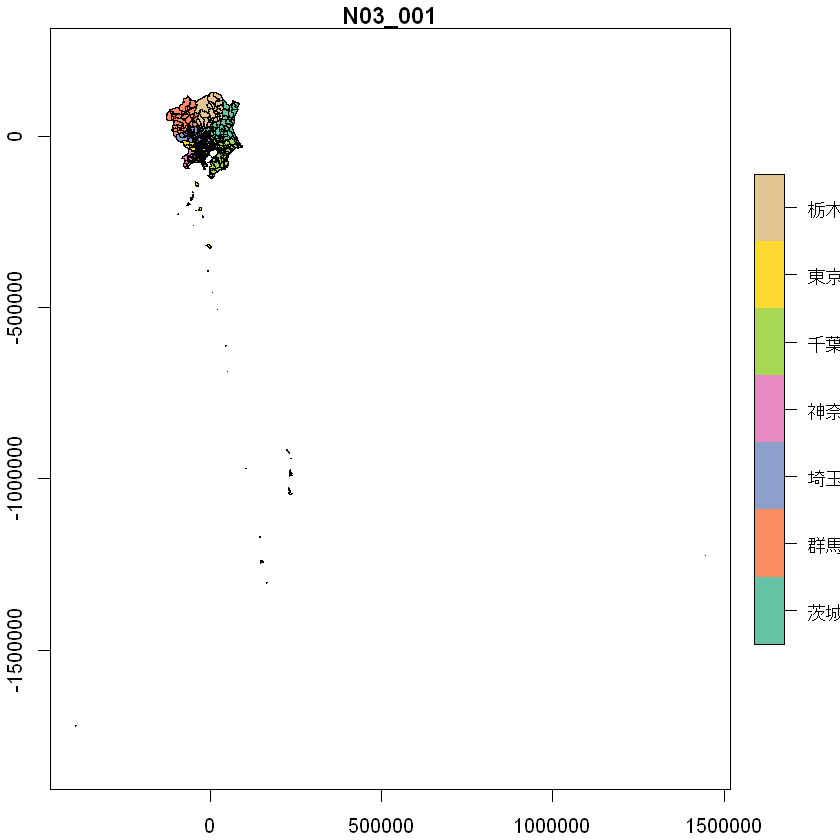
image.png

プロット。（島嶼部とかは抜いてたはずなんだが…。多分、各都・県全体を表してる行が存在しているっぽい。要はかなりでかいPolygonの行が含まれているような気がする。）

# shpファイルplot
plot(prefsTr[,'N03_001'], axes=T)
# ggplotの場合
#ggplot(prefsTr[,'N03_001']) + geom_sf()

image.png

市町村単位にまとめる

データの読み込みに成功したが、このデータは市町村が最小単位になっているわけではない。
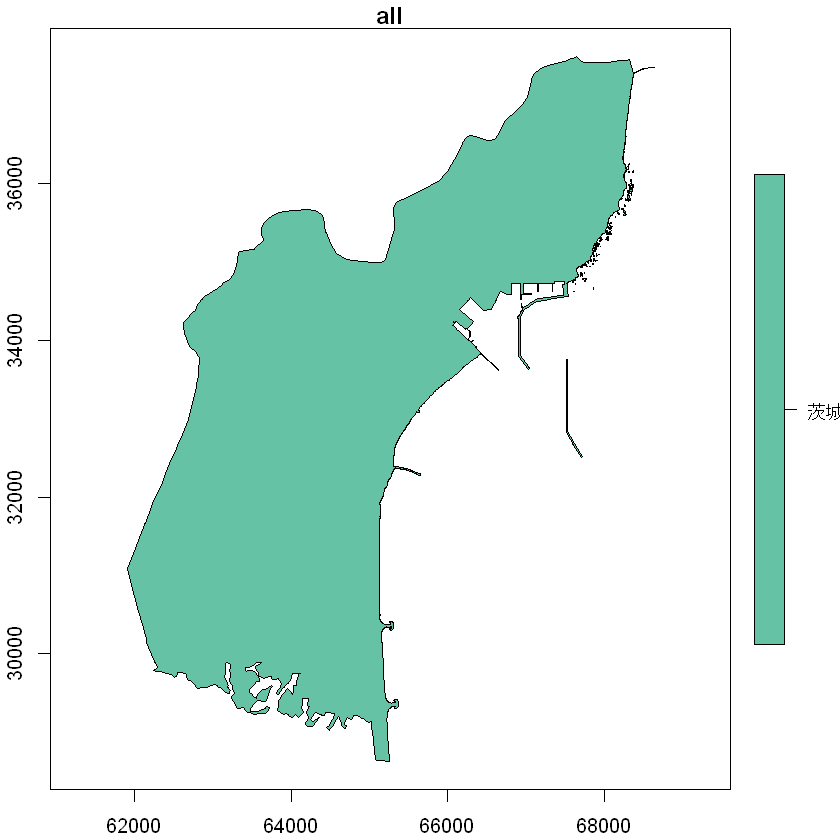
例えば茨城県大洗町のレコードを抜き出すと99レコードある。
99レコード分すべてをプロットすると大洗町全体となる。

# 大洗町も複数のレコードに分かれている
prefsTr_org2 <- (prefsTr_org %>% filter(N03_004 %in% c('大洗町')))
prefsTr_org2
plot(prefsTr_org2[,'N03_001'], axes=T, main='all')

image.png
image.png

この99レコードを1つずつプロットすると、一部細かいエリアがプロットされる。

# 97,98,99番目のレコードをプロット
for (i in (nrow(prefsTr_org2)-3):(nrow(prefsTr_org2)-1)) {
    plot(prefsTr_org2[i:i+1,'N03_001'], axes=T, main=i)#, add = T
}

97,98は細かいエリア。99は大洗町全体に見えるが、細かい部分が無い。
image.png

要は大洗町の例でいうこの99レコードを1つにまとめて1レコードにすることができればいい。

これはgroup_byを使えば容易くできる。
市町村単位でgroup_byしてsummariseすることで分割されていた市町村が統合される。
もともと4000行以上のレコードがあったが、まとめたことで351行のレコードとなる。

# 元データは残しておく
prefsTr_org <- st_as_sf(prefsTr)  # data.frameからsfクラスのデータを作成(念のため)
prefsTr_org$pref_city <- paste(prefsTr_org$N03_001, '_', prefsTr_org$N03_004)  # 県名＋市名

# 市町村単位のレコードにする
prefsTr <- st_as_sf(prefsTr)  # data.frameからsfクラスのデータを作成(念のため)
# 市町村単位でgroup_byしてsummariseすることで分割されていた市町村が統合される
prefsTr <- prefsTr %>% group_by(N03_001,N03_004) %>% summarise()
prefsTr$AREA <- prefsTr %>% st_area() %>% as.numeric()  # 市町村の面積
#prefsTr <- prefsTr %>% group_by(N03_001, N03_004) %>% slice_max(order_by = AREA, n = 1)
prefsTr$pref_city <- paste(prefsTr$N03_001, '_', prefsTr$N03_004)  # 県名＋市名
prefsTr

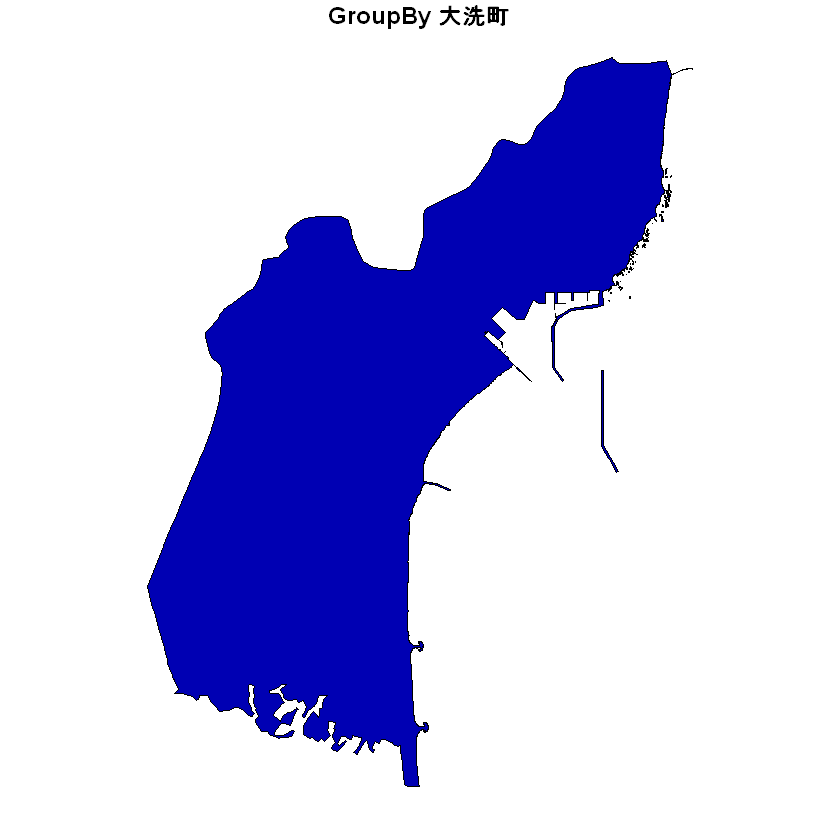
image.png

大洗町で元のデータと、市町村単位のレコードにしたあとのデータを比較。
大丈夫そう。

# 元のデータ
plot((prefsTr_org %>% filter(N03_004 %in% c('大洗町')))[,'N03_004'], main=paste('Original','大洗町'))
# 市町村単位のレコードにしたあとのデータ
prefsTr2 <- (prefsTr %>% filter(N03_004 %in% c('大洗町')))
plot(prefsTr2[,'AREA'], main=paste('GroupBy','大洗町'))

image.png
image.png

ラスター⇒ベクター変換準備

ベクターデータを使用したラスターデータの切り落とし(crop)とマスク(mask)を実施する。
2つの関数crop()とmask()は、ほとんどの場合で一緒に使う。
(a)ラスタの範囲を目的の領域に限定し、(b)領域外の値をすべてNAに置き換える、という処理をしている。

(a)：
crop()を使うと、ラスターをベクターに合わせて切り出すことができる。
※とはいっても今回のベクターデータの範囲内にラスターデータの範囲は内包されているので、ラスターデータがどこか欠如することは無い。ラスターデータの範囲が広くてベクターデータの範囲が狭いときは必須かと。

# NDVIラスタとシェープファイルベクターをオーバーレイ
croped<-crop(ndvi, prefsTr[,'pref_city'])
plot(croped)
plot(prefsTr[,'pref_city'], borders="white", col=NA, add=T)

image.png

(b)：
次はマスク処理。mask()は第2引数にshpファイルを渡すと境界外のラスターデータの値をNAに設定する。
なので関東圏の外側のすべてのセルをマスクすることになる。

start <- proc.time()
#処理範囲をマスクする
masked<-mask(croped, prefsTr)
proc.time()-start

けっこう時間がかかったので保存しておく。

writeRaster(masked, 'output/masked.tif', overwrite=TRUE)

image.png

プロットして確認。海上のラスターデータの値がマスクされた。

#表示して確認
plot(masked)
plot(prefsTr, borders="white", col=NA, add=T)

image.png

ベクターデータの方に欠損行もあるので、欠損行も削除しておく。
欠損行は市町村名の列がNAになっている行で、面積がかなり大きいのでおそらく各都・県全体を表してる行ではないかと思っている。↓

# 東京都で市町村がNAの行をプロット
prefsTr[187,]
plot(prefsTr[187,'N03_001'])

image.png

欠損行削除でベクターデータの島嶼部などを含むPolygonが除外され、351行のデータが344行のデータになる。

# 欠損行削除
prefsTrnonNan <- na.omit(prefsTr)  # 島嶼部などを含むPolygonが除外される
cat('length', length(prefsTr), '\n')
cat('ncell', ncell(prefsTr), '\n')
cat('nrow', nrow(prefsTr), '\n')
cat('ncol', ncol(prefsTr), '\n')
cat("------", '\n')
cat('length', length(prefsTrnonNan), '\n')
cat('ncell', ncell(prefsTrnonNan), '\n')
cat('nrow', nrow(prefsTrnonNan), '\n')
cat('ncol', ncol(prefsTrnonNan), '\n')
prefsTrnonNan

image.png

島嶼部などを含むPolygonが除外されていることがわかる。

# ベクター欠損行削除後(ラスター on ベクター)
plot(st_geometry(prefsTrnonNan))
plot(masked, add=T)

image.png

ラスター⇒ベクター変換

raster::extract()を使うことで、ラスターデータからベクターデータの位置にある値を抽出できる。
Polygonのベクターデータがある場合、Polygon内のラスターデータの平均値を計算したりできる。
全領域にラスターデータの値が無い市町村については、値があった部分だけで平均が取られている。（千葉の南や群馬のあたり）

start <- proc.time()
#prefsTrnonNan <- as(prefsTrnonNan, "Spatial") # sf オブジェクトを sp へ
maskedex = raster::extract(masked, prefsTrnonNan, fun=mean, na.rm = TRUE)  # Rasterオブジェクトから平均値を抽出
prefsTrnonNanex <- prefsTrnonNan
prefsTrnonNanex$ndvi <- maskedex
prefsTrnonNanex <- st_as_sf(prefsTrnonNanex)  # data.frameからsfクラスのデータを作成
proc.time()-start
# 保存
st_write(prefsTrnonNanex, 'output/prefsTrnonNanex.shp', layer_options = "ENCODING=CP932", append=FALSE)

image.png

さて、これでラスターデータをベクターデータに変換(Polygonごとの平均値)できたのでプロットしてみる。
NaNのPolygonもあるのでNaNを消したバージョンもプロットしてみる。

# plotのカラースケール
nc <- 11
breaks <- seq(min(prefsTrnonNanex$ndvi %>% na.omit()), max(prefsTrnonNanex$ndvi %>% na.omit()), length.out = nc+1)
# cmap
pal <- (brewer.pal(n=nc, name="RdYlGn")) # 色逆パターンがrev(brewer.pal(n=nc, name="RdYlGn"))
nvdiNonnan <- prefsTrnonNanex %>% na.omit()  # NaNのPolygonを消す
plot(prefsTrnonNanex[, 'ndvi'], pal=pal, breaks=breaks)
plot(nvdiNonnan[, 'ndvi'], pal=pal, breaks=breaks)  # NaNのPolygonを消したバージョンプロット

image.png
(NaNのPolygonを消したバージョン)
image.png

緑がNDVIが高く、赤になるほどNDVIが低い。
これを見るだけで、東京周辺は植生が薄く、東京の西部、北関東の北部は植生が濃いことは明らか。
元のラスターデータとざっくり並べてみるとこんな感じ。
image.png

次は空間統計解析をやってみる。（やっと書籍の内容を実践できる）

空間統計解析

NDVIのベクターデータで空間統計を見ていく。
空間統計の説明は 「Rではじめる地理空間データの統計解析入門」から引用 していく。

空間相関と近接行列

空間相関

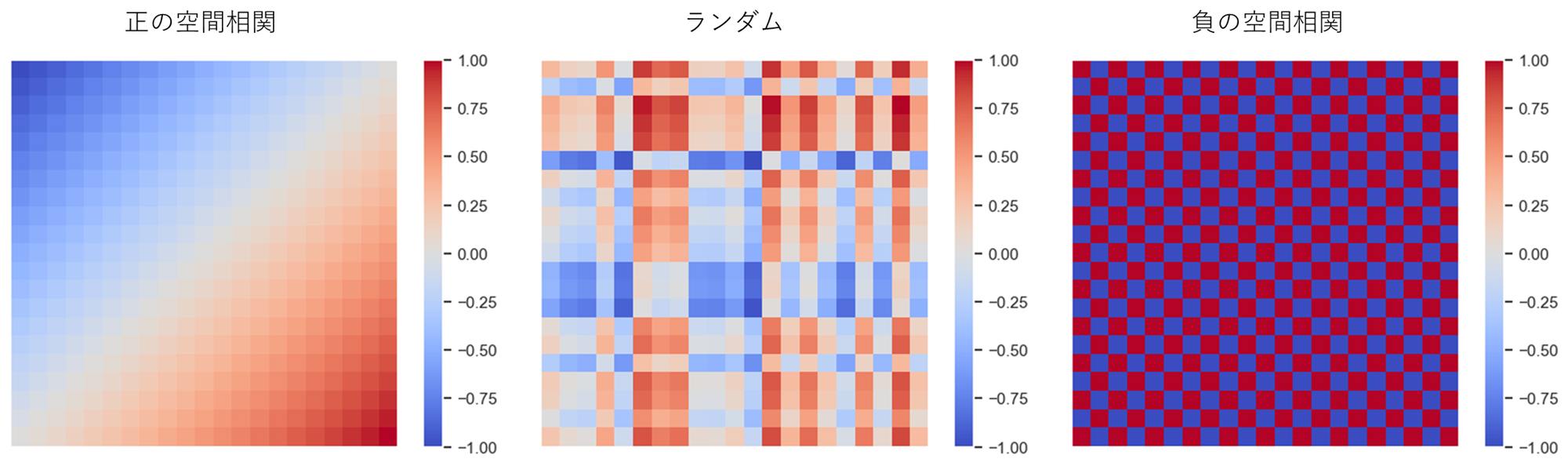
空間データの基本的な性質の一つに、「近所と相関関係を持つ」という空間相関がある。
空間相関には近所と似た傾向を持つという正の空間相関と、近所と逆の傾向を持つ負の空間相関がある。
空間データには多くの場合正の相関がある(駅に近いほど地価が高い、工場に近いほど地価が低いなど)。一方、負の相関は空間競争の結果として現れると言われている(大型ショッピングモールができると周辺の商店の売り上げが下がるなど)。
image.png

近所の定義

空間相関をモデル化するためには、近所を定義する必要がある。
近所の定義は例えば以下のようなものがある。

  • 境界を共有するゾーン(ルーク型; 縦横)
  • 境界または点を共有するゾーン(クイーン型; 縦横斜め)
  • 最近隣kゾーン
  • 一定距離以内のゾーン

今回は最近隣kゾーンを定義とする。
これは、例えば各ゾーンに地理的重心(役所とか代表点の位置座標)があるとすると、自分自身を含まない地理的重心間距離の近隣4ゾーン(k=4)を近所とする、というような定義である。

近接行列

このように近所を定義したとして、それをデータとしてはどう表すかというと、近接行列を使う。
ゾーン$i$と$j$の近さ$ω_{i,j}$を第$(i,j)$要素を持つ行列を近接行列と呼ぶ。
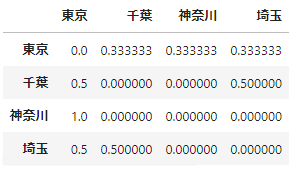
東京、神奈川、埼玉、千葉の4都県の近接性を上下左右(ルーク型)と定義すると近接行列は以下のようになる。
image.png
同一ゾーン内の空間相関は考慮しないこととするので、対角要素は0になる。

近接行列は行基準化されることもあるので、その時は以下のような近接行列になる。
image.png

今回のベクターデータで最近隣4ゾーンを近隣とした近接行列を視覚化してみると以下のようになる。

coords <- st_coordinates(st_centroid(nvdiNonnan)) # 重心確認
knn <- knearneigh(coords,4) # 最近隣4ゾーン
nb2 <- knn2nb(knn) # nb形式
w <- nb2listw(nb2) # listw
plot(st_geometry(nvdiNonnan), col='white')
plot(nb2, coords, add=TRUE, col='red', cex=0.5, lwd=2.)

image.png
わかりにくいが、各市町村の地理的重心から4本の線が出ている。この線でつながっているほかの市町村が近隣市町村ということになる。
このように近所を定義することによって空間相関を評価することができる。

大域空間統計量

空間相関の評価には、標本全体に対する空間相関の強さを評価する 大域空間統計量 とゾーンごとの局所的な空間相関の強さを評価する 局所空間統計量 がある。
まずは大域空間統計量から見ていく。

モランI統計量

モラン$I$統計量はN個のゾーンで区切られたデータ$y_1, …, y_N$の空間相関を評価する指標。

I=\frac{N}{\sum_{i}\sum_{j}ω_{ij}}\frac{\sum_{i}\sum_{j}ω_{ij}(y_{j}-\bar{y})(y_{i}-\bar{y})}{\sum_{i}(y_{i}-\bar{y})^2}

$\bar{y}$は標本平均。$ω_{i,j}$は近接行列の第$(i,j)$要素であり、ゾーン$i$と$j$の近さを表す既知の重み。
自ゾーン$(y_{i}-\bar{y})$と近隣$(\sum_{j}ω_{ij}(y_{j}-\bar{y}))$との相関の強さを表す指標となる。
$I$が正の方向に大きいと正の相関、負の方向に大きいと負の相関があることを意味する。

近接行列を定義して、NDVIの大域的な空間相関を調べてみる。
spdepのmoran.test()ですぐにできる。alternative = "greater"で正の相関の片側検定、alternative = "less"で負の相関の片側検定ができる。

# 近接行列定義
coords <- st_coordinates(st_centroid(nvdiNonnan)) # 重心確認
knn <- knearneigh(coords,4) # 最近隣4ゾーン
nb2 <- knn2nb(knn) # nb形式
w <- nb2listw(nb2) # listw
pop <- c(nvdiNonnan$ndvi)

# モラン統計量
moran <- moran.test(pop, listw = w)
moran
moran <- moran.test(pop, listw = w, alternative = "less")
moran

image.png
$I$は0.829となっており、正の空間相関の片側検定でp値が-16乗のオーダーとなっているので、NDVIは関東圏において正の空間相関があるといえる。一方、負の相関の片側検定ではp値が1となっており統計的に有意な負の空間相関があるとは言えないこととなる。
NDVIのベクターデータプロットを見ると、東京周辺では植生が薄く東京から離れた北関東方面では植生が濃くなるなど、確かに正の空間相関はありそうで直感に合う。

G*統計量

空間的な集積(値がある特定の地域に集積しているか否か)の指標として$G$統計量がある。

G=\frac{\sum_{i}\sum_{j}ω_{ij}y_{i}y_{j}}{\sum_{i}\sum_{j}y_{i}y_{j}}

$G$統計量は、例えば人口、売上高、患者数といった非負の観測値に対する統計量。
$G$は0以上の値をとり、その値が小さいことは観測値がランダムな空間分布を持つことを意味し、逆に大きいことは大きな観測値が特定の地域に集中していることを意味する。
$G$統計量は、自ゾーンの観測値を無視した(近接行列の対角成分は0)指標なので空間的な集積の解釈が難しい面がある。
そこで自ゾーンと近隣の両方を考慮した空間集積の統計量として$G^{＊}$統計量が用いられてきた。

G^{＊}=\frac{\sum_{i}\sum_{j}ω_{ij}^{＊}y_{i}y_{j}}{\sum_{i}\sum_{j}y_{i}y_{j}}

$ω_{ij}^{＊}$は$i=j$の場合1、それ以外の時は$ω_{ij}$となる。(要するに対角成分が1の近接行列)

$G^{＊}$統計量の評価もspdepのglobalG.test()を使えば簡単にできる。
NDVIは負の値も取り得るので$G^{＊}$統計量を求めるのは違う気がするが、今回負の値なさそうだしいいかなって思って実施。

# G*統計量
# G*統計量は空間集積の検定統計量(空間的に偏っているか)
# include.self関数は対角項を1に
w_b <- nb2listw(include.self(nb2), style='B') # 対角成分が1の近接行列
Gstar <- globalG.test(pop, listw=w_b)
Gstar
Gstar <- globalG.test(pop, listw=w_b, alternative = "less")
Gstar

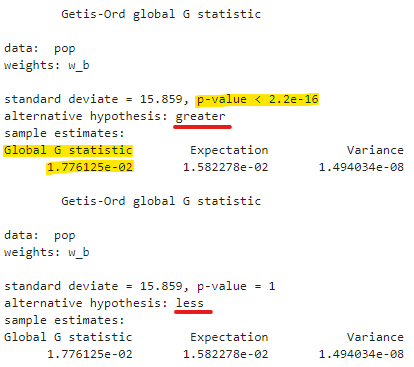
image.png
alternative = "greater"で帰無仮説を「空間集積が存在しない」とした片側検定、alternative = "less"で帰無仮説を「空間集積が存在する」とした片側検定ができる。
今回のNDVIでは、p値が-16乗のオーダーとなり帰無仮説「空間集積が存在しない」が棄却され、統計的に有意な空間集積が存在することが確認できた。
これもモラン$I$統計量の時と同様NDVIのベクターデータプロットを見ると、東京から離れた北関東方面(特に北部)で植生が濃くなるなど、確かにNDVI値がある特定の地域に集積していそうなので直感に合う。

局所空間統計量

局所空間統計量(LISA)は各ゾーン周辺の局所的な空間特性を評価するための統計量。
大域所空間統計量(GISA)とは以下の関係がある。

GISA=\frac{1}{N}\sum_{i=1}^N{LISA_i}

つまり大域空間統計量をゾーンごとに分解したものが局所空間統計量である。
なので今回の場合は各市町村ごとに局所空間統計量が求められるので、プロットすることでどの市町村に正の相関がありそうか、などを分析することが可能になる。
ということで局所モラン$I$統計量と局所$G^{＊}$統計量を求めてみる。

局所モランI統計量

I_i=\frac{1}{m}(y_{i}-\bar{y})\sum_{j}ω_{ij}(y_{j}-\bar{y})

$m(=\frac{1}{n-1}\sum_{i=1,i{\neq}j}^{I}(y_{i}-\bar{y})^{2}-\bar{y}^{2})$は、$I$を分解した過程で現れる定数。
$I_i$は自分と周辺の相関に着目した指標で、自分の周辺が似た傾向を持つ(正の空間相関)場合は正、逆の傾向を持つ(負の空間相関)場合は負になる。
局所モラン$I$統計量はspdepのlocalmoran()関数ですぐに出せる。

# 局所モランI統計量
lmoran <- localmoran(pop, listw = w)
lmoran[1:5,]

image.png

NDVIのsf dataframeに局所モラン$I$統計量の列を追加。

# 列追加
nvdiNonnan$lmoran <- lmoran[,"Ii"]  # local moran statistic
nvdiNonnan[,"lmoran"][1:5, ]

image.png

局所モラン$I$統計量をプロットする。

# plotのカラースケール
maxval <- max(nvdiNonnan$lmoran) #max(max(nvdiNonnan$lmoran), abs(min(nvdiNonnan$lmoran)))
minxval <- min(nvdiNonnan$lmoran) #-1*max(max(nvdiNonnan$lmoran), abs(min(nvdiNonnan$lmoran)))
step <- (maxval-minxval) / 9 #(maxval)*2 / nc
breaks <- seq(from = minxval
              , to = maxval
              , by = step)
# cmap
pal <- (brewer.pal(n=9, name="OrRd")) # 色を逆パターンがrev
# nvdiNonnanはshapeファイルなのでplotで自動的に日本地図のようにplotされる)
plot(nvdiNonnan[,"lmoran"], pal=pal, breaks=breaks)

image.png
東京周辺、東京の西部、北関東の北部の局所モラン$I$統計量の値が大きい。
東京周辺では自身の植生が薄いと近隣の植生も薄い、東京の西部、北関東の北部では自身の植生が濃いと近隣の植生も濃いという意味で正の空間相関があるといえる。

各市町村ごとに局所モラン$I$統計量の統計的有意性を確認するためにp値をプロットする。
濃い紫が1%水準、濃い紫が10%水準で有意であるという見方。

# 局所モランIのp値
nvdiNonnan$lmoran_p <- lmoran[,"Pr(z != E(Ii))"]  # local moran statistic
# plotのカラースケール
breaks <- c(0, 0.01, 0.05, 0.1, 1)
nc_p <- length(breaks) - 1
# cmap
pal <- rev(brewer.pal(n=nc_p, name="RdPu")) # 色を逆パターンがrev
# nvdiNonnanはshapeファイルなのでplotで自動的に日本地図のようにplotされる)
plot(nvdiNonnan[,"lmoran_p"], pal=pal, breaks=breaks)

image.png
都心～川崎あたり、東京の青梅市より西部、茨城のひたちなか市より北部、栃木の宇都宮市より北部、群馬の前橋市より北部において、1%水準で統計的に有意であり正の空間相関が見られる。
都心においては植生の薄さに空間相関があり、都心から離れるにつれ植生の濃い薄いにおいて空間的な相関はなくなるが、さらに離れていった先、例えば北関東の県庁所在地を過ぎた先では植生の濃さに空間相関が現れてくることがわかる。

また、局所モラン$I$統計量については、モラン散布図が出せる。
局所モラン$I$統計量の式から、以下のことが考えられる。

  • 自分も周辺も平均以上($I_i$は正)
    • $y_{i}-\bar{y}>0$かつ$\sum_{j}ω_{ij}(y_{j}-\bar{y})>0$
  • 自分も周辺も平均以下($I_i$は正)
    • $y_{i}-\bar{y}<0$かつ$\sum_{j}ω_{ij}(y_{j}-\bar{y})<0$
  • 自分は平均以上、周辺は平均以下($I_i$は負)
    • $y_{i}-\bar{y}>0$かつ$\sum_{j}ω_{ij}(y_{j}-\bar{y})<0$
  • 自分は平均以下、周辺は平均以上($I_i$は負)
    • $y_{i}-\bar{y}<0$かつ$\sum_{j}ω_{ij}(y_{j}-\bar{y})>0$

つまり$y_{i}-\bar{y}$と$\sum_{j}ω_{ij}(y_{j}-\bar{y})$に基づいて4分割できる。
横軸を$y_{i}-\bar{y}$、縦軸を$\sum_{j}ω_{ij}(y_{j}-\bar{y})$として散布図を描くと、周辺に対して突出して高い/低い、周辺も自分も高い/低いゾーンを確認することができる。これをモラン散布図という。
moran.plot()ですぐにモラン散布図は出せる。

# moran散布図
moran.plot(pop, listw = w, labels = nvdiNonnan$pref_city, pch=20)

image.png
モラン散布図を見ると、自分だけが高い(植生が周辺に比べて濃い)市町村はあまり無さそう。
強いて言えば、埼玉県さいたま市の西区と緑区は大宮や川口市に隣接しており、そこに比べると植生は濃い方であるので、散布図ではやや右下に寄っている。
自分だけが低い(植生が周辺に比べて薄い)市町村はいくつか見られて、例えば埼玉県鶴ヶ島市は周辺に比べて植生が薄い。
埼玉県鶴ヶ島市についてなぜ周辺より植生が薄いのかはちょっとわからなかった…。
ChatGPTさんにも聞いてみたが、比較的発展しているところなのだろうか。
image.png

NDVIのベクターデータプロットで、上で挙げた埼玉県さいたま市の西区と緑区、埼玉県鶴ヶ島市を見てみると、確かに周辺より濃かったり薄かったりしていることは確認できた。
image.png

局所G*統計量

最後、局所$G^{＊}$統計量についても見てみる。（※NDVIは負の値も取り得るので局所$G^{＊}$統計量を求めるのは違う気がするが、今回負の値なさそうだしいいかなって思って実施。）
$G_{i}^{＊}$の式は以下。

G_{i}^{＊}=\frac{\sum_{j}ω_{ij}^{＊}y_{j}}{\sum_{i}y_{i}}

局所$G^{＊}$統計量もlocalG()関数ですぐ出せる。ただ、localG()関数は局所$G^{＊}$統計量そのものではなく、「空間集積は存在しない」という帰無仮説の下で評価した局所$G^{＊}$統計量の$z$値が出力される。
これをプロットすると、空間集積がどのあたりで起きているのかわかる。

# ローカルG*統計量
# G*統計量は空間集積の検定統計量(空間的に偏っているか)
# include.self関数は対角項を1に
w_b2 <- nb2listw(include.self(nb2)) # 近接行列
# Local G*
lG <- localG(pop, listw = w_b2)
# 可視化
nvdiNonnan$lG <- lG

#maxval <- max(max(nvdiNonnan$lG), abs(min(nvdiNonnan$lG)))
#minxval <- -1*max(max(nvdiNonnan$lG), abs(min(nvdiNonnan$lG)))
#step <- (maxval)*2 / nc
#breaks <- seq(from = minxval
#              , to = maxval
#              , by = step)

# cmap
breaks <- c(-5, -2.58, -1.96, -1.65, 0, 1.65, 1.96, 2.58, 5)  # z値の有意水準10,5,1%の臨界値
pal <- rev(brewer.pal(n=length(breaks)-1, name="RdBu")) # 色を逆パターンがrev
graphics::plot(nvdiNonnan[,"lG"], pal=pal, breaks=breaks)

image.png

局所モランの時の正の空間相関がある場所と同じで、東京周辺、東京の西部、北関東の北部あたりで空間集積があることがわかる。

おわりに

空間統計についてはまだまだいろいろ解析方法があるので、「Rではじめる地理空間データの統計解析入門」を読むと面白いと思う。今回やった内容は本当に序の口で、7部ある構成のうち2部までの内容なので。
今回の作業で実際時間がかかったのはラスターデータいじったり、ベクターデータいじったりしたところなので、今後はもう少し空間統計解析に時間を使っていきたいと思う。
あとpython使いなので、同じことをpythonでやったりもしたいな。
地理空間データ、おもろいやん！

以上！

3
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
4