https://deeplearningbook.org を読んでいて、6章で Universal Approximation Theorem (普遍性定理) なるものが出てきた。
今まで知らなかったのと、すごいなと思ったので理解したことをメモしておきます。
理解が甘いところもあると思うのでご指摘歓迎です。
- Universal Approximation Theorem とは
- 何にすごいと思ったのか
- 何ができるようになるか & 研究動向
Universal Approximation Theorem とは
In the mathematical theory of artificial neural networks, the universal approximation theorem states that a feed-forward network with a single hidden layer containing a finite number of neurons (i.e., a multilayer perceptron), can approximate continuous functions on compact subsets of Rn, under mild assumptions on the activation function. The theorem thus states that simple neural networks can represent a wide variety of interesting functions when given appropriate parameters; however, it does not touch upon the algorithmic learnability of those parameters.
One of the first versions of the theorem was proved by George Cybenko in 1989 for sigmoid activation functions.
要約すると、
Universal Approximation Theorem (日本語では"普遍性定理"と呼ばれる)は、有限個のユニットを持つ一層の隠れ層で構成されるfeed-forward networkは、いくつかの条件のもと、任意の連続関数を近似することが出来る、という定理。
言い換えると、feed-forward networksを使うことで適当な連続関数を近似できることが理論的に保証された、ということ。
どういうこと
機械学習であるタスクに取り組む時、基本的にはなんらかの入出力があるモデルを用意することを考える。
ここで、システムにあたる関数 f の真の形は知ることが出来ないとする。
この f に置き換わるような、新たに入力 x が与えられた時の出力 y を予測するようなモデル g を、データから学習することで構築するのが機械学習的アプローチにあたる。
gに当たるものは様々なものがあるが、その一つがニューラルネットワークになる。
ここで、「システムfを機械学習のモデルであるgでどのくらい近似することができるのか?」という疑問が出て来る。
例えば、真のシステムfが、その下記のように入力 $x$ に対して $e^{x} $ で与えられているとする。
f(x) = e^x \,\, (1)
これを $x∈[0,1]$ において、下記の多項式関数 g で近似することを考える。
g(x) = \sum_{k=0}^{n} a_{k} x^k \,\, (2)
式(1)は、テイラー展開により次のように多項式近似できる、すなわち多項式関数のモデルで表現できることが知られている。
f(x) = \sum_{k=0}^{\infty} \frac{x^k}{k!} = 1 +x+ \frac{x^2}{2!} + ... \,\,(3)
例えば $n=1$ のとき、 $g(x) = a_0 + a_1 * x$ となるが、これではたいした近似はできないことはわかりやすい。
では、たいした近似はできないというのは、どの程度の近似なら可能なのだろうか?
また、**nが大きな値となった時にどのくらいの近似が出来ているのだろうか?**ということが気になってくる。
ここで、上記例の多項式関数によるモデルの場合は、式(3)のkをある値で切った時の近似誤差は、テイラー展開の剰余項を計算することで定量的な評価ができる。
では、ニューラルネットワークによるモデルgで近似する場合は、元のシステムfをどのくらい表現することが出来るのか?
これを説明したのがUniversal Approximation Theoremであり、その答えが冒頭に述べた、有限個のユニットを持つ一層の隠れ層で構成されるfeed-forward networkは、いくつかの条件のもと、任意の連続関数を近似することが出来るというもの。
最初に発表された論文(G. Cybenko, Approximation by Superpositions of a Sigmoidal Function, Mathmatics of control, signal and systems, vol. 2, no. 4, 1989)では、activation functionにシグモイド関数のような性質を持つ関数を用いている。
イメージの理解
(元論文の証明とは違うため、あくまでイメージでの理解です)
単純なニューラルネットを考える。
このような標準的なネットワークについて、出力は下記のような非線形関数の線形和になっているとする。
y = \sum_{i=1}^{N} \alpha_i\sigma(w_i^\mathrm{T}x + b_i) \,\,(4)
ここで、σは下記で与えられるシグモイド関数とする。
\sigma(x) = \frac{1}{1+e^{-x}} \,\, (5)
イメージで理解するためには、activation functionがステップ関数だと仮定するとわかりやすい。
式(5)において、x → ∞とすることで、これはx = 0で発火するステップ関数とみなすことが出来る。
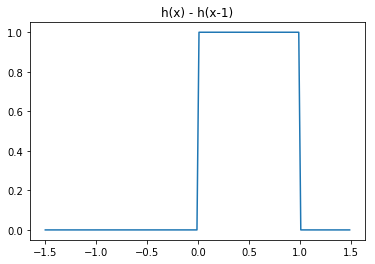
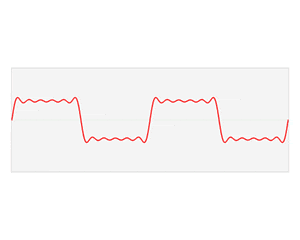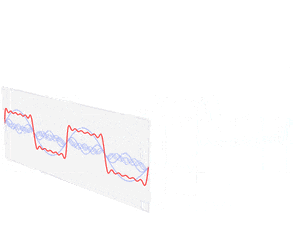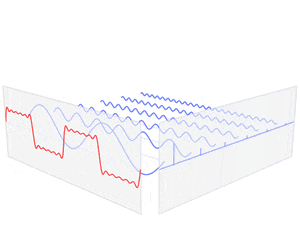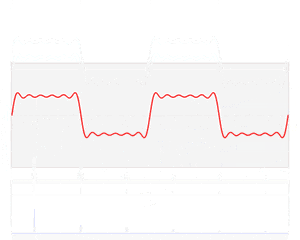
このステップ関数を h(x) とおくと、2つ組み合わせることで次のように任意の凸の形をした関数を作ることが出来る。
y = h(x) - h(x-1)
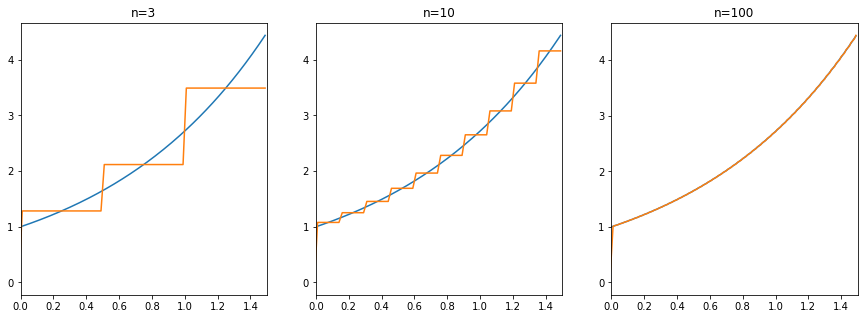
これを数を増やして組み合わせることで、様々な関数を表現することができる。式(1)をステップ関数で実現した例が下図である。
これで、近似誤差をユニットを増やすことで任意に減らすことができる(イメージ)。
フーリエ変換と似ていると思った。
画像はWikipediaより
ここまで行くと、元の関数を知ってれば誤差をなんとなく計算できそうで、ユニットを増やすとどのくらいのオーダーで誤差が減るか分かる。
何にすごいと思ったのか
ニューラルネットワーク(特にDeep Learning)に対する私の以前の印象
- モデルの表現力がめっちゃ高くてすごい
- 大量データから学習するため時間がかかる
- 中身がどうなっているか分からないため、職人的アプローチが必要になる
端的に言うとすごいんだけどブラックボックスという印象だった。
ところがどっこい、学習についてはともかく、理論上の表現性能についてはしっかり証明されている。
(もちろん学習についての研究もたくさん)
今まで何気なく使って何気なく良い性能が出てはいたが、これがあるおかげで"良い性能"の部分が理論的に保証され、気軽にニューラルネットワークによるモデル構築に取り組めるようになったということ!
更に言うと、土台of土台となる理論なので、ここから更によく見られるようなpracticalな手法についての理論を詰めていくことが出来る。
確率論の極限定理みたいなノリでテンション上がった。
何ができるようになるのか & 研究動向
最初に述べた通り、一層の隠れ層で構成されるようなfeed-forward networksを使うことで、適当な連続関数を近似できることが理論的に保証できるようになる。
もちろん、学習の最適化などの問題で、実応用上で適当な関数を完璧に再現できるわけではない。しかし、理論的にどのくらいのネットワークを作ればどの程度まで関数を近似することができるかが分かるようになった。
逆に言えば、下記のようなことが言える。
- 隠れ層のユニットを
n個にした時に、元の関数との誤差をL(n)で減らすことが出来る - 隠れ層の数を
m個にした時に、元の関数との誤差をL(m)で減らすことが出来る - 新しいネットワークを思いついた時に、この定理に基いてその表現力を議論することができる。
楽しそうですね。
いくつかさらった中で、既にこういうことは研究されているよという例を研究動向として並べておきます。
- A. R. Barron, "Universal approximation bounds for superpositions of a sigmoidal function," IEEE Transactions on Information theory, 1993
一層のfeed forward networkについて、n個のニューロンがあった時、二乗誤差は$O(1/n)$ になることを示した話。
(原論文には当たれなかったので、他の論文からの紹介引用)
- M. Telgarsky, "Benefits of depth in neural network", arXiv:1602.04485, 2016
難しくて分からないけど多分layerをdeepにした時に表現能力が指数的に上がっていくという話。
- S. Liang and R. Srikant, "Why deep neural networks for function approximation?," arXiv: 1610.04161, 2016
なぜDeep Learningにおいてshallow networksよりdeep networksの方が良いのか。
$\log(1/\epsilon)$個の層について、ニューラルネットワークが任意の連続関数を、各層で$O(poly \log(\epsilon))$ 個のパラメータでエラーバウンド$ε$で近似できることを示した話。
- O. Delalleau and Y. Bengio, "Shallow vc. deep sum-product networks," NIPS 2011
同じ誤差率を達成するのに、2層だと指数的に多くの数のユニットがいるが、3層だと多項式的な数のユニットで抑えられることを示したっぽい話。
この記事は以上です。
応用面が注目されがちのDeep Learningですが、理論面もどんどん新しい研究が進んでいて楽しそうでした。