アルゴリズムとデータ構造

はじめに

　この記事は、『データ構造とアルゴリズム』という本で紹介されているアルゴリズムをPythonで実装したものであり、情報系の勉強をされている方にとってはかなり基本的な内容にとなっています。発展的な内容を学びたい方は、下の目次を見た上でcommand+[を押していただくことを推奨します。

目次

1. 集合の表現
2. 優先度付き待ち行列（ヒープ）
3. ２分探索木
4. AVL木
5. ２-３木
6. ハッシュ
7. ソート
8. バブルソート
9. クイックソート
10. マージソート
11. ヒープソート
12. バケットソート（ビンソート）
13. 基数ソート
14. 有向グラフ
15. ダイクストラのアルゴリズム
16. フロイドのアルゴリズム
17. 深さ優先探索と幅優先探索
18. 一列化
19. 強連結成分
20. 無向グラフ
21. プリムのアルゴリズム
22. クラスカルのアルゴリズム
23. 関節点
24. 文字列の検索
25. 単純な探索
26. KMPアルゴリズム
27. BMアルゴリズム
28. トライ木

実装

　では、Pythonで書いたコードを紹介しながら、それぞれのアルゴリズムを非常に簡単に説明する。理論的な説明をかなり省いたので、詳しい説明は『データ構造とアルゴリズム』参照してください。なお、必要なモジュールは以下の通りです。

import numpy as np
import math
import copy
n = 30

1. 集合の表現

優先度付き待ち行列（ヒープ）

　優先度付き待ち行列とは、「要素に優先度（今回は、値が小さい）を付けておき、その優先度の高いものから順に取り出される」という性質を持ったデータ構造のことである。この性質を単純に実現すると、データの追加のたびに$O(n)$の計算量がかかってしまう。
　そこで、半順序のついた２分木を用いることで、データの追加・取り出しをともに$O(\log n)$で済ませることが可能になる。半順序のついた２分木の持つ性質は以下の通りである。

• ２分木：親ノードは最後尾のものを除いて必ず２つの子ノードを持つ。
• 半順序：親ノードの値は子ノードの値よりも小さい（優先度が大きい）が、兄弟ノードには特別な関係は存在しない。

　こうすることで、

• データの追加時：最後尾にデータを追加して、親との間に逆転がなくなるまで交換を繰り返す。
• データの取出時：根ノードを取り出し、空いた根っこに最後尾のノードを持ってくる。その後、子との間に逆転がなくなるまで交換を繰り返す。

とすれば、計算量は木の高さで抑えられるので、$O(\log n)$で済ませることができる。

#=== swap ===
def swap(arr, i, j):
    tmp = arr[i]
    arr[i] = arr[j]
    arr[j] = tmp

#=== ヒープ(一次元のリストで表現) ===
class heap():
    
    #=== 初期化 ===
    def __init__(self, number_list):
        self.list = []
        for num in number_list:
            self.insert(num)
    
    #=== 挿入 ===
    def insert(self, num):
        self.list.append(num)
        
        # 上へ辿りながら逆転を解消
        index = len(self.list)
        while(index!=1 and self.list[index-1]<self.list[(index//2)-1]):
            swap(self.list, index-1, (index//2)-1)
            index = (index)//2
    
    #=== 最小値を取り出す ===
    def deletemin(self):
        if len(self.list) == 1:
            obj = self.list.pop(0)
            return obj
        obj = self.list[0] # 最小値(先頭)を取り出し、
        self.list[0] = self.list.pop(-1) # 最後尾の値を先頭に持ってくる。
        
        # 下へ辿りながら逆転を解消
        index = 1
        while((len(self.list)>=index*2   and (self.list[index-1] > self.list[index*2-1])) or
               (len(self.list)>=index*2+1 and (self.list[index-1] > self.list[index*2]))):
            # 右側の方が小さい場合は右側とswap(右側の方がindexが大きいので、遅延評価を活かしてこの方法を取る)
            if (len(self.list)>=index*2+1 and self.list[index*2-1] > self.list[index*2]):
                swap(self.list, index-1, index*2)
                index = index*2+1
            else:
                swap(self.list, index-1, index*2-1)
                index = index*2
        return obj
    
    #=== ソート ===
    def sort(self):
        sorted_list = [self.deletemin() for i in range(len(self.list))]
        for num in sorted_list: # 元に戻す。
            self.insert(num)
        return np.array(sorted_list)

sample_heap = heap(np.random.randint(0,100,n))
np.array(sample_heap.list)
>>>array([ 1,  7,  3, 13, 33, 11, 10, 65, 48, 38, 65, 53, 44, 42, 25, 80, 80,
          65, 72, 66, 72, 83, 67, 71, 57, 86, 83, 93, 51, 67])

　なお、上記のコードのように、「配列を用いて表現された半順序のついた２分木」をヒープと呼ぶ。

２分探索木

　ヒープから効率良く取り出すことのできるのは、最小の値のみであった。そこで、任意の値を$O(\log n)$で取り出すことのできるデータ構造を考える。それが、２分探索木である。２分探索木の満たす性質は、以下の通りである。

• 全てのノードは、最大２つまでの子ノードを持つ。
• 左の子孫は全て親ノードよりも小さく、右の子孫は全て親ノードよりも大きい

画像はWikiwandより。（閲覧日：2019/1/9）
　ちなみに、データを取り出した際に空いた穴を埋める際には、

• 子ノードが０：何もしない。
• 子ノードが１：その子を直接持ってくる。
• 子ノードが２：右の子孫で最もあたいの小さい要素を持ってくる。

ことで２分探索木の性質を保つことができる。

class Node():
    def __init__(self, num):
        self.value = num   #ノード自体がもつ数値
        self.left  = None  #左ノード
        self.right = None  #右ノード

#=== 二分探索木 (Binary Search Tree) ===
class BST():
    
    #=== 初期化 ===    
    def __init__(self, number_list):
        self.root = None
        for num in number_list:
            self.insert(num)
    
    #=== 挿入 ===
    def insert(self, num):
        node = self.root
        if node == None:
            self.root = Node(num)
            return
        else:
            while True:
                value = node.value
                if num < value:
                    if node.left == None: 
                        node.left = Node(num)
                        return
                    node = node.left
                else:
                    if node.right == None:
                        node.right = Node(num)
                        return
                    node = node.right
    
    #=== 探索 ===
    def search(self, num):
        node = self.root
        if node == None:
            print("BST is not created.")
            return
        else:
            while True:
                value = node.value
                if num < value:
                    if node.left == None:
                        print("{} is not found.".format(num))
                        return
                    node = node.left
                elif num > value:
                    if node.right == None:
                        print("{} is not found.".format(num))
                        return
                    node = node.right
                else:
                    print("{} is found.".format(num))
                    return                        
    
    # 最小値を取り出す。
    def eject_min(self):
        node = self.root
        if node == None:
            print("BST is not created.")
            return
        else:
            if node.left == None:
                tmp = node.value
                self.root = self.root.right
                return tmp
            else:
                last = None
                while(True):
                    if node.left != None: # 左側（より小さいノード）があるならば、探索を続ける。
                        last = node
                        node = node.left
                    else:
                        tmp = node.value
                        if node.right == None:
                            last.left = None
                        else:
                            last.left = last.left.right
                        return tmp
    
    # 再帰的に関数を呼び出して、小さいものから順に取り出す。
    def sort(self, node, lst):
        if node != None:
            self.sort(node.left, lst)
            lst.append(node.value)
            self.sort(node.right, lst)

sample_bst = BST(np.random.randint(0,100,n))
sort_list = []
sample_bst.sort(sample_bst.root, sort_list)
np.array(sort_list)
>>>array([ 3,  6,  8,  8, 14, 16, 23, 26, 29, 31, 34, 35, 37, 38, 48, 48, 55,
          58, 62, 70, 72, 73, 74, 79, 81, 85, 87, 88, 90, 94])

AVL木

　AVL木は、上記の２分探索木を拡張して、最悪時の計算量も $O(\log n)$ に抑えたものである。（計算量は木の高さに依存するが、通常の２分探索木は木のバランスを保証していないため、ひたすら一方に偏った形の場合、計算量は$O(n)$となってしまう。それでも平均すると$O(\log n)$で抑えることができるが、その証明は省く。）

拡張する内容としては、「どのノードの左右部分木の高さの差も１以下」というもので、この条件が壊れた場合には、回転という操作を行うことで条件を満たす。ここではこの程度の紹介にとどめておく。
画像はWikipediaより。（閲覧日：2019/1/9）

２-３木

　２-３木は、AVL木と同様に平衡木（木の構造が変わるたびにバランスをとるよう操作を行い、最悪の計算量を抑える木構造）の一種である。２−３木の特徴は、「要素は全て葉に格納され、途中のノードは全てインデックスとしてのみ機能する」という点である。なお、インデックスノードは必ず２つまたは３つの子ノードを持ち、インデックス情報として２番目の子の子孫と３番目の子の子孫の最小値を持つ。
画像はWikipediaより。（閲覧日：2019/1/9）

ハッシュ

　ハッシュは、これまでと異なり、順序関係を利用することなく、データの参照、追加、削除をハッシュ値の計算コストのみで実現するデータ構造のことである。データにハッシュ関数という関数をかけることによって値（ハッシュ値）を求め、その値によって一意の場所にデータを格納する、という方法でこれを実現する。
　しかし、現実的にはデータごとに一意のハッシュ値を返すハッシュ関数を求めることは困難（そもそも格納場所には限りがあるので同じ場所に格納されるデータが出てくる。）であり、既にデータが格納されている場所にデータを格納する（衝突）際にどう対処するかによって２種類の方法がある。

・開番地法

　衝突が起きたら、再ハッシュを行うことで別の格納場所に移動する、という手法である。なお、すぐ次の格納場所に移動する再ハッシュの方法を一次ハッシュと呼ぶ。
　なお、データを削除した際には単に空にするとうまくデータを探索できない可能性が出てくる。そこで、deleteというフラグを持つことで、

• 参照の際にdeleteに当たった場合には衝突があったものとして再ハッシュを行う。
• 追加の際にdeleteに当たった場合には単に空だと見なしてデータを格納する。

・チェイン法

　同じ格納場所にデータを複数格納する、という非常に単純な手法である。コードは以下の通り。

# チェイン法（ハッシュは、1の位を採用）
class Hash():
       
    def __init__(self, number_list):
        self.list = [[] for i in range(10)]
        for num in number_list:
            self.insert(num)
    
    def insert(self, num):
        self.list[int(str(num)[-1])].append(num)
        
    def search(self, num):
        if [n for n in self.list[int(str(num)[-1])] if n==num]:
            print("{} is found.".format(num))
        else:
            print("not found.")
    
    def delete(self, num):
        self.list[int(str(num)[-1])].remove(num)

sample_hash = Hash(np.random.randint(0,100,n))
sample_hash.list
>>>[[80, 0],
   [1],
   [42, 82, 52],
   [3, 33, 83, 23, 3, 93],
   [34, 44, 94],
   [15, 35, 45, 35],
   [86, 86, 26],
   [47],
   [48, 98, 28, 48, 18],
   [9, 49]]

2. ソート

バブルソート

　列の最後尾から順に要素を見ていき、後ろの要素の方が前の要素より小さければ交換するという操作を繰り返すソートの方法である。$O(n^2)$の計算量がかかるが、これを改良したものに、シェーカーソート、コームソートなどがある。
バブルソートのコードは以下の通り。

def Bubble_sort(arr):
    for i in range(len(arr)):
        for j in reversed(range(i+1, len(arr))):
            if (arr[j-1] > arr[j]):
                swap(arr,j,j-1)
    return arr

sample_array = np.random.randint(0,100,n)
Bubble_sort(sample_array)
>>>array([ 4,  4,  6,  7, 10, 14, 16, 17, 24, 29, 31, 31, 34, 38, 41, 45, 56,
          58, 62, 64, 64, 68, 73, 76, 85, 91, 91, 94, 97, 99])

クイックソート

　クイックソートは、与えられた配列をある値(pivot)より大きいものと小さいものに分け、それを再帰的に解いた結果をつなぎ合わせることで全体の並べ替えを行う手法のことである。$O(n\log n)$でソートを行うことができる。

def Quick_sort(arr):
    if (len(arr) == 1):
        return arr
    else:
        n1 = arr[0]
        arr_ = arr[arr != n1]
        if (len(arr_) == 0):
            return arr
        else:        
            pivot = n1 if n1>arr_[0] else arr_[0]
            left  = Quick_sort(arr[arr< pivot])
            right = Quick_sort(arr[arr>=pivot])
            return np.r_[left,right]

sample_array = np.random.randint(0,100,n)
Quick_sort(sample_array)
>>>array([ 0,  4,  8, 17, 17, 21, 26, 30, 33, 42, 44, 45, 49, 52, 56, 57, 60,
          62, 63, 64, 66, 71, 76, 79, 87, 89, 90, 93, 95, 98])

ちなみに、小さい方からk番目の要素を取り出したい時には、pivotで分割された片方だけを考えれば良いので、効率が良い。（クイックセレクトと呼ばれる。）

マージソート

　マージソートは、ソート済みの２つの配列をソートして１つの配列にする操作を繰り返すことで全体の並べ替えを行う。$O(n\log n)$でソートを行うことができる。

def Merge_sort(arr):
    length = len(arr)
    if (length == 1):
        return arr
    else:
        left  = Merge_sort(arr[:length//2])
        right = Merge_sort(arr[length//2:])
        return np.array(Merge(left, right))

def Merge(arr1, arr2):
    lst = []
    while(True):
        len1 = len(arr1)
        len2 = len(arr2)
        if (len1==0 and len2==0):
            return lst
        elif (len1==0): 
            lst.append(arr2[0])
            arr2 = arr2[1:]
        elif (len2==0):
            lst.append(arr1[0])
            arr1 = arr1[1:]
        elif (arr1[0] < arr2[0]):
            lst.append(arr1[0])
            arr1 = arr1[1:]
        else:
            lst.append(arr2[0])
            arr2 = arr2[1:]

sample_array = np.random.randint(0,100,n)
Merge_sort(sample_array)
>>>array([ 4,  4,  4,  6, 14, 15, 20, 21, 23, 25, 29, 34, 40, 42, 44, 44, 44,
          46, 48, 50, 51, 57, 59, 64, 69, 82, 83, 94, 96, 98])

ヒープソート

　上で紹介したヒープにデータを全て挿入し、最小値を順に取り出すことでソートを行う。これもk番目までの要素を取り出す時の計算量が抑えられるという特徴がある。$O(n\log n)$でソートを行うことができる。

sample_array = np.random.randint(0,100,n)
sample_heap = heap(sample_array)
sample_heap.sort()
>>>array([16, 17, 20, 21, 26, 26, 30, 33, 35, 38, 42, 46, 46, 48, 51, 58, 60,
          65, 66, 69, 71, 71, 74, 76, 77, 79, 82, 87, 92, 93])

バケットソート（ビンソート）

　データの取り得る範囲が有限個（m個）に限られている場合に利用することができる方法で、あらかじめm個のバケットを用意しておく。そこへ要素を順次挿入していき、最後にバケットを走査しながらデータを集めることでソートが完了する。$O(m+n)$でソートを行うことができる。

def Bucket_sort(arr):
    lst = []
    keys   = [i for i in range(N)]
    values = [0 for i in range(N)]
    bucket = dict(zip(keys, values))
    for e in arr:
        bucket[e] += 1
    for e,n in bucket.items():
        for i in range(n):
            lst.append(e)
    return np.array(lst)

sample_array = np.random.randint(0,100,n)
Bucket_sort(sample_array)
>>>array([ 0,  2,  7, 13, 13, 16, 18, 24, 24, 30, 37, 41, 47, 52, 53, 53, 56,
          58, 62, 63, 68, 72, 76, 79, 81, 90, 90, 91, 92, 96])

基数ソート

　要素の取り得る値が大きい時に上のバケットソートを使うのは非効率である。そこで、各桁に対してバケットソートを行うことで全体のソートを行う。k桁ある場合、$O(kn)$でソートを行うことができる。

def Base_sort(arr,k):
    form = "{:0%d}" % k
    arr_str = [form.format(i) for i in arr]
    for l in range(k):
        tmp = [[] for i in range(10)] 
        for e in arr_str:
            tmp[int(e[k-l-1])].append(e)
        arr_str = [e for inner in tmp for e in inner]
    return np.array([int(e) for e in arr_str])

sample_array = np.random.randint(0,100,n)
Base_sort(sample_array, 2)
>>>array([ 5,  8, 11, 12, 14, 18, 20, 23, 26, 29, 30, 30, 32, 32, 43, 43, 45,
          54, 60, 63, 63, 68, 74, 74, 78, 82, 82, 86, 86, 93])

3. 有向グラフ

　ノード間のエッジに向きが付いているグラフを有向グラフと呼ぶ。

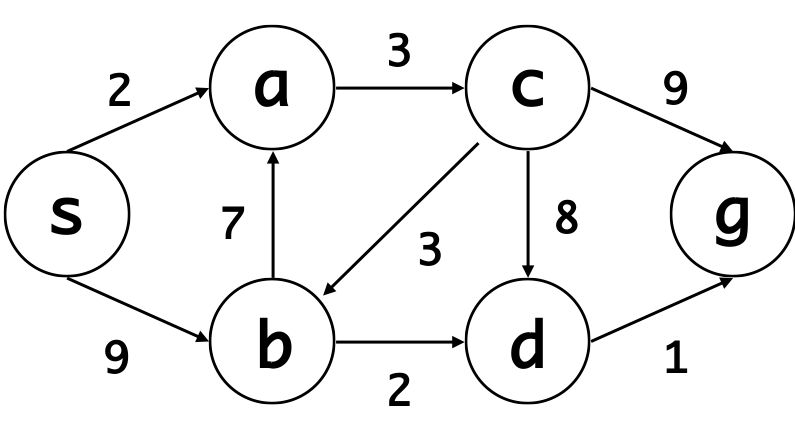
Vertices = ["s","a","b","c","d","g"]
paths = [['s', 'a', 2],
         ['s', 'b', 9],
         ['a', 'c', 3],
         ['b', 'a', 7],
         ['b', 'd', 2],
         ['c', 'b', 3],
         ['c', 'd', 8],
         ['c', 'g', 9],
         ['d', 'g', 1]]
inf = 1000
#=== （有向グラフの）直接移動コスト ===
def d(s, e, paths):
    if s==e: return 0
    return min([path[2] if (path[0] == s and path[1] == e) else inf for path in paths])

ダイクストラのアルゴリズム

　ある出発点から全てのノードまでの最短経路を計算するアルゴリズムである。以下のようにして求める。

1. 出発点からの直接移動コストを記録する。
2. 最もコストの小さいノードを取り上げる。
3. そのノードを経由した方がコストが小さければ、コストを更新する。
4. 以後、2,3の繰り返し。

def Dijkstra(V,paths,start):
    N = len(V)
    costs = [0 for i in range(N)]
    for i,v in enumerate(V):
        costs[i] = d(start, v, paths)
        
    cost_dict  = dict(zip(V,costs)) # それぞれの辺までのコストを格納する方
    cd         = copy.deepcopy(cost_dict) # 残りのノードを参照する方
    cd.pop(start)
    
    for l in range(N-1):
        new_v = min(cd,key=cd.get)
        cd.pop(new_v)
        for v in cd.keys():
            cd[v] = min(cost_dict[v], cost_dict[new_v] + d(new_v,v,paths))
            cost_dict[v] = cd[v]
    return cost_dict

Dijkstra(Vertices, paths, "s")
>>>{'a': 2, 'b': 8, 'c': 5, 'd': 10, 'g': 11, 's': 0}
Dijkstra(Vertices, paths, "a")
>>>{'a': 0, 'b': 6, 'c': 3, 'd': 8, 'g': 9, 's': 1000}

　なお、ダイクストラのアルゴリズムは、コストが非負である時には最適な解を返す。

フロイドのアルゴリズム

　全てのノードから全てのノードへの最短経路を計算するアルゴリズムである。

def Floyd(V,paths,print_):
    N = len(V)
    costs = np.zeros((N,N))
    for i,u in enumerate(V):
        for j,v in enumerate(V):
            costs[i,j] = d(u,v,paths)

    for w in range(N):
        for u in range(N):
            for v in range(N):
                costs[u,v] = min(costs[u,v], costs[u,w]+costs[w,v])
    
    #=== 綺麗に出力する ===
    if print_:
        costs = costs.astype(int)
        str_tmp  = "入\出"
        num_temp = ""
        for i in range(N):
            num_temp += " {"+"0[{}]:4d".format(i)+"} "
            str_tmp += " {"+"0[{}]:>4".format(i)+"} "

        print(str_tmp.format(V))
        for i,u in enumerate(V):
            print("　{}　".format(u),end="")
            print(num_temp.format(costs[i]))
    #====================
    else:
        return costs

Floyd(Vertices, paths, print_=True)
>>>入\出    s     a     b     c     d     g 
　   s　    0     2     8     5    10    11 
　   a　 1000     0     6     3     8     9 
　   b　 1000     7     0    10     2     3 
   　c　 1000    10     3     0     5     6 
   　d　 1000  1000  1000  1000     0     1 
   　g　 1000  1000  1000  1000  1000     0 

Floyd(Vertices, paths, print_=False)
>>>array([[    0.,     2.,     8.,     5.,    10.,    11.],
          [ 1000.,     0.,     6.,     3.,     8.,     9.],
          [ 1000.,     7.,     0.,    10.,     2.,     3.],
          [ 1000.,    10.,     3.,     0.,     5.,     6.],
          [ 1000.,  1000.,  1000.,  1000.,     0.,     1.],
          [ 1000.,  1000.,  1000.,  1000.,  1000.,     0.]])

深さ優先探索と幅優先探索

Vertices = ["a","b","c","d","e","f","g"]
paths = [("a","b"),
         ("a","c"),
         ("b","d"),
         ("b","e"),
         ("c","f"),
         ("c","g"),]

深さ優先探索

　兄弟を探索する前に子・子孫を探索する方法である。

def DepthFirstSearch(V,paths):
    lst = []
    visited = dict([(v,False) for v in V])
    for v in V:
        dfs(v,visited,paths,lst)
    return lst
        
def dfs(v,visited,paths,lst):
    if visited[v]: return
    visited[v] = True
    lst.append(v)
    for v,u in [path for path in paths if path[0] == v]:
        dfs(u,visited,paths,lst)

DepthFirstSearch(Vertices,paths)
>>>['a', 'b', 'd', 'e', 'c', 'f', 'g']

幅優先探索

　子・子孫を探索する前に兄弟を探索する方法である。

def BreadthFirstSearch(V,paths):
    lst = []
    visited = dict([(v,False) for v in V])
    for v in V:
        bfs(v,visited,paths,lst)
    return lst
        
def bfs(s,visited,paths,lst):
    Q = [s]
    while(Q):
        v = Q.pop(0)
        if not visited[v]:
            visited[v] = True
            lst.append(v)
            for v,u in [path for path in paths if path[0] == v]:
                Q.append(u)

BreadthFirstSearch(Vertices,paths)
>>>['a', 'b', 'c', 'd', 'e', 'f', 'g']

一列化

　閉路がないグラフが与えられた時に、順序がエッジの向きに一致するように一列に並べる操作のことである。深さ優先探索の帰りがけにノードを出力することで一列化の逆順が得られるので、これを利用する。

def Topological(V,paths):
    lst = []
    visited = dict([(v,False) for v in V])
    for v in V:
        ts(v,visited,paths,lst)
    return lst[::-1]
    
        
def ts(v,visited,paths,lst):
    if visited[v]: return
    visited[v] = True
    for v,u in [path for path in paths if path[0] == v]:
        ts(u,visited,paths,lst)
    lst.append(v)

Topological(Vertices,paths)
>>>['a', 'c', 'g', 'f', 'b', 'e', 'd']

強連結成分

　有向グラフの部分グラフであって、その中の任意のノード間の行き来が可能であるようなもののうち、できるだけ大きくとったものである。

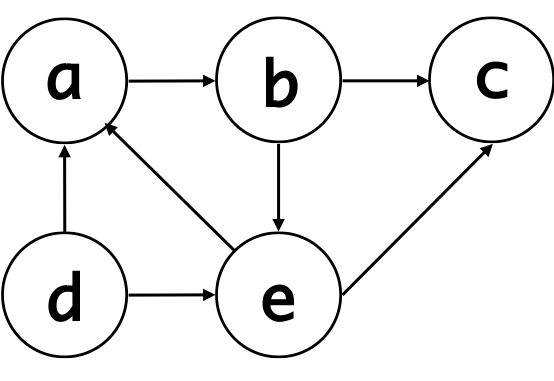
Vertices = ["a","b","c","d","e"]
paths = [("a","b"),
         ("b","c"),
         ("b","e"),
         ("d","a"),
         ("d","e"),
         ("e","a"),
         ("e","c")]

def SCC(V,paths):
    lst = []
    ts  = Topological(V,paths)
    visited = dict([(v,False) for v in V])
    paths_r = [(path[1],path[0]) for path in paths]
    for v in reversed(ts[::-1]):
        dfs(v,visited,paths_r,lst)
        lst.append("/")
    return lst

SCC(Vertices,paths)
>>>['d', '/', 'a', 'e', 'b', '/', '/', '/', 'c', '/']

4. 無向グラフ

　エッジが向きを持たないグラフを無向グラフと呼ぶ。
画像はWikipediaより。（閲覧日：2019/1/9）

Vertices = ["a","b","c","d","e","f","g"]
paths = [['a', 'b', 7],
         ['a', 'd', 5],
         ['b', 'c', 8],
         ['b', 'd', 9],
         ['b', 'e', 7],
         ['c', 'e', 5],
         ['d', 'e', 15],
         ['d', 'f', 6],
         ['e', 'f', 8],
         ['e', 'g', 9],
         ['f', 'g', 11]]

#===（無向グラフの）直接移動コスト===
def d(s, e, paths):
    if s==e: return 0
    return min([path[2] if (s in path and e in path) else inf for path in paths])

プリムのアルゴリズム

　プリムのアルゴリズムと次に紹介するクラスカルのアルゴリズムは、最小木（コスト最小の極大木）を効率的に求めるアルゴリズムである。（極大木とは、任意のノードから任意のノードへの経路が存在する、閉路を含まない部分木のこと）

　プリムのアルゴリズムは、任意のノードからスタートし、周りのエッジのうち最もコストが小さいエッジを加える操作を繰り返すことで最小木を構築するアルゴリズムである。

def Prim(V,paths):
    N = len(V)
    start = V[0] # 任意の点
    costs = [0 for i in range(N)]
    for i,v in enumerate(V):
        costs[i] = d(start,v,paths)
    
    T = []
    Node = dict(zip(V,[start for i in range(N)]))
    
    cost_dict = dict(zip(V,costs))
    cost_dict.pop(start)
    
    for i in range(N-1):
        w = min(cost_dict, key=cost_dict.get)
        cost_dict.pop(w)
        T.append([w,Node[w]])
        for v in cost_dict.keys():
            if d(w,v,paths)<cost_dict[v]:
                cost_dict[v] = d(w,v,paths)
                Node[v]  = w
    return T 

Prim(Vertices,paths)
>>>[['d', 'a'], ['f', 'd'], ['b', 'a'], ['e', 'b'], ['c', 'e'], ['g', 'e']]

クラスカルのアルゴリズム

　クラスカルのアルゴリズムは、ノードを（閉路ができないように）コストが小さい順に加えていくことで最小木を構築するアルゴリズムである。

def Kruskal(V,paths):
    paths = sorted(paths, key=lambda x:x[2]) # 辺のコストが小さい順に並べる。
    U = [[v] for v in V]
    T = []
    while(len(paths)>0):
        min_path = paths.pop(0)
        T_1 = [u for u in U if min_path[0] in u][0]
        T_2 = [u for u in U if min_path[1] in u][0]
        if T_1 != T_2:
            T.append(min_path)
            U.remove(T_1)
            U.remove(T_2)
            U.append(T_1+T_2)
    return T

Kruskal(Vertices,paths)
>>>[['a', 'd', 5],
    ['c', 'e', 5],
    ['d', 'f', 6],
    ['a', 'b', 7],
    ['b', 'e', 7],
    ['e', 'g', 9]]

関節点

関節点とは、その点を除くとグラフが２つ以上のグラフに分断されてしまうようなノードのことである。

• 深さ優先探索を行い、深さ優先極大木を作りながら行きがけ順に番号num[v]を振る。
• 各ノードから深さ優先極大木に沿って0段以上下がった後に、エッジを一度だけ使ってどこまで上に戻れるか」を表した値low[v]を計算する。

　この時、vの子ノードwでlow[w]>=num[v]を満たすものが存在すれば、wからはvより上流に戻る経路が存在しないことを表すので、vが関節点となる。

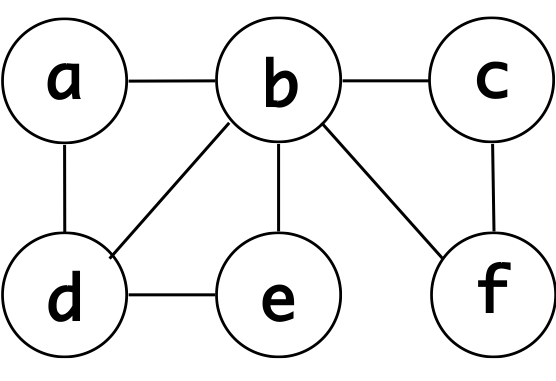
Vertices = ["a","b","c","d","e","f"]
paths = [("a","b"),
         ("a","d"),
         ("b","c"),
         ("b","d"),
         ("b","e"),
         ("b","f"),
         ("c","f"),
         ("d","e")]

def Articulation_point(V,paths):
    visited = dict([(v,False) for v in V])
    num = dict([(v,inf) for v in V])
    low = dict([(v,inf) for v in V])
    for v in V:
        ap(v,visited,paths,num,low)
    return num,low    
        
def ap(v,visited,paths,num,low):
    #=== 前向きフェーズ ===
    global n
    son=inf; back=inf;
    
    if visited[v]: return
    visited[v] = True
    num[v] = n
    n+=1
    for v,u in [[path[0],path[1]] for path in paths if path[0] == v] +\
                   [[path[1],path[0]] for path in paths if path[1] == v]:
        ap(u,visited,paths,num,low)

    #=== 後ろ向きフェーズ ===
    # ①vの子のうち、最も値の小さいlow
    son_low = [low[key] for key,val in num.items() if val>num[v] and val<inf]
    if len(son_low)>0:
        son = min(son_low)
    
    # ②vから出ている後退辺を一度だけ使って移動できる点のうち、最も値の小さいnum
    back_num = [num[path[1]] for path in paths if v == path[0]] + [num[path[0]] for path in paths if v == path[1]]
    if len(back_num)>0:
        back = min(back_num)
    
    low[v] = min(num[v],son,back)

Articulation_point(Vertices,paths)
>>>({'a': 1, 'b': 2, 'c': 3, 'd': 5, 'e': 4},
    {'a': 1, 'b': 1, 'c': 1, 'd': 1, 'e': 1})

　low[c]=2>=num[b]=2より、bが関節点である。

5. 文字列の検索

　文書の中から特定の文字列を見つけ出す方法について考える。

単純な探索

def simple(text,pattern):
    N = len(text)
    M = len(pattern)
    i=0; j=0; # iは文書中の位置、jは検索文字列中の位置
    while(i<=N-M):
        while(j<M and text[i+j]==pattern[j]):
            j += 1
        if j==M: return i
        i+=1
        j=0
    return False

text = "ATGGCTAATTATAAAAGGTATTAAAGTCGCC"
pattern = "TATAAAAG"
simple(text,pattern)
>>>9

KMPアルゴリズム

　例えばabcdという文字列を探していて、4文字目のdで不一致があったとする。その場合、１つ、２つずらしても一致するはずがないことは明らかである。そのため、３つずらして照合を始めた方が効率が良い。これを行うアルゴリズムをKMPアルゴリズムと言う。なお、文書に関係なく検索文字列を調べることで照合中に不一致があった場合に何文字進めれば良いのか計算することができる。

def KMP_skip(pattern):
    M = len(pattern)
    lst = [i+1 if pattern[0]==pattern[i] else i for i in range(M)]
    
    for i in range(1,M):
        for j in reversed(range(i)):
            # i-j-1 ~ i-1 番目までと 0 ~ j 番目までが一致し、i番目とj+1番目が異なるjを探す。
            if (pattern[j] == pattern[i-1]) and (pattern[j+1] != pattern[i]):
                m=j; n=i-1;
                while(m>=0):
                    if pattern[m]==pattern[n]:
                        m-=1; n-=1;
                    else:
                        break
                if m==-1: 
                    lst[i] = i-j-1
                    break
    return lst

p1="abcabd"
KMP_skip(p1)
>>>[1, 1, 2, 4, 4, 3]

p2="aabaab"
KMP_skip(p2)
>>>[1, 2, 1, 4, 5, 4]

def KMP(text,pattern):
    N = len(text)
    M = len(pattern)
    skip = KMP_skip(pattern)
    i=0; j=0;
    while(i<=N-M):
        while(j<M and text[i+j]==pattern[j]):
            j += 1
        if j==M: return i
        i+=skip[j]
        j=max(0,j-skip[j])
    return False

text = "ATGGCTAATTATAAAAGGTATTAAAGTCGCC"
pattern = "TATAAAAG"
KMP(text,pattern)
>>>9

BMアルゴリズム

　上２つと異なり、検索文字列の照合を後ろから行う。こうすることで、例えばabcdという文字列を探していて、dに対応する文字がeだったとすると、一気に４文字分ずらすことが可能になる。これを行うアルゴリズムをBMアルゴリズムと言う。

def BM_skip(pattern):
    M = len(pattern)
    lst = []
    for i in range(M):
        lst.append((pattern[i],M-i-1))
    return dict(lst)

p1="abcabd"
BM_skip(p1)
>>>{'a': 2, 'b': 1, 'c': 3, 'd': 0}

p2="aabaab"
BM_skip(p2)
>>>{'a': 1, 'b': 0}

def BM(text,pattern):
    N = len(text)
    M = len(pattern)
    skip = BM_skip(pattern)
    i=0;
    while(i<=N-M):
        j = M-1
        while(j>=0 and text[i+j]==pattern[j]):
            j -= 1
        if j==-1: return i
        i += max(1, skip[text[i+j]]+j-M+1)
    return False

text = "ATGGCTAATTATAAAAGGTATTAAAGTCGCC"
pattern = "TATAAAAG"
BM(text,pattern)
>>>9

トライ木

　文字列の検索に適したデータ構造として、木構造を用いるものがある。各ノードが１文字だけをもった木構造であるトライ木や、トライ木の欠点であるメモリ消費を抑える３分探索木、パトリシア木(基数木)などが知られている。
画像はWikipediaより。（閲覧日：2019/1/9）

参考

五十嵐健夫（2017）『データ構造とアルゴリズム』（第５刷）数理工学社