はじめに
本記事は、話題のニュースを分析シリーズ第2弾となります(第1弾はこちら)
以下にご留意頂ければと思います。
・ゴシップなテーマではありますが、内容は技術の共有を目的としているため、個人名・企業名等は伏せさせて頂きます
・本記事の内容は、自由に転載頂いて構いません
・本記事に対する問い合わせは、私のTwitterまでお願い致します
また、文中のコードはGitHubリポジトリにもアップロードしております
動機
2021年夏は、インフルエンサーの炎上が続発し、社会的に大きく取り上げられることとなりました。
炎上するとYouTubeに他のユーザーからの批判的な動画が多くアップロードされることとなるのですが、これらの動画をよく見ると、アップロードしたユーザーの登録者数や再生回数が大きく伸びているケースが多いと感じました。

そこで今回、炎上がYouTubeの視聴者行動にどのような影響を与えるのかを、統計的に分析してみました。
分析内容
ご存知の方も多いかと思いますが、2021年8月にエンジニア業界では有名なインフルエンサー(以下、単に**「インフルエンサー」と呼ばせて頂きます)が、とあるリーク記事をきっかけにいわゆる炎上状態に陥り、YouTubeに関連動画が大量アップ(アップロードした炎上参加ユーザは以後「批評者」**と呼ばせて頂きます)される事態となりました。
詳細内容についてはQiita規約から外れるため触れませんが、きっかけとなったリーク情報は8/9に公開されているため、この日を境にインフルエンサー&批評者の再生回数・チャンネル登録者数がどのように変化したかを、時系列分析の手法で分析してみました
注意点
・本記事を書くにあたり、私個人としてはインフルエンサー側、批評者側どちらでもない中立的な立場での執筆を心がけたいと思います
・私はマーケティング分析の専門家ではないので、今回の分析手法(ARIMAモデル)は工業的なバックグラウンドに基づいたものとなります。よりマッチした手法をご存知であれば、コメント欄でご指摘頂けるとありがたいです
対象とするYouTubeチャンネルの選定
以下のYouTubeチャンネルを分析対象として選定しました。
| No. | 分類 | 内容 | 選定方法 | チャンネル数 |
|---|---|---|---|---|
| 1 | influencer_main | 分析内容で言及したインフルエンサー | - | 1 |
| 2 | criticizer | 上記インフルエンサーの関係(主に批判的な)動画をアップロードしたYouTuber | YouTube検索でインフルエンサー名で検索し、筆者が目視で動画確認 | 14 |
| 3 | business | 上記以外のビジネス系YouTuber | こちらのサイトで、直近3ヵ月の動画投稿ペースが落ちていないYouTuberを無作為に選定 | 20 |
| 4 | influencer_other | メイン以外の炎上インフルエンサー(ビジネス系) | 直近1年以内に炎上を経験したビジネス系YouTuber | 4 |
| 5 | influencer_drunk | メイン以外の炎上インフルエンサー(ビジネス系以外) | 2021年6月に同一の不祥事で週刊誌報道されたYouTuber | 19 |
| ※3は、再生回数や登録者数の変化が炎上に関係するものなのか、ビジネス系YouTuber全体の傾向なのかを切り分けるための比較用に取得します | ||||
| ※4, 5は、炎上したチャンネルの変化が普遍的なものなのかを判断するためのN増し用に取得します | ||||
| ※どの分類も、十分なN数を稼ぐため登録者数10000人以上のチャンネルのみを抽出しています |
上記をふまえて、以下のように分析対象チャンネルを一覧でまとめたchannel_ids.csvを作成しました。

データの取得
本章は分析結果と直結しないデータ取得部の解説となるため、結果だけ見たい方は分析まで飛んでください。
分析対象のYouTubeチャンネルごとに、分析に使用するデータを取得します。
YouTubeからのデータ取得方法には主に以下の2種類の方法があるので、両者を解説します。
実際に使用したのは2のみなので、基本的には2の方法だけ見て頂ければ十分かと思います
- YouTube APIを使用する方法(現在のデータを取得)
- Noxinfluencerにアクセスする方法(過去のデータを取得)
1. YouTube APIでデータ取得(今回は不使用)
PythonとYouTube Data APIを使用して、YouTubeの各種データを取得します。
本手法は現在のデータしか取得することができないので、
今回のように過去の推移データを取得したい場合は、定期実行してデータを貯める必要があります。
すなわち今回の分析では本手法は使用しません。
**「使用しないツールを学ぶのは生産性が低い!」と感じた方は、今回実際に使用したNoxinfluenceを使用する方法**まで飛んで頂ければと思います。
以下の手順で進めます
YouTube Data APIの登録
PythonからYouTube情報を取得するために必要な、YouTube Data API(Googleのサービス)に登録します。
・Google Cloud PlatFormにログイン(アカウントがなければ登録してください)し、「ホーム」→「ダッシュボード」の順でクリックします
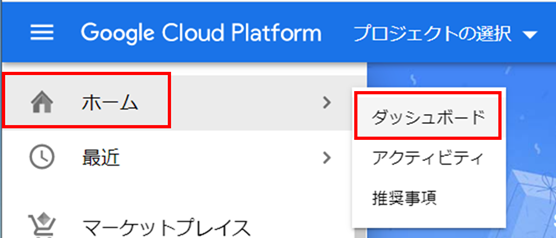
・プロジェクト名と場所を記載します(個人開発なら場所は「組織なし」でよいかと思います)

・プロジェクトに入り、「APIとサービス」→「ライブラリ」をクリックします**
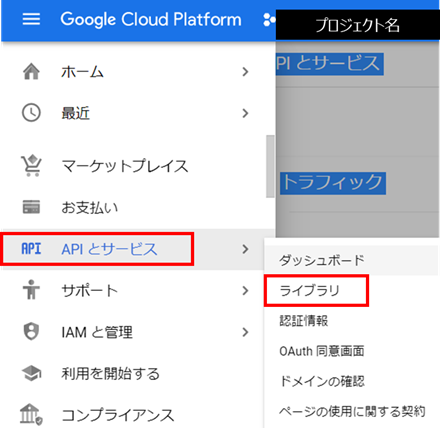
・「youtube data api v3」で検索し、出てきた候補をクリックします
・「認証情報」→「認証情報を作成」→「APIキー」と進み、APIキーを作成します
Google API Clientのインストール
YouTube等の情報を取得するPythonのライブラリ、Google API Clientを下記コマンドでインストールします
pip install google-api-python-client
データ取得コードの実装
以下の手順で、データ取得コードを実装します(こちらの記事を参考にさせて頂きました)
A. YoutubeチャンネルIDから、チャンネル統計情報を取得
B. チャンネル統計情報から必要な情報のみ抜き出し
C. 上記処理をループ処理で一括実行してCSV保存
A.YoutubeチャンネルIDからチャンネル統計情報を取得
Channels: list APIを使用して、チャンネルIDからチャンネルの統計情報を取得します
入力値となるチャンネルIDは、以下のようにチャンネルのURLから取得できます。
https://www.youtube.com/channel/[チャンネルID]
以下のようなメソッドで、チャンネル統計情報を取得します
from googleapiclient.discovery import build
API_SERVICE_NAME = "youtube"
API_VERSION = "v3"
def get_channel_detail(channel_id, api_key):
"""チャンネルIDからチャンネル詳細情報を取得"""
youtube = build(API_SERVICE_NAME, API_VERSION, developerKey=api_key)
search_response = youtube.channels().list(
part='snippet,statistics',
id=channel_id,
).execute()
print(f'Channel_name={search_response["items"][0]["snippet"]["title"]}')
return search_response['items'][0]
取得した戻り値の中身は、以下のようになります。
'statistics'の中に、お目当ての再生回数やチャンネル登録者数が含まれています
{'kind': 'youtube#channel',
'etag': 'リソースの競合を防ぐためのタグ※',
'id': 'チャンネルID',
'snippet': {'title': 'チャンネルタイトル',
'description': 'チャンネル概要文',
'publishedAt': '登録日',
'thumbnails': {サムネイル画像のURL等},
'localized': {'title': 'チャンネルタイトル',
'description': 'チャンネル概要文'},
'country': '国名'},
'statistics': {'viewCount': '総再生回数',
'subscriberCount': 'チャンネル登録者数',
'hiddenSubscriberCount': '登録者数表示の有無',
'videoCount': '動画数'}}
※etagの詳細はこちらを参照ください
B. チャンネル統計情報から必要な情報のみ抜き出し
Aで取得したデータの中から、再生数や登録者数等の必要情報のみを抜き出します(日時はdatetime型に変更)
from googleapiclient.discovery import build
from datetime import datetime
def get_date(str_date):
"""日時文字列をdatetimeに変換(フォーマットが動画により変わるので注意)"""
date_list = str_date.replace('Z','').split('T')
year, month, date = date_list[0].split('-')
hour, minute, sec = date_list[1].split(':')
sec = sec.split('.')[0]
return datetime(int(year),int(month),int(date),int(hour),int(minute),int(sec))
def get_subscriber_viewcount(channel_id, api_key):
"""チャンネルIDから動画の総再生数とチャンネル登録者数を取得"""
# 取得した情報の保持用dict
subscriber_viewer_dict = {}
subscriber_viewer_dict['api_date'] = datetime.today() # 取得日
subscriber_viewer_dict['channel_id'] = channel_id # チャンネルID
# チャンネルIDからチャンネル情報を取得
channel_detail = get_channel_detail(channel_id, api_key)
subscriber_viewer_dict['channel_name'] = channel_detail['snippet']['title'] # チャンネル名
subscriber_viewer_dict['channel_publish_date'] = get_date(channel_detail['snippet']['publishedAt']) # チャンネル作成日
subscriber_viewer_dict['subscriber_count'] = int(channel_detail['statistics']['subscriberCount']) # 登録者数
subscriber_viewer_dict['total_view_count'] = int(channel_detail['statistics']['viewCount']) # 動画総再生数
subscriber_viewer_dict['video_count'] = int(channel_detail['statistics']['videoCount']) # 動画数
print(f'video count = {subscriber_viewer_dict["video_count"]}')
return subscriber_viewer_dict
C. 上記処理をループ処理で一括実行してCSV保存
A, Bの処理を1回ずつ実行すると手間が掛かるので、チャンネルIDをlistで保持しておき、一括実行してCSV形式で保存します。
import pandas as pd
import os
import csv
API_KEY = '前節で取得したAPIキー'
CHANNEL_IDS = [チャンネルIDのリスト]
CSV_PATH = 'CSV出力先のパス'
# チャンネル登録者数・再生数を取得
start_date = datetime.today()
channel_info_list = []
for i, channel_id in enumerate(CHANNEL_IDS):
# チャンネルIDからチャンネル情報
print(f'Channnel No.{i} start')
subscriber_and_viewer_dict = get_subscriber_viewcount(channel_id, API_KEY)
channel_info_list.append(subscriber_and_viewer_dict)
df_channel_info = pd.DataFrame(channel_info_list)
df_channel_info['start_date'] = start_date
df_channel_info['end_date'] = datetime.today()
# CSV出力(追記する場合の処理も記載)
# 出力ファイル存在しないとき、新たに作成
if not os.path.exists(CSV_PATH):
df_channel_info.to_csv(CSV_PATH, encoding='utf_8_sig', index=False)
# 出力ファイル存在するとき、1行ずつ追加
else:
with open(CSV_PATH, 'a', encoding='utf_8_sig', newline='') as f:
for _, row in df_channel_info.iterrows():
writer = csv.DictWriter(f, row.to_dict().keys())
writer.writerow(row.to_dict())
実行すると、以下のようなCSVファイルが出力されます(直接のチャンネル情報は隠してあります)
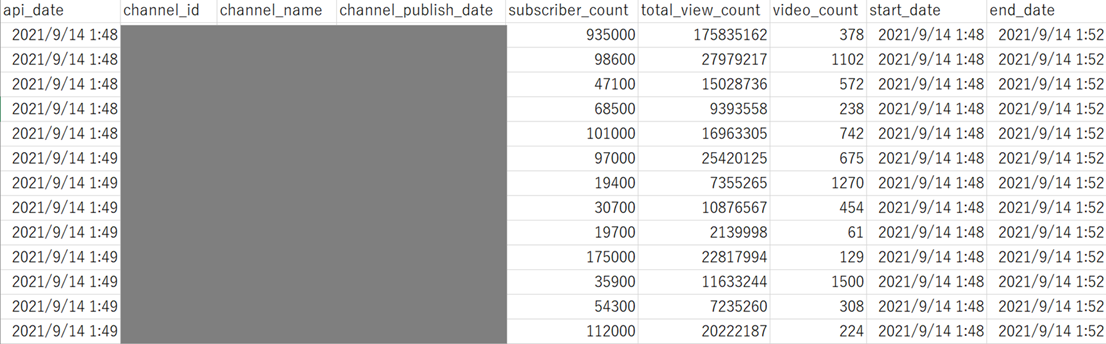
2. NoxInfluencerにアクセスしてデータ取得(過去のデータを取得)
**Noxinfluencer**とは、YouTube分析関係のサービスを提供するWebツールです(基本的に無料ですが、一部サービスのみ有料)
NoxInfluencerは独自にYouTubeの情報を蓄積しているため、過去のデータを取得することができます(具体的な回数は分かりませんが、リクエスト数に上限があるようなので使い過ぎに注意してください)
YouTube APIでは過去のデータを取得できないので、今回はこちらを利用して、対象チャンネルの過去データを取得します。
以下の手順で進めます
A. 該当チャンネルの分析ダッシュボードにアクセス
B. ダッシュボードの情報を取得するAPIの探索
C. APIからデータ取得するPythonコードの作成
A. 該当チャンネルの分析ダッシュボードにアクセス
**Noxinfluencer**のトップページにアクセスし、チャンネル名で検索して分析ダッシュボードに移動します

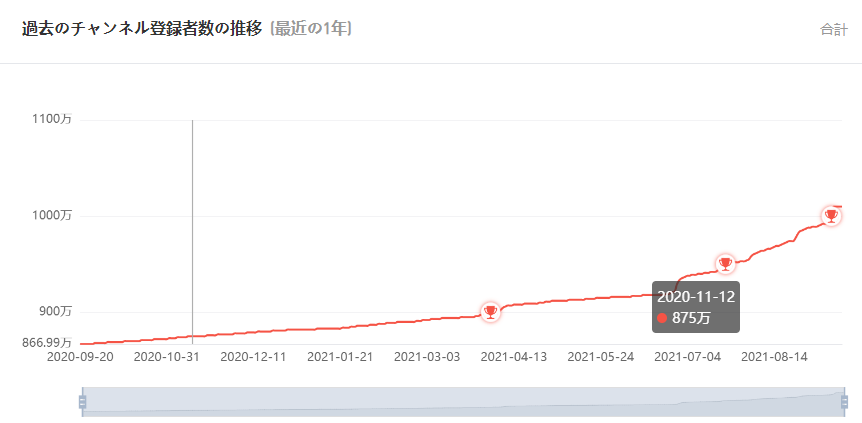
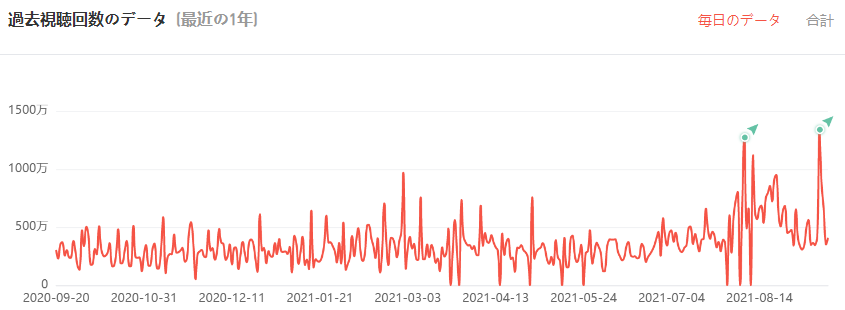
取得したいデータのグラフ確認
取得したいデータが表示されているグラフを確認します。
今回は、以下の2グラフ(例に挙げた図はHikakinさんのグラフです、ご存知だとは思いますが炎上とは無関係です)を取得します。
B. グラフのデータを取得するAPIのURLを特定
移動した分析ダッシュボード上で右クリックし、「検証」を押します
開発者ツールが開くので、「Network」タブをクリックし、記録ボタン(赤丸)を押してF5で画面更新します
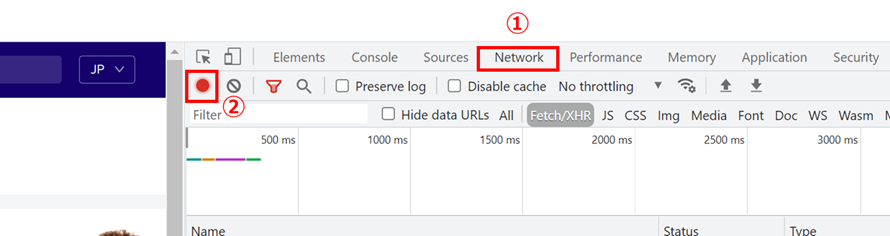
大量のファイルが表示されるので、「Fetch/XHR」ボタンを押してフィルタリングします
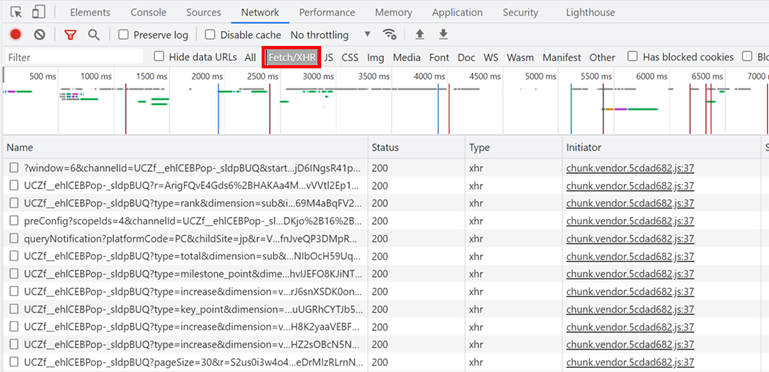
どれかのファイルを選択して「Response」タブを押した後にファイルを1つずつ確認し、グラフとResponse内容が一致するファイルを探します
(割と骨が折れます…)
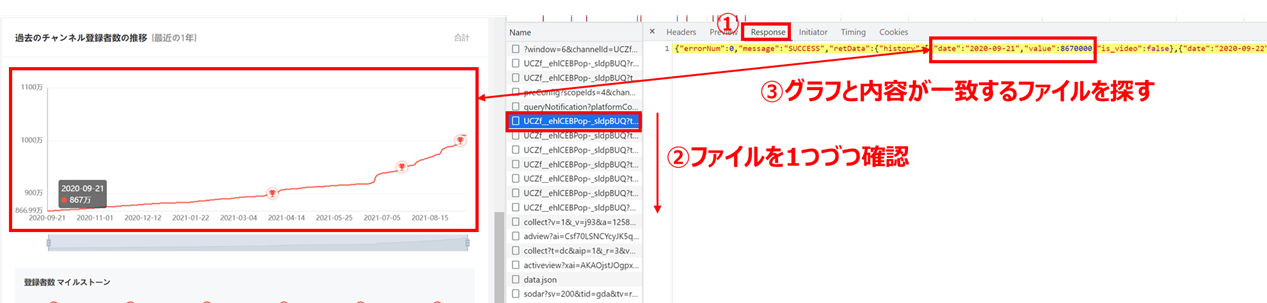
「Headers」タブを押して表示されるURLをコピペします
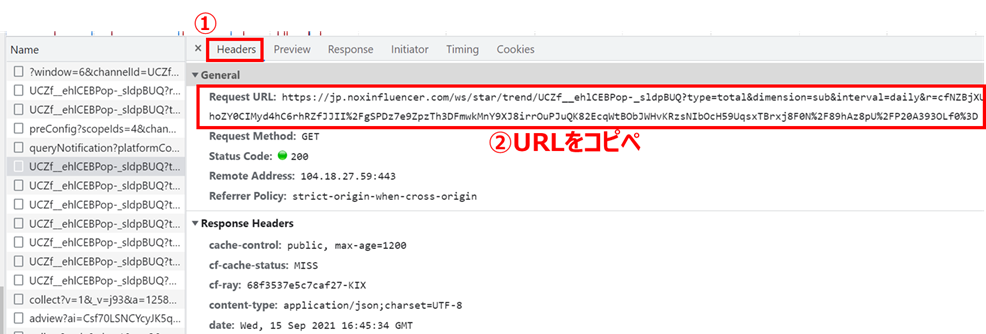
同じ操作を、「①過去のチャンネル登録者数の推移」、「②過去再生回数のデータ」両者に対して実施し、それぞれAPIのURLをメモします。
C. APIからデータ取得するPythonコードの作成
BでメモしたAPIを使用し、過去のチャンネル登録者数、再生回数のデータを取得してCSV出力するコードを作成します。
APIのURLは時間経過で無効となってしまうのでループ実行できず、チャンネルごとに個々で実行する必要があり手間が掛かりますが、頑張ってください(笑)
import requests
import json
import pandas as pd
import csv
import os
from datetime import datetime
CSV_PATH = 'CSV出力先'
URL_SUBSCRIBERS = '①過去のチャンネル登録者数の推移を取得するAPIのURL'
URL_VIEWCOUNT = '②過去の再生回数の推移を取得するAPIのURL'
# 登録者数の履歴を取得
def get_subscribers_history(url_subscribers):
response = requests.get(url_subscribers)
response_dict = json.loads(response.text)
df_response = pd.DataFrame(response_dict['retData']['history'])
df_response['date'] = pd.to_datetime(df_response['date']) # date列をdatetime型に変換
df_response = df_response.rename(columns={'value': 'subscriber_count'}) # 列名変更
return df_response
# 再生回数の履歴を取得
def get_viewcount_history(url_viewcount):
response = requests.get(url_viewcount)
response_dict = json.loads(response.text)
df_response = pd.DataFrame(response_dict['retData']['history'])
df_response['date'] = pd.to_datetime(df_response['date']) # date列をdatetime型に変換
df_response = df_response.rename(columns={'value': 'view_count'}) # 列名変更
return df_response
# データを取得してPandasのDataFrameに格納してマージ
df_subscribers = get_subscribers_history(URL_SUBSCRIBERS)
df_viewcount = get_viewcount_history(URL_VIEWCOUNT)
df_history = pd.merge(df_subscribers, df_viewcount[['date', 'view_count']], how='left', on='date')
# URLから抜き出したチャンネルIDからチャンネル名を取得
channel_id = URL_SUBSCRIBERS.split('trend/')[1].split('?')
df_history['channel_name'] = get_channel_detail(channel_id, API_KEY)['snippet']['title']
df_history['acquisition_date'] = datetime.today()
# CSV出力(追記する場合の処理も記載)
# 出力ファイル存在しないとき、新たに作成
if not os.path.exists(CSV_PATH):
df_history.to_csv(CSV_PATH, encoding='utf_8_sig', index=False)
# 出力ファイル存在するとき、1行ずつ追加
else:
with open(CSV_PATH, 'a', encoding='utf_8_sig', newline='') as f:
for _, row in df_history.iterrows():
writer = csv.DictWriter(f, row.to_dict().keys())
writer.writerow(row.to_dict())
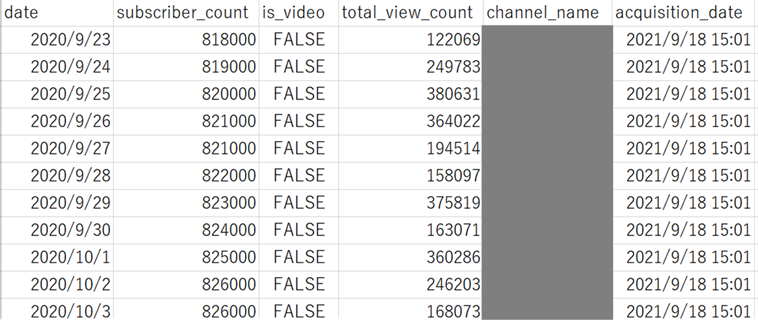
実行すると、以下のようなCSVファイルが出力されます(チャンネル名は隠してあります)
分析
インフルエンサー側、批評者側それぞれのチャンネル登録者数・再生回数が炎上を境にどのように変化したかを、時系列分析の手法で分析していきます
かなり長いので、結論だけ見たい方はまとめまで飛んでください。
批評者側の分析
炎上を境に、批評者のチャンネル登録者数および再生回数が増えたかを分析します。
データの選定方法は以下となります
・炎上日以降にインフルエンサー関係の動画を2動画以上アップロードしたチャンネルを選定
・炎上後40日間のデータを「炎上後データ」、そのおよそ倍の炎上前84日間(12週間≒3ヵ月)のデータを「炎上前データ」(および時系列分析の学習用データ)として使用
可視化とデータクレンジング
まずはデータを可視化し、必要に応じて異常値の補完を行います。
以下のスクリプトでPandasのDataFrameにデータを読み込みます。
import pandas as pd
# 各種定数の指定
NOX_CSV_PATH = 'NoxInfluencer取得データの格納パス'
AFTER_FLAMING = 40 # 炎上後の分析対象日数
BEFORE_FLAMING = 84 # 炎上前の分析対象日数
# データの読込
df_channels = pd.read_csv('./channel_ids.csv', encoding='utf_8_sig', parse_dates=['flaming_date'])
df_noxinfluencer = pd.read_csv(NOX_CSV_PATH, encoding='utf_8_sig', parse_dates=['date', 'acquisition_date'])
# 読み込んだデータを結合
df = pd.merge(df_noxinfluencer, df_channels, how='left', left_on='channel_name', right_on='name').drop(columns=['name'])
# 2動画以上アップロードした批評者チャンネルに絞る
df_criticizer = df[(df['classification']=='criticizer')
& (df['critcizing_videos'] >= 2)].copy()
print(df_criticizer.shape)
df_criticizer.head()
(2686, 11)
date subscriber_count is_video view_count channel_name acquisition_date channel_id classification transferred_name critcizing_videos flaming_date
360 2020-09-23 49000 False 7861.0 **** 2021-09-18 15:02:56.725555 **** criticizer A 37.0 NaT
361 2020-09-24 49000 False 16826.0 **** 2021-09-18 15:02:56.725555 **** criticizer A 37.0 NaT
362 2020-09-25 49000 False 6299.0 **** 2021-09-18 15:02:56.725555 **** criticizer A 37.0 NaT
363 2020-09-26 49100 False 6299.0 **** 2021-09-18 15:02:56.725555 **** criticizer A 37.0 NaT
364 2020-09-27 49100 False 15007.0 **** 2021-09-18 15:02:56.725555 **** criticizer A 37.0 NaT
下記スクリプトで、チャンネルごとの登録者数および再生回数の折れ線グラフを描画します。
この際、ユーザ間の絶対数の差を補正するため、炎上前1週間の平均が100となるよう登録者数と再生回数を正規化します
import matplotlib.pyplot as plt
from matplotlib import colors
from datetime import timedelta
color_list = list(colors.TABLEAU_COLORS.values()) # プロット用の色
color_list.extend(list(colors.CSS4_COLORS.values()))
# 炎上日
flaming_date = df[df['transferred_name']=='influencer']['flaming_date'][0].to_pydatetime()
# 炎上前後でデータを分けるメソッド
def devide_before_after(df_src, date_col, flaming_date, before_period, after_period):
df_before = df_src[
(df_src[date_col] >= flaming_date - timedelta(days=before_period))
& (df_src[date_col] < flaming_date)]
df_after = df_src[
(df_src[date_col] >= flaming_date)
& (df_src[date_col] < flaming_date + timedelta(days=after_period))]
return df_before, df_after
# 炎上前後の登録者数と再生回数をプロットするメソッド
def plot_before_after(ax, date_col, y_col, df_src, flaming_date, before_period, after_period, c, name):
# 炎上前後でデータを分ける
df_before, df_after = devide_before_after(df_src, date_col, flaming_date, before_period, after_period)
# プロット
ax.plot(df_before[date_col].values, df_before[y_col].values,
c=c, label=f'{name} before', alpha=0.5)
ax.plot(df_after[date_col].values, df_after[y_col].values,
c=c, label=f'{name} after', alpha=1.0)
ax.axvline(x=flaming_date, color='gray')
ax.set_title(y_col)
ax.legend(loc='upper left')
ax.set_xlabel(f'{date_col}')
ax.set_ylabel(f'{y_col}')
# 炎上前週を100として登録者数と再生回数を正規化するメソッド
def normalize_last_week(df_src, flaming_date):
df_last_week = df_src[
(df_src['date'] >= flaming_date - timedelta(days=7))
& (df_src['date'] < flaming_date)]
subscriber_mean = df_last_week['subscriber_count'].mean() # 前週平均登録者
view_mean = df_last_week['view_count'].mean() # 前週平均再生回数
df_src['subscriber_norm'] = df_src['subscriber_count'] / subscriber_mean * 100 # 登録者数の正規化
df_src['view_norm'] = df_src['view_count'] / view_mean * 100 # 再生回数の正規化
return df_src
# プロット用のaxes
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前週を100として登録者数と再生回数を正規化
df_ch = normalize_last_week(df_ch, flaming_date=flaming_date)
# 正規化したチャンネル登録者数をプロット
plot_before_after(ax=axes[0], df_src=df_ch,
date_col='date', y_col='subscriber_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 正規化した再生数をプロット
plot_before_after(ax=axes[1], df_src=df_ch,
date_col='date', y_col='view_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 図中に炎上日をプロット
axes[0].text(flaming_date, axes[0].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
axes[1].text(flaming_date, axes[1].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
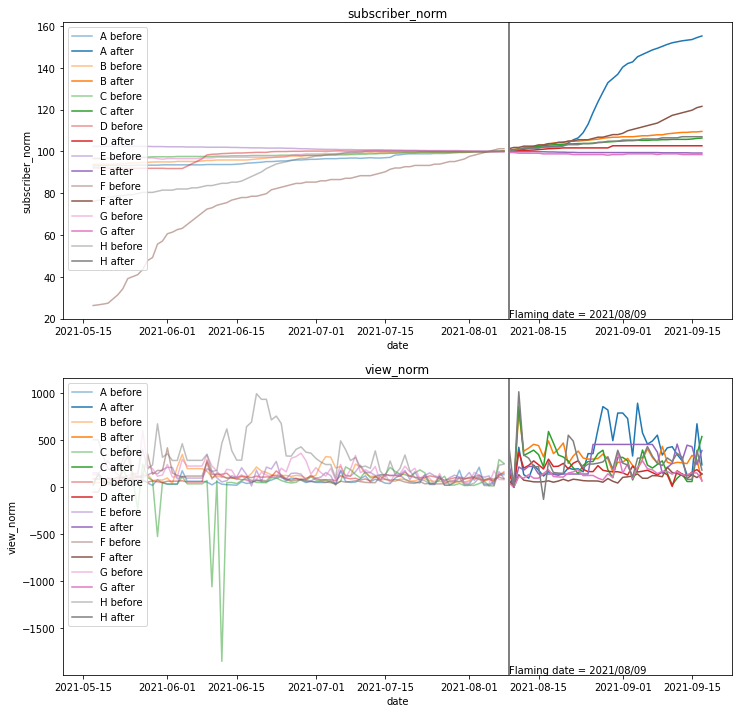
再生回数がマイナスとなる異常値(動画を削除したことに起因)があるので、ゼロで埋めます。
また、削除した動画を再アップロードすると再生回数が激増(炎上後は火消しのために動画の削除と再アップを繰り返す事例が多い)する異常値が発生するので、
「マイナス再生回数から30日以内に、中央値の10倍を超える再生回数があった場合は、中央値で補正する」
という処理も加えます
def modify_minus_view(df_ch, y_col, date_col):
"""再生回数がマイナスのデータをゼロに&30日以内に通常の10倍以上のデータがあれば補正"""
minus_idx = df_ch[df_ch[y_col] < 0].index # 再生回数がマイナスのインデックス
df_ch.loc[minus_idx, y_col] = 0 # 再生回数がマイナスのデータをゼロに補正
for idx in minus_idx:
minus_date = df_ch[date_col].at[idx].to_pydatetime()
# マイナスから30日以内の中央値
median_minus_month = df_ch[(df_ch[date_col] > minus_date)
& (df_ch[date_col] <= minus_date + timedelta(days=30))
][y_col].median()
# マイナスから30日以内で再生回数が中央値の10倍を超えたら中央値で補正
df_ch.loc[(df_ch[date_col] > minus_date)
& (df_ch[date_col] <= minus_date + timedelta(days=30))
& (df_ch[y_col] > median_minus_month * 10),
y_col] = median_minus_month
return df_ch
# 再生回数がマイナスのデータ&直後の異常データを補正
df_criticizer = df_criticizer.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週を100として登録者数と再生回数を正規化
df_criticizer = df_criticizer.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, flaming_date))
# プロット用のaxes
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 正規化したチャンネル登録者数をプロット
plot_before_after(ax=axes[0], df_src=df_ch,
date_col='date', y_col='subscriber_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 正規化した再生数をプロット
plot_before_after(ax=axes[1], df_src=df_ch,
date_col='date', y_col='view_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 図中に炎上日をプロット
axes[0].text(flaming_date, axes[0].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
axes[1].text(flaming_date, axes[1].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
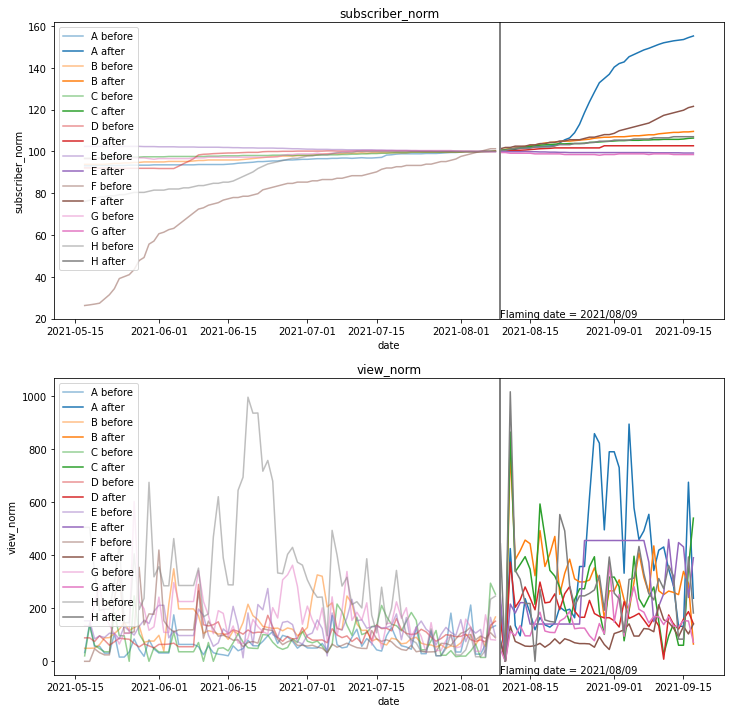
再生回数はばらつきが大きいですが、登録者数(上のグラフ)・再生回数(下のグラフ)ともに炎上(灰色の縦線)を境に増えているようように見えます
再生回数のスペクトル解析と平均処理
再生回数の日変動が大きいため、変動に周期性がないかをスペクトル解析で分析します
import numpy as np
# 全チャンネルで日ごとに平均をとる
view_counts_mean = df_criticizer.groupby('date')['view_norm'].mean().values
# ハミング関数で両端を滑らかに
view_counts_hamming = (view_counts_mean - np.mean(view_counts_mean)) * np.hamming(len(view_counts_mean))
# フーリエ変換
dft = np.fft.fft(view_counts_hamming)
freq = np.fft.fftfreq(len(view_counts_mean), d=1.0)
# 変換結果をプロット
fig, axes = plt.subplots(4, 1, figsize=(10, 15))
axes[0].plot(range(len(view_counts_mean)), view_counts_mean)
axes[0].set_title('view_count')
axes[0].set_xlabel('date')
axes[1].plot(range(len(view_counts_mean)), view_counts_hamming)
axes[1].set_title('hamming')
axes[1].set_xlabel('date')
axes[2].plot(1/freq[1:int(len(view_counts_mean) / 2)], abs(dft[1:int(len(view_counts_mean) / 2)]), c='orange')
axes[2].set_title('FFT')
axes[2].set_xscale('log')
axes[2].set_xlabel('date')
axes[3].plot(1/freq[1:int(len(view_counts_mean) / 2)], abs(dft[1:int(len(view_counts_mean) / 2)]), c='darkorange')
axes[3].set_title('FFT 1-10 days')
axes[3].set_xlim(1, 10)
axes[3].set_xlabel('date')
plt.tight_layout()
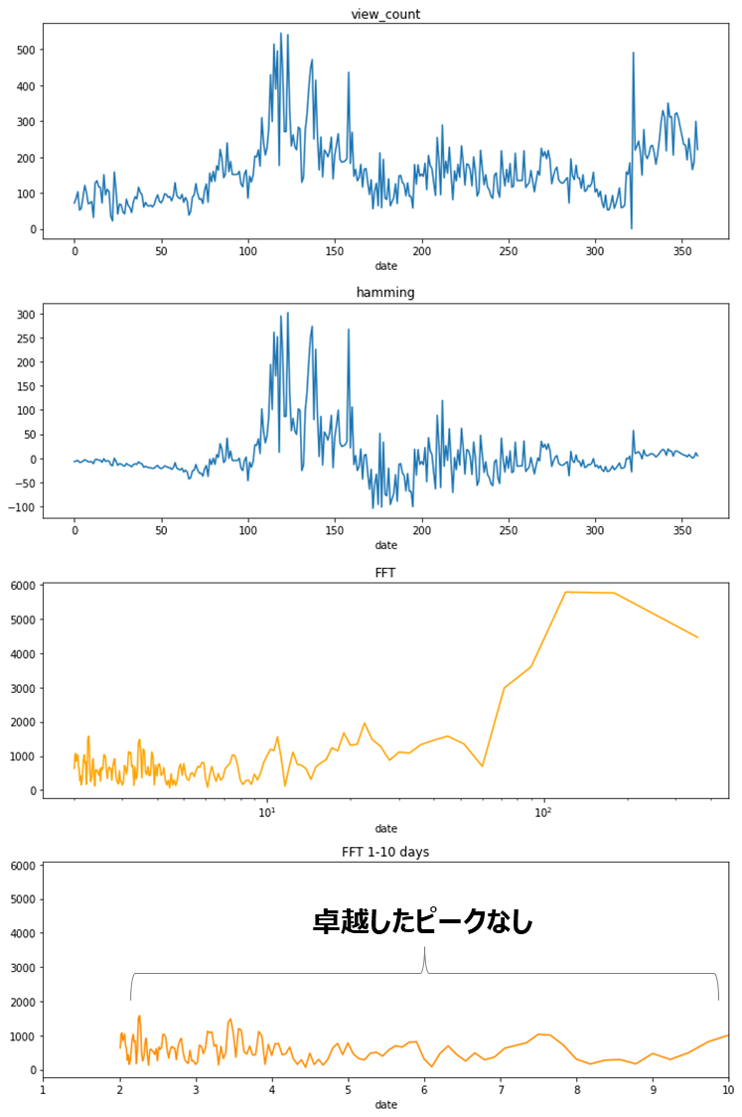
1週間や1ヵ月単位での規則性を期待していましたが、7日や30日付近に卓越したピークはなく、目立った周期性はなさそうです。
ひとまず長期的な変動が見やすいよう、1週間単位で平均をとって再プロットします
import math
# 炎上日からの経過日、経過週を計算
import math
# 炎上日からの経過日、経過週を計算
df_criticizer['date_diff'] = (df_criticizer['date'] - flaming_date).dt.total_seconds() / 3600 / 24
df_criticizer['week_diff'] = df_criticizer['date_diff'].map(lambda x: math.floor(x/7))
# 週ごとの平均登録者数と平均再生回数を求める
df_criticizer_grby_week = df_criticizer.groupby(['transferred_name', 'week_diff']).agg({
'date': 'min',
'subscriber_norm': 'mean',
'view_norm': 'mean'
})
# プロット用のaxes
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# チャンネルごとにループ
for i, (name, df_ch_grby_week) in enumerate(df_criticizer_grby_week.groupby('transferred_name')):
# 炎上前後の登録者数プロット
plot_before_after(ax=axes[0], df_src=df_ch_grby_week,
date_col='date', y_col='subscriber_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 炎上前後の再生回数プロット
plot_before_after(ax=axes[1], df_src=df_ch_grby_week,
date_col='date', y_col='view_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
axes[0].set_ylim(0,)
axes[1].set_ylim(0,)
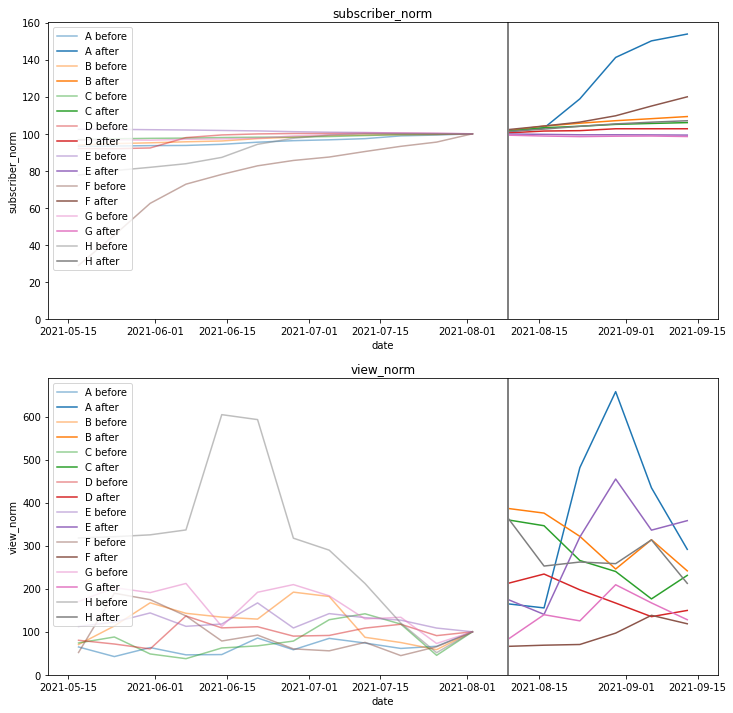
これで変化が見やすくなりました。この時点でチャンネル登録者数・再生回数共に、明らかに炎上日(灰色の線)を境に増加しているように見えます。
これだけだと定性的で「明らかじゃなくてあなたの感想ですよね?」と言われてしまいそうなので、定量的な分析を進めていきます
・定量分析1:炎上前後の増加率
単純な増加量を比較するため、以下の統計量を算出して散布図でプロットします
チャンネル登録者数:炎上日の登録者数に対する、炎上40日後の増加率[%]
再生回数:炎上前40日間の平均に対する、炎上後40日の平均の増加率[%]
(再生回数はばらつきが大きいので、平均をとりました)
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list = [] # 登録者数増加率格納用
view_increase_list = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=AFTER_FLAMING, after_period=AFTER_FLAMING)
# 炎上日から分析対象日数(AFTER_FLAMING)後までの登録者数の増加率
subscribers_flaming_day = df_before['subscriber_count'].iloc[-1]
subscribers_after_flaming = df_after['subscriber_count'].iloc[-1]
subscriber_increase_ratio = (subscribers_after_flaming / subscribers_flaming_day) * 100 - 100
subscriber_increase_list.append(subscriber_increase_ratio)
# 炎上前と炎上後の再生回数増加率
views_before_flaming = df_before['view_count'].mean()
views_after_flaming = df_after['view_count'].mean()
view_increase_ratio = (views_after_flaming / views_before_flaming) * 100 - 100
view_increase_list.append(view_increase_ratio)
# 散布図プロット
ax.scatter(subscriber_increase_ratio, view_increase_ratio,
c=color_list[i], label=name)
ax.legend(loc='upper left')
xlim = ax.get_xlim()[1]
ylim = ax.get_ylim()[1]
ax.set_xlim(-xlim, xlim)
ax.set_ylim(-ylim, ylim)
ax.set_xlabel('Subscriber increase [%]')
ax.set_ylabel('View increase [%]')
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list)}%')
チャンネル登録者数増加率平均=12.250737582632588%
再生回数数増加率平均=133.82378782101105%
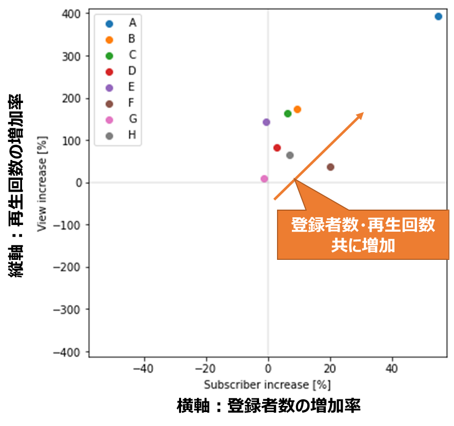
ほぼすべてのチャンネルが、登録者数、再生回数共に増加している(散布図上の第一象限にある)ことが分かります。
参考までに、炎上が発生していない期間での増加率をプロットしたところ、
以下のようになりました。
チャンネル登録者数増加率平均=3.787839959591375%
再生回数数増加率平均=-7.220381207322854%
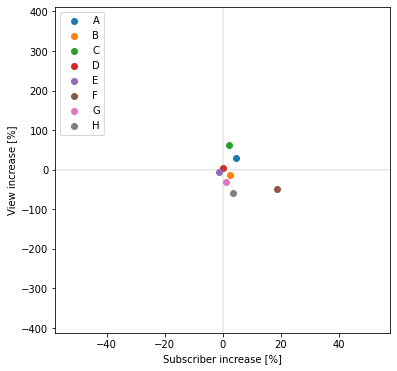
第一象限以外に存在するデータが多く、再生回数増加率に関しては平均でマイナスとなっています。
このことから、チャンネル登録者数、再生回数共に、炎上発生時は通常時と比べて高い増加率となることが確認できました。
・定量分析2:時系列分析
前節は単純に「炎上前」「炎上後」の2区間に分けて増加率を計算しましたが、
今回のような時系列データでは、細かく期間を区切って周期性から長期のトレンドまでを包括して考慮することで精度向上を目指す、**「時系列分析」**と呼ばれる手法がよく使われます。
今回のデータでは、炎上前から上昇トレンド(チャンネルA, C)、あるいは下降トレンド(チャンネルF, H)を持つデータも存在するため、このトレンドから推定される予測値と、炎上後の実測値との差分をとることで、トレンドを差し引いた炎上起因の増加率を算出することを目指します。
モデルの選定
時系列データの分析には状態空間モデルやDeep Learning (RNN)など多種多様な手法が存在しますが、今回は伝統的な時系列分析手法であるARモデルをベースとした手法を検討します。
(ARモデルの詳細はこちらの書籍を参照ください)
・ARモデル
ARモデル (Autoregressive model, 自己回帰モデル)とは、現在の値$y_t$が、過去の値$y_{t-i}$とホワイトノイズ$\epsilon_t$(≒正規分布に従うランダムなばらつき)を用いて以下の式で表されるモデルです。
y_t = c + \sum_{i=1}^{p} \phi_i y_{t-i} + \epsilon_t
ざっくり解釈すると、「現在の値 = 定数項 + p個前までの値の定数倍の和 + ノイズ」で表されるモデルと言えます。
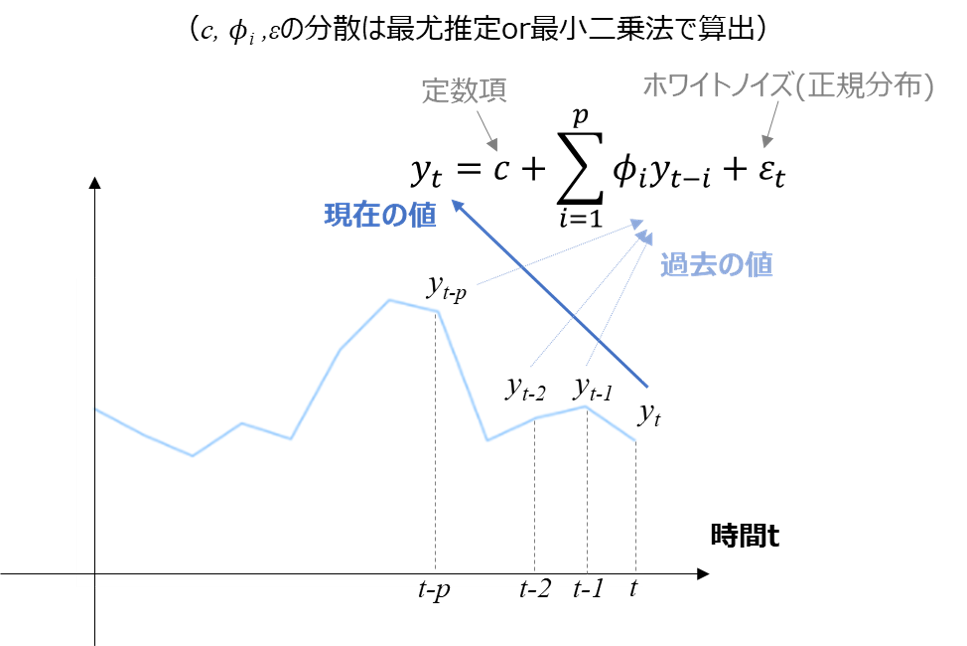
ARモデルのメリットとして、実際の時系列データで頻出する以下の特徴を表現できることが挙げられます。
①経過時間によりデータの影響度が変わる(多くの場合、時間的に近いデータの影響が大きい)
②周期性を表現できる(周期をTとしたときT次の自己相関が大きくなる)
これらの特徴は、係数φにより自己相関が決まることに起因します。
自己相関についてはこちらやこちらの記事で分かりやすく説明されています。
今回のデータにおいては、特徴②は前述のスペクトル分析で確認できませんでしたが、特徴①に関しては動画のアップロードや炎上とは無関係なバズにより時間的に近いデータの影響が大きい事が想定され、この点ではARモデルを採用する事は理にかなっているように見えます。
・ARモデルと定常性
今回のデータは上昇・下降トレンドを考慮した予測を行いたいので、上記①、②以外に**「③長期的なトレンドを表現できる」**ことが非常に重要です。
ここで問題となってくるのが、ARモデルの定常性です。
時系列モデルにおける定常性(弱定常)とは、「平均と自己共分散が時間tに依存しない」ことを表します。
ARモデルを統計的に扱う(最尤推定等を行う)ためにはこの定常性を満たす必要があり、
定常性の条件である「平均が時間tに依存しない = トレンドを持たない」ことは、条件③と矛盾するため、今回の分析目的にARモデルは適していないと言えそうです。
参考までに、ARモデルが定常となる条件は、以下の特性多項式の解が全て|λ|<1を満たすことです。
\lambda ^p -\phi _1 \lambda ^{p-1} – \cdots – \phi _{p-1} \lambda – \phi _p =0
・MAモデル
MAモデル (Moving-average model)はARモデルと並ぶ時系列分析の基礎的なモデルで、現在の値$y_t$が過去のホワイトノイズ$\epsilon_t$(≒正規分布に従うランダムなばらつき)を用いて以下の式で表されるモデルです。
y_t = \mu + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}
ARモデルは過去の値の和で現在の値が決まるモデルでしたが、
MAモデルは過去のホワイトノイズの和で現在の値が決まるモデルとなります。
詳細はこちらが詳しいですが、MAモデルもARモデルと同様に特徴①、特徴②のメリットを保持しており、
また定常性を持ちます。
よってMAモデルも今回の分析目的には不適切と言えそうです。
・ARMAモデル
実用上よく使われるモデルとして、ARモデルとMAモデルを組み合わせて表現力を向上させたARMAモデルが挙げられます。
ARMAモデルは以下の式で表されます(p次ARモデルとq次MAモデルの和)
y_t = c + \epsilon_t + \sum_{i=1}^{p} \phi_i y_{t-i} + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}
構成するARモデル、MAモデルが定常性を持つとき、ARMAモデルも同様に定常性を持ちます。
ARMAモデルは定常データであれば高性能を発揮する便利なモデルですが、今回は長期トレンドを考慮したいので、不適と言えそうです。
・ARIMAモデル
似たようなモデル名がたくさん出てきて疲れたかと思いますが、これが最後です。
今まで紹介した3モデルは定常性を前提としており今回の分析には不適でしたが、
ARIMAモデルは非定常なデータを表現できるモデルであり、以下の式で表されます
y_t - y_{t-d} = c + \epsilon_t + \sum_{i=1}^{p} \phi_i y_{t-i} + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}
ARMAモデルとの違いは左辺のみで、「現在値 - d系列前の値」がARMAモデルに従うモデルと言えます。
このように、データ同士のd階差分が定常性を持つ「d次の和分過程」と呼び、特にd=1のときを「単位根過程」と呼び、トレンドを持つデータの表現方法として多用されています。
(非線形なトレンドや分散が変動する場合、対数変換等を実施する事で単位根過程に落とし込むことや、季節性を持つ場合は派生であるSARIMAモデルの利用がよく行われます)
このようにARIMAモデルは周期性、トレンド、ノイズを全て表現できる優秀なモデルですが、p,d,qという3種のパラメータを持ち、その推定に手間が掛かることが難点です。
パラメータの推定方法については後述するので、まずはARIMAモデルを採用して実装を進めていきます
ARIMAモデルの実装
前置きが長くなりましたが、ARIMAモデルを実装していきます。
・階差と自己相関の確認
まずはパラメータd(和分過程の次数)およびp(ARモデルの次数)、q(MAモデルの次数)の最大値を推定するため、階差をとって自己相関コレログラムをプロットします。
from statsmodels.graphics.tsaplots import plot_acf
n_channels = df_criticizer['transferred_name'].nunique()
fig, axes = plt.subplots(n_channels, 2, figsize=(12, n_channels*3)) # プロット用のaxes
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後データを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上前データの登録者数&再生回数の自己相関コレログラム表示
plot_acf(df_before['subscriber_norm'], lags=31, ax=axes[i][0],
title=f'subscriber_{name}')
plot_acf(df_before['view_norm'], lags=31, ax=axes[i][1],
title=f'view_{name}')
plt.tight_layout()
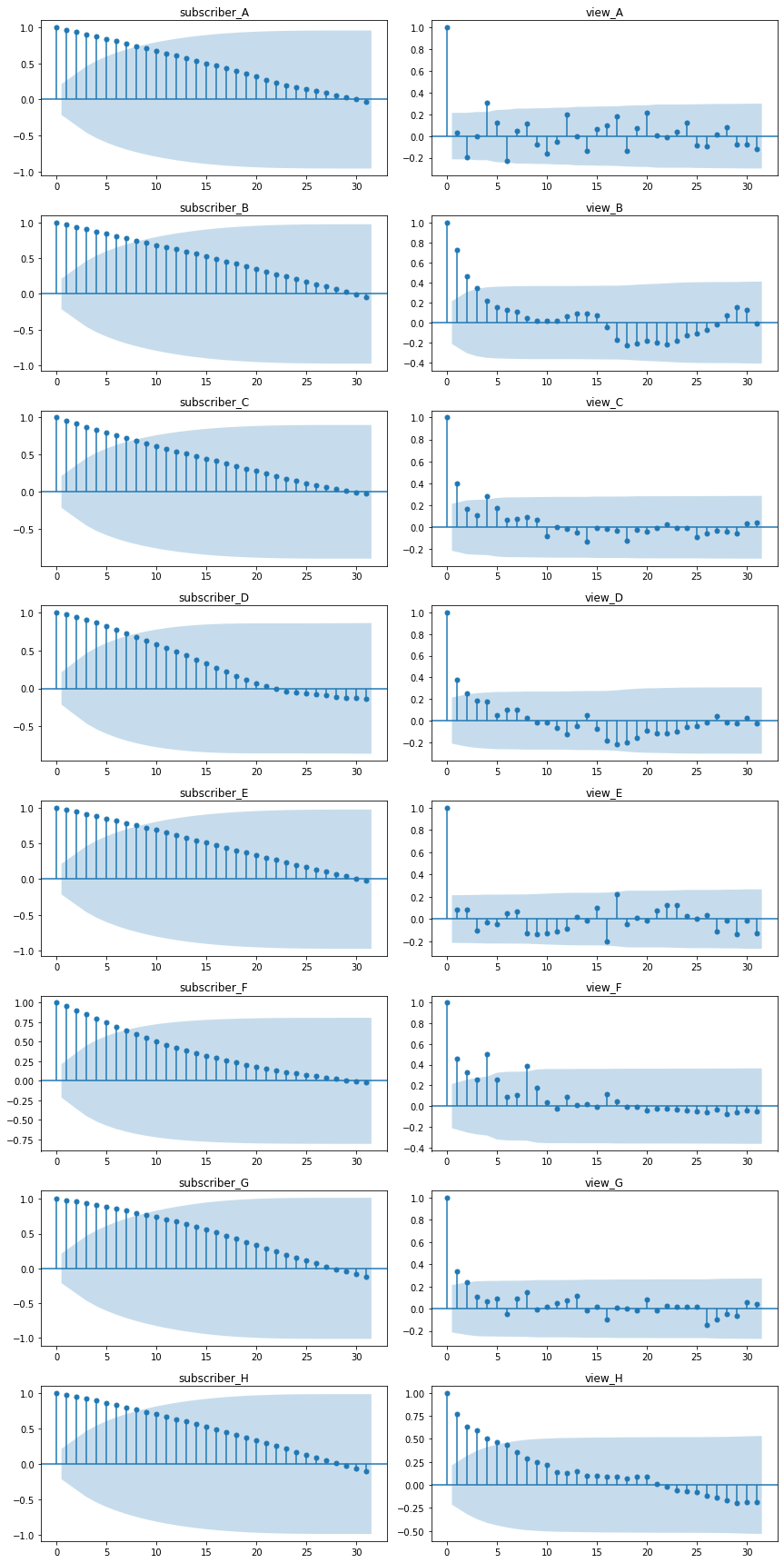
自己相関コレログラムの解釈方法ですが、以下の1, 2を主に評価します。
- 減衰の速さから、階差選択の妥当性を評価(減衰が遅いとトレンドが残っており、定常モデルとして不適)
- 突発的なピークから、周期性を評価(前述のスペクトル解析と近い)
1に関しては、特に登録者数(subscriber)の階差を取る前の自己相関コレログラムの減衰が遅く、非定常のため階差を取る必要がある(ARMAモデルではなくARIMAモデルを検討する必要がある)と判断されそうです
2に関しては、チャンネルによっては4日(動画のアップロード間隔?)のピークが見られます。
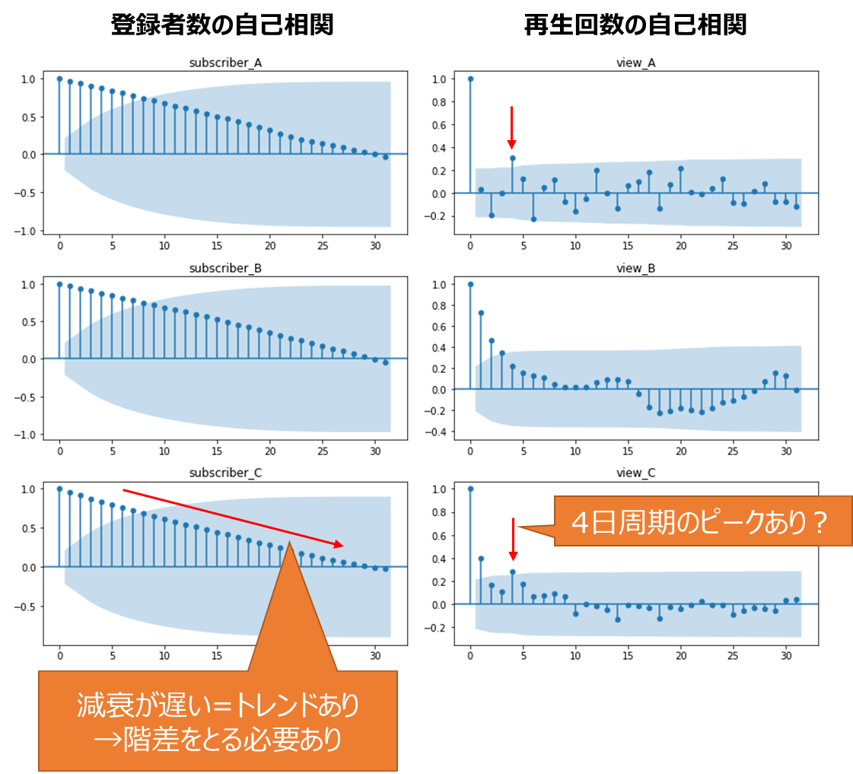
これらが階差をとることでどのように変化するかを確認します。
まずは登録者数の1~3階差分をプロットしてみます
from statsmodels.graphics.tsaplots import plot_acf
n_channels = df_criticizer['transferred_name'].nunique()
def plot_diff_acf(x, lags, axes_diff, axes_acf, name):
"""差分の自己相関コレログラム描画用メソッド"""
# 階差1のデータプロット
axes_diff[0].plot(np.diff(x))
axes_diff[0].set_title(f'1st_order_correlation_{name}')
# 階差1の自己相関コレログラム
plot_acf(np.diff(x),
lags=lags, ax=axes_acf[0],
title=f'1st_order_{name}')
# 階差2のデータプロット
axes_diff[1].plot(np.diff(np.diff(x)))
axes_diff[1].set_title(f'2nd_order_correlation_{name}')
# 階差2の自己相関コレログラム
plot_acf(np.diff(np.diff(x)),
lags=lags, ax=axes_acf[1],
title=f'2nd_order_{name}')
# 階差3のデータプロット
axes_diff[2].plot(np.diff(np.diff(np.diff(x))))
axes_diff[2].set_title(f'3rd_order_correlation_{name}')
# 階差3の自己相関コレログラム
plot_acf(np.diff(np.diff(np.diff(x))),
lags=lags, ax=axes_acf[2],
title=f'3rd_order_{name}')
fig, axes = plt.subplots(n_channels * 2, 3, figsize=(18, n_channels*6)) # プロット用のaxes
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後データを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 差分の自己相関コレログラム描画
plot_diff_acf(x=df_before['subscriber_norm'].to_numpy(), lags=31,
axes_diff=axes[i*2], axes_acf=axes[i*2+1], name=name)
plt.tight_layout()
(長いのでAとBのみ表示します)
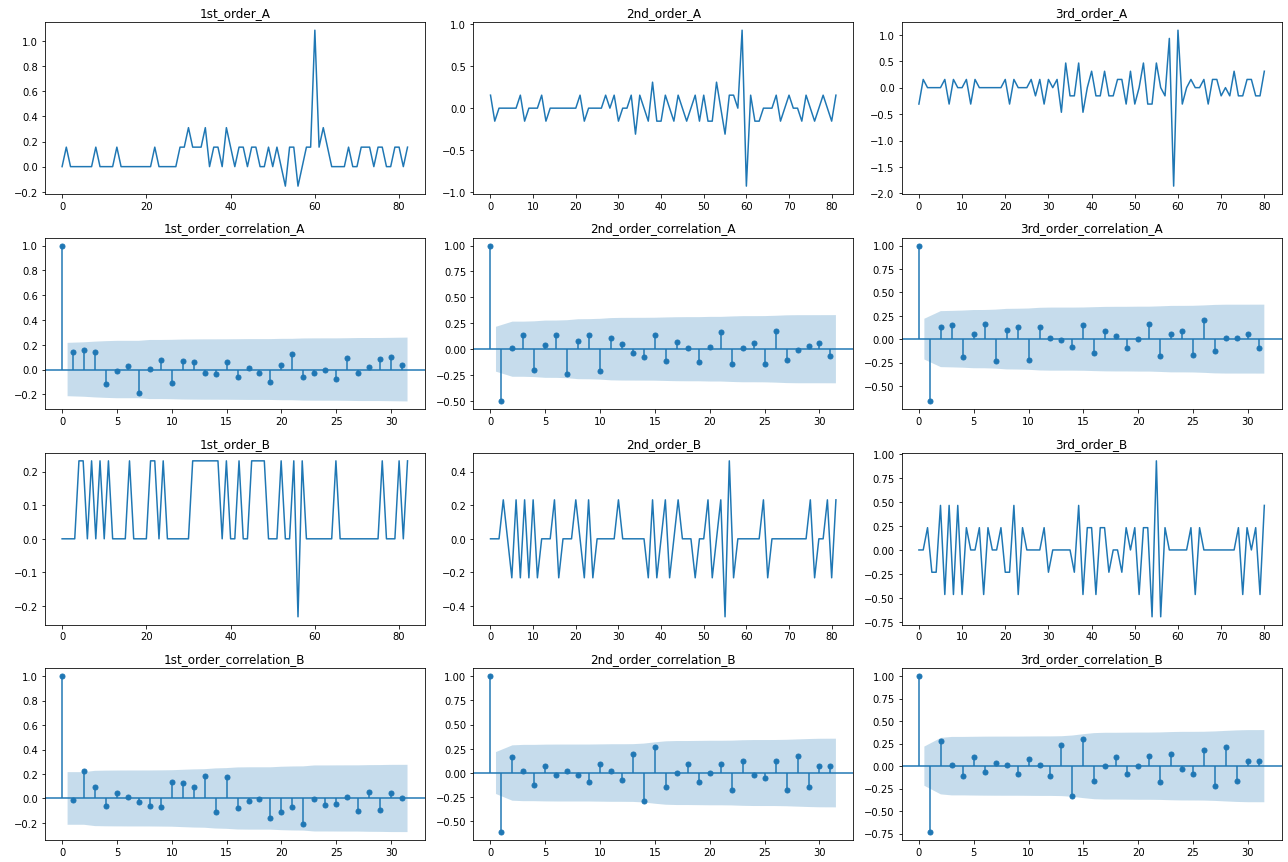
2階差分(左から2列目グラフ)を取る事で、上下対称の変動かつコレログラムの減衰も速く、定常に至っていると確認できます。
よって登録者数に関してはd=2、周期性は確認できないので、デフォルト値であるpの最大値=4, qの最大値=2を採用します。
再生回数に関しても同様にプロットします
from statsmodels.graphics.tsaplots import plot_acf
n_channels = df_criticizer['transferred_name'].nunique()
fig, axes = plt.subplots(n_channels * 2, 3, figsize=(18, n_channels*6)) # プロット用のaxes
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後データを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 差分の自己相関コレログラム描画
plot_diff_acf(x=df_before['view_norm'].to_numpy(), lags=31,
axes_diff=axes[i*2], axes_acf=axes[i*2+1], name=name)
plt.tight_layout()
(長いので周期性に特徴のあったAとFのみ表示します)
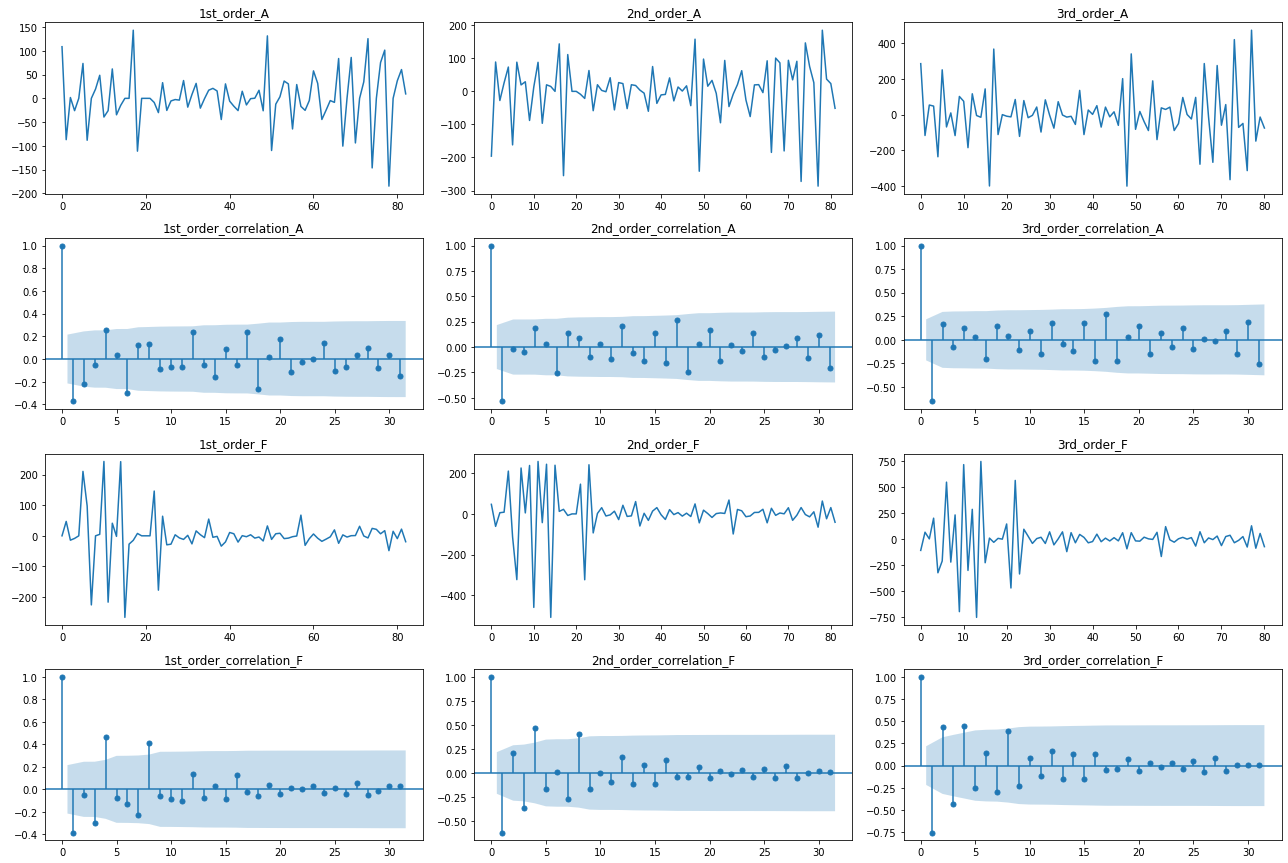
1階差分(一番左の列のグラフ)の時点で上下対称の変動かつコレログラムの減衰も速いので、d=1を採用します。
周期性に関しては、4日周期が有意水準(図中の薄青で塗りつぶされた範囲)を超えるチャンネルが見られるので、p, qの最大値=4を採用します。
(8日周期は4日周期の倍に起因していそうなので無視します。このような倍周期の影響を軽減したい場合、自己相関ではなく「偏自己相関」のコレログラムを使用する事もあります)
pとqどちらを調整するかを自己相関と偏自己相関のコレログラムを見て決めてしまう方法もあるようですが、今回のようなノイズの多いデータでは判断が難しいため、次節でp,q両方を調節して性能指標をもって最適値を推定します。
・パラメータpおよびqの自動推定
パラメータdと、pとqの最大値が定まったので、この範囲内で性能が最大となるpとqの組合せを選択します。
性能の評価には「AIC」や「BIC」という指標を用います。
厳密な定義は奥が深いので専門書を参照頂きたいですが、これらの指標はざっくり言うと
「モデルの単純さ(過学習の少なさ)と、データに対するフィッティング性能のバランスを評価する指標」
と言え、値が小さいほど優れたモデルとして解釈できます。
AICとBICの差としては、BICの方がモデルの単純さを重視する傾向があります。
Pythonにおいては、statsmodels.tsa.stattools.arma_order_select_icメソッドで、指定した範囲内で指標が最も良くなるp, qの値を自動選択できます。
名称の通りARIMAではなくARMA用のメソッドのため、事前にd回分階差をとってから適用する必要があります
from statsmodels.tsa.stattools import arma_order_select_ic
D_SUBSCRIBER = 2 # ARIMAモデルのパラメータd(階差の数)
P_MAX_SUBSCRIBER = 4 # ARIMAモデルのパラメータpの最大値
Q_MAX_SUBSCRIBER = 2 # ARIMAモデルのパラメータqの最大値
def optimize_arima_pq(x, d, p_max, q_max):
"""ARIMAモデルのpとqを推定するメソッド"""
diff = x.copy()
for i in range(d): # d回差分をとる
diff = diff.diff()
diff = diff.dropna() # nanを削除
# diffが全て0なら、p=0, q=0を返す
if diff.nunique() == 1 and diff.iat[0] == 0:
return 0, 0
# ARMAのパラメータ推定
res = arma_order_select_ic(diff, ic='aic', trend='nc',
max_ar=p_max, max_ma=q_max)
print(res['aic'])
print(f'best p={res["aic_min_order"][0]}, q={res["aic_min_order"][1]}')
return res['aic_min_order']
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後データを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 時間がindexのSeriesを作成
x_series = df_before[['subscriber_norm', 'date']]
x_series = x_series.set_index('date')['subscriber_norm']
# パラメータpとqの推定
best_p, best_q= optimize_arima_pq(x=x_series,
d=D_SUBSCRIBER,
p_max=P_MAX_SUBSCRIBER,
q_max=Q_MAX_SUBSCRIBER)
実行すると、以下のように縦軸p、横軸qで総当たりのスコアが表示されます。
0 1 2
0 NaN -73.692755 -72.602024
1 -57.084138 -72.853205 -71.871767
2 -63.674868 -72.362302 -70.626007
3 -61.705629 -71.272884 -70.212768
4 -62.412732 -71.663323 -67.211781
best p=0, q=1
上記の例(チャンネルAの登録者数データ)では、p=0, q=1スコアが最も良いことがわかります。
これらを対象全チャンネルにループ適用することで、それぞれp, qの最適値を求めます。
・モデルの作成と予測結果の可視化 (登録者数)
パラメータが確定できたので、
statsmodels.tsa.arima.model.ARIMAクラスを使用してARIMAモデルを作成します。
なお、多くの日本語記事では古いバージョンのstatsmodels.tsa.arima_model.ARIMAを使用していますが、2021/9現在は非推奨となっているのでご注意ください。
以下のコードでは、
上記パラメータ推定 → ARIMAモデル作成 → モデルによる予測値と炎上後実測値の比較プロット
の一連の流れを連続実行しています
from statsmodels.tsa.arima.model import ARIMA
D_SUBSCRIBER = 2 # ARIMAモデルのパラメータd(階差の数)
P_MAX_SUBSCRIBER = 4 # ARIMAモデルのパラメータpの最大値
Q_MAX_SUBSCRIBER = 2 # ARIMAモデルのパラメータqの最大値
ALPHA = 0.05 # 区間予測の有意水準
def plot_arima_predict(x, order, predict_start, predict_end, ax, alpha=None):
"""推定したパラメータでARIMAモデル作成し、予測結果をプロット"""
# ARIMAモデル作成
model = ARIMA(x, order=order)
res = model.fit() # 学習
print(res.summary())
# モデルで将来予測
pred = res.get_prediction(start=predict_start,
end=predict_end,
dynamic=False)
pred_mean = pred.predicted_mean
pred_ci = pred.conf_int(alpha=alpha)
ax.plot(x, label='observed')
ax.plot(pred_mean, label='predict', c='green')
if alpha is not None:
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1],
color='green', alpha=0.2)
return pred_mean
def compare_pred_and_flaming(df_src, date_col, y_col, ax,
flaming_date, before_period, after_period,
d, p_max, q_max, alpha):
"""ARIMAモデルで予測して炎上後の実データと比較プロットするメソッド"""
# 炎上前後データを抜き出し
df_before, df_after = devide_before_after(df_src, date_col, flaming_date,
before_period=before_period, after_period=after_period)
# 時間がindexのSeriesを作成
x_series = df_before[[y_col, date_col]]
x_series = x_series.set_index(date_col)[y_col]
# パラメータpとqの推定
best_p, best_q= optimize_arima_pq(x=x_series,
d=d,
p_max=p_max,
q_max=q_max)
# 推定したパラメータでARIMAモデル作成し、予測結果をプロット
pred_mean = plot_arima_predict(x=x_series, order=(best_p, d, best_q),
predict_start=flaming_date,
predict_end=flaming_date + timedelta(days=after_period-1),
ax=ax, alpha=alpha)
# 実際の炎上後の推移をプロット
ax.plot(df_after[date_col].values, df_after[y_col].values,
label='after flaming', c='red')
ax.legend(loc='upper left')
ax.set_title(f'{y_col}_{name}')
ax.text(x_series.index.min(), ax.get_ylim()[0],
f'p={best_p}\nq={best_q}', verticalalignment='bottom', horizontalalignment='left')
return pred_mean
pred_subscribers = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# ARIMAモデルで予測して炎上後の実データと比較プロット
pred_subscribers[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
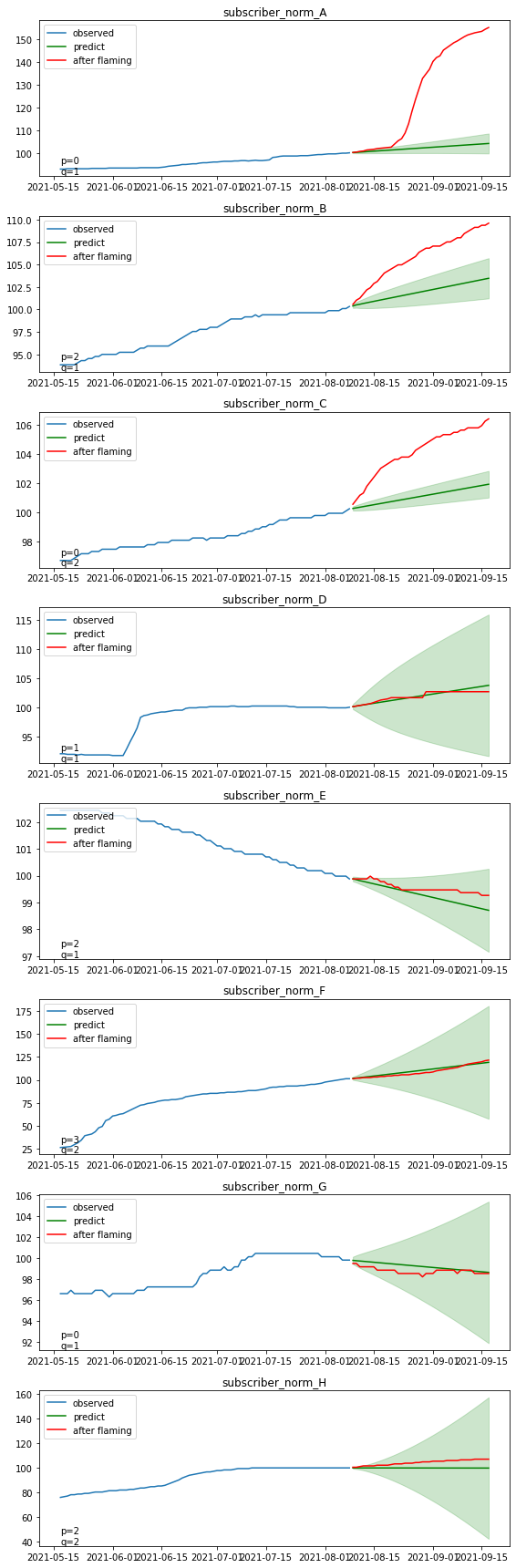
青線:炎上前の実際の登録者数の推移(モデルの学習データ)
緑線:モデルにより推定された予測値の平均(炎上がなかった場合の予測推移)
薄い緑:モデルの区間推定の範囲(95%信頼区間)
赤線:炎上後の実際の登録者数推移
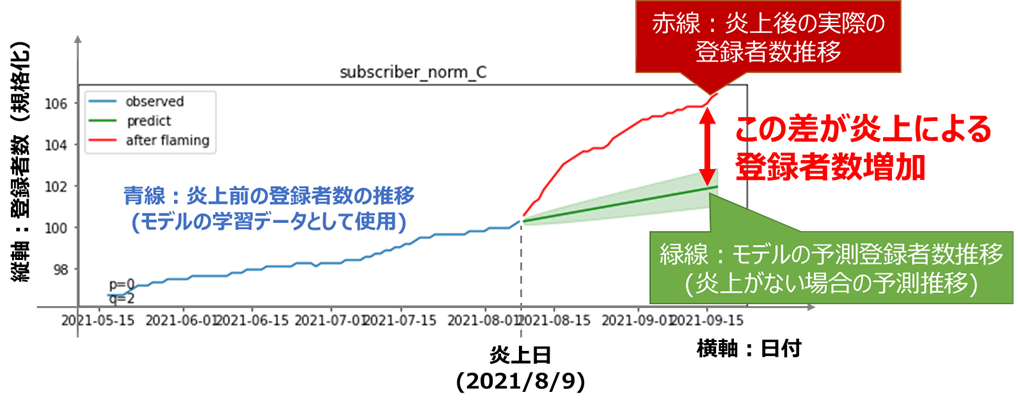
緑の線はうまくトレンドを捉えて予測できていそうです。
赤線と緑線の差が炎上による登録者数の増加に相当しますが、
基本的にどのチャンネルも赤線が緑線より上に来ており、炎上の関連動画をアップロードしたことが、登録者数の増加につながったと解釈できそうです。
特に上位3チャンネル(A, B, C)は信頼区間を大きく超えて上昇しており、炎上をきっかけに有意水準を超える多数の登録者を獲得したと言えそうです。
・モデルの作成と予測結果の可視化(再生回数)
再生回数についても同様に、炎上がなかった場合の推移を予測します
D_VIEW = 1 # ARIMAモデルのパラメータd(階差の数)
P_MAX_VIEW = 4 # ARIMAモデルのパラメータpの最大値
Q_MAX_VIEW = 4 # ARIMAモデルのパラメータpの最大値
pred_views = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
pred_views[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='view_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_VIEW, p_max=P_MAX_VIEW, q_max=Q_MAX_VIEW, alpha=ALPHA)
plt.tight_layout()
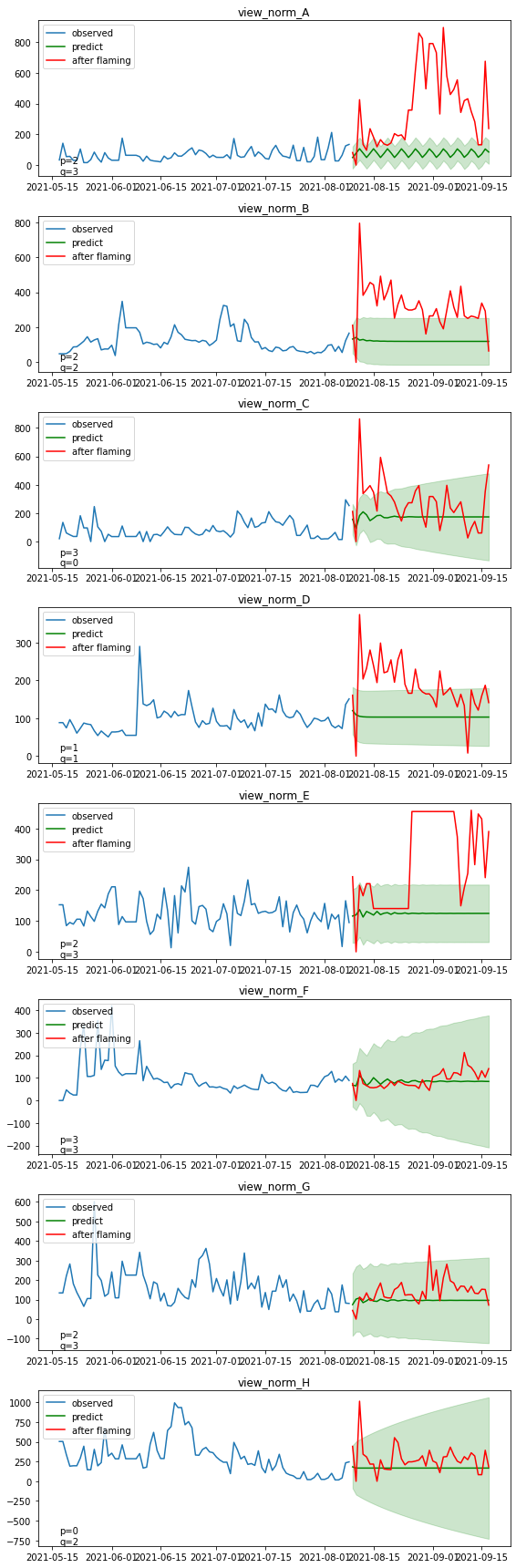
上位5チャンネル(A~E)は、信頼区間を上回る再生回数を断続的に稼げていることが分かります。
予測値からの増加率
定量分析1のときと同様に、横軸にチャンネル登録者数の増加率、縦軸に再生回数の増加率をとって散布図でプロットします。
それぞれの増加率は以下のように定義します(基本的には定量分析1と同じ考え方)
チャンネル登録者数:炎上40日後の登録者数予測値に対する、実測値の増加率[%](グラフ右端の赤線÷緑線)
再生回数:炎上後40日間の再生回数予測値平均に対する、実測値平均の増加率[%](グラフの赤線の平均÷緑線の平均)
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list = [] # 登録者数増加率格納用
view_increase_list = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_criticizer.groupby('transferred_name')):
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list.append(subscriber_increase_ratio)
view_increase_list.append(view_increase_ratio)
ax.set_xlim(-xlim, xlim)
ax.set_ylim(-ylim, ylim)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list)}%')
チャンネル登録者数増加率平均=8.467273875715309%
再生回数数増加率平均=116.56891407106986%
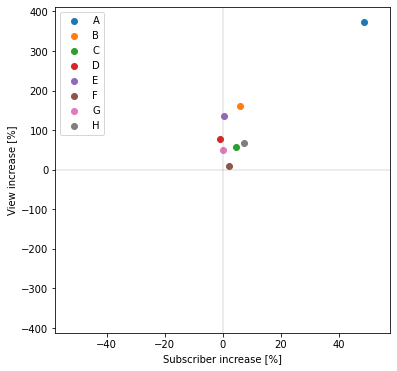
ほぼ全てのチャンネルが、登録者数、再生回数共に増加している(散布図上の第一象限にある)ことが分かりました。
特に再生回数に関しては平均でも倍以上に増えており、収益化していれば相当なメリットが生まれると想像されます。
登録者数・再生回数増加率と批評動画アップロード数の比較
ここまで読んで
「炎上関係の批評動画をアップロードする数が多ければ多いほど、登録者数や再生回数は増えるのか?」
に興味を持たれた方も多いかと思います。
そこで横軸に批評動画アップロード数、縦軸に登録者数および再生回数をとって散布図をプロットし、両者に相関関係があるかを確かめました
from seaborn_analyzer import regplot
video_nums = df_criticizer.groupby('transferred_name')['critcizing_videos'].mean().to_numpy()
regplot.linear_plot(video_nums, np.array(subscriber_increase_list),
x_colname='critcizing_videos', plot_scores=False)
plt.ylabel('subscriber_increase_ratio')
plt.show()
regplot.linear_plot(video_nums, np.array(view_increase_list),
x_colname='critcizing_videos', plot_scores=False)
plt.ylabel('view_increase_ratio')
plt.show()
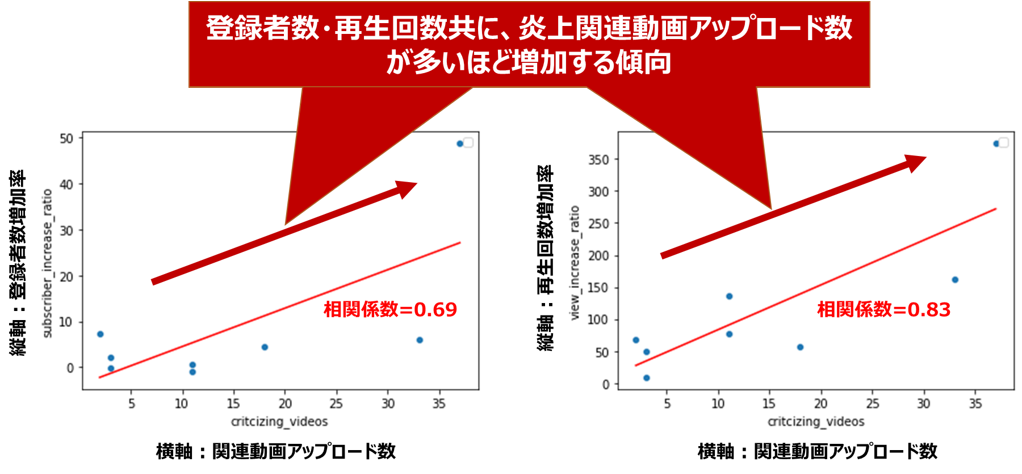
登録者数増加率と動画アップロード数(相関係数=0.69)
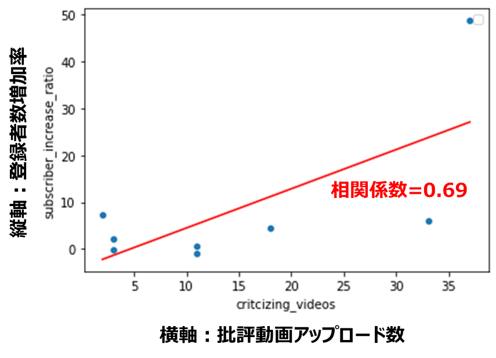
再生回数増加率と動画アップロード数(相関係数=0.83)
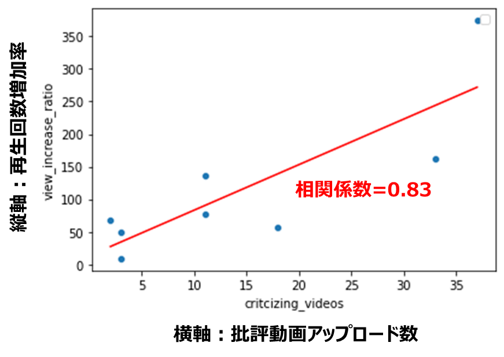
どちらも正の相関関係が見られます。
特に再生回数は相関係数が大きく、批評動画をアップロードする数が多いほど再生回数が稼げるという、なんとも物議を醸しそうな関係が、データから確認できました。
炎上と無関係なチャンネルの分析
前記の分析では炎上を境に批評者のチャンネル登録者数、再生回数が増加することが確認できましたが、
この増加は炎上に対する批評が原因ではなく、炎上とは無関係なビジネス系YouTuber全体の変化により引き起こされている可能性もあります
そこで、
・炎上とは無関係なビジネス系YouTuber20名
・1回のみ炎上関連動画をアップロードしたユーザ(1回だけでも効果があるのか?)
に関しても、同様の分析を行いました。
炎上とは無関係なビジネス系YouTuberの分析
炎上とは無関係なビジネス系YouTuber20名に関して、横軸にチャンネル登録者数の増加率、縦軸に再生回数の増加率をとって散布図でプロットします。
df_business = df[df['classification']=='business'].copy()
# 再生回数がマイナスのデータ&直後の異常データを補正
df_business = df_business.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週が100となるよう規格化
df_business = df_business.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, flaming_date))
n_channels = df_business['transferred_name'].nunique() # チャンネル数
# 登録者数の予測
pred_subscribers_business = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_business.groupby('transferred_name')):
pred_subscribers_business[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 再生回数の予測
pred_views_business = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_business.groupby('transferred_name')):
pred_views_business[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='view_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_VIEW, p_max=P_MAX_VIEW, q_max=Q_MAX_VIEW, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 登録者数と再生回数の予測値からの増加率
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list_business = [] # 登録者数増加率格納用
view_increase_list_business = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_business.groupby('transferred_name')):
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers_business[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views_business[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list_business.append(subscriber_increase_ratio)
view_increase_list_business.append(view_increase_ratio)
ax.set_xlim(-xlim, xlim)
ax.set_ylim(-ylim, ylim)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list_business)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list_business)}%')
チャンネル登録者数増加率平均=1.3043890571297283%
再生回数数増加率平均=20.601634686248772%
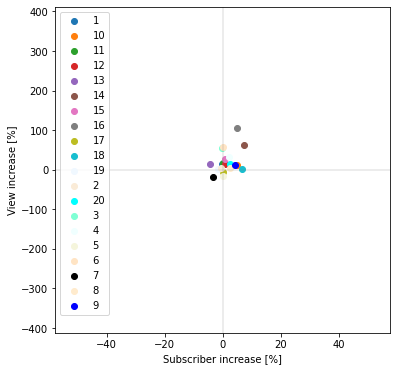
活発に活動しているYouTuberを選定したからか若干の上昇傾向は見られますが、批評者と比べると上昇幅は小さく、散布図の中央付近に点が集まっていることが分かります。
よって批評者の登録者数・再生回数獲得は、ビジネス系YouTuber全体の変化より大きいと言えそうです。
1回のみ炎上関連動画をアップロードしたユーザの分析
1回のみ炎上関連動画をアップロードしたユーザに関して、横軸にチャンネル登録者数の増加率、縦軸に再生回数の増加率をとって散布図でプロットします。
df_one_criticizer = df[(df['classification']=='criticizer')
& (df['critcizing_videos'] == 1)].copy()
# 再生回数がマイナスのデータ&直後の異常データを補正
df_one_criticizer = df_one_criticizer.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週が100となるよう規格化
df_one_criticizer = df_one_criticizer.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, flaming_date))
n_channels = df_one_criticizer['transferred_name'].nunique() # チャンネル数
# 登録者数の予測
pred_subscribers_one = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_one_criticizer.groupby('transferred_name')):
pred_subscribers_one[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 再生回数の予測
pred_views_one = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_one_criticizer.groupby('transferred_name')):
pred_views_one[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='view_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_VIEW, p_max=P_MAX_VIEW, q_max=Q_MAX_VIEW, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 登録者数と再生回数の予測値からの増加率
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list_one = [] # 登録者数増加率格納用
view_increase_list_one = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_one_criticizer.groupby('transferred_name')):
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers_one[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views_one[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list_one.append(subscriber_increase_ratio)
view_increase_list_one.append(view_increase_ratio)
ax.set_xlim(-xlim, xlim)
ax.set_ylim(-ylim, ylim)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list_one)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list_one)}%')
チャンネル登録者数増加率平均=3.074891811040826%
再生回数数増加率平均=-12.52837203657299%
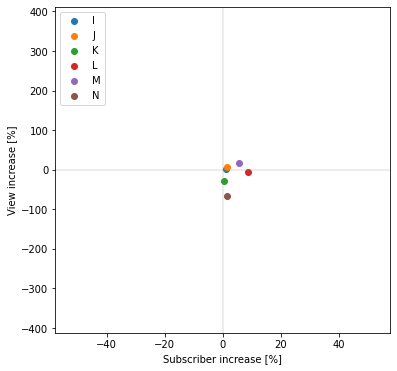
炎上と無関係なビジネス系YouTuberと比較すると、チャンネル登録者数は微増、再生回数はむしろ減っており、
1回だけのアップロードでは登録者数・再生回数獲得効果は小さいことが分かります。
批評者との比較
批評者と炎上と無関係なビジネス系YouTuberを比較し、
ビジネス系YouTuber全体の動きに対し、批評者の登録者数・再生回数が有意に増加しているかを確認しました。
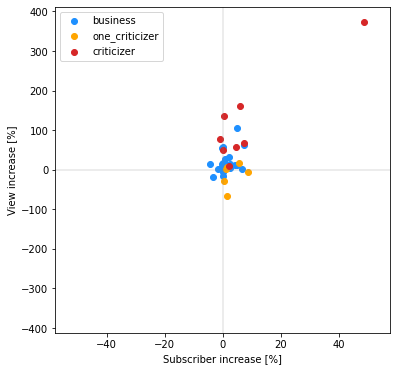
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
ax.scatter(subscriber_increase_list_business, view_increase_list_business,
c='dodgerblue', label='business')
ax.scatter(subscriber_increase_list_one, view_increase_list_one,
c='orange', label='one_criticizer')
ax.scatter(subscriber_increase_list, view_increase_list,
c='tab:red', label='criticizer')
ax.legend(loc='upper left')
ax.set_xlim(-xlim, xlim)
ax.set_ylim(-ylim, ylim)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
ax.set_xlabel('Subscriber increase [%]')
ax.set_ylabel('View increase [%]')
青色の炎上と無関係なビジネス系youTubeと比べ、赤色の批評者は右上にシフトしており、登録者数・再生回数共に増加していることが分かります。
これだけでは定性的なので、教師なし学習の一種であるマハラノビスタグチ法で、統計的な有意差を求めます。
(炎上と無関係なビジネス系YouTuberを正常データとして学習し、マハラノビス距離を求める)
from scipy.spatial import distance
X_criticizer = np.array([subscriber_increase_list, view_increase_list]).T # 批評者データ
X_normal = np.array([subscriber_increase_list_business, view_increase_list_business]).T # ビジネス系YouTuberを正常データとして利用
mean = np.mean(X_normal, axis=0) # 平均
cov = np.cov(X_normal.T) # 分散共分散行列
cov_i = np.linalg.pinv(cov) # 分散共分散逆行列
# マハラノビス距離
mahalanobis_dist = np.apply_along_axis(lambda x:
distance.mahalanobis(x, mean, cov_i), 1, X_criticizer)
mahalanobis_dist = pd.Series(mahalanobis_dist,
index=list(df_criticizer.groupby('transferred_name').groups.keys()))
print(mahalanobis_dist)
A 16.454616
B 4.715818
C 1.357254
D 2.527822
E 4.335887
F 0.579273
G 1.316450
H 2.086137
2変数のマハラノビス距離の二乗は自由度2のカイ二乗分布に従うという理論に基づくと、
有意水準0.05でマハラノビス距離>2.45なら有意差ありと判断できるので、
少なくともA, B, D, Eの批評者は、ビジネス系YouTuber全体に対して、炎上日を境に有意に登録者・再生回数を増加させていると判断できそうです。
インフルエンサー側の分析
次に、炎上したインフルエンサー側のチャンネル登録者数と再生回数の推移を分析します。
可視化とデータクレンジング
動画削除に起因したマイナスの補正を実施し、炎上前後の登録者数と再生回数を折れ線グラフで可視化します。
flaming_date = df[df['transferred_name']=='influencer']['flaming_date'][0].to_pydatetime()# 炎上日
# インフルエンサーのデータ読込
df_influencer = df[df['classification']=='influencer_main'].copy()
# 再生回数がマイナスのデータ&直後の異常データを補正
df_influencer = df_influencer.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週が100となるよう規格化
df_influencer = df_influencer.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, flaming_date))
n_channels = df_influencer['transferred_name'].nunique() # チャンネル数
# プロット用のaxes
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_influencer.groupby('transferred_name')):
# 正規化したチャンネル登録者数をプロット
plot_before_after(ax=axes[0], df_src=df_ch,
date_col='date', y_col='subscriber_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 正規化した再生数をプロット
plot_before_after(ax=axes[1], df_src=df_ch,
date_col='date', y_col='view_norm', flaming_date=flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
c=color_list[i], name=name)
# 図中に炎上日をプロット
axes[0].text(flaming_date, axes[0].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
axes[1].text(flaming_date, axes[1].get_ylim()[0],
f'Flaming date = {flaming_date.strftime("%Y/%m/%d")}', verticalalignment='bottom', horizontalalignment='left')
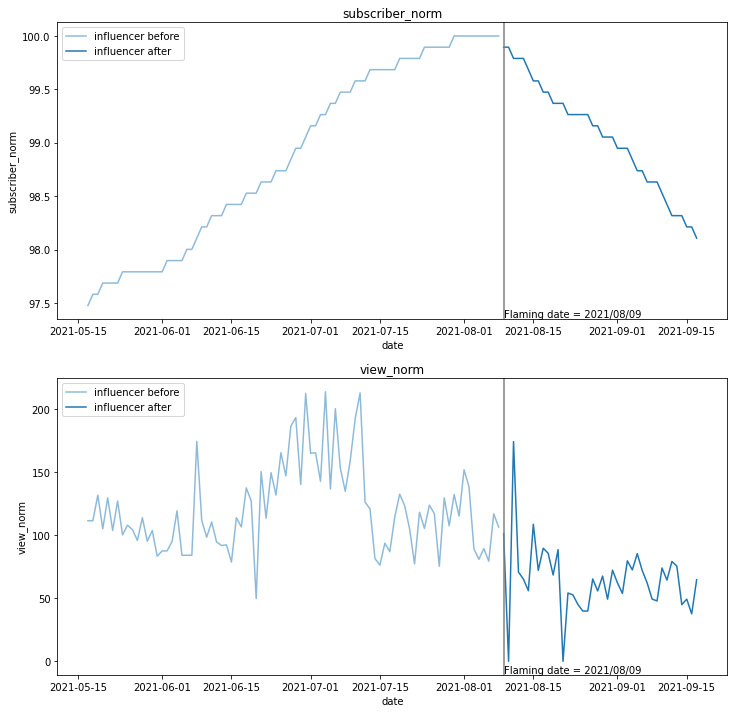
批評者のときとは逆に、登録者数(上のグラフ)・再生回数(下のグラフ)ともに炎上日(灰色の縦線)を境に減っているようように見えます。
本当に減っているのかどうか、定量的な評価を進めていきます
定量分析:時系列分析
批評者のときと同じ手法(ARIMAモデル)で、トレンドから推定される予測値と、炎上後の実測値との差分をとることで、トレンドを差し引いた炎上起因の増加率を算出します。
モデル作成と予測結果の可視化(登録者数)
インフルエンサーのチャンネル登録者数の、炎上後の予測値からの増加率を算出します
pred_subscribers_influencer = {} # 予測結果保持用
fig, axes = plt.subplots(1, 1, figsize=(8, 3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_influencer.groupby('transferred_name')):
pred_subscribers_influencer[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes,
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
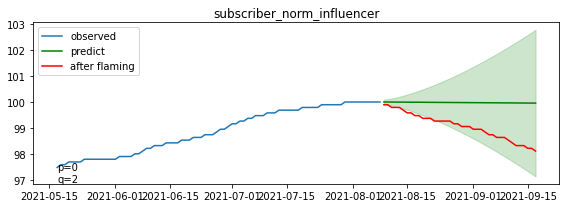
断続的に信頼区間を下回るレベルで、チャンネル登録者数が減少していることが分かります。
モデル作成と予測結果の可視化(再生回数)
インフルエンサーの再生回数の、炎上後の予測値からの増加率を算出します
pred_subscribers_influencer = {} # 予測結果保持用
fig, axes = plt.subplots(1, 1, figsize=(8, 3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_influencer.groupby('transferred_name')):
pred_subscribers_influencer[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes,
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
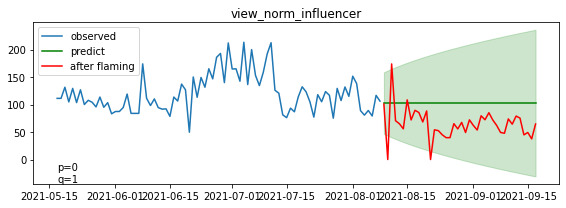
断続的に信頼区間を下回るレベルで、再生回数が減少していることが分かります。
予測値からの実測値増加率
批評者のときと同様に、横軸にチャンネル登録者数の増加率、縦軸に再生回数の増加率をとって散布図でプロットします。
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list_influencer = [] # 登録者数増加率格納用
view_increase_list_influencer = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_influencer.groupby('transferred_name')):
# 炎上前後39日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers_influencer[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views_influencer[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list_influencer.append(subscriber_increase_ratio)
view_increase_list_influencer.append(view_increase_ratio)
ax.set_xlim(-50, 50)
ax.set_ylim(-400, 400)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list_influencer)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list_influencer)}%')
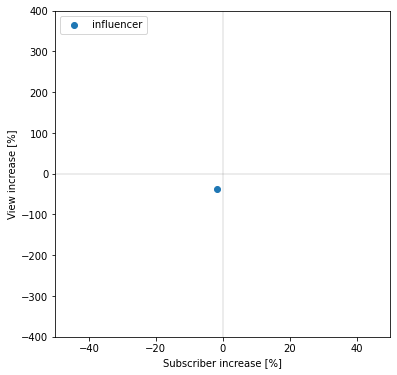
批評者のときとは逆に、登録者数、再生回数共に減少している(散布図上の第三象限にある)ことが分かります。
批評者との比較
先ほどの批評者での結果と重ねてプロットします。
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
ax.scatter(subscriber_increase_list, view_increase_list,
c='tab:red', label='criticizer')
ax.scatter(subscriber_increase_list_influencer, view_increase_list_influencer,
c='tab:blue', label='influencer_main')
ax.legend(loc='upper left')
ax.set_xlim(-50, 50)
ax.set_ylim(-400, 400)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
ax.set_xlabel('Subscriber increase [%]')
ax.set_ylabel('View increase [%]')
plt.show()
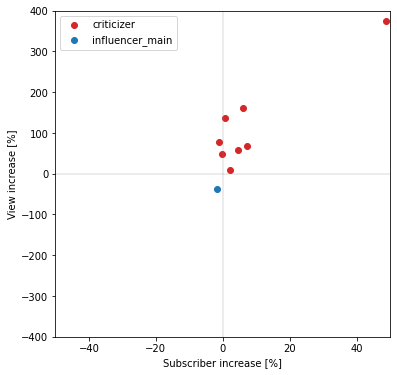
登録者数・再生回数共に、炎上したインフルエンサーは減少(第三象限)、批評者は増加(第一象限)する傾向にあり、対照的な結果となっていることが分かります。
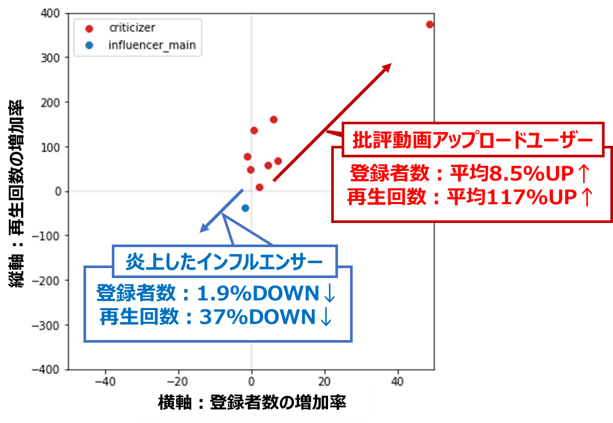
他のインフルエンサーの分析
メインの分析対象としたインフルエンサー以外の炎上事例でも、同様の傾向が見られるかを分析しました。
分析対象のチャンネルは以下となります。
・直近1年以内(2020/9~2021/9)に炎上を経験したビジネス系YouTuber4名
・2021年6月に同一の不祥事を経験したYouTuber19名(ビジネス系以外)
直近1年以内に炎上を経験したビジネス系YouTuber
df_other = df[df['classification']=='influencer_other'].copy()
# 再生回数がマイナスのデータ&直後の異常データを補正
df_other = df_other.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週が100となるよう規格化
df_other = df_other.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, group['flaming_date'].iat[0].to_pydatetime()))
n_channels = df_other['transferred_name'].nunique() # チャンネル数
# 登録者数の予測
pred_subscribers_other = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_other.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
pred_subscribers_other[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 再生回数の予測
pred_views_other = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_other.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
pred_views_other[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='view_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_VIEW, p_max=P_MAX_VIEW, q_max=Q_MAX_VIEW, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 登録者数と再生回数の予測値からの増加率
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list_other = [] # 登録者数増加率格納用
view_increase_list_other = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_other.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers_other[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views_other[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list_other.append(subscriber_increase_ratio)
view_increase_list_other.append(view_increase_ratio)
ax.set_xlim(-50, 50)
ax.set_ylim(-400, 400)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list_other)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list_other)}%')
チャンネル登録者数増加率平均=-7.703265221667188%
再生回数数増加率平均=-29.786313035196347%
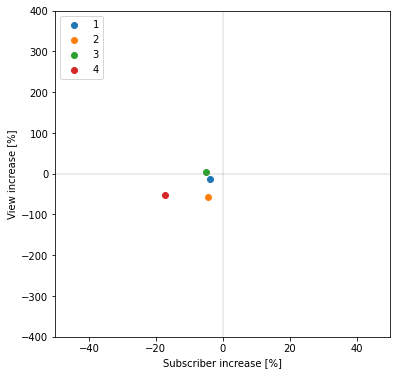
メイン分析対象のインフルエンサーと同様に、登録者数、再生回数共に減少している(散布図上の第三象限にある)ことが分かります。
同一の不祥事を経験したビジネス系以外のYouTuber19名
df_drunk = df[df['classification']=='influencer_drunk'].copy()
# 再生回数がマイナスのデータ&直後の異常データを補正
df_drunk = df_drunk.groupby('transferred_name').apply(
lambda group: modify_minus_view(group, 'view_count', 'date'))
# 炎上前週が100となるよう規格化
df_drunk = df_drunk.groupby('transferred_name').apply(
lambda group: normalize_last_week(group, group['flaming_date'].iat[0].to_pydatetime()))
n_channels = df_drunk['transferred_name'].nunique() # チャンネル数
# 登録者数の予測
pred_subscribers_drunk = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_drunk.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
pred_subscribers_drunk[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='subscriber_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_SUBSCRIBER, p_max=P_MAX_SUBSCRIBER, q_max=Q_MAX_SUBSCRIBER, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 再生回数の予測
pred_views_drunk = {} # 予測結果保持用
fig, axes = plt.subplots(n_channels, 1, figsize=(8, n_channels*3)) # プロット用のaxes
for i, (name, df_ch) in enumerate(df_drunk.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
pred_views_drunk[name] = compare_pred_and_flaming(df_src=df_ch, date_col='date', y_col='view_norm', ax=axes[i],
flaming_date=flaming_date, before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING,
d=D_VIEW, p_max=P_MAX_VIEW, q_max=Q_MAX_VIEW, alpha=ALPHA)
plt.tight_layout()
plt.show()
# 登録者数と再生回数の予測値からの増加率
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
subscriber_increase_list_drunk = [] # 登録者数増加率格納用
view_increase_list_drunk = [] # 再生回数増加率格納用
# チャンネルごとにループ
for i, (name, df_ch) in enumerate(df_drunk.groupby('transferred_name')):
flaming_date = df_ch['flaming_date'].iat[0].to_pydatetime() # 炎上日
# 炎上前後40日ずつを抜き出し
df_before, df_after = devide_before_after(df_ch, 'date', flaming_date,
before_period=BEFORE_FLAMING, after_period=AFTER_FLAMING)
# 炎上後の予測値に対する増加率を散布図プロット
subscriber_increase_ratio, view_increase_ratio \
= plot_increase_scatter(x_before=pred_subscribers_drunk[name].iloc[-1], x_after=df_after['subscriber_norm'].iloc[-1],
y_before=pred_views_drunk[name].mean(), y_after=df_after['view_norm'].mean(), label=name, ax=ax)
subscriber_increase_list_drunk.append(subscriber_increase_ratio)
view_increase_list_drunk.append(view_increase_ratio)
ax.set_xlim(-50, 50)
ax.set_ylim(-400, 400)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
print(f'チャンネル登録者数増加率平均={np.mean(subscriber_increase_list_drunk)}%')
print(f'再生回数数増加率平均={np.mean(view_increase_list_drunk)}%')
チャンネル登録者数増加率平均=-3.3589465205467555%
再生回数数増加率平均=12.995516075001039%
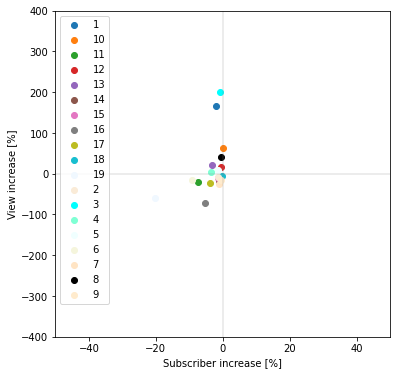
チャンネル登録者数は、ほぼ全て(19チャンネル中18チャンネル)のチャンネルで減少していました。
再生回数は平均が増加していますが、大きく再生回数を伸ばした以下の2チャンネルに引っ張られて増加しています。
(この2チャンネルを除けば平均で7%の再生回数減少)
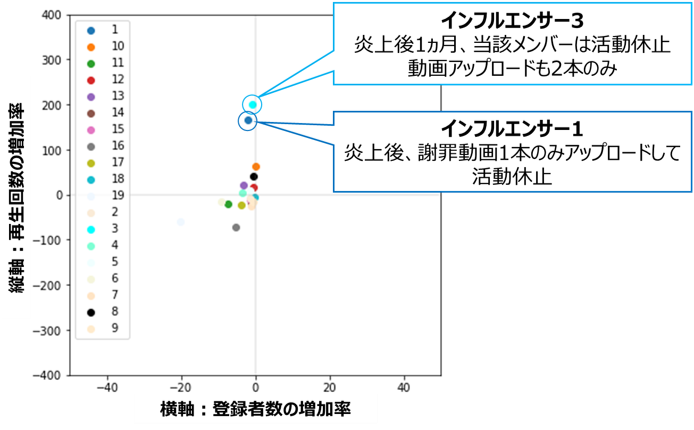
この2チャンネル(インフルエンサー1および3)の炎上後の動向を調べたところ、
| チャンネル | 炎上後の動向 |
|---|---|
| インフルエンサー1 | 謝罪動画を1本アップしたのち、活動休止(2021/9現在も休止中) |
| インフルエンサー3 | 謝罪動画をアップしたのち、当該メンバーは活動休止。残った1人で活動するも投稿ペースは通常の1/3程度まで低下(その後チャンネルとしても活動休止を発表) |
どちらも謝罪動画を1本上げた後はしばらく活動休止状態となっており、
活動をしないことで再生回数が大きく伸びるという、一見矛盾した結果となっています。
私見ですが、休止状態に入る事で、世間から「反省してみそぎに入った」と認識され、好感が得られたのかもしれません。
この結果は、「炎上したらどのように対処するのが正解か?」に対するヒントとなりそうです。
全炎上インフルエンサーの比較
本節で分析した全てのインフルエンサーの結果を重ねてプロットします
fig, ax = plt.subplots(1, 1, figsize=(6, 6)) # プロット用のaxes
ax.scatter(subscriber_increase_list_drunk, view_increase_list_drunk,
c='tab:purple', label='influencer_drunk')
ax.scatter(subscriber_increase_list_other, view_increase_list_other,
c='tab:green', label='influencer_other')
ax.scatter(subscriber_increase_list_influencer, view_increase_list_influencer,
c='tab:blue', label='influencer_main')
ax.legend(loc='upper left')
ax.set_xlim(-50, 50)
ax.set_ylim(-400, 400)
ax.axvline(x=0, color='gray', alpha=0.2)
ax.axhline(y=0, color='gray', alpha=0.2)
ax.set_xlabel('Subscriber increase [%]')
ax.set_ylabel('View increase [%]')
plt.show()
subscriber_increase_list_all = subscriber_increase_list_influencer + subscriber_increase_list_other + subscriber_increase_list_drunk
view_increase_list_all = view_increase_list_influencer + view_increase_list_other + view_increase_list_drunk
print(f'登録者減少チャンネル数={len([v for v in subscriber_increase_list_all if v <= 0])}/{len(subscriber_increase_list_all)}')
print(f'再生回数減少チャンネル数={len([v for v in view_increase_list_all if v <= 0])}/{len(view_increase_list_all)}')
登録者減少チャンネル数=23/24
再生回数減少チャンネル数=15/24
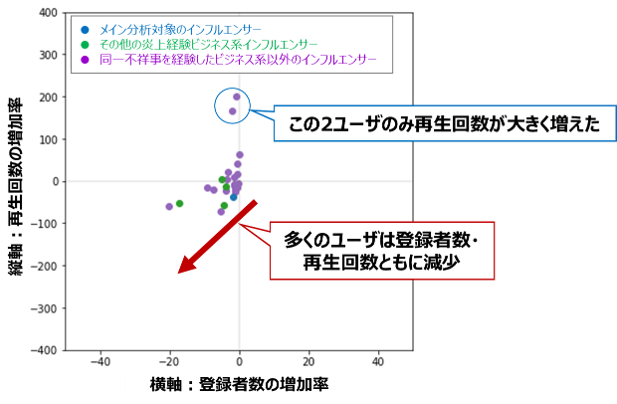
多くのチャンネルで登録者数・再生回数共に落としており、炎上が視聴者の獲得にマイナスの影響を与えていることが分かります。
(特にビジネス系インフルエンサーは1例を除き全て登録者数・再生回数が減少)
まとめ
炎上後40日間の登録者数・再生回数を分析した結果、以下のような知見が得られました。
1. 登録者数・再生回数共に、炎上したインフルエンサーは減少、炎上参加者(批評者)は増加する
2. 炎上参加者は、炎上関係の批評動画アップロード数が多いほど、登録者数・再生回数が増加する
3. 複数の事例を分析しても、基本的に炎上したインフルエンサーは登録者数・再生回数共に落ちている
4. 炎上で再生回数が大きく増えたインフルエンサーは、炎上後に休止状態に入っていた
結論
炎上が起こる原因として、「社会正義に対する義憤」(正の感情)、「成功者への嫉妬心」(負の感情)という、感情的な側面が挙げられることが多いです。
これらに加え本分析の結果、
「炎上参加による視聴者・登録者の獲得」
という経済的なメリットが明確に確認できました。
これは、YouTubeが主要な発信ツールとして認知された2021年においては
「炎上に対して完璧な対応をし、感情面での批判意図を完全に消すことができたとしても、なお批判するメリットが残る」
ことを意味しており、一度炎上状態に陥ると消火が困難であることが伺えます。
また、「炎上商法」という言葉がありますが、データを見ると基本的に炎上したインフルエンサーは登録者数・再生回数を落としており、数字上はリスクに見合わない戦術だと判断するのが適切です。
炎上にワクワクしてしまう性格の持ち主でもない限り、炎上するような発言・行動は避けることが、発信者の心得として重要だと結論づけられそうです。
おわりに
こんな分析結果を出しておいてなんですが、行き過ぎた批判はインフルエンサー本人・および周囲の人に過剰な精神的負担をかける可能性が高いので、むやみな炎上への便乗は控えて頂ければと思います。