いきさつ
機密データの匿名加工に関する案件を受けたのでPoCしたいということでどのように進めるか考えていたのですが、話の中で「形態素解析で自由記述欄にある個人情報を全て拾ってほしい(漏れなし)」というように言われました。当然、形態素解析で100%の結果を保証することは不可能です。1その辺の認識をすり合わせていく中でさらにトンデモ発言が出てきました。
「全数調査!?やりたくない!これ(対象データの一部)だけで20GBあるし」
「適当にサンプリングしてその中にエラーがなければ100%とみなせばいいよ」
耳を疑ったのですがぐっとこらえていかに間違っているか説得することにしました。そしてどのように上司やクライアントに全数調査が絶望的なスケールのデータにおいてミスがないことを説明するかを考えることになりました。
課題
当然全数調査は不可能です。例えば20GBの日本語テキストデータは凡そ71.6億文字2にもなります。小節1冊が約10万文字であることを考えると小節7万冊以上分のテキストデータということになり、これではプロジェクト期間内どころか一生かかっても調査を終えることができません。サンプリングは不可欠です。ここで検討するべき課題は2つ。
・サンプルサイズをどの程度にするのか
・標本集団から得られた結果をどう解釈し上司やクライアントを納得させるか
とりあえず「漏れありませんでした!」と報告するのはやめて「95%信頼区間で〇件から△件の漏れがあることが分かりました。」と報告するべきなのでどの手法を使って検定をしようか検討を始めました。
Waldの信頼区間の問題点
まぁ私は統計検定2級も取りましたし「これ統計検定でやったやつですわ楽勝~」と思い検討していたのですが重大な問題が発生することが分かりました。まずはWaldの検定を思い出しましょう。
Wald統計量:
$$
W = \frac{(\hat{p} - p_0)^2}{\text{SE}(\hat{p})^2}
$$
ここで、
$\hat{p}$: パラメータの最尤推定量
$p_0$: 帰無仮説で想定されるパラメータの値
$\text{SE}(\hat{p})$: $\hat{p}$の標準誤差
です。
信頼区間は
$$
\hat{p} \pm z_{\alpha/2} \cdot \text{SE}(\hat{p})
$$
となります。
サンプル中で加工漏れが1件も観測されなかった場合、最尤推定量は$\hat{p} = 0$となり、標準誤差は
$$
\text{SE}(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 0
$$
となります。$\text{SE}(\hat{p})$が0であった場合、Wald統計量は計算不能(不定形または発散)となり、信頼区間は[0, 0]となります。 こんなに意味のない結果はありません。困ります。
さらに、検定の論理にも矛盾があります。仮に$H_0: p = 0$という帰無仮説を設定できたとしても、これを棄却すると『$p \neq 0$』つまりミスがあることを示してしまい、望む結論と逆になります。$H_0: p \neq 0$のような帰無仮説は統計的検定の枠組みでは設定できません。3
加えて調べていく中でWaldの方法の前提条件を満たしていないことにも気づきました。そもそもこれは中心極限定理を根拠に標本比率の分布が正規分布に近似されることを前提にしていますが、今回はpが非常に0に近いため正規分布に近似できません。
まとめるとミスがないということを統計的に示すことはできず、Wald以外の方法で信頼区間を求めるほかにないということです。
新たな手法の探索
求めるべきは別の信頼区間を求める方法ということになりましたが、あいにく自分はWald法以外知らなかったので調べることにしました。Claudeによると Clopper-Pearson法(正確法) というものがあるようです。
特徴としては
・正規近似を使わない
・サンプルサイズが小さくても大きくても正確
・2項分布そのものを使った厳密な計算
というものがあげられるようです。
加えて今回は保守的な結果が求められる環境であることが予測されていたので、信頼区間が広めに出るというデメリットもそこまで悪いものではありませんでした。なのでコードを作って色々計算させたんですが信頼区間の下限が観測値を下回ることがありました。サンプリングされたものの中にミスが1件確認されたのに信頼区間に0が含まれているという状態です。「1件見つかってるのに信頼区間に0件が含まれてるのは論理的におかしいだろ!こんなの使えるか!」と別の手法を探すことになりました。結局これは表示する桁数の問題で実際には妥当な値だった4のですが当時は気づかず、Clopper-Pearson法のダメな点を探しに行き始めてしまいました。
調べているうちにこの論文に出会いました。
この論文は簡単に言うといろんな信頼区間の求め方あるけどそれぞれの特徴調べたよという論文です。
取り上げられていたのは
・Standard Interbal(Waldの信頼区間)
・Wilson Interbal
・Agresti-Coull Interbal
・Jeffreys Interbal
の4つでした。これらについて今回関係ある範囲でどのように説明されていたかをまとめます。
ちなみにこの論文で
"The Clopper–Pearson interval guarantees that the actual coverage probability is always equal to or above the nominal confidence level. However, for any fixed p, the actual coverage probability can be much larger than 1−α unless n is quite large, and thus the confidence interval is rather inaccurate in this sense."
Clopper–Pearson信頼区間は、実際の被覆確率が常に公称信頼水準と等しいか、それ以上であることを保証している。しかし、任意の固定されたpに対して、nがかなり大きくない限り、実際の被覆確率は1-αよりはるかに大きくなる可能性があり、したがってこの信頼区間はこの意味でかなり不正確である。
"The Clopper–Pearson interval is wastefully conservative and is not a good choice for practical use, unless strict adherence to the prescription Cp(n) ≥ 1−α is demanded."
「Cp(n)≧1-αの厳格な遵守が要求されない限り、Clopper–Pearson信頼区間は無駄に保守的であり、実用には適していない。
といったようにClopper–Pearson法は批判されていたので結果的には正しい突っ走りでした。
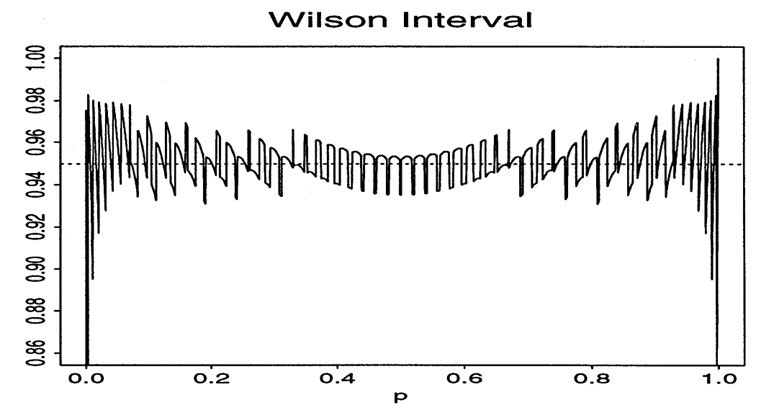
Standard Interbal(Waldの信頼区間)
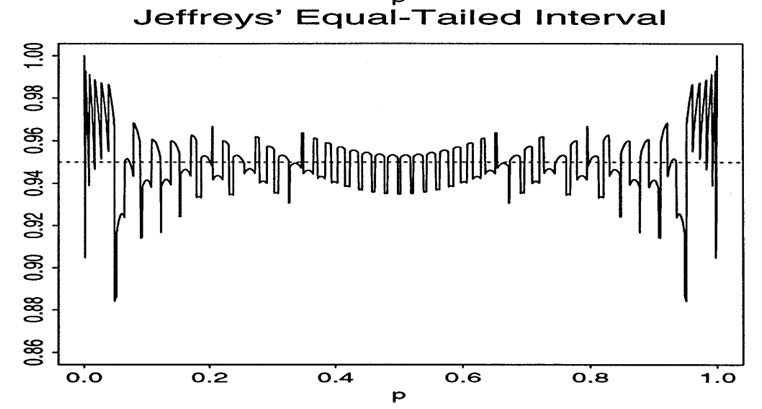
先のセクションである程度話したのでここでは被覆確率についてだけ見ます。語る上で重要な図を論文から引用します。
この図は横軸がp(尤度)で縦軸が被覆確率です。被覆確率とは信頼区間に真の値が含まれている確率のことで、例えば95%信頼区間を求めたのであれば95に近ければ近いほど良いです。被覆確率が小さい場合、信頼区間外に真の値がある確率が高くなり、被覆確率が高い場合過剰に保守的で結論の情報量が減ります。
Waldの信頼区間は左上の図で$p=0.5$付近ならば実用的なんですが$p=0$や$p=1$付近では下に振り切れてしまっています。今回は$p=0$付近であることが予測されるので採用できません。
余談ですが論文を丸ごと投げてWaldをボロカスに言っているところを教えてくださいとClaudeに聞いたところ引くくらい出てきて爆笑しました。

私はここが一番好きです。
Interval estimation of a binomial proportion is a very basic problem in practical statistics. The standard Wald interval is in nearly universal use. We first show that the performance of this standard interval is persistently chaotic and unacceptably poor. Indeed its coverage properties defy conventional wisdom. The performance is so erratic and the qualifications given in the influential texts are so defective that the standard interval should not be used.
二項比率の区間推定は実用統計学における非常に基本的な問題である。標準的なWald区間はおおよそ普遍的に使用されている。我々はまず、この標準区間の性能が持続的に混沌としており、受け入れがたく貧弱であることを示す。実際、その被覆特性は従来の常識に反している。パフォーマンスは極めて不規則であり、影響力のある教科書で与えられている推奨条件は非常に欠陥があるため、標準区間は使用されるべきではない。
論文でここまでボロカスに書くことあるんだ……
Wilson Interbal
Wisonの信頼区間についてまずは簡単に見てみます。Wilson信頼区間は、スコア検定(score test)に基づく信頼区間で、Waldの信頼区間の問題点を改善した手法です。
公式
$$
\frac{\hat{p} + \frac{z_{\alpha/2}^2}{2n} \pm z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z_{\alpha/2}^2}{4n^2}}}{1 + \frac{z_{\alpha/2}^2}{n}}
$$
ここで
$\hat{p}$: 観測された標本比率
$n$: サンプルサイズ
$z_{\alpha/2}$: 標準正規分布の上側$\alpha/2$点
です。
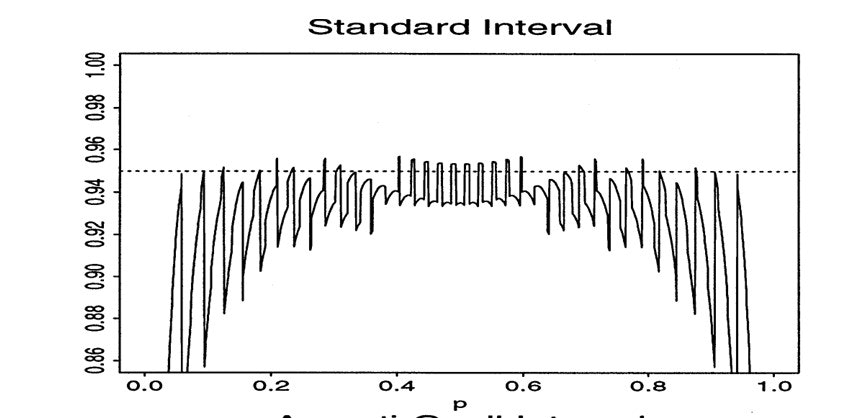
この信頼区間はWaldと違って$p=0$や$p=1$付近のような境界値付近でも適切に機能し被覆確率が安定します。さっきの図では右上図がWilsonのものですがWaldよりは高い被覆確率を広い範囲で維持できていることが分かります。実際、よく使われる信頼区間であり論文のAbstractでも使用を推奨しています。
Based on this analysis, we recommend the Wilson interval or the equal-tailed Jeffreys prior interval for small n and the interval suggested in Agresti and Coull for larger n.
この分析から、我々は小さなnに対してはWilson信頼区間あるいはJeffreys事前分布による等裾信頼区間を、大きなnについてはAgresti-coull信頼区間を用いることを推奨する。と書かれています。
しかし今回は$p=0$付近での使用なので少し心許ないです。境界値付近での振動がかなり大きいのであまり適していません。もちろんこれは$n=50$の場合なので今回のスケールだと振動の幅は小さくなることが予測されますがそれを考慮しても大きいですね。
Agresti-Coull Interbal
次にAgresti-Coullの信頼区間についても見てみます。Agresti-Coull信頼区間は、Waldの信頼区間に簡単な修正を加えることで性能を大幅に改善した手法です。調整Wald法という別名からもわかるように、観測データに成功2回と失敗2回を追加するという補正を行ってWaldの信頼区間を適用する方法です。
$$
\tilde{n} = n + 4
$$
$$
\tilde{p} = \frac{x + 2}{n + 4}
$$
のように補正をかけた後に
$$
\tilde{p} \pm z_{\alpha/2} \cdot \sqrt{\frac{\tilde{p}(1-\tilde{p})}{\tilde{n}}}
$$
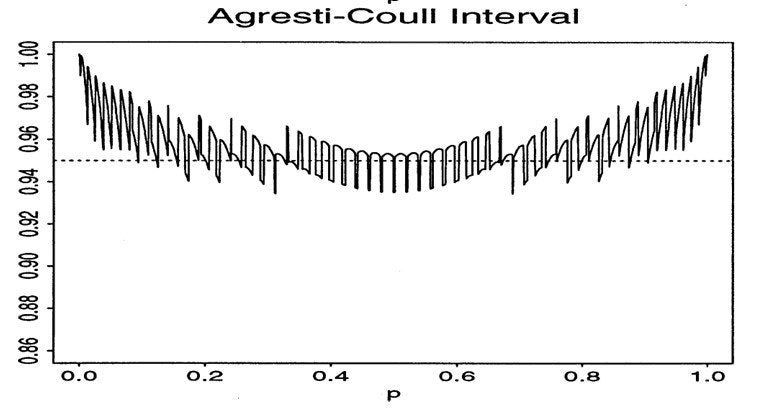
Waldと同様に実装が楽です。補正の影響で標準誤差が0になることを防いでいるので安定した結果が得られるようになっています。先ほど引用した部分にもあったように大きいサンプルサイズに対して用いる分には被覆確率の振動も少なくかなりいい結果をもたらしますが、総じて保守的な結果になることには注意が必要です。また、補正値が固定の量なのでこの2という補正値が相対的に大きくなる場面(サンプルサイズが小さい場面)においては実体と乖離した結果が出てくると思われるので使用しない方がいいと思います。また境界値付近ではかなり保守的な結果が得られる($p=0$付近で被覆確率が1.0にかなり近い)ため今回の用途には合いませんでした。特にこれは$n=50$の場合でもこの振動の小ささなのでサンプルサイズを大きくしても改善の余地が少ないのもマイナス要素でした。
Jeffreys Interbal
Jeffreys信頼区間は、ベイズ統計に基づく信頼区間で、Jeffreys事前分布を用いて計算されます。先に挙げた手法(頻度論的な手法)とは異なるアプローチを取ります。
事前分布
$$
p(p) = \text{Beta}\left(\frac{1}{2}, \frac{1}{2}\right)
$$
事後分布
観測データ(成功$x$回、試行$n$回)から得られる事後分布
$$
p \mid x \sim \text{Beta}\left(x + \frac{1}{2}, n - x + \frac{1}{2}\right)
$$
信頼区間
95%等裾信頼区間は、この事後分布の2.5パーセンタイルと97.5パーセンタイルで定義される
$$
\left[ F_{\text{Beta}(x+1/2, n-x+1/2)}^{-1}(0.025), F_{\text{Beta}(x+1/2, n-x+1/2)}^{-1}(0.975) \right]
$$
ベイズ統計とは
ベイズ統計は、パラメータを確率変数として扱い、観測データから事後分布を計算する統計手法です。頻度論的統計とは根本的に異なるアプローチを取ります。
$$
p(\theta \mid \text{data}) = \frac{p(\text{data} \mid \theta) \cdot p(\theta)}{p(\text{data})}
$$
$p(\theta)$: 事前分布(prior)
$p(\text{data} \mid \theta)$: 尤度(likelihood)
$p(\theta \mid \text{data})$: 事後分布(posterior)
事前分布(何かしらの想定確率など)を尤度(今得られた結果)でアップデートして事後確率(更新された想定確率)を求めていく手法です。信頼区間の解釈が頻度論の場合と異なり、「真値が95%の確率でこの区間にある」という結論になります。 ベイズ統計を行う際は事前分布が恣意的なものになっていないか注意する必要があります。
(追記): 厳密には「信頼区間」は頻度論の用語で、ベイズでは「信用区間」または「確信区間」と呼びます。ただし実務では混同されることも多いです。あとで知ったのでこの記事ではすべて信頼区間と書いています。
Jeffreys信頼区間では事前分布を$\text{Beta}\left(\frac{1}{2}, \frac{1}{2}\right)$としています。これは無情報事前分布と呼ばれ、特定の値に偏らない客観的な分布です。計算は複雑(手計算不可能)ですが、$p=0$付近で被覆確率が大きく落ちていないこと、今回調べた手法の中では0.95から大きく外れてない方であること5、ベイズ統計由来であるために得られる結論も直感的であることから今回はJeffreys信頼区間を採用することにしました。サンプルサイズが大きくなるとさらに振動の幅も小さくなることが予想されるのでそういった面でもよろしいです。
実装
上司やクライアントにこれ以上の説明はできる気がしないので解決したことにします。次にサンプルサイズをどうやって決めるかについて考えます。これは一人では結論が出ない問題なので会議の場で決まることになることが予想されます。目の前でいろんな値を試してみてよさそうな数値が出たときに「まぁこの数なら大丈夫じゃない?」と言わせれば勝ちです。したがって対話式で母集団サイズとサンプルサイズとサンプル内検出数を入力させて現実的な判断をしてもらおうと思います。
import numpy as np
from scipy import stats
def jeffreys_ci(x, n, alpha=0.05):
"""
Jeffreys prior equal-tailed confidence interval
Reference
---------
Brown, L. D., Cai, T. T., & DasGupta, A. (2001).
Interval Estimation for a Binomial Proportion.
Statistical Science, 16(2), 101-133.
Parameters
----------
x : int
成功数(検出数)
n : int
試行回数(サンプルサイズ)
alpha : float
有意水準(デフォルト0.05で95%信頼区間)
Returns
-------
tuple : (lower, upper)
信頼区間の下限と上限
"""
if n == 0:
return (0.0, 0.0)
if x == 0:
lower = 0.0
upper = stats.beta.ppf(1 - alpha/2, x + 0.5, n - x + 0.5)
elif x == n:
lower = stats.beta.ppf(alpha/2, x + 0.5, n - x + 0.5)
upper = 1.0
else:
lower = stats.beta.ppf(alpha/2, x + 0.5, n - x + 0.5)
upper = stats.beta.ppf(1 - alpha/2, x + 0.5, n - x + 0.5)
return (lower, upper)
def calculate_population_estimate(N, n, x):
"""
母集団における推定値と信頼区間を計算(95%と99%の両方)
Parameters
----------
N : int
母集団サイズ
n : int
サンプルサイズ
x : int
サンプル内検出数
Returns
-------
dict : 計算結果の辞書
"""
sample_rate = x / n if n > 0 else 0
sampling_fraction = n / N if N > 0 else 0
# 95%信頼区間
lower_rate_95, upper_rate_95 = jeffreys_ci(x, n, alpha=0.05)
# 99%信頼区間
lower_rate_99, upper_rate_99 = jeffreys_ci(x, n, alpha=0.01)
return {
'sample_rate': sample_rate,
'sample_rate_percent': sample_rate * 100,
'sampling_fraction': sampling_fraction,
# 95%信頼区間
'ci_95_lower_percent': lower_rate_95 * 100,
'ci_95_upper_percent': upper_rate_95 * 100,
'ci_95_lower_count': N * lower_rate_95,
'ci_95_upper_count': N * upper_rate_95,
# 99%信頼区間
'ci_99_lower_percent': lower_rate_99 * 100,
'ci_99_upper_percent': upper_rate_99 * 100,
'ci_99_lower_count': N * lower_rate_99,
'ci_99_upper_count': N * upper_rate_99,
}
def print_results(results, N, n, x):
"""
結果を表示
"""
print("\n" + "="*70)
print("統計分析結果(Jeffreys法)")
print("="*70)
print(f"\n[入力データ]")
print(f" 母集団サイズ (N): {N:,}")
print(f" サンプルサイズ (n): {n:,}")
print(f" サンプル内検出数 (x): {x:,}")
print(f" 抽出率: {results['sampling_fraction']*100:.2f}%")
# 抽出率による警告
if results['sampling_fraction'] >= 0.10:
print(f"\n[警告] 抽出率が{results['sampling_fraction']*100:.1f}%と高いため、")
print(f" 有限母集団補正(FPC)を考慮すべき可能性があります。")
print(f" この信頼区間は若干保守的(広め)になっている可能性があります。")
elif results['sampling_fraction'] >= 0.05:
print(f"\n[注意] 抽出率が{results['sampling_fraction']*100:.2f}%です。")
print(f" 一般に5%を超えると有限母集団補正の効果が無視できなくなります。")
print(f"\n[サンプル内の観測値]")
print(f" 検出率: {results['sample_rate_percent']:.6f}% ({x}/{n})")
print(f"\n[95%信頼区間]")
print(f" 割合:")
print(f" 下限: {results['ci_95_lower_percent']:.6f}%")
print(f" 上限: {results['ci_95_upper_percent']:.6f}%")
print(f" 母集団件数:")
print(f" 下限: {results['ci_95_lower_count']:,.1f} 件")
print(f" 上限: {results['ci_95_upper_count']:,.1f} 件")
print(f"\n[99%信頼区間]")
print(f" 割合:")
print(f" 下限: {results['ci_99_lower_percent']:.6f}%")
print(f" 上限: {results['ci_99_upper_percent']:.6f}%")
print(f" 母集団件数:")
print(f" 下限: {results['ci_99_lower_count']:,.1f} 件")
print(f" 上限: {results['ci_99_upper_count']:,.1f} 件")
print("\n" + "="*70)
def get_positive_integer(prompt, allow_zero=False):
"""
正の整数を入力させる
"""
while True:
try:
value = int(input(prompt))
if value < 0 or (not allow_zero and value == 0):
print(" 正の整数を入力してください")
continue
return value
except ValueError:
print(" 有効な整数を入力してください")
def validate_inputs(N, n, x):
"""
入力値の妥当性をチェック
"""
errors = []
if n > N:
errors.append(f"サンプルサイズ({n})が母集団サイズ({N})を超えています")
if x > n:
errors.append(f"検出数({x})がサンプルサイズ({n})を超えています")
return errors
def main():
"""
メインプログラム
"""
print("="*70)
print("二項分布信頼区間計算ツール(Jeffreys法)")
print("="*70)
while True:
N = get_positive_integer("\n母集団サイズ (N): ")
n = get_positive_integer("サンプルサイズ (n): ")
x = get_positive_integer("サンプル内検出数 (x): ", allow_zero=True)
errors = validate_inputs(N, n, x)
if errors:
print("\n入力エラー:")
for error in errors:
print(f" - {error}")
print("\n再度入力してください。")
continue
break
results = calculate_population_estimate(N, n, x)
print_results(results, N, n, x)
if __name__ == "__main__":
main()
面倒だったのでほとんどClaudeに書かせましたが色々突っ込みを入れたのでまぁ妥当なものかと思います。
このコードにはFPCという解説していないものが出てきました。解説します。
FPC(有限母集団補正)
有限母集団補正(FPC: Finite Population Correction)
これまで説明してきた信頼区間の公式は、すべて無限母集団または復元抽出を前提としています。しかし実際のサンプリングでは
・母集団サイズ$N$が有限
・非復元抽出(同じ要素を2回選ばない)
という状況が多くあります。このとき、標準誤差を補正する必要があります。
FPC係数
有限母集団から非復元抽出する場合、標準誤差に以下の係数を掛けます
$$
\text{FPC} = \sqrt{\frac{N - n}{N - 1}}
$$
ここでは
$N$: 母集団サイズ
$n$: サンプルサイズ
FPCの効果
・$n \ll N$(サンプルが母集団に比べて十分小さい)のとき: $\text{FPC} \approx 1$(ほぼ影響なし)
・$n$が$N$に近づくと: $\text{FPC} < 1$(標準誤差が小さくなる)
・$n$ = $N$(全数調査)のとき: $\text{FPC} = 0$(誤差なし)
いつFPCが重要か
一般的な目安だと
・$\frac{n}{N} < 0.05$(抽出率5%未満): FPCはほぼ無視できる
・$\frac{n}{N} \geq 0.05$: FPCを適用すべき
とされているようです。これは慣例的な話で場面場面で許容できる誤差を検討する必要があります。
(cf.)抽出率とFPC係数の関係
| 抽出率 | FPC係数 | 標準誤差の減少 |
|---|---|---|
| 1% | 0.995 | 0.5% |
| 5% | 0.975 | 2.5% |
| 10% | 0.949 | 5.1% |
| 20% | 0.894 | 10.6% |
| 50% | 0.707 | 29.3% |
この標準誤差のズレをどこまで許容できるかという話です。
例えばWilson信頼区間に適用してみます。
$$
\frac{\hat{p} + \frac{z^2}{2n} \pm z\sqrt{\frac{\hat{p}(1-\hat{p})}{n} \cdot \frac{N-n}{N-1} + \frac{z^2}{4n^2}}}{1 + \frac{z^2}{n}}
$$
こんな感じに使えばいいわけです。
しかし、今回採用したのはJeffreys信頼区間なのでFPCの適用は複雑です。FPCは頻度論的な標準誤差の補正法なのでベイズ統計に持ち込むと理論が崩壊します。頑張ればできるらしいんですがClaude曰く「超幾何分布ベースのベイズモデルを構築する必要があり、非常に複雑です。頻度論的な近似として、尤度にFPCを組み込むことも可能ですが、一般的ではありません。」と言っているのであきらめて警告を出すにとどめました。そもそもFPC考慮しないといけないくらいの量をサンプリングしたくない!
実行結果
実行するとこんな感じになります。
======================================================================
二項分布信頼区間計算ツール(Jeffreys法)
======================================================================
母集団サイズ (N): 10000
サンプルサイズ (n): 2000
サンプル内検出数 (x): 5
======================================================================
統計分析結果(Jeffreys法)
======================================================================
[入力データ]
母集団サイズ (N): 10,000
サンプルサイズ (n): 2,000
サンプル内検出数 (x): 5
抽出率: 20.00%
[警告] 抽出率が20.0%と高いため、
有限母集団補正(FPC)を考慮すべき可能性があります。
この信頼区間は若干保守的(広め)になっている可能性があります。
[サンプル内の観測値]
検出率: 0.250000% (5/2000)
[95%信頼区間]
割合:
下限: 0.095456%
上限: 0.547117%
母集団件数:
下限: 9.5 件
上限: 54.7 件
[99%信頼区間]
割合:
下限: 0.065133%
上限: 0.667438%
母集団件数:
下限: 6.5 件
上限: 66.7 件
======================================================================
まとめ
今回は全数調査が絶望的なスケールのデータにおいてミスがないことを示したいと思い結構頑張りました。現時点で自分が書いた記事の中では最も高度な内容になっているかと思います。結果として当然ミス0を示すことはできないのですがいい感じの落としどころを見つけられたかなと思います。この調査の中で初めて真面目に英語で書かれた数学の論文を読みに行きましたしベイズ統計とも結構仲良くなれた感触が得られました。
正解が一つではない(あるかもわからない)課題に対して課題を設定し、現れた障壁を高度な専門知識を以て最適解を探し、理論を理解したうえでPythonで実装する経験を積めたので満足です。
-
全数調査をすればその結果に対しては100%を担保できるがそんなことをして意味がある場面はかなり限られる。精度結果の100%を保障することは理論的に可能だが、形態素解析器の精度100%を保障することは不可能。 ↩
-
日本語文字はUTF-8の場合3バイトを使う。実際には英数字記号も含まれるので文字数はもっと多くなると思われる。 ↩
-
$p \neq 0$のような帰無仮説は検定統計量の分布を特定できないため統計的検定の枠組みでは設定できない。 ↩
-
例えば50万件中3000件をサンプリングしてミスが1件確認された場合、Clopper-Pearson法による95%信頼区間の下限は約0.000008と、極めて0に近い値になる。これは1/500000を上回っており、当然に論理的に否定できる部分はない。この0.000008が0と表示されたので焦ったわけです。 ↩
-
いや振動の中心は0.97くらいじゃんと突っ込まれそうなのですが、今回は保守的な結果を出すことがそこまで悪いことではないため目を瞑ることにしました。 ↩