はじめに
この記事は,一応「Deep Learning論文紹介 Advent Calendar 2019」の12/20に投稿する予定だったものですが,ずれにずれた結果,2019年のギリギリになって焦って今頃焦って投稿したものです.全然間に合っていなくて申し訳ありませんでした...また,一応記事内の記号は統一するようにしていますが,画像内の記号まで統一はできていません...それでも良いという方はどうぞご覧ください.
本記事の概要
個人的な見解ですが,今回取り上げるCAM(Class Activation Map)は判断根拠をハイライトする方法として結構有名なものだと思います.後にも述べますが,CAMをより様々なネットワークに対応させたものにしたGrad-CAMと呼ばれる手法があるのですが,来年の某SAIとかでも使用した原稿が多く投稿されると思いますので,ここで一度整理したいと思いまとめました.
まずCAMについてまとめます.CAMとはXAI(Explainable AI)の手法の一つであり,主に画像認識のモデルで,特定のクラスに寄与したとされる入力領域をハイライトする手法です.ちなみに,解釈可能な手法には大きく分けて2つの軸で分けられた4つの分類があり,1つ目の軸は,モデル自体が解釈可能なものにする(Capsule Netなど)ものと,解釈不可能なモデルを解釈可能なモデルを解釈可能なものにするかどうかであり,2つ目の軸はモデル全体の解釈を試みる手法(Global)か,入力情報に対して解釈を試みる手法(Post-hoc)に分けられます.詳しく知りたい方は今は少し昔と比べて多くのサーベイ論文がArxiv上にあるので適当に調べて頂ければと思います.また,流石に元論文から持ってきた図とかのノーテーションを修正する元気はなかったので,手法が気になった方はご自身で論文をご参照くださればと....
ちなみに,CAMは下の図では,Post-hoc Local Explainationに該当すると思います.Post-hoc Grobal Explainationは,あまり知られていないですが,Activation Maximization(特定のユニットを最大に発火するような入力を生成するアルゴリズム)などが挙げられます.
 [Techniques for Interpretable Machine Learning](https://arxiv.org/abs/1808.00033)より引用
[Techniques for Interpretable Machine Learning](https://arxiv.org/abs/1808.00033)より引用
手法の説明
CAM[1]
CAMは,2016のCVPRにて発表されたCNNの判断根拠可視化の手法です.この手法はResNetのようにGlobal Average Poolingを使用するモデルに適応できる手法として提案されました.具体的な計算方法は下記のようになります.まず下記の図のようにGlobal Average Pooling -> 全結合層 -> 予測のようなモデルを考えます.クラスcのsoftmax前のスコアを$S_{c}$とし,$w_{k}^{c}$はクラスcと接続する重みであり,kは全結合層の添え字です(厳密にはk番目の特徴マップのGlobal Average Pooling後のスカラー値とクラスcのユニットをつなぐ重みです).$ f_{k}(x,y) $は,k番目の特徴マップの(x,y)座標に対応する出力です.そうすると,$S_{c}$は実は,下記のように表すことができることに気づきます.$\sum_{k} w_{k}^{c} \sum_{x, y} f_{k}(x, y)$はGlobal Average Poolingの計算ですね.(分母ないけど...まあ全ての特徴マップに同じ定数倍が入るだけなのでヒートマップにする段階で正規化することもあり影響はないですが).
S_{c}=\sum_{k} w_{k}^{c} \sum_{x, y} f_{k}(x, y)=\sum_{x, y} \sum_{k} w_{k}^{c} f_{k}(x, y)
つまり,$w_{k}^{c}$がk番目の特徴マップの重みづけることによってc番目のスコアが出力されるわけです.このことを利用して,$ \sum_{k} w_{k}^{c} f_{k}(x, y) $の部分を用いれば特徴マップの(x,y)に関しての重要さを表すヒートマップができるよねという具合です.

Grad-CAM [2]
CAMは特徴マップと最終層の重みの積で計算されることでヒートマップを作成していましたが、Grad-CAMはこの各特徴マップの重み付けの部分のところとGlobal Average Poolingの部分を逆伝搬時の勾配で代用できるというものでした.Grad-CAMは有名な手法なので、Global Average Pooling -> 全結合層の$ w_{k}^{c} $の部分を特徴マップへの勾配の各特徴マップ内の平均で代用できるよね?という手法です.これにより,様々なネットワークでCAMと同様のことができるようになったということで,幅広くCVの分野では使われています.基本的には下記のように変更があっただけですが,なぜ勾配で代用できるかは論文や解説サイトを実際に見た方が早いです.
w_{k}^{c}=\sum_{x} \sum_{y} \frac{\partial S^{c}}{\partial f_{k}(x, y)}

ちなみに論文内では,Guided Back-Propagationという手法と掛け合わせることで,CAM,Grad-CAMが特徴マップの大きさに沿った粒度での可視化をするという性質から,入力画像でのピクセル単位で可視化ができるGuided Grad-CAMが提案されています.
Guided Back-Propagation [3]
Guided Back-Propagationは手法として提案されたというよりも,全畳み込みネットワークの提案論文の中で紹介されたものであり,基本的な構想はシンプルで,もともとSaliency MapやSesitivity Anaysisのように逆伝播時の入力領域への勾配を見ることで寄与具合を見る研究はあったのですが,DeconvNetのように順伝播時に正の出力をそのままDeconvしてあげたら何か特徴のようなものが見られたという研究もあったので,その両方の着想を踏まえて,順伝播時に負だったユニットと逆伝播時に勾配が負だったユニットにはそれ以降の逆伝播をやめるという手法です.ただDeconvNetやGuided Back-Propagationはネットワークの重みを反映していないということがNIPS2018[4],ICML2018[5] で指摘されておりあまりつかわないほうが良いような気がします.
参考資料
Grad-CAMの資料は,ネットに結構あるので,調べれば無限に出てくると思いますので,割愛させていただきます.
Grad-CAM++ [6]
Grad-CAM++は,これまでの可視化の手法であるGuided BackpropagationやDeconvolutionのように逆伝播時の正の勾配に注目することでGrad-CAMを改良した手法です.
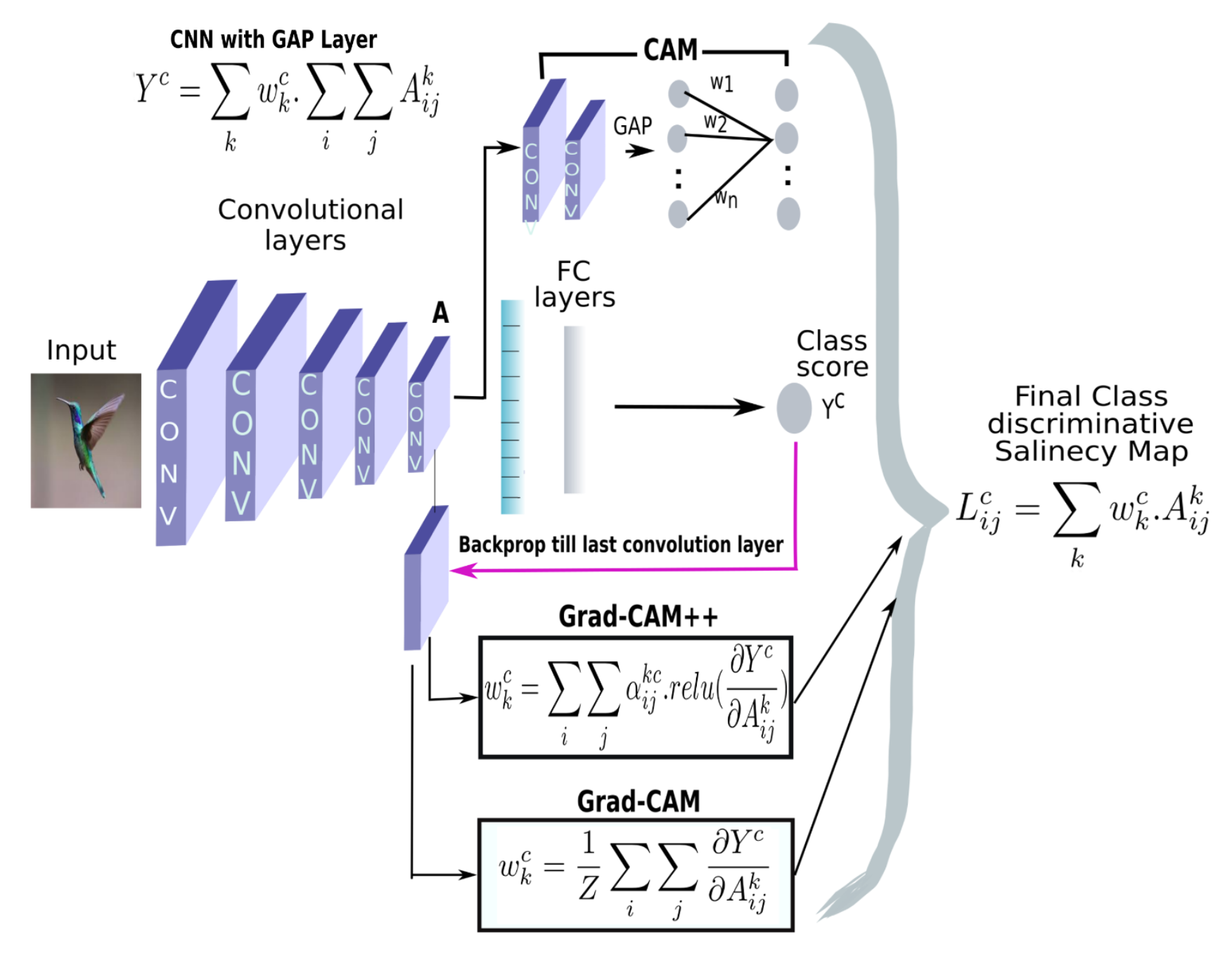
具体的な重み部分は以下のようになります.
w_{k}^{c}=\sum_{x} \sum_{y} \alpha_{x y}^{k c} \cdot \operatorname{relu}\left(\frac{\partial S^{c}}{\partial f_{k}(x, y)}\right)
数式を見ると,特徴マップの重みにさらに別の重み$ \alpha_{x y}^{k c} $がついていることに気づきます.これは何かと言いますと.少し思い出して欲しいのですが,そもそもCAMはクラスcのスコアである$ Sc $ が結局どこに繋がっていたのかということを見ているだけで,Grad-CAMでは特徴マップの重みがちょうど勾配の平均で計算できるという話になっただけであり,この重みは勝手に大小を決めてはいけないものなのです.そこで,勝手に重み $ w_{k}^{c} $ を計算する際に使用した勾配に制限をつけるのであればちゃんとつじつまが合うように調整しなければいけません.その調整部分が別の重み$ \alpha_{x y}^{k c} $です.この$ \alpha_{x y}^{k c} $を計算するために筆者は方程式を立てて(仮に重みがそのように置かれた場合にどう計算されるのか?)解いていました.その結果下記にように重み$ \alpha_{x y}^{k c} $は以下のようになります.$Y^{c} = \text{exp}(S^c)$です.
\alpha_{x y}^{k c}=\frac{\frac{\partial^{2} Y^{c}}{\partial f_{k}(x, y)^{2}}}{2 \frac{\partial^{2} Y^{c}}{\partial f_{k}(x, y)^{2}}+\sum_{a} \sum_{b} f_{k}(a, b)\frac{\partial^{3} Y^{c}}{\partial f_{k}(x, y)^{3}}}
なんだか複雑そうですが,基本的には3回微分の結果を使っているだけなので,そこまで難しい事ではないと思います.いやいや,そもそも複数回の微分の計算自体が計算量が多いんだよっていう話ですが,実は逆伝播をする場所を*$ S_c$ではなく,$ \text{exp}(S_c)$にして,活性化関数に$\text{ReLU}$*を使用した場合に限ってはそうではなく,2,3回微分は以下のように簡単に計算できるのです.正直僕はここが一番参考になるように感じました.
\frac{\partial^{2} Y^{c}}{\partial f_{k}(x, y)^{2}}=\exp \left(S^{c}\right)\left[\left(\frac{\partial S^{c}}{\left(\partial f_{k}(x, y)\right)}\right)^{2}+\frac{\partial^{2} S^{c}}{\partial f_{k}(x, y)^{2}}\right]
この第二項の計算の際に活性化関数として$ \text{ReLU}$を使用していると,二回微分時に0になり,うまい具合に項が消えます.つまり,複数回微分は以下のうように階乗の形で表現できるのです.
\frac{\partial^{2} Y^{c}}{\partial f_{k}(x, y)^{2}}=\exp \left(S^{c}\right)\left(\frac{\partial S^{c}}{\partial f_{k}(x, y)}\right)^{2}
正直CAM系の手法は勾配の制約の部分をいろいろいじってみた系の論文とかは結構あると思うのですが,個人的にそれ結局$ S_c$にならなくない?って疑問に思うものがほとんどだったので,そういう意味でこの論文は有用だと思いました.
参考資料
Grad-CAM++は実際に筆者のコードを見たり.下記の記事などが参考になると思います.
・最新手法!「Grad-CAM++」のレビューと実装
Pyramid Grad-CAM [7]
Pyramid Grad-CAMは,U–NetのようにSkipな接続を繰り返し行う分類モデルに対して、中間層にGrad-CAMを繰り返すことで解像度を上げた可視化を可能にした手法です.具体的には下記の図のようなネットワーク構造のモデルの場合に,各層に対してGrad-CAMを適応しています.正直ネットワークが特殊な場合にしか使えないので,紹介するか悩みましたが,一応上記の勾配を少しいじりました系論文よりは参考になると思いますので紹介します.今までのものとは表記が違うので少し混乱を招くかもしれませんが,要するに各層に関してGad-CAMの最後の$\text{ReLU}$の処理を行わないものを繰り返し行い,アップサンプリングしたものを層ごとにくっつけているというものです.
\text{PGCAM}_{c}=\sum_{p=1}^{5} \operatorname{ReLU}\left(\sum_{k_{p}} \sum_{i} \sum_{j} \frac{\partial L^{c}}{\partial f_{i j}^{k_{p}}} f_{k_{p}}^{s_{p}}(X, Y)\right)=\sum_{p=1}^{5} \operatorname{GradCAM}_{c}^{s_{p}}

CCAM(Common Component Activation Map) [8]
CCAMは, 例えばImageNet内のクラスに存在しないようなクラスに対する可視化を行いたいような問題に対する手法です.
N個の画像集合$I= \{{I_{1}, \ldots, I_{N}} \}$とそれに伴うネットワークのソフトマックス後の出力の集合$V= \{{V_{1}, \ldots, V_{N}} \}$を用いて,以下のようなN個の出力の平均ベクトルを$ G $を計算します.
G=\frac{1}{N} \sum_{i} V_{i}
そして,画像$ I_i $のヒートマップとして使用するヒートマップを以下のようにして計算します.
M^{i}(x, y)=\sum_{c \in K(G)} G_{c} \sum_{k} w_{k}^{c} f_{k}(x, y)
$ \sum_{k} w_{k}^{c} f_{k}(x, y) $の部分はCAMと同じですが,$ \sum_{c \in K(G)} G_{c} $の部分が(あっているのかわからないですが),おそらく平均ベクトル$ G $のk番目の要素が$ G_{k}$と表されているとしたら,$K(G)$は,入力$I_i$に対する出力のうち上位K個のクラスのことをだと思います.つまり,上位K個の特徴マップをそれぞれCAMによって作成しますが,そのここのクラスのヒートマップの重みづけを$ G_{k}$によって行うというものです(だと思います).

Smooth Grad-CAM++ [9]
Smooth Grad-CAM++は,Smooth Gradの考え方とGrad-CAM(++)の考え方を組み合わせたもので,重み付けとなる部分をSmooth Gradのように入力にノイズを加えて逆伝播させたものの平均を取ることで代用しています.

Smooth Grad [9]
Smooth Gradは,Saliency Mapなどの入力層の勾配に注目した手法では,入力のわずかな変化に敏感に変化してしまう問題があったことを緩和するために提案された手法です.具体的には入力に正規分布からのランダムノイズを追加し,今までの可視化の手法を利用するというものです.具体的な計算は下記のようになっています.通常のヒートマップを$ M_{c}(x)=\partial S_{c}(x) / \partial x $とすると,下記のようになります.入力にノイズを加える+マップを平均化することで,よりノイズの少ないヒートマップを作成できるようになります.
\hat{M}_{c}(x)=\frac{1}{n} \sum_{1}^{n} M_{c}\left(x+\mathcal{N}\left(0, \sigma^{2}\right)\right)
このSmooth Gradの考え方と先ほど紹介したGrad-CAM++を組み合わせるだけなので発想はシンプルです.実際の計算は下記のようにするだけです.$ D_{k}^{n} $はk番目のヒートマップのn回微分の記号です.
\alpha_{x, y}^{k c}=\frac{\frac{1}{n} \sum_{1}^{n} D_{1}^{k}}{2 \frac{1}{n} \sum_{1}^{n} D_{2}^{k}+\sum_{a} \sum_{b} A_{a, b}^{k} \frac{1}{n} \sum_{1}^{n} D_{3}^{k}}
基本的にはGrad-CAM++の勾配計算の部分をSmooth Gradのようにノイズを加え複数回計算した平均で代用するというものです.
Score-CAM [10]
出力層からの勾配を計算するのは良いとして,勾配は入力層のわずかな変化に対して(特に入力層は)大きく変化してしまうという問題がある.これはこの論文だけでなく,様々な論文で言われている.そこで,勾配に頼ることなく,ヒートマップを作成で切ることに利点があります.(ただ個人的にGrad-CAMって,Adversalial Exampleに強いのが個人的に良いところだと思ってたのにスコアで重み付けしたら効果無くなるのでは?って思うんだけどどうなんだろうか...?).雰囲気はCAM系列というよりもRISEとかの方が近いですね.具体的な計算方法は下記です.
基本的に順伝播時の特徴マップの算出までは同じですが,特徴マップの重みづけの際に,一度それぞれの特徴マップを拡大+保存しておいて,再度特徴マップごとにマスク処理をして入力します.マスク処理した($ M^{k}=A^{k} \cdot I $)ネットワークのスコア$ S_{k}=\operatorname{Softmax}\left(F\left(M^{k}\right)\right) $を重みとして使用します.

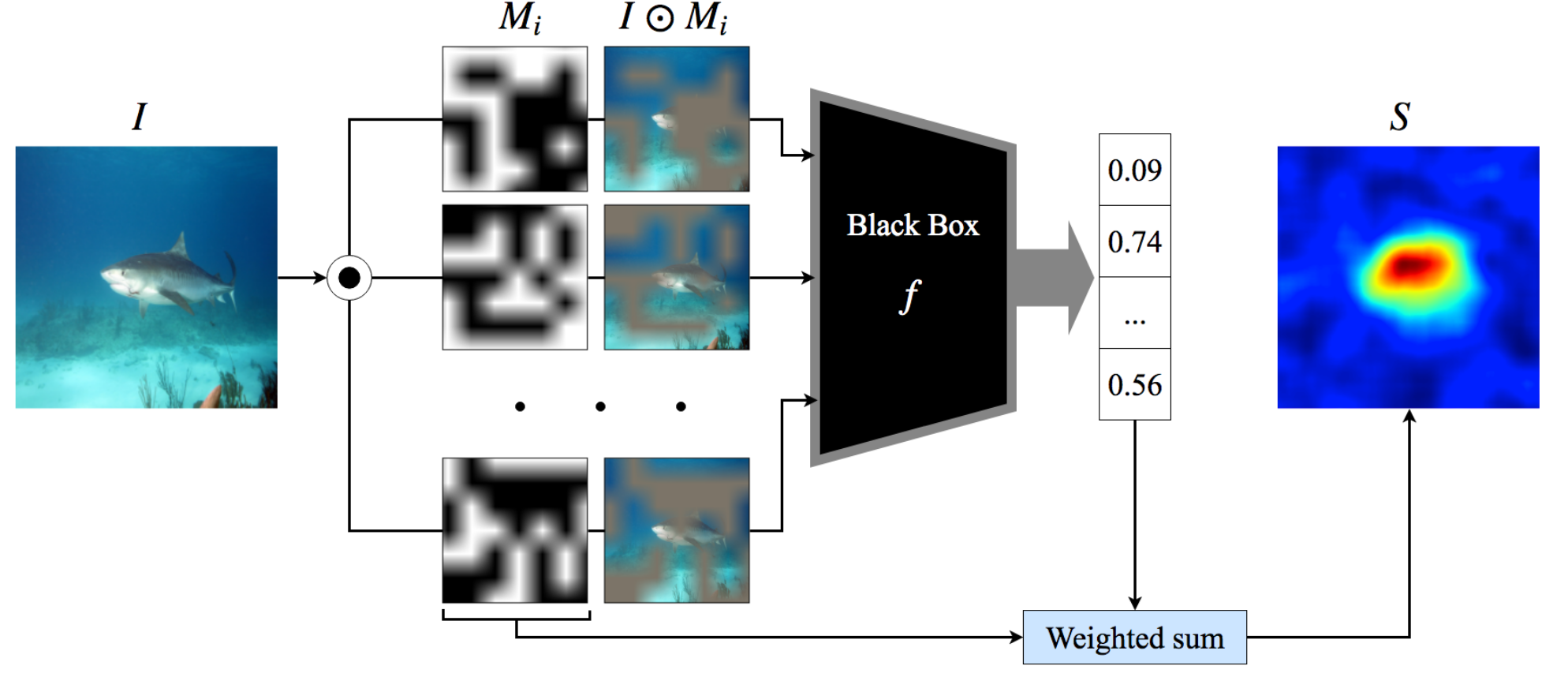
RISE [11]
RISEとは,LIMEの画像バージョンですが,LIMEをそのまま画像に適応する場合はスーパーピクセルで分割する手法が一般的だと思いますが,ここではほとんどランダムなマスクを作成してLIMEのようなことをしています.
参考資料
Score-CAMは比較的新しい手法ですが,Qiitaで再現実験をおこなっている方がいるので大変参考になると思います.個人的にこの方がさらっと提案しているFaster-Score-CAMは,確かに早いのかもしれませんが,有効性の評価をしていないので,ぜひ有効性を評価して再度論文として見てみたいところです.
・kerasでScore-CAM実装.Grad-CAMとの比較
Grad-CAMは完全に正義なのか?
ネットワーク構造にそこまで依存しない,去年XAI界隈を騒がせた(と思っている)論文[4][5]でもモデルの重みに依存した可視化をしています.一見問題がないように思われるが,昨今の研究では,ネットワークに重みを追加することで任意の領域のヒートマップを出力させることができる手法が提案されています[12].言い換えれば,完全にブラックボックスなモデルと,その判断根拠となる可視化の結果が添付されるような状況を考えた際に,その精度をほとんど落とすことなく,任意の入力(画像だと絵文字のマークのように)に反応するよう悪意ある加工をしたり,完全にまっさらなヒートマップを出力させるようにできるということです.つまり,企業側などがモデルの製品の判断根拠として提示するヒートマップが内部で適当な処理をすることで,全く信用できないヒートマップも作る手法を提案しています.
感想
この論文ではあまり具体的には述べられていないと思いますが,個人的に精度を変えずに任意のヒートマップを作成できるのはかなり怖いなと思いました.例えば,Grad-CAMを使ったら実は背景しか見ていないモデルを作っていたことに気づくという状況(これは結構多くのデータセットに存在していて,例えば分類クラスに狼が入ったモデルを学習したのちにGrad-CAMをしたら,実はモデルは狼の領域とは関係なく,背景の雪景色に判断根拠が存在していたという例もあります)を考えた際に,悪意を持ってモデル作成者がここが寄与していると信じたい部分(腫瘍とか血腫とか)によく反応するようなGrad-CAMの出力を変更できるからです.こういうヒートマップを精度を変えることなく,任意に変えてしまうのはこれまであまりない観点だったので,勉強になった論文でした.

まとめ
CAM系の手法をいろいろ自分なりにまとめてみました.少しまとめ方が雑ですが参考になれば幸いです.また,何か間違い/改良した方が良い点などがございましたら,ご連絡いただければ幸いです.
参考文献
[1] Learning Deep Features for Discriminative Localization, B. Zhou, A. Khosla, A. Lapedriza, A. Oliva and A. Torralba, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, 2016, pp. 2921-2929.
[2] Grad-cam: Visual explanations from deep networks via gradient-based localization,R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam,D. Parikh, D. Batra, et al. InICCV, pages 618–626, 2017.
[3] Striving for simplicity: The all convolutional net,Springenberg, Jost Tobias, et al arXiv:1412.6806 (2014).
[4] Sanity Checks for Saliency Maps, Julius Adebayo, Justin Gilmer, MichaelMuelly, Ian Goodfellow, Moritz Hardt, Been Kim, Advances in NeuralInformation Processing Systems 31, (2018)
[5] A Theoretical Explanation for Perplexing Behav-iors of Backpropagation-based Visualizations: WeiliNie, Yang Zhang, Ankit Patel, International Confer-ence on Learning Representations 2018, (2018)
[6] Grad-cam++: Generalized gradient-based visual explanations for deep convolutional networks, Chattopadhyay, A. Sarkar, P. Howlader, and V. N. Balasubramanian,CoRR,abs/1710.11063, 2017
[7] Robust Tumor Localization with Pyramid Grad-CAM, S. Lee, J. Lee, J. Lee, C.-K. Park, and S. Yoon. arXiv preprintarXiv:1805.11393, 2018
[8] Localizing Common Objects Using Common Component Activation Map, Weihao Li, Omid Hosseini Jafari, Carsten Rother; The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2019, pp. 28-31
[9] Smooth Grad-CAM++: An Enhanced Inference Level Visualization Technique for Deep Convolutional Neural Network Models Daniel Omeiza, Skyler Speakman, Celia Cintas, Komminist Weldermariam, arXiv:1908.01224
[9] SmoothGrad:removing noise by adding noise, Daniel Smilkov, Nikhil Thorat, Been Kim,Fernanda Vi egas, Martin Wattenberg, International Conference on Machine Learning Workshop 2018, (2018)
[10] Score-CAM:Improved Visual Explanations Via Score-Weighted Class Activation Mapping, Wang, Haofan & Du, Mengnan & Yang, Fan & Zhang, Zijian. arxiv.org/abs/1910.01279
[11] RISE: Randomized Input Sampling for Explanation of Black-box Models. V Petsiuk, A Das, K Saenko. British Machine Vision Conference (BMVC), 2018. 19, 2018.
[12] How to Make CNNs Lie: the GradCAM Case, Tom J Viering, Ziqi Wang, Marco Loog, Elmar Eisemann (Delft University of Technology & University of Copenhagen), BMVC2019