動的モード分解: Dynamic Mode Decomposition

更新履歴

• 2024/05/30: 初版
• 2025/02/27: exact DMDのモード計算を固有値でスケール調整（参考: Tu et al., 13)
• 2025/04/14: exact DMDとstandard DMDの比較における誤差解析の考察を修正・簡潔化

はじめに

職場でDMDの知識が求められる案件があったので、アウトプットとして投稿。
参考はData-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Controlの第七章。久々に英語の書籍を読むのが辛かった。
今回はexact DMDのアルゴリズムを理解して、公開されている二次元円柱周りの流れ場データに対して、実際にDMDを適用することをゴールとする。

概要

Dynamical Sytems=力学系というのは、時間経過に伴い、ある法則にしたがって変化する系、また或いは、初期状態が与えられた時、その後の全ての状態量の変化が決定される系のことを指す。

その概念は、かつてポアンカレが天体の運動を研究していた時に端を発する。彼は2つの天体による運動は比較的単純であることを発見したが、3つ目の天体が加わると運動が非常に複雑になり、その結果として予測が困難になることを明らかにした。この発見は、カオス理論の初期の形態と見なされている。その後、この理論は古典機械システム、電子回路、流体、気候学、金融、経済など多岐にわたる分野での数学的モデリングへと発展した。

取り分け近年では、支配方程式が未知である一方で、観測データが十分にあるため、解析的なアプローチからData-Drivenなアプローチへと移行している。

Dynamical Systems

本章では、近年のData-Driven型Dynamical Systemsへの導入の準備として、力学系の表記法を導入し、主要な動機と課題について述べる。

基本定義

初めに、Dynamical Systemsの数学的記述を導入する。
時間を $t,s\in T$ 、空間を $\boldsymbol{x}\in H$ としたとき、

\begin{cases}
\text{恒等性：}&\boldsymbol{f}(\boldsymbol{x}, 0) = \boldsymbol{x}_0 \\\\
\text{結合法則:}&\boldsymbol{f}(\boldsymbol{f}(\boldsymbol{x}, t), s) = \boldsymbol{f}(\boldsymbol{x}, t+s)
\end{cases}

この条件を満足する接バンドル $\boldsymbol{f}$ を含めた組み合わせを力学系と呼ぶ。参考書では、写像 $\boldsymbol{f}$ がリプシッツ連続であることを前提に話が進むので、上記2つの定義から以下のように一階微分方程式が容易に求められる。

\begin{align}
\boldsymbol{x}(t)&=\boldsymbol{f}(\boldsymbol{x}_0, t) \\
\Rightarrow \frac{\partial}{\partial t}\boldsymbol{x}(t)&=\frac{\partial}{\partial t}\boldsymbol{f}(\boldsymbol{x}_0, t) \\
&=\left.\frac{\partial\boldsymbol{f}}{\partial t}\right|_{(\boldsymbol{x}, t)}
\end{align}

参考書では、これをより簡潔に（というか物理の慣習的に?） $\frac{d}{dt}\boldsymbol{x}=\boldsymbol{f}(\boldsymbol{x}, t; \boldsymbol{\beta})$ と記述されている。
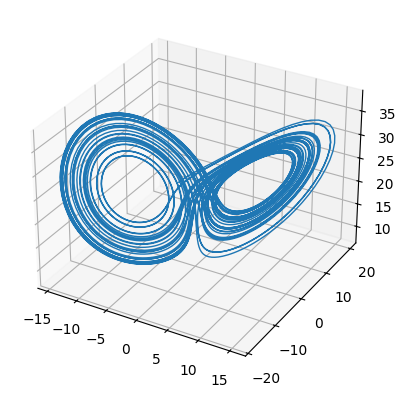
実例として、ローレンツ系の方程式を考え、pytonで可視化してみる。

支配方程式

\begin{cases}
\frac{\partial x}{\partial t}=\sigma(y-x)\\
\frac{\partial y}{\partial t}=x(\rho -z)-y\\
\frac{\partial z}{\partial t}=xy-\beta z
\end{cases}

可視化コード（python）

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

def lorenz(x_y_z, _, sigma, beta, rho):
    x, y, z = x_y_z
    return [sigma * (y - x), x * (rho - z) - y, x * y - beta * z]

# Initial conditions
x0 = (0., 1., 20.)
eps = 0.01
t = np.arange(0, 50, eps)

# Lorenz attractor parameters
sigma = 10.0
beta = 2.
rho = 25.0

# Solving the Lorenz system
x_t = odeint(lorenz, x0, t, args=(sigma, beta, rho))

# Extracting individual components
x, y, z = x_t.T

# Creating a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z, linewidth=1)
plt.show()

可視化結果

Discrete-Time Systems

前章では連続力学系について紹介したが、本章は離散力学系について述べる。
離散力学系は、実験データやデジタルコントロールの分野ではより重要な系（マシンが扱えるから）となる。

基本定義

基本定義は以下の漸化式として表現できる。

\boldsymbol{x}_{k+1}=\boldsymbol{F}(\boldsymbol{x}_{k})

この離散力学系の基本定義は前述の連続力学系の基本定義から導出することが出来る。
十分に小さなステップ時間 $\Delta t$ を取ることで、多様体 $\boldsymbol{x}_{k}=\boldsymbol{x}(k\Delta t)$ となるので、

\begin{align}
&&{\text 連続力学系基本定義: }\frac{d}{dt}\boldsymbol{x}(t)&=\boldsymbol{f}(\boldsymbol{x}(t)) \\
&\Rightarrow&\boldsymbol{x}(t)&=\int_{0}^{t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau \\
&\Rightarrow&\boldsymbol{x}(k\Delta t+\Delta t)&=\int_{0}^{k\Delta t+\Delta t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau \\
&&&=\int_{0}^{k\Delta t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau+\int_{k\Delta t}^{k\Delta t+\Delta t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau \\
&&&= \boldsymbol{x}(k\Delta t)+\int_{k\Delta t}^{k\Delta t+\Delta t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau \\
&i.e.&\boldsymbol{x}(t_o+t)=\boldsymbol{F}_t(\boldsymbol{x}(t_0))&=\boldsymbol{x}(t_0)+\int_{t_0}^{t_0+t}\boldsymbol{f}(\boldsymbol{x}(\tau))d\tau
\end{align}

この離散力学系は $\Delta t$ を小さくすればする程、連続力学系へ近づき、計算機科学の分野では一般的な概念となっている。

線形力学系とスペクトル分解

線形力学系は閉形式の解を持つので、可能な限りそれとして扱うのが推奨される。

\begin{align}
\frac{d}{dt}\boldsymbol{x}(t)&=\boldsymbol{Ax}(t) \\
\Rightarrow \boldsymbol{x}(t_0+t)&=e^{\boldsymbol{A}t}\boldsymbol{x}(t_0)
\end{align}

ここで、行列指数関数 $e^{\boldsymbol{A}}:=\sum^\infty_k \frac{1}{k!}A^k$ である。
この力学系の特性は、行列 $\boldsymbol{A}$ の固有行列および固有値に依存する。行列 $\boldsymbol{A}$ のスペクトル分解（固有値分解）は、

\boldsymbol{AT}=\boldsymbol{T\Lambda}

と表現される。
ただし、行列 $\boldsymbol{A}$ は $n$ 個の相違なる固有値を持ち、行列 $\boldsymbol{\Lambda}$ は対角成分に $\lambda_j$ を持つ対角行列、行列 $\boldsymbol{T}$ は固有値 $\lambda_j$ に付随する線形独立固有ベクトル $\xi_j$ を列に持つ。（即ち、 $\boldsymbol{T}=(\xi_1, \xi_2,...,\xi_n)$ ）
特に、上記の場合は行列 $\boldsymbol{A}$ が対角化可能であるので、 $\boldsymbol{A}=\boldsymbol{T\Lambda T}^{-1}$ と記述出来るので、

\begin{align}
\boldsymbol{x}(t_0+t)&=e^{\boldsymbol{A}t}\boldsymbol{x}(t_0) \\
&=e^{\boldsymbol{T\Lambda T}^{-1}t}\boldsymbol{x}(t_0) \\
&=\left\{\sum^\infty_{k=0} \frac{1}{k!}(\boldsymbol{T\Lambda T}^{-1}t)^k\right\}\boldsymbol{x}(t_0) \\
&=\left\{\sum^\infty_{k=0} \frac{1}{k!}\boldsymbol{T}(\boldsymbol{\Lambda}t)^k\boldsymbol{T}^{-1}\right\}\boldsymbol{x}(t_0) \\
&=\boldsymbol{T}e^{\boldsymbol{\Lambda}t}\boldsymbol{T}^{-1}\boldsymbol{x}(t_0)
\end{align}

重複する固有値を持つ際には、ジョルダン標準を用いることで表現可能だが、参考書第七章では解説されていないため、割愛する。
ところで、上記式に置いて両辺左から $\boldsymbol{T}^{-1}$ を掛けると

\boldsymbol{T}^{-1}\boldsymbol{x}(t_0+t)=e^{\boldsymbol{\Lambda}t}\boldsymbol{T}^{-1}\boldsymbol{x}(t_0)

さらに、 $\boldsymbol{z}=\boldsymbol{T}^{-1}\boldsymbol{x}$ と置換して

\begin{align}
&&\boldsymbol{z}(t_0+t)&=e^{\boldsymbol{\Lambda}t}\boldsymbol{z}(t_0) \\
&\Rightarrow&\frac{d}{dt}\boldsymbol{z}&=\boldsymbol{\Lambda}\boldsymbol{z} \\
&\Rightarrow&\frac{d}{dt}z_j&=\lambda_j z_j\quad\because \boldsymbol{\Lambda}\text{ is a diagonal matrix}
\end{align}

このように、はじめに導入した線形力学系の式へと回帰できた。
即ち、ベクトル $\boldsymbol{x}$ を固有空間へマッピングすることで、次元ごとの単純な力学系で表現することが可能である。

Dynamic Mode Decomposition (DMD)

Dynamic Mode Decomposition（以下、DMD）は、シュミットが流体力学分野で開発した、高次元データから時空間構造を抽出する次元削減手法である。そのアルゴリズムは特異値分解（SVD）や固有直交分解（POD）に基づくものだが、これらの手法が空間的な相関だけ基づく階層化を行うのに対して、DMDは時間情報を考慮に入れることが出来る。つまり、DMDアルゴリズムは、空間的次元削減のためのSVDと、時間的周波数同定のための高速フーリエ変換（FFT）のいいとこ取りアルゴリズムなのだ。しかし、そのトレードオフとして制約的になることに留意する必要がある。

特に線形システムの場合、DMDはクープマン作用素の近似となり、非線形力学系を線形演算により近似的に解析することが出来る。さらに、実験データや数値データに等しく有効であり、支配方程式に依存しないデータ駆動型の特性評価ができる。

この様な特性や、数値的な柔軟性もあり、DMDは近年では非常に人気が高まっていると言う。

DMDアルゴリズム概要

DMDアルゴリズムはいくつか提案されているが、ここではTuらによるexact DMDを紹介する。従来手法がデータの一様サンプリングを要求してくるのに対し、exact DMDは不均一サンプリングにも対応できる。

早速、数学的定式化を導入する。時間展開する系のスナップショットの組を以下のように表す。

\text{snapshot}:=\{\boldsymbol{x}(t_k), \boldsymbol{x}(t'_k)\}_{k=1}
^m

ここで、系の挙動を表現するのに十分に小さい $\Delta t$ を用いて、漸化式 $t'_k=t_k+\Delta t$ が満足されるものとする。これらの列ベクトルを束ねて、次のような行列を定義する。

\begin{align}
\boldsymbol{X}=
\begin{bmatrix}
| & | & & | \\
\boldsymbol{x}(t_1) & \boldsymbol{x}(t_2) & \cdots & \boldsymbol{x}(t_m) \\
| & | & & |
\end{bmatrix}\\\\
\boldsymbol{X}'=
\begin{bmatrix}
| & | & & | \\
\boldsymbol{x}(t'_1) & \boldsymbol{x}(t'_2) & \cdots & \boldsymbol{x}(t'_m) \\
| & | & & |
\end{bmatrix}
\end{align}

さて、改めてDMDの目的は、以下に式を最も満足する線形演算 $\boldsymbol{A}$ の固有値、固有ベクトルを求めることである。固有値は複素数であり、その実部はモードの成長or減衰の率を表し、虚部はモードの振動周波数を示す。したがって、固有値を解析することで、システムが時間と共にどのように発展していくかを把握できる。

\boldsymbol{X}'\simeq\boldsymbol{AX}

シュミットによる元の定式化では一様サンプリングを仮定しており、その場合 $\boldsymbol{x}_k=\boldsymbol{x}(k\Delta t)$ と記述できるので、

\begin{align}
&&\boldsymbol{X}'&\simeq\boldsymbol{AX}\\
&\Rightarrow&
\left(
\boldsymbol{x}(t_1)\ \boldsymbol{x}(t_2)\ \cdots\ \boldsymbol{x}(t_m) \right)
&\simeq\boldsymbol{A}
\left(
\boldsymbol{x}(t_2)\ \boldsymbol{x}(t_3)\ \cdots\ \boldsymbol{x}(t_{m+1}) \right)\\
&\Rightarrow&\boldsymbol{x}_{k+1}&\simeq\boldsymbol{Ax}_k
\end{align}

即ち、最適な $\boldsymbol{A}$ は以下のように与えられる。

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\boldsymbol{A}=\argmin_{\boldsymbol{A}}\|\boldsymbol{X}'-\boldsymbol{AX}\|_F
=\boldsymbol{X}'\boldsymbol{X}^\dagger

ただし、 $\|\cdot\|_F$ はフロベニウスノルム、 $^\dagger$ は擬似逆行列を表す。

フロベニウスノルムについてはこちら

フロベニウスノルムは2つの行列がどのくらい違っているかを測るための尺度のひとつである。 行列 $\boldsymbol{A}\in\mathbb{C}^{n\times m}, n\geq m$ を考えたとき、その特異値も $\sigma_k$ と表現して

\|\boldsymbol{A}\|_F=\sqrt{\sum_i^m\sum_j^n\mid a_{ij}\mid^2}
=\sqrt{\mathrm{tr}(A^*A)}=\sqrt{\sum_{i=1}^m \sigma^2_i}

このノルムはフロベニウスノルムと呼ばれ、これを目的関数とした場合の最小化問題の解がSVD(what we call truncated SVD)である、という内容がEckart-Youngの定理である。

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\argmin_{\tilde{\boldsymbol{X}}, \mathrm{s.t. rank}(\tilde{\boldsymbol{X}})=r}\|\boldsymbol{X}-\tilde{\boldsymbol{X}}\|_F
=\tilde{\boldsymbol{U}}\tilde{\boldsymbol{\Sigma}}\tilde{\boldsymbol{V}}^*

ここでは深掘りは行わないが、上記で吟味された行列 $\boldsymbol{A}$ が後述するクープマン作用素（実測定関数 $\boldsymbol{g}(\boldsymbol{x})=\boldsymbol{x}$ の場合）に似ていることに着目する。 $\boldsymbol{A}$ がクープマン作用素の線形測定有限部分空間の近似であることから、やはり行列 $\boldsymbol{A}$ についての固有値 $\Lambda$ と固有ベクトル行列 $\boldsymbol{\Phi}$ を求めることが目的となる。

\boldsymbol{A\Phi}=\boldsymbol{\Phi\Lambda}

exact DMDアルゴリズム

前節で言及した式のように、行列 $\boldsymbol{A}$ から固有値、固有ベクトルを求めることは理論的には単純であるが、リアルワールドデータのように高次元になってくると、スペクトル分解どころか、 $\boldsymbol{A}$ を正しく表現することすらままならないと言う。

DMDアルゴリズムは次元削減を利用して、 $\boldsymbol{A}$ を直接使った明示的な計算を必要とせずに、スペクトル分解を実現する。さらに、ある特定の条件下では、これらの縮小行列による近似が行列 $\boldsymbol{A}$ の固有ベクトルに完全一致する。(exact DMD)

以下より、その手順について解説する。

Step 1.

はじめに、系の状態 $\boldsymbol{X}\in\mathbb{C}^{n\times m}$ のSVDを行う。
部分ユニタリ行列 $\tilde{\boldsymbol{U}}\in\mathbb{C}^{n\times r}$ と $\tilde{\boldsymbol{V}}\in\mathbb{C}^{r\times m}$ 、非負実対角行列 $\tilde{\boldsymbol{\Sigma}}\in\mathbb{C}^{r\times r}$ を用いて、

\boldsymbol{X}\simeq\tilde{\boldsymbol{U}}\tilde{\boldsymbol{\Sigma}}\tilde{\boldsymbol{V}}^*

多くのケースで、 $\boldsymbol{X}$ はtall-skinnyな行列であり、階数 $r$ をどう選ぶかもDMDの過程でひとつ問題となる。（参考:Gavish and Donoho）

Step. 2

前節より、行列 $\boldsymbol{A}$ は擬似逆行列 $\boldsymbol{X}$ を用いて得ることができ、

\begin{align}
\boldsymbol{A}&=\boldsymbol{X}'\boldsymbol{X}^\dagger \\
&=\boldsymbol{X}'\left(\tilde{\boldsymbol{U}}\tilde{\boldsymbol{\Sigma}}\tilde{\boldsymbol{V}}^*\right)^{*}\\
&=\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\tilde{\boldsymbol{U}}^*
\end{align}

ここで、興味があるのは行列 $\boldsymbol{A}$ の固有値であるので、 $\boldsymbol{X}$ の左特異ベクトル縮約行列 $\tilde{\boldsymbol{U}}$ による行列 $\boldsymbol{A}$ の類似変換をすれば、

\begin{align}
\tilde{\boldsymbol{A}}&=\tilde{\boldsymbol{U}}^*\boldsymbol{A}\tilde{\boldsymbol{U}}\\
&=\tilde{\boldsymbol{U}}^*\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\tilde{\boldsymbol{U}}^*\right)\tilde{\boldsymbol{U}}\\
&=\tilde{\boldsymbol{U}}^*\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\quad\because\boldsymbol{U}^*\boldsymbol{U}=\boldsymbol{E}
\end{align}

このように、同じ $\boldsymbol{A}$ と同じ固有値を持つ縮約行列 $\tilde{\boldsymbol{A}}$ をより単純な行列の積から得ることができる。

類似変換の固有値保存についてはこちら

部分ユニタリ行列 $\boldsymbol{U}\in\mathbb{C}^{n\times r}$ による類似変換の永年方程式の左辺を展開する。

\begin{align}
|\boldsymbol{U}^*\boldsymbol{A}\boldsymbol{U}-\lambda\boldsymbol{E}|
&=|\boldsymbol{U}^*\boldsymbol{A}\boldsymbol{U}-\lambda\boldsymbol{U}^*\boldsymbol{U}|\\
&=|\boldsymbol{U}^*\left(\boldsymbol{A}-\lambda\boldsymbol{E}\right)\boldsymbol{U}|\\
&=|\boldsymbol{A}-\lambda\boldsymbol{E}|=0
\end{align}

よって、固有値が保存されることがわかる。ただし、固有ベクトルの保存については保証されない。

行列 $\boldsymbol{U}$ による縮約状態へのマッピング $\tilde{\boldsymbol{x}}=\tilde{\boldsymbol{U}}^*\boldsymbol{x}$ を実施することで、縮約行列 $\boldsymbol{A}$ による線形ダイナミクス $\tilde{\boldsymbol{x}}_{k+1}=\tilde{\boldsymbol{A}}\tilde{\boldsymbol{x}}_k$ に置き換えることができる。（次元削減）

Step. 3

前Step.で求めた縮約行列 $\tilde{\boldsymbol{A}}$ のスペクトル分解を計算する。

\tilde{\boldsymbol{A}}\boldsymbol{W}=\boldsymbol{W\Lambda}

対角行列 $\boldsymbol{\Lambda}$ の対角成分はDMDの固有値であり、元の行列 $\boldsymbol{A}$ のそれと一致する。固有ベクトル行列 $\boldsymbol{W}$ は $\tilde{\boldsymbol{A}}$ の固有ベクトルからなる行列で、対角化する座標変換を行う。

Step. 4

さて、ここで漸くDMDの固有ベクトル行列 $\boldsymbol{\Phi}$ が導出できるようになる

\begin{align}
&&\tilde{\boldsymbol{A}}\boldsymbol{W}
&=\boldsymbol{W\Lambda}\\
&\Rightarrow&\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\right)\tilde{\boldsymbol{A}}\boldsymbol{W}
&=\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\right)\boldsymbol{W\Lambda}\\
&\Rightarrow&\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\right)\left(\tilde{\boldsymbol{U}}^*\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\right)\boldsymbol{W}
&=\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\right)\boldsymbol{W}\boldsymbol{\Lambda}\\
&\Rightarrow&\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\tilde{\boldsymbol{U}}^*\right)\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}\right)
&=\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}\right)\boldsymbol{\Lambda}\\
&\Rightarrow&\boldsymbol{A}\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}\right)
&=\left(\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}\right)\boldsymbol{\Lambda}\\
&\Rightarrow&\boldsymbol{\Phi}&=\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}
\end{align}

シュミットの元の論文中では、 $\boldsymbol{\Phi}=\tilde{\boldsymbol{U}}\boldsymbol{W}$ とされており、projected modesと呼ばれている。先ほど導出した固有ベクトル行列 $\boldsymbol{\Phi}$ が $\boldsymbol{X}'$ の列空間に存在するのに対し、projected modesは $\boldsymbol{X}$ の列空間に存在することになる。線形変換 $\boldsymbol{A}$ の定義は $\boldsymbol{A}:=\boldsymbol{X}'\boldsymbol{X}^\dagger$ であることから、本来であれば $\boldsymbol{\Phi}$ は $\boldsymbol{X}'$ の列空間にあるべきだが、実際の $\boldsymbol{X}$ と $\boldsymbol{X}'$ の列空間はほぼ同じ（直感的で良い）なので、あまり大きな問題にはならない。

従来のDMDと本書籍が解説に注力しているexact DMDの違いはまさにここで、数学的正確性と数値計算的正確性を天秤かけて前者を取ったのが、exact DMDである。

固有値 $\lambda=0$ に対するDMDモードが $\boldsymbol{\phi}=\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{w}=0$ の場合、 $\boldsymbol{\phi}=\tilde{\boldsymbol{U}}\boldsymbol{w}$ を用いると良い。

第二版追記
Tu et al., 13の式 $(2)$ によると、exact DMDのモードは

\boldsymbol{\Phi}=\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{W}\boldsymbol{\Lambda}^{-1}

として定義されており、モードが対応する固有値でスケールされている。こちらの式で計算を行った方が精度が上がったため、これを修正点とした。しかしながら、依然としてstandard DMDの方が精度は高い

歴史的背景

これは余談として記されているのだが、元々 $\boldsymbol{X}$ と $\boldsymbol{X}'$ は以下のように、連続したスナップショットをズラした形で記述されていた。

\begin{align}
\boldsymbol{X}&=
\begin{bmatrix}
| & | & & | \\
\boldsymbol{x}_1 & \boldsymbol{x}_2 & \cdots & \boldsymbol{x}_m \\
| & | & & |
\end{bmatrix}\\\\
\boldsymbol{X}'&=
\begin{bmatrix}
| & | & & | \\
\boldsymbol{x}_2 & \boldsymbol{x}_3 & \cdots & \boldsymbol{x}_{m+1} \\
| & | & & |
\end{bmatrix}
\end{align}

つまり、 $\boldsymbol{X}$ は行列 $\boldsymbol{A}$ の反復で、

\boldsymbol{X}\simeq
\begin{bmatrix}
| & | & & | \\
\boldsymbol{x}_1 & \boldsymbol{A}\boldsymbol{x}_1 & \cdots & \boldsymbol{A}^{m-1}\boldsymbol{x}_1 \\
| & | & & |
\end{bmatrix}

と近似で表現できる。
ここで、各列がクリロフ部分空間（c.f.Wikipedia）に属することに注目する。行列 $\boldsymbol{X}'$ は $\boldsymbol{X}$ をシフト演算した形で表される。

\begin{align}
\boldsymbol{X}'&=\boldsymbol{XS} \\
\boldsymbol{S}&:=
\begin{bmatrix}
0 & 0 & \cdots & 0 & a_1 \\
1 & 0 & \cdots & 0 & a_2 \\
0 & 1 & \cdots & 0 & a_3 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & \cdots & 1 & a_m \\
\end{bmatrix}
\end{align}

この行列 $\boldsymbol{S}$ はコンパニオン行列と呼ばれ、左 $m-1$ 列は列のシフト、一番右の列は残差を最小化する係数が与えられている。
このように、当初のDMDアルゴリズムはアーノルディ法（固有値計算反復アルゴリズム）とよく似ていることが分かる。実際に、 $\boldsymbol{X}=\left(\boldsymbol{x}_1\ \boldsymbol{x}_2\ \cdots\ \boldsymbol{x}_m\right)$ はクリロフ部分空間 $\mathcal{K}_m(\boldsymbol{A},\boldsymbol{x}_1)$ を構成する列ベクトルからなる行列であり、これを列正規化したものを $\boldsymbol{Q}$ とすると、

\begin{align}
&\boldsymbol{Q}=\left(\frac{\boldsymbol{x}_1}{\|\boldsymbol{x}_1\|}\ \frac{\boldsymbol{x}_2}{\|\boldsymbol{x}_2\|}\  \cdots\ \frac{\boldsymbol{x}_m}{\|\boldsymbol{x}_m\|}\right) \\
\Rightarrow &\boldsymbol{S}\simeq\boldsymbol{Q}^*\boldsymbol{A}\boldsymbol{Q} \\
\Rightarrow &\boldsymbol{Q}\boldsymbol{S}\simeq\boldsymbol{A}\boldsymbol{Q}
\end{align}

ここで、 $\boldsymbol{S}$ の固有値を $\lambda$ 、固有ベクトルを $\boldsymbol{v}$ 、誤差項を $\boldsymbol{D}$ として、

\begin{align}
&\boldsymbol{Q}\boldsymbol{S}\simeq\boldsymbol{A}\boldsymbol{Q} \\
\Rightarrow&\boldsymbol{Q}\boldsymbol{S}+\boldsymbol{D}=\boldsymbol{A}\boldsymbol{Q} \\
\Rightarrow&\boldsymbol{Q}\boldsymbol{S}\boldsymbol{v}+\boldsymbol{D}\boldsymbol{v}=\boldsymbol{A}\boldsymbol{Q}\boldsymbol{v} \\
\Rightarrow&\lambda\boldsymbol{Q}\boldsymbol{v}+\boldsymbol{D}\boldsymbol{v}=\boldsymbol{A}\boldsymbol{Q}\boldsymbol{v} \\
\Rightarrow&\boldsymbol{D}\boldsymbol{v}=\left(\boldsymbol{A}-\lambda\boldsymbol{E}\right)\boldsymbol{Q}\boldsymbol{v} \\
\end{align}

誤差 $\boldsymbol{D}\rightarrow\boldsymbol{O}$ の時、 $\boldsymbol{A}-\lambda\boldsymbol{E}\rightarrow\boldsymbol{O}$ なので、 $\boldsymbol{S}$ と $\boldsymbol{A}$ の固有値は共有されることになる。したがって、行列 $\boldsymbol{S}$ のスペクトル分解をすることでDMDが実現できるのだが、先ほど紹介したexact DMDアルゴリズムの方が数値計算的に優れている。

特異値分解とスペクトル展開

DMDの重要なポイントは、データドリブンなスペクトル分解という観点からシステム状態を展開できることだ。
$\boldsymbol{\phi}_j$ をDMDモード（行列 $\boldsymbol{A}$ の固有ベクトル）、 $\lambda_j$ をDMD固有値（行列 $\boldsymbol{A}$ の固有値）として、

\begin{align}
\boldsymbol{x}_k&=\boldsymbol{A}^{k-1}\boldsymbol{x}_1 \\
&=\boldsymbol{\Phi\Lambda}^{k-1}\boldsymbol{\Phi}^\dagger\boldsymbol{x}_1
\end{align}

ここで、モード振幅 $b_j$ を $\left(b_0\ b_1\cdots b_r\right)=\boldsymbol{\Phi}^\dagger\boldsymbol{x}_1$ を満足するものと置けば、

\begin{align}
\boldsymbol{x}_k&=\boldsymbol{\Phi}\boldsymbol{\Lambda}^{k-1}\boldsymbol{b}　 \\
&=
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
\lambda_1^{k-1} & & \\
& \ddots & \\
& & \lambda_r^{k-1}
\end{bmatrix}
\begin{bmatrix}
b_1 \\
\vdots \\
b_r
\end{bmatrix} \\
&=\sum_{j=1}^r \boldsymbol{\phi}_j\lambda_j^{k-1}b_j
\end{align}

参考書では、

\boldsymbol{x}_k=\boldsymbol{\Phi}\boldsymbol{\Lambda}^{k-1}\boldsymbol{b}=
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
\lambda_1 & & \\
& \ddots & \\
& & \lambda_r
\end{bmatrix}
\begin{bmatrix}
b_1 \\
\vdots \\
b_r
\end{bmatrix}

とされているが、固有行列の指数が抜けている気がする。

と各モード $\boldsymbol{x}_k$ を特異値分解することができる。
さらに、このDMDスペクトル展開は以下のように式変形可能

\begin{align}
\boldsymbol{x}_k&=
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
b_1 & & \\
& \ddots & \\
& & b_r
\end{bmatrix}
\begin{bmatrix}
\lambda_1^{k-1} \\
\vdots \\
\lambda_r^{k-1}
\end{bmatrix} \\
\Rightarrow
\boldsymbol{X}&=
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
b_1 & & \\
& \ddots & \\
& & b_r
\end{bmatrix}
\begin{bmatrix}
\lambda_1 & \cdots & \lambda_1^{m-1} \\
\vdots & \ddots & \vdots \\
\lambda_r & \cdots & \lambda_r^{m-1}
\end{bmatrix}
\end{align}

モード振幅 $\boldsymbol{b}$ は最初のスナップショット $\boldsymbol{x}_1$ を使ってその混合を決定するのだが、 $\boldsymbol{b}=\boldsymbol{\Phi}^\dagger\boldsymbol{x}_1$ という簡単な定義式を用いても計算コストがかなり高くなってしまう。
そこで、projected modes同様に縮約モデルを用いた計算コスト軽減を図る。

\begin{align}
&&\boldsymbol{x}_1&=\boldsymbol{\Phi b} \\
&\Rightarrow&\tilde{\boldsymbol{U}}\tilde{\boldsymbol{x}}_1&=\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{Wb} \\
&\Rightarrow&\tilde{\boldsymbol{x}}_1&=\tilde{\boldsymbol{U}}^*\boldsymbol{X}'\tilde{\boldsymbol{V}}\tilde{\boldsymbol{\Sigma}}^{-1}\boldsymbol{Wb} \\
&\Rightarrow&\tilde{\boldsymbol{x}}_1&=\tilde{\boldsymbol{A}}\boldsymbol{Wb} \\
&\Rightarrow&\tilde{\boldsymbol{x}}_1&=\boldsymbol{W\Lambda b} \\
&\Rightarrow&\boldsymbol{b}&=\left(\boldsymbol{W\Lambda}\right)^{-1}\tilde{\boldsymbol{x}}_1 \\
\end{align}

元の固有ベクトル行列 $\boldsymbol{\Phi}\in\mathbb{R}^{n\times r}$ と比較して、行列 $\boldsymbol{W}$ と $\boldsymbol{\Lambda}$ はいずれも $\mathbb{R}^{r\times r}$ に属しており、軽量化されていることが分かる。

上記の特異値展開は、連続固有値 $\omega=\log{(\lambda)/\Delta t}$ を導入することによって、連続時間でも記述できる。

この離散時間系 $\lambda $ と連続時間系 $ \omega$ のDMD固有値の関係：

e^{\omega\Delta t} = \lambda,
\,i.e.
\quad
\omega = \frac{\log{\lambda}}{\Delta t}

これは、クープマン固有値とリー固有値の関係と同じである。詳細はこちらの記事を参照

\boldsymbol{x}(t)=\sum_{j=1}^r\boldsymbol{\phi}_je^{\omega_j t}b_j=\boldsymbol{\Phi}e^{\boldsymbol{\Omega}t}\boldsymbol{b}

ここで、 $\boldsymbol{\Omega}$ は連続系の固有値 $\omega_j$ を対角成分に持つ対角行列であり、データ行列 $\boldsymbol{X}$ はVandermonde行列 $\boldsymbol{T}(\boldsymbol{\omega})$ を用いて以下のように表現できる。

\boldsymbol{X}\simeq
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
b_1 & & \\
& \ddots & \\
& & b_r
\end{bmatrix}
\begin{bmatrix}
e^{\omega_1t_1} & \cdots & e^{\omega_1t_m} \\
\vdots & \ddots & \vdots \\
e^{\omega_rt_1} & \cdots & e^{\omega_rt_m}
\end{bmatrix}
=\boldsymbol{\Phi}\text{diag}(\boldsymbol{b})\boldsymbol{T}(\boldsymbol{\omega})

コーディング例

本章では、DMDのプログラム実装を行う。
シミュレーションデータはIBPMで作成された、二次元円柱周りの流れ場データを用いる。データはこちらから取得可能。

環境

• 言語: python3.12
• OS: macOS Sonoma14.5
• RAM: 64GB

データ読み込み

Jupyterで書いたので、セル別に区切って掲載する。

import matplotlib.animation as animation
import matplotlib.colors as mcolors
import matplotlib.pyplot as plt
import numpy as np
from scipy import io
from scipy.signal import periodogram

vortall_mat = io.loadmat('../DMD/FLUIDS/CYLINDER_ALL.mat')
X = vortall_mat['VORTALL']
time_steps = X.shape[1]
width = 199
height = 449

FLUIDSというディレクトリ傘下にCYLINDER_ALL.matというMatlab配列のデータがあるので、それを読み取りに行く。以下は必要ないのだが、vortall_mat.keys()でキーを確認すると、'UALL', 'UEXTRA', 'VALL', 'VEXTRA', 'VORTALL', 'VORTEXTRA'があることが分かる。末尾がEXTRAのものはデータ数が1でALLは151あるので、（推測だが）EXTRAは時系列的に一単位時間未来のデータなのだろう。今回は'VORTALL'を使う。

シミュレーションデータの可視化

DMDをする前に、まずは元のシミュレーションデータの可視化をしたくなる。Matplotlibには様々なカラーマップが用意されているが、離散で配色がグラデーションとなっているものがないので、カスタムで作成する。

cmap = mcolors.ListedColormap([
    '#67001f', '#7f1825', '#98312b', '#b2182b', '#ca3a4b',
    '#d6604d', '#e78a70', '#f4a582', '#fddbc7', '#fbf0ef',
    '#f7f7f7', '#d1e5f0', '#b1cfe9', '#92c5de', '#6d9bc4',
    '#4393c3', '#2c7bae', '#2166ac', '#174a88', '#053061'
])

このカラーマップを用いてアニメーションを作成

# Animation of the original data
fig, ax = plt.subplots(figsize=(2.5, 4))
im = ax.imshow(
    X[:,0].reshape(height, width),
    cmap=cmap,
    norm=mcolors.Normalize(vmin=-3., vmax=3.),
    interpolation='nearest'
)
plt.colorbar(im, ax=ax)

# Update function for animation
def update(frame):
    im.set_array(X[:,frame].reshape(height, width))
    return [im]

ani = animation.FuncAnimation(
    fig,
    update,
    frames=range(time_steps),
    blit=True,
    interval=50
)
ani.save('flow_field_animation.gif', writer='imagemagick')

すると、以下のような.GIFが作成される。

DMDアルゴリズムの実装

先述したexact DMDの記述に倣って関数を作成する。
コメントアウトがある段落はアルゴリズムの各stepに対応している。

def dmd(X, rank, exact = True):
    # Split into _X and Xprime
    Xprime, _X = X[:, 1:], X[:, :-1]
    
    # Compute the SVD of X
    U, S, Vh = np.linalg.svd(_X, full_matrices=False)
    Ur = U[:,:rank]
    Sr = np.diag(S[:rank])
    Vhr = Vh[:rank, :]

    # Obtain Atilde by computing the pseudo-inverse of X
    Atilde = np.linalg.solve(Sr, (Ur.T @ Xprime @ Vhr.T))

    # The Spectral decomposition of Atilde
    eigs, W = np.linalg.eig(Atilde)

    # Reconstructed the high-demensional DMD modes
    Phi = Xprime @ np.linalg.solve(Sr.T, Vhr).T @ W @ np.diag(1 / eigs) if exact else Ur @ W
    x1tilde = Sr @ Vhr[:,0]
    b = np.linalg.solve(W @ np.diag(eigs), x1tilde)
    return Phi, eigs, b

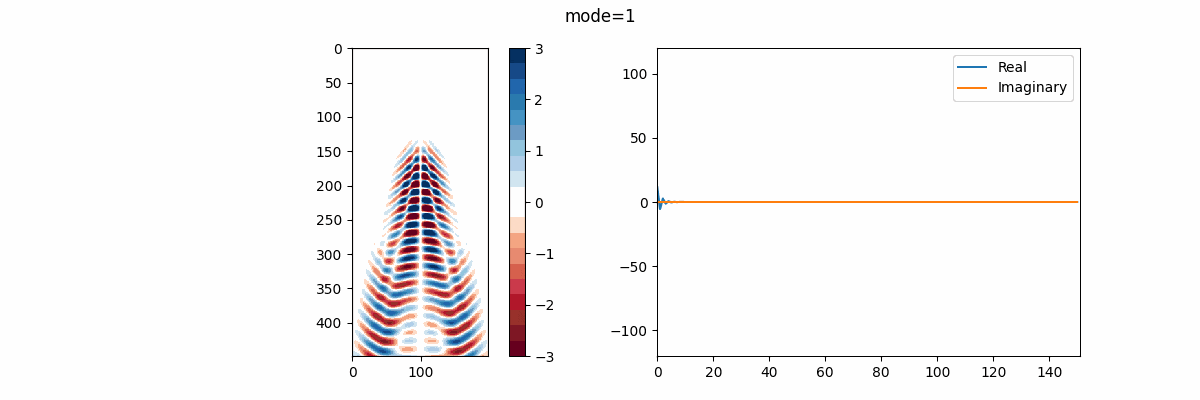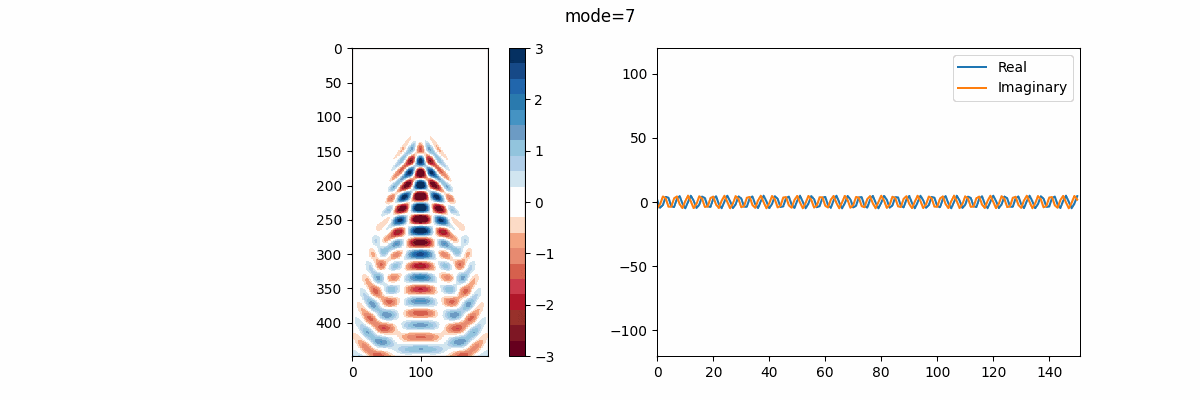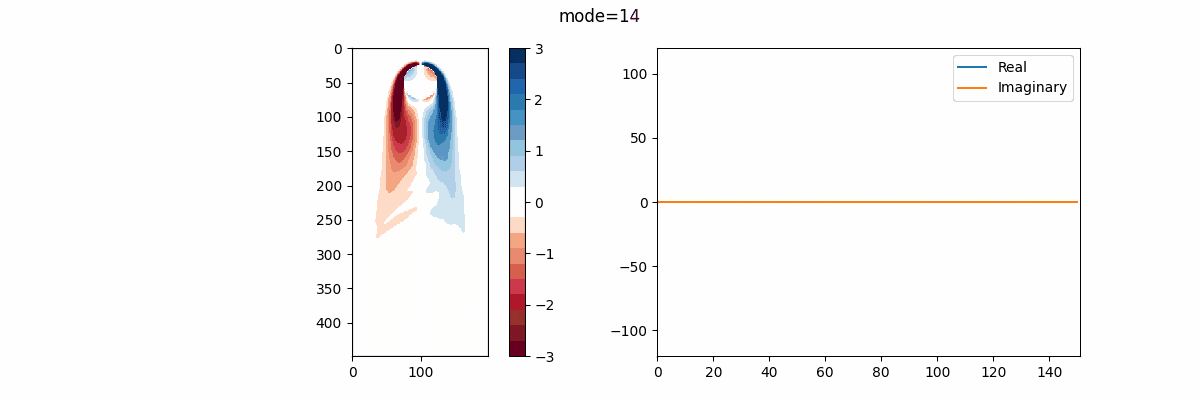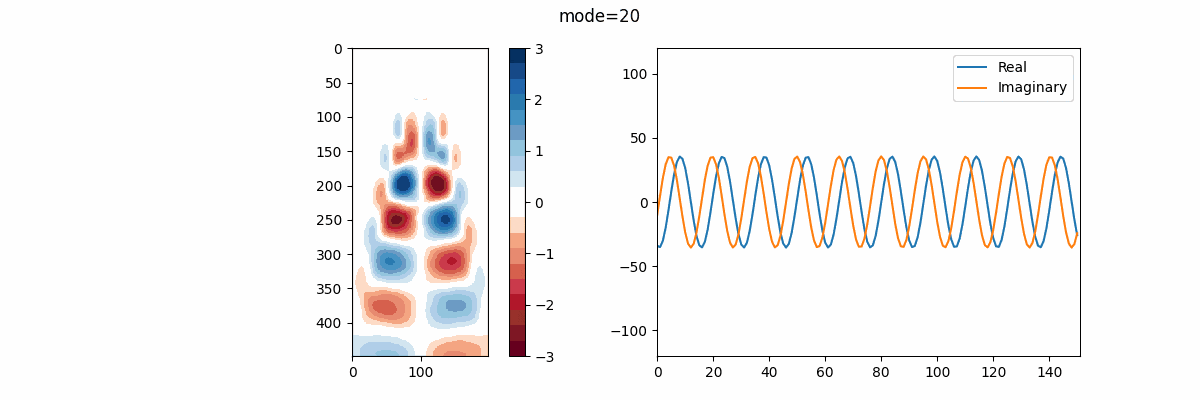
そして、この関数を呼び出した結果を用いて（今回は $rank=20$ ）①DMDモード、②振動周波数を並べたアニメーションを作成。この振動周波数 $f$ は、次のように与えられる：

f = \frac{\Im{\omega}}{2\pi}

$\Im{\omega}$ は $ \omega$ の虚部を示す。

ここで、振動周波数に離散固有値 $\lambda $ ではなく、連続固有値 $ \omega$ を用いる理由は、離散固有値は次元を持たず、物理的な意味を持ちにくい一方で、連続時間の周波数は"ヘルツ"として解釈しやすい為である。

# Animation of the DMD modes (Diagnostics)
vmax = 10**-2
R = 20
Phi, eigs, b = dmd(X, R)

# Plot DMD modes
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
im1 = ax1.imshow(
    Phi[:,0].real.reshape(height, width),
    cmap=cmap,
    norm=mcolors.Normalize(vmin=-vmax, vmax=vmax),
    interpolation='nearest'
)
plt.colorbar(im, ax=ax1)

# ax2 customize
ax2.set_xlim(0, time_steps)
ax2.set_ylim(-120, 120)

# Plot oscillation frequencies
omega = np.log(eigs)
time_dynamics = np.zeros((len(b), time_steps), dtype='complex')
for t in range(time_steps):
    time_dynamics[:,t] = np.diag(b) @ np.exp(omega * t).T
line_real, = ax2.plot(np.arange(time_steps), time_dynamics[0].real, label='Real')
line_imag, = ax2.plot(np.arange(time_steps), time_dynamics[0].imag, label='Imaginary')

# Update function
def update(frame):
    im1.set_array(Phi[:,frame].real.reshape(height, width))
    im1.set_norm(mcolors.Normalize(vmin=-vmax, vmax=vmax))
    line_real.set_ydata(time_dynamics[frame].real)
    line_imag.set_ydata(time_dynamics[frame].imag)
    ax2.legend(loc='upper right')
    fig.suptitle(f"mode={frame+1}")
    return [im1, line_real, line_imag]

ani = animation.FuncAnimation(
    fig,
    update,
    frames=range(R),
    blit=True,
    interval=400
)
ani.save('mode_real_animation.gif', writer='imagemagick')

実行結果は以下のようになる。

実部を青線、虚部を橙線で示しているが、改めて述べると、実部はモードの成長率または減衰率、虚部はモードの振動周波数を表す。 故に、この結果を見ればモード17,18がシステム内でとりわけ大きなエネルギーを持っていると解釈できる。

システムの再構築

今度は逆に、DMDの結果を用いて系自体を再構築してみる。先述してはいるが、数学的に以下の操作を行うことになる。

\boldsymbol{X}\simeq
\begin{bmatrix}
| & & | \\
\boldsymbol{\phi}_1 & \cdots & \boldsymbol{\phi}_r \\
| & & |
\end{bmatrix}
\begin{bmatrix}
b_1 & & \\
& \ddots & \\
& & b_r
\end{bmatrix}
\begin{bmatrix}
e^{\omega_1t_1} & \cdots & e^{\omega_1t_m} \\
\vdots & \ddots & \vdots \\
e^{\omega_rt_1} & \cdots & e^{\omega_rt_m}
\end{bmatrix}
=\boldsymbol{\Phi}\text{diag}(\boldsymbol{b})\boldsymbol{T}(\boldsymbol{\omega})

連続固有値 $\omega$ とタイムステップ $\lbrace t_i\rbrace$ からVandermonde行列を生成する関数を作る。

def vandermonde(mu, ts):
    mu = mu.reshape(-1, 1)
    ts = ts.reshape(1, -1)
    lnV = mu @ ts
    V = np.exp(lnV)
    return V, lnV

これを用いて、全ての時刻 $\lbrace t_i\rbrace$ の状態を復元する。

# Reconstruct X
ts = np.arange(X.shape[1])
omega = np.log(eigs)
V, _ = vandermonde(eigs, ts)
Xr = Phi @ np.diag(b) @ V

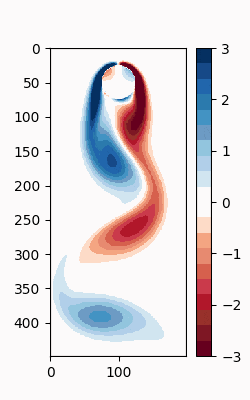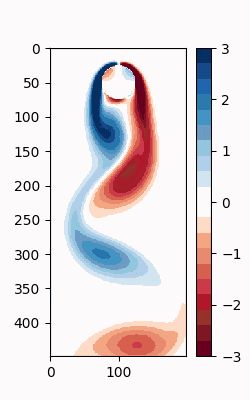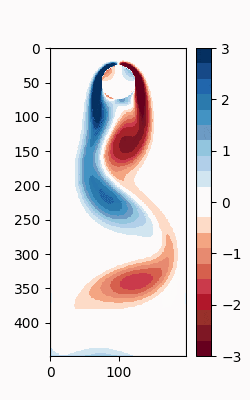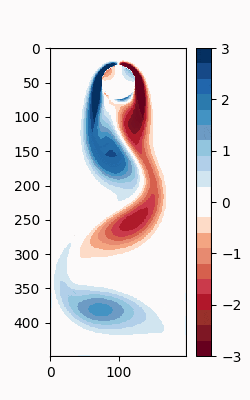
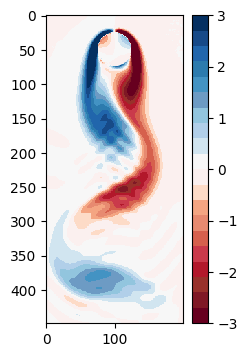
例えば、一番最初の時刻 $t_1$ を描画してみると以下のようになる。

### Display the reconstructed data
fig, ax = plt.subplots(figsize=(2.5, 4))
im = ax.imshow(
    Xr[:,0].real.reshape(height, width),
    cmap=cmap,
    norm=mcolors.Normalize(vmin=-3., vmax=3.),
    interpolation='nearest'
)
plt.colorbar(im, ax=ax)

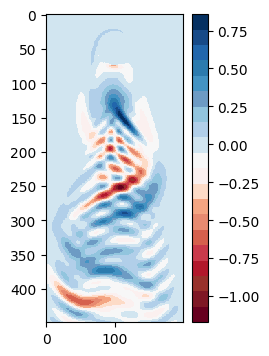
元のシミュレーションデータの時刻 $t_0$ との差分を取ってみて、誤差を視覚化してみる。

# Display the difference between original and reconstructed data
fig, ax = plt.subplots(figsize=(2.5, 4))
im = ax.imshow(
    (Xr[:,0].real-X[:,0]).reshape(height, width),
    cmap=cmap,
    interpolation='nearest'
)
plt.colorbar(im, ax=ax)

復元誤差を可視化しても定量的には評価できないので、以下のフロベニウスノルムを用いた相対誤差で評価する。

\text{appx. ratio}:=\frac{\|\boldsymbol{X}-\boldsymbol{\Phi}\text{diag}(\boldsymbol{b})\boldsymbol{T}(\boldsymbol{\omega})\|_F}{\|\boldsymbol{X}\|_F}

num = np.linalg.norm((Xr[:, 0].real - X[:, 0]).reshape(height, width), "fro")
den = np.linalg.norm(X[:, 0].reshape(height, width), "fro")
num * 100 / den

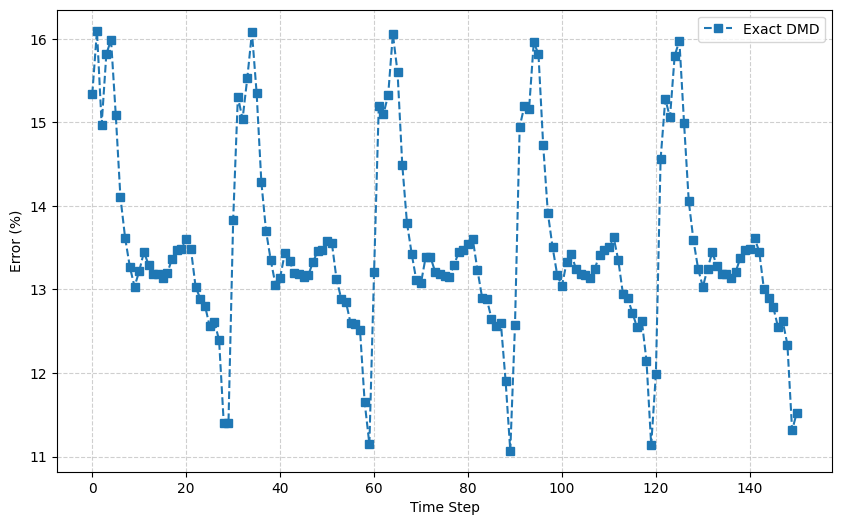
この結果として時刻 $t_1$ に対し、復元誤差15.3%を得る。これを全ての時刻に対して実施し、プロットすると以下の様になる。

# Measure the accuracy of the reconstruction
def measure_columnwise_accuracy(func, *args, **kwargs):
    _Phi, _eigs, _ = func(*args, **kwargs)
    _omega = np.log(_eigs)
    _V, _ = vandermonde(_omega, ts)
    _Xr = _Phi @ np.diag(b) @ _V
    return np.linalg.norm(X - _Xr.real, axis=0) * 100 / np.linalg.norm(X, axis=0)

# Plot the errors 
exact_errors = measure_columnwise_accuracy(dmd, X, R, exact=True)
plt.figure(figsize=(10, 6))
plt.plot(ts, exact_errors, label="Exact DMD", marker="s", linestyle="--")

# Customize the plot
plt.xlabel("Time Step")
plt.ylabel("Error (%)")
plt.legend()
plt.grid(True, linestyle="--", alpha=0.6)

# Show the plot
plt.show()

この描画結果から分かるように、時間ごとの誤差には周期性が見られる。これは、DMDモードが主に特定の振動周波数（たとえばStrouhal数に対応する周波数）を含んで再構成されるためである。その結果、元データに含まれない周波数成分が再構成に混入したり、位相のずれが生じたりすることで、誤差が周期的に増減し、誤差の時間変化に周期性が現れると解釈できる。

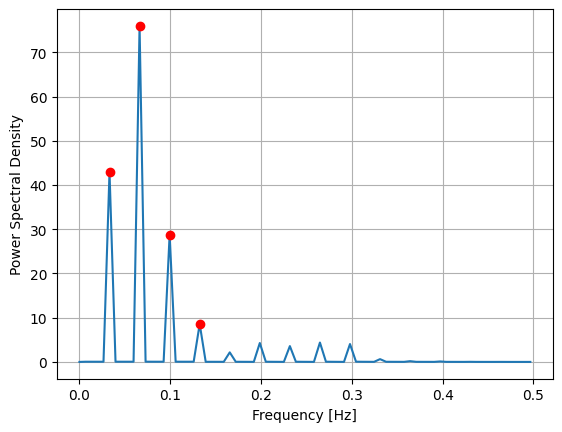
例えば、ここで誤差時系列に対し、パワースペクトル密度を求めてみると、

# Frequency analysis
fs = 1
freqs, psd = periodogram(exact_errors, fs=fs, scaling="density")
peaks, properties = find_peaks(psd, height=psd.max() * 0.1)  # Extract the top 10% or more

# Dominant frequency
dominant_freqs = freqs[peaks]
dominant_powers = properties["peak_heights"]
sorted_idx = np.argsort(dominant_powers)[::-1]

# Results (Standard output)
print("支配的な周波数 (Hz) と対応する周期:")
for i in sorted_idx:
    f = dominant_freqs[i]
    print(f"  - 周波数: {f:.4f} Hz  → 周期 ≈ {1/f:.2f}")

# Plot
plt.plot(freqs, psd)
plt.plot(freqs[peaks], psd[peaks], "ro")
plt.xlabel("Frequency [Hz]")
plt.ylabel("Power Spectral Density")
plt.grid(True)
plt.show()

[出力結果]

支配的な周波数 (Hz) と対応する周期:
  - 周波数: 0.0662 Hz  → 周期 ≈ 15.10
  - 周波数: 0.0331 Hz  → 周期 ≈ 30.20
  - 周波数: 0.0993 Hz  → 周期 ≈ 10.07
  - 周波数: 0.1325 Hz  → 周期 ≈ 7.55

この結果から周波数0.0662Hzと0.0331Hzが特に復元誤差へ支配的な影響力を持っていることがわかった。

さらに、Exact DMDの結果から各モードの周波数を出力してみる。

print("=" * 70)
print(f"{'Index':<6}{'絶対固有値':<12}{'周波数 (Hz)':<12}{'モード振幅':<15}")
print("-" * 70)
omegas = np.log(eigs)
frequencies = np.imag(omegas) / (2 * np.pi)
for i, (eig, freq, amp) in enumerate(zip(np.abs(eigs), frequencies, np.abs(b))):
    print(f"{i+1:<6}{eig.item():<15.6f}{freq.item():<15.6f}{amp.item():<15.6f}")
print("=" * 70)

[出力結果]

======================================================================
Index 絶対固有値       周波数 (Hz)    モード振幅          
----------------------------------------------------------------------
1     0.484637       0.500000       11.584380      
2     1.000002       0.297733       4.944648       
3     1.000002       -0.297733      4.944648       
4     1.000030       0.264640       5.014162       
5     1.000030       -0.264640      5.014162       
6     0.999991       0.231557       4.911871       
7     0.999991       -0.231557      4.911871       
8     0.999994       0.198477       4.950382       
9     0.999994       -0.198477      4.950382       
10    1.000002       0.165397       6.261412       
11    1.000002       -0.165397      6.261412       
12    1.000001       0.132317       10.062394      
13    1.000001       -0.132317      10.062394      
14    1.000000       0.000000       291.541446     
15    1.000000       0.099238       27.193561      
16    1.000000       -0.099238      27.193561      
17    1.000000       0.033079       102.287304     
18    1.000000       -0.033079      102.287304     
19    1.000000       0.066158       35.525853      
20    1.000000       -0.066158      35.525853      
======================================================================

先ほどのパワースペクトル密度の結果から、周波数0.0662Hzと0.0331Hzが支配的であることが判明したが、それぞれ（共役複素数なので対になるモードがあり）モード19,20とモード17,18が対応していると分かる。

DMDの復元誤差の減少を図った戦略はいくつかあるが本稿では割愛する。

exact DMD VS standard DMD

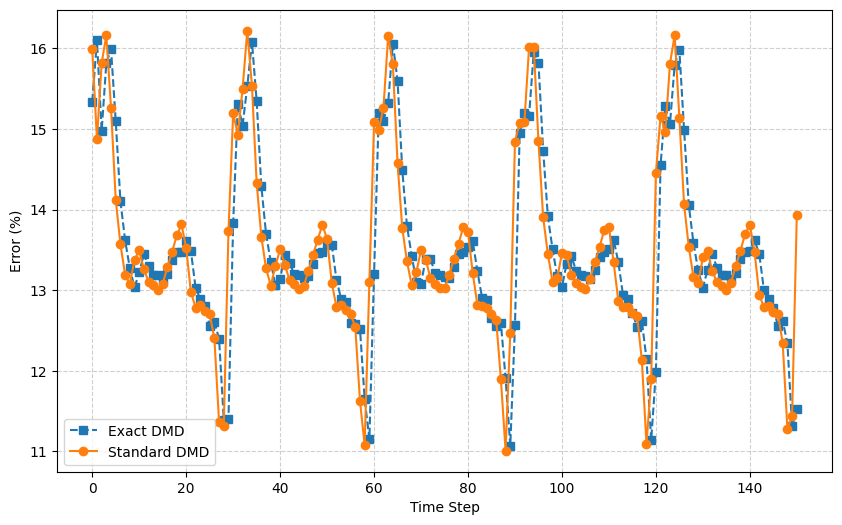
先に述べたように、Exact DMDは計算コストを上げてでも数学的厳密性を重視した手法である。一方、Standard DMDは最後のスナップショットを用いてコンパニオン行列を構成し、そこからモードを抽出するため、特定時刻の復元精度に偏りが生じやすい。実際、下図に示すように、時間 t=150 ではStandard DMDの復元誤差が大きく跳ね上がっており（13.9%）、これはその時刻の状態 $\boldsymbol{x}_{t=150}$ がStandard DMDのモード空間から外れているためと解釈できる。

一方、Exact DMDは初期状態 $\boldsymbol{x}_{t=0}$ を列空間に持たないにもかかわらず、再構成誤差は比較的小さく（11.5%）抑えられている。これは、Exact DMDがスナップショット全体の構造を反映したモードを構成しており、特定時刻に依存しない安定した再構成性能を持つことを示している。

この比較から、Standard DMDはコンパニオン行列の構造上、末尾の状態再構成に有利だが、時系列全体の再現性には劣る。一方、Exact DMDは計算コストを伴うが、より堅牢で安定したモード抽出が可能であり、時間全体にわたる復元精度の観点では優位性があると言える。

固有値のプロット

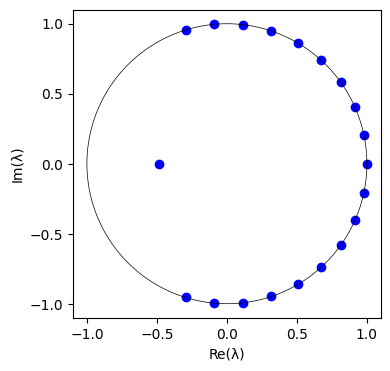
最後の検証として、固有値 $\lambda_j$ の複素平面へのプロットを行う。

# Plot eigenvalues on complex plane
re = eigs.real
im = eigs.imag
plt.figure(figsize=(4,4))
plt.scatter(re, im, color='blue', marker='o')

# Add an unit circle
theta = np.linspace(0, 2*np.pi, 300)
x = np.cos(theta)
y = np.sin(theta)
plt.plot(x, y, 'k-', linewidth=0.5)

plt.gca().set_aspect('equal', adjustable='box')
plt.xticks(np.arange(-1, 1.5, 0.5))
plt.yticks(np.arange(-1, 1.5, 0.5))
plt.xlabel('Re(λ)')
plt.ylabel('Im(λ)')
plt.show()

結果は以下の通り。

ほとんどの固有値が単位円上に固有値が並んでいることが分かる。
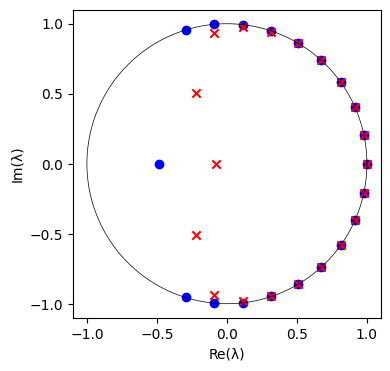
DMDは実験データ、数値データどちらにも適用可能であるが、ノイズの多いデータに対しては敏感であることが知られている。そこで、元のデータに $10^{-1}$ 程度のガウシアンノイズを加えて、再度プロットしてみる。

# Added Gaussian noise
noise = np.random.normal(0, 10**-1, X.shape)
X_gn = X + noise
Phi_gn, Lambda_gn, b_gn = dmd(X_gn, 21)

このように、ノイズが加えられたデータのDMD固有値は不規則に配置される。

おわりに

今回はexact DMDのアルゴリズムを理解して、二次元円柱周りの流れ場データを使って実際にDMDを適用させてみた。参考書にはDMDの派生や近似手法などの紹介もあったので、実際にそれらの手法も試してみたいと思う。