これはR言語 Advent Calendar 2025の、7日目の記事です。
データ分析において、複数の変数間の複雑な関係性を探ることは非常に重要です。この記事では、多変量正規分布に従う変数間の関係をモデル化する2つの強力な手法、ガウシアン・グラフィカル・モデリング(GGM, Gaussian
Graphical Modeling) とガウシアン・ベイジアン・ネットワーク(GBN, Gaussian Bayesian
Network) について、Rを使った実践的なコード例とともに解説します。
グラフモデルの役割とGGM vs GBN
グラフィカルモデルは、変数(ノード)とそれらの関係性(エッジ)をグラフとして表現する統計モデルです。
1. ガウシアン・グラフィカル・モデリング(GGM)
GGMは、変数間の条件付き独立性、つまり「他のすべての変数を固定したときに、2つの変数に直接的な相関があるか」を推定します。
- エッジの意味: 変数間のつながりの有無(無向グラフ)。エッジの重みは偏相関係数で表されます。
- 古典的手法: 統計的仮説検定($\text{p}$値)に基づいて、偏相関係数がゼロでないかを判断します。
- 現代的手法: グラフィカル・ラッソ(Graphical Lasso)。罰則項(Lasso)を導入することで、スパースな(エッジの少ない)グラフ構造を推定し、特に高次元データで有効性が増します。
2. ガウシアン・ベイジアン・ネットワーク(GBN)
GBNは、変数間の因果関係を確率的に記述するモデルです。
-
エッジの意味: 変数間の因果の方向(有向非巡回グラフ:DAG, Directed
Acyclic Graph)。$X \to Y$ のエッジは、$Y$が$X$に依存していることを示します。 - モデルの構成: DAGに基づき、各変数を親ノード(原因)からの線形回帰モデルとして表現します。これにより、複雑な因果構造を推論できます。
共通点: どちらも変数が多変量正規分布に従うことを前提としています。
Rでの実践:5教科の点数データ分析
RのパッケージqgraphでGGM、bnlearnでGBNを実行してみましょう。
if (!require("pacman")) install.packages("pacman")
pacman::p_load(
conflicted,
tidyverse,
qgraph, # グラフィカルモデリング
bnlearn, # ベイジアンネットワーク
Rgraphviz
)
データの準備
5つの数学系教科の試験の点数データmarksを使用します。
data(marks)
head(marks)
| 変数名 | 教科名 |
|---|---|
| MECH | 力学 |
| VECT | 微分・積分 |
| ALG | 代数学 |
| ANL | 解析学 |
| STAT | 統計学 |
1. GGMによる変数間の「つながり」の推定
統計的仮説検定に基づくGGM
古典的なGGMでの実行例です。
marks_cor <- marks |>
cor()
res_pcor <- marks_cor |>
qgraph(
graph = "pcor",
alpha = 0.05,
minimum = "sig",
threshold = "holm",
sampleSize = nrow(marks),
theme = "colorblind", # 配色テーマ
title = "古典的GGM",
layout = "spring"
)
GGMのエッジの重みは偏相関係数になっています。
res_pcor |>
getWmat() |>
round(3)
# MEC VEC ALG ANL STA
# MEC 0.000 0.329 0.000 0.000 0.000
# VEC 0.329 0.000 0.000 0.000 0.000
# ALG 0.000 0.000 0.000 0.432 0.357
# ANL 0.000 0.000 0.432 0.000 0.000
# STA 0.000 0.000 0.357 0.000 0.000
グラフィカル・ラッソによるGGM
古典的なGGMより精度の高いグラフィカル・ラッソを使って、試験の点数間の直接的な関連性を可視化します。
marks_cor <- marks |>
cor()
res_glasso <- marks_cor |>
qgraph(
graph = "glasso",
sampleSize = nrow(marks),
threshold = TRUE,
theme = "colorblind",
title = "グラフィカル・ラッソによるGGM",
layout = "spring"
)
このグラフのエッジ(線)が存在する場合、他の教科の点数の影響を排除しても、その2教科の点数間に直接的な関連(偏相関)があることを示します。
偏相関係数(エッジの重み) を確認してみましょう。
res_glasso |>
getWmat() |>
round(3)
# MEC VEC ALG ANL STA
# MEC 0.000 0.327 0.229 0.000 0.000
# VEC 0.327 0.000 0.279 0.000 0.000
# ALG 0.229 0.279 0.000 0.428 0.354
# ANL 0.000 0.000 0.428 0.000 0.253
# STA 0.000 0.000 0.354 0.253 0.000
2. GBNによる「因果」構造の推定
次に、有向非巡回グラフ(DAG) を前提とし、因果の方向性を含むネットワークを推定します。
ネットワーク構造の学習
bnlearnパッケージのhill-climbing (HC) 法で最適なDAGを探索します。
# 構造学習(Structure Learning)
bn_structure <- marks |>
hc()
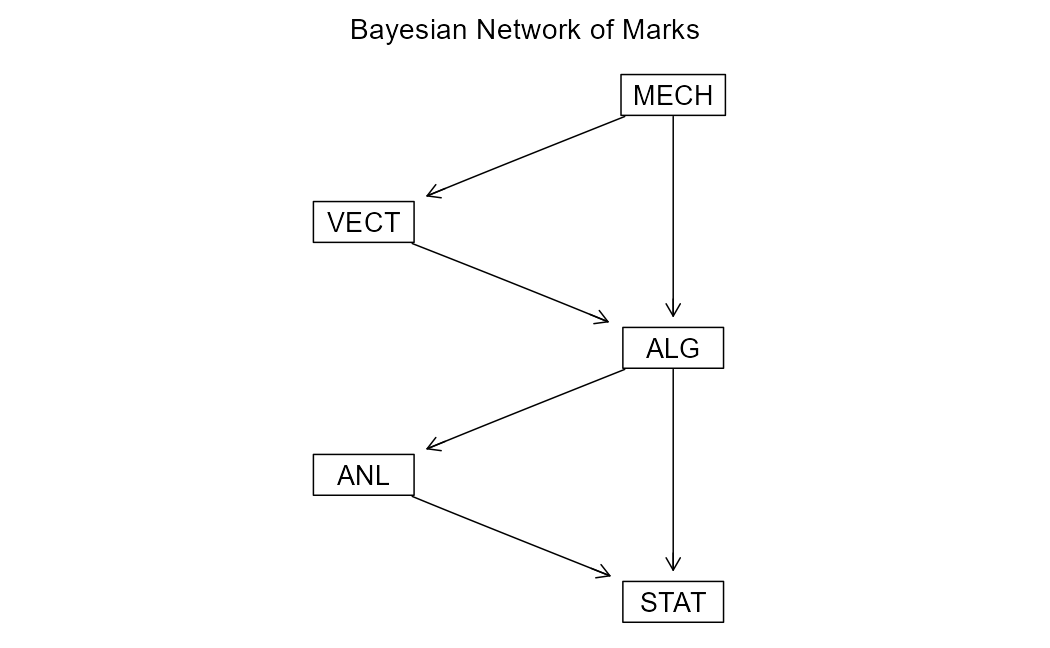
bn_structure |>
graphviz.plot(main = "Bayesian Network of Marks")
このグラフの矢印(有向エッジ)は、変数間の因果的な影響の方向を示唆します。例えば、MEC(力学)からALG(代数学)へ矢印があれば、「MEC(力学)の点数が高い(低い)ことが、ALG(代数学)の点数に影響を与えている」という解釈が可能です。
係数(回帰モデル)の推定
構造学習で決定したDAGに基づき、各ノード間の回帰係数を推定します。
bn_structure |>
bn.fit(marks)
Bayesian network parameters
# Parameters of node MECH (Gaussian distribution)
#
# Conditional density: MECH
# Coefficients:
# (Intercept)
# 38.95455
# Standard deviation of the residuals: 17.48622
#
# Parameters of node VECT (Gaussian distribution)
#
# Conditional density: VECT | MECH
# Coefficients:
# (Intercept) MECH
# 34.3828788 0.4160755
# Standard deviation of the residuals: 11.01373
#
# Parameters of node ALG (Gaussian distribution)
#
# Conditional density: ALG | MECH + VECT
# Coefficients:
# (Intercept) MECH VECT
# 25.3619809 0.1833755 0.3577122
# Standard deviation of the residuals: 8.080725
#
# Parameters of node ANL (Gaussian distribution)
#
# Conditional density: ANL | ALG
# Coefficients:
# (Intercept) ALG
# -3.574130 0.993156
# Standard deviation of the residuals: 10.50248
#
# Parameters of node STAT (Gaussian distribution)
#
# Conditional density: STAT | ALG + ANL
# Coefficients:
# (Intercept) ALG ANL
# -11.1920114 0.7653499 0.3164056
# Standard deviation of the residuals: 12.60646
出力結果は、BNを構成する各ノードの線形回帰モデルの係数を示しています。例えば、ALGのセクションを見ると、ALGが他のノードからの影響を受けているか、その影響の強さ(回帰係数)が分かります。
$$
\text{ALG} = \beta_0 + \beta_1 \cdot \text{MEC} + \beta_2 \cdot \text{VECT} + \epsilon
$$
この例でいえば以下の形になります。
$$
\text{ALG} = 25.3619809 + 0.1833755 \cdot \text{MEC} + 0.3577122 \cdot \text{VECT} + \epsilon
$$
GBNは、この回帰モデルの集合として全体の因果構造を記述しているのです。
中規模データでの比較
車の性能データmtcarsを使って、GGMとGBNの比較を試みます。
| 変数名 | 説明 |
|---|---|
| mpg | マイル/(米国)ガロン。燃費の指標。 |
| cyl | 気筒数 |
| disp | 排気量 (立方インチ) |
| hp | 総出力馬力 |
| drat | 後輪軸減速比。ドライブシャフトの回転数と車軸の回転数との比率 |
| wt | 重量 (1000ポンド) |
| qsec | 1/4マイルタイム。停止状態から約400m進むまでの時間 |
| vs | エンジン (0 = V型, 1 = 直列) |
| am | トランスミッション (0 = オートマチック, 1 = マニュアル) |
| gear | 前進ギア数 |
| carb | キャブレター数 |
統計的仮説検定に基づくGGM
mtcars_cor <- mtcars |>
cor()
res_pcor <- mtcars_cor |>
qgraph(
graph = "pcor",
alpha = 0.05,
minimum = "sig",
threshold = "holm",
sampleSize = nrow(marks),
theme = "colorblind", # 配色テーマ
title = "古典的GGM",
layout = "spring"
)
グラフィカル・ラッソによるGGM
mtcars_cor <- mtcars |>
cor()
res_glasso_mtcars <- mtcars_cor |>
qgraph(
graph = "glasso",
sampleSize = nrow(mtcars),
threshold = TRUE,
theme = "colorblind",
title = "mtcars - GGM(グラフィカル・ラッソ)",
layout = "spring"
)
GBN
mtcars_structure <- mtcars |>
hc()
mtcars_structure |>
graphviz.plot(main = "mtcars - Bayesian Network")
ん? よく見ると変な因果関係が推定されていますね。燃費mpgがキャブレター数carbに影響を与えるというのは因果関係が逆転しているようです。
こうした場合は、あり得ない因果の方向を先に指定しておくことができます。
bl <- matrix(
c(
"mpg", "carb",
"disp", "carb",
"gear", "carb",
"qsec", "carb",
"hp", "carb",
"drat", "carb",
"wt", "am",
"drat", "am",
"am", "vs",
"cyl", "vs",
"qsec", "vs"
),
ncol = 2, byrow = TRUE)
mtcars_structure <- mtcars |>
hc( blacklist = bl)
mtcars_structure |>
graphviz.plot(main = "Bayesian Network of mtcars")
まだ、おかしな因果関係が残っているかもしれませんが、いったんこのくらいで。
このように、ベイジアンネットワークのみで因果関係の方向を正しく推定することは困難で、実際にはドメイン知識に基づく修正が必要になってきます。
まとめ
| モデル | 目的 | グラフタイプ | エッジの意味 | Rでの主要パッケージ |
|---|---|---|---|---|
| GGM | 条件付き独立性の推定 | 無向グラフ | 変数間の直接的な関連性(偏相関) | qgraph |
| GBN | 確率的な因果関係の記述 | 有向非巡回グラフ (DAG) | 因果的な影響の方向(回帰係数) | bnlearn |
これらのグラフィカルモデルは、複雑な多変量データから示唆に富む構造を抽出するための強力なツールです。ぜひ皆さんのデータ分析にも活用してみてください!
Enjoy! & Merry Christmas!