【Atcoder】高校2年生でAtcoder黄色になりました

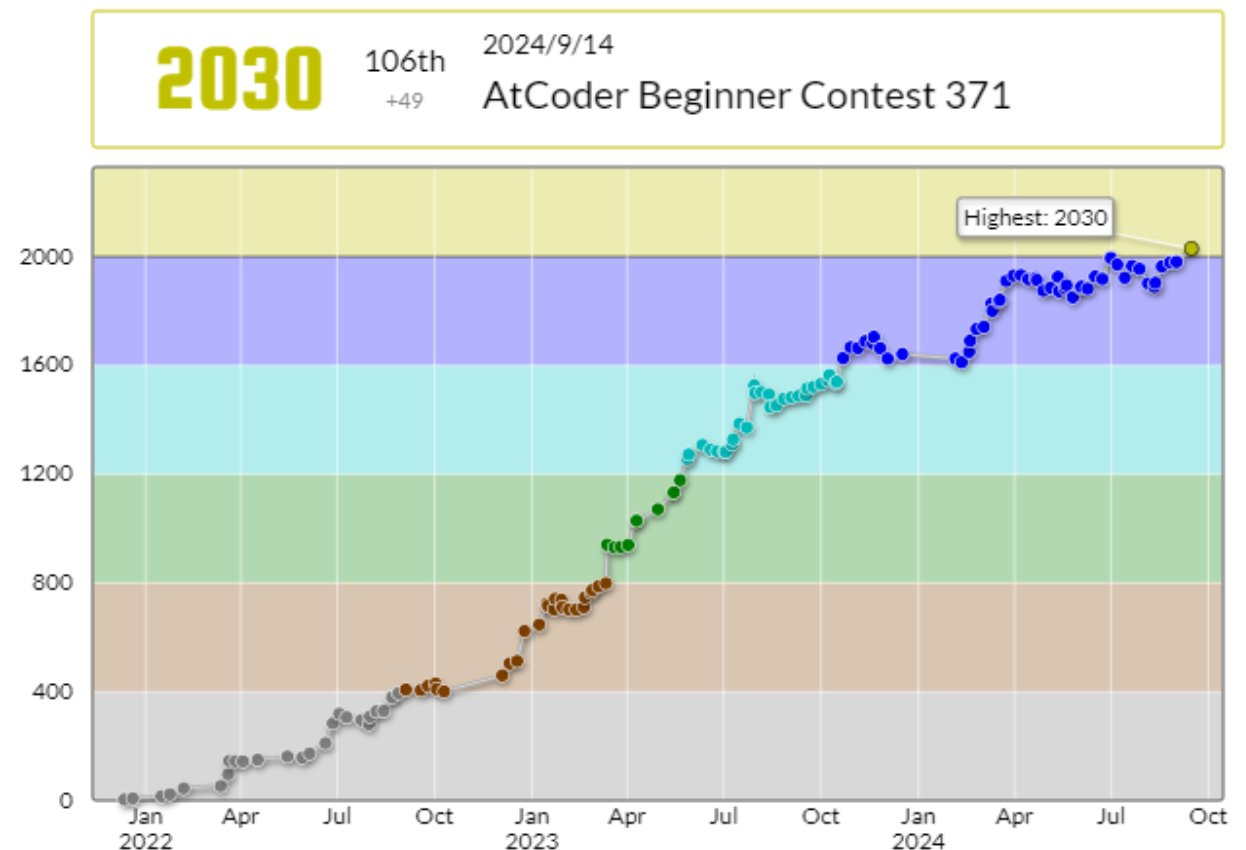
こんにちは、Blueberryです。先日行われたABC371で、念願の入黄を果たすことができました！！
とてもうれしいので記事を書きます。
なお、ARC189（Div2）にて落青し、今は黄色コーダーではなくなっています。

なお、僕のプロフィールについては過去の色変記事を参照してください。
入水記事→【Atcoder】高校1年生でAtcoder水色になりました
入水記事→【Atcoder】高校1年生でAtcoder青色になりました

AtCoderについて知らない方、各色のレベル感を知りたい方はこちらを参照してください。（AtCoder社長による色別評価です）AtCoder（競技プログラミング）の色・ランクと実力評価、問題例

※この記事は非常に長いです。お時間のあるときにどうぞ。

はじめに

レート遷移です。

2023/10/21に入青し、2024/9/14に入青しているので、約11か月で入黄したことになります。ほぼ1年ですね。長かったです！

どうやったら黄色になれるの？

青でも黄色でも、やるべきことは基本的に変わりません。競プロは練習量が強く影響してくる競技であり、精進をしないで強くなる近道はないと思います。AtCoderで黄色コーダーになるためには、ABCで安定して黄色相当のパフォーマンスを取り続ける必要があります。

現在の7問制ABCでは、6完を安定させたうえで、550点以下ぐらいのG問題は解ける必要があります。もちろんただ解ければいいというわけではなく、Gが解けない場合やGが簡単な回では早解きが重要になってきますし、そもそも序盤の問題を早く解くことができないと後半の問題のために時間を残すことができません。普段から簡潔でバグりにくい実装をする練習をしておいたり、バチャに参加して早解きの練習をしておくなどの練習は大事です。

また、ライブラリやテンプレの整備などもAtCoderで戦ううえでは重要なことですし、実行環境を整えるのも大事です。バグらせてしまうことはあるため、デバッグをしやすい環境を構築しておくのはかなり重要です。相当自分の処理能力に自信がない限り、デバッグ環境を整えることを強く推奨します。
環境構築の方法がわからない人はevimaさんの動画を参考にすると良いと思います。

基本的な実行はこの動画の範囲で行うことができますが、僕はonline-judge-toolsを使える状態にまでする方が良いと思います。サンプルをまとめて実行することができます。
なお、Windowsではない方でも、GitHub Codespaceを活用することで十分快適な環境を整えることが可能です。
僕も環境構築は慣れていませんでしたが、繰り返していくことでなんとなく把握できてきたため、どこかのタイミングで記事か動画を作成したいと思っています。

テンプレート

　僕はC++をメインで使っているので、使っているテンプレートを紹介しようと思います。C++以外の方は読み飛ばしてもらって大丈夫です。まずは全体像を貼ります。

長いので折り畳み

//コンパイル時の引数にBLUEBERRYを渡すとdeb関数が使える
#ifdef BLUEBERRY
#define deb print
// #define _GLIBCXX_DEBUG
#else
#define deb(...)
//速くなる呪文
// #pragma GCCtarget("arch=skylake-avx512")
// #pragma GCC target("avx2")
// #pragma GCC optimize("O3")
// #pragma GCC optimize("unroll-loops")
#endif

#include<bits/stdc++.h>
using namespace std;
void _main();int main(){cin.tie(0);ios::sync_with_stdio(false);cout<<fixed<<setprecision(30);_main();quick_exit(0);return 0;}
typedef long long ll;typedef long double ld;
typedef unsigned long long ull;
typedef unsigned int uint;
typedef string str;
#define rep1(a)          for(ll i = 0; i < (ll)(a); i++)
#define rep2(i, a)       for(ll i = 0; i < (ll)(a); i++)
#define rep3(i, a, b)    for(ll i = (a); i < (ll)(b); i++)
#define rep4(i, a, b, c) for(ll i = (a); i < (ll)(b); i += (c))
#define overload4(a, b, c, d, e, ...) e
#define rep(...) overload4(__VA_ARGS__, rep4, rep3, rep2, rep1)(__VA_ARGS__)
#define ALL(x) std::begin(x),std::end(x)
#define rALL(x) std::rbegin(x),std::rend(x)
#define INF ((1LL<<62)-(1LL<<31))
// #define inf ((1<<30)-(1<<15))
#define bit(x,i) (((x)>>(i))&1)
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define Endl endl
#define spa " "
#define YesNo(x) cout<<(x?"Yes":"No")<<endl;
#define YESNO(x) cout<<(x?"YES":"NO")<<endl;

#define eps (1e-8)
#define popc(x) __builtin_popcount(x)
#define crmp(x,l,r) ((l<=x)&&(x<=r))

//！？！？
#define O print
//可変長引数で入力を受け取りつつ変数を宣言
inline void scan(){}
template<class Head,class... Tail>
inline void scan(Head&head,Tail&... tail){std::cin>>head;scan(tail...);}
#define LL(...) ll __VA_ARGS__;scan(__VA_ARGS__)
#define STR(...) string __VA_ARGS__;scan(__VA_ARGS__)
//vectorのcin
template<typename T>
std::istream &operator>>(std::istream&is,std::vector<T>&v){for(T &in:v){is>>in;}return is;}
//vectorのcout
template<typename T>
std::ostream &operator<<(std::ostream&os,const std::vector<T>&v){for(auto it=std::begin(v);it!=std::end(v);){os<<*it<<((++it)!=std::end(v)?" ":"");}return os;}
//dequeのcin
template<typename T>
std::istream &operator>>(std::istream&is,std::deque<T>&v){for(T &in:v){is>>in;}return is;}
//dequeのcout
template<typename T>
std::ostream &operator<<(std::ostream&os,const std::deque<T>&v){for(auto it=std::begin(v);it!=std::end(v);){os<<*it<<((++it)!=std::end(v)?" ":"");}return os;}
//pairのcin,cout
template<typename T,typename U>
std::ostream &operator<<(std::ostream&os,const std::pair<T,U>&p){os<<p.first<<" "<<p.second;return os;}
template<typename T,typename U>
std::istream &operator>>(std::istream&is,std::pair<T,U>&p){is>>p.first>>p.second;return is;}
//x,y,x,yを渡すとldで距離を返す
long double my_distance(long double xi,long double yi,long double xj,long double yj){return sqrtl(abs((xi-xj)*(xi-xj))+abs((yi-yj)*(yi-yj)));}
//可変長引数のprint関数
#pragma GCC diagnostic ignored "-Wunused-value"
void print(){cout << '\n';}
template<class T, class... Ts>
void print(const T& a, const Ts&... b){cout << a;(std::cout << ... << (cout << ' ', b));cout << '\n';}
#pragma GCC diagnostic warning "-Wunused-value"
//可変長引数のmin
template<class... T>
constexpr auto min(T... a){return min(initializer_list<common_type_t<T...>>{a...});}
//可変長引数のmax
template<class... T>
constexpr auto max(T... a){return max(initializer_list<common_type_t<T...>>{a...});}
template<typename T,typename U>inline bool chmax(T&a,U b){if(a<b){a=b;return 1;}return 0;}
template<typename T,typename U>inline bool chmin(T&a,U b){if(a>b){a=b;return 1;}return 0;}
template<typename T> inline T sum(vector<T>&a){T ret{};for(auto&i:a)ret+=i;return ret;}
template<typename T> inline T min(vector<T>&a){T ret=a[0];for(auto&i:a)chmin(ret,i);return ret;}
template<typename T> inline T max(vector<T>&a){T ret=a[0];for(auto&i:a)chmax(ret,i);return ret;}
template<typename T> inline int len(vector<T>&a){return a.size();}
inline int len(string&a){return a.size();}
// n次元配列の初期化。第２引数の型のサイズごとに初期化していく。
template<typename A, size_t N, typename T>
void Fill(A (&array)[N], const T &val){std::fill( (T*)array, (T*)(array+N), val );}
//こめんとを付け外ししてMODを切り替える
//ll MOD = INF;
// ll MOD = 1000000007;
ll MOD = 998244353;

//ax+by = 1 であるようなx,yを返す
// pair<long long, long long> extgcd(long long a, long long b) {
//   if (b == 0) return make_pair(1, 0);
//   long long x, y;
//   tie(y, x) = extgcd(b, a % b);
//   y -= a / b * x;
//   return make_pair(x, y);
// }

struct Rande {mt19937 mt;Rande(): mt(chrono::steady_clock::now().time_since_epoch().count()){}int operator()(int a, int b) {uniform_int_distribution< int > dist(a, b - 1);return dist(mt);}int operator()(int b){return (*this)(0, b);}};
//from:https://kenkoooo.hatenablog.com/entry/2016/11/30/163533 int128
std::ostream &operator<<(std::ostream &dest, __int128_t value) {std::ostream::sentry s(dest);if (s){__uint128_t tmp = value < 0 ? -value : value;char buffer[128];char *d = std::end(buffer);do{--d;*d = "0123456789"[tmp % 10];tmp /= 10;} while (tmp != 0);if (value < 0) {--d;*d = '-';}int len = std::end(buffer) - d;if (dest.rdbuf()->sputn(d, len) != len) {dest.setstate(std::ios_base::badbit);}}return dest;}
__int128 parsetoint128(string &s) {__int128 ret = 0;for (int i = 0; i < (int)s.length(); i++)if ('0' <= s[i] && s[i] <= '9')ret=10*ret+(__int128_t)(s[i]-'0');return ret;}

ll divide(ll a, ll b){if(b < 0) a *= -1, b *= -1;if(a >= 0) return a/b;else return -(((-a)+(b-1))/b);}
//回文判定 
bool iskaibun(string s){ll k = s.size();rep(i,0,k/2){if(s[i]!=s[k-1-i]){return false;}}return true;}

//二部グラフ判定 重みなしグラフを引数に取り、boolを返す
bool isbipartite_graph(vector<vector<ll>>&g){ll v = g.size();vector<ll>col(v,-1);vector<bool>used(v,false);bool ret = true;rep(i,v){if(used[i])continue;col[i]=0;[DFS([&](auto&&f,ll pos,ll pr)->void{if(used[pos])return;used[pos]=true;for(auto to:g[pos]){if(to==pr)continue;if(used[to]&&col[pos]==col[to]){ret = false;return;}if(used[to])continue;col[to]=col[pos]^1;f(f,to,pos);}}),&i]{DFS(DFS,i,-1);}();}return ret;}
//a~bの和 a<b
ll ran(ll a,ll b){return ((a+b)*(b-a+1))/2;}
//座圧する
ll zaatu(vector<ll>&A){map<ll,ll>m;for(auto&&x:A)m[x]=0;ll ret = 0;for(auto&&[key,val]:m)val=ret++;for(auto&&x:A)x=m[x];return ret;}
//約数列挙　引数に取った整数の約数のvectorを返す
vector<ll>enumdiv(ll n){vector<ll>s;for(ll i = 1;i*i<=n;i++){if(n%i==0){s.push_back(i);if(i*i!=n)s.push_back(n/i);}}return s;}
//トポロジカルソート グラフ、入次数カウント、頂点数を引数で渡すと、トポロジカルソートされた頂点列を返す
vector<ll> topo_sort(vector<vector<ll>>&G,vector<ll>&nyu_cnt,ll v){vector<ll>ret;priority_queue<ll,vector<ll>,greater<ll>>pq;rep(i,0,v){if(nyu_cnt[i]==0)pq.push(i);}while(!pq.empty()){ll pos = pq.top();pq.pop();for(ll i:G[pos]){nyu_cnt[i]--;if(nyu_cnt[i]==0)pq.push(i);}ret.push_back(pos);}return ret;}
//素因数分解 pair<素数、指数>のvectorを返す
vector<pair<ll, ll>> soinsu_bunkai(ll x){vector<pair<ll, ll>> ret;ret.reserve(1<<8);ll i = 2;for(i = 2;i<4;i++)if(x%i== 0){ll cnt{};while (x % i == 0){x /= i;cnt++;}ret.push_back({i, cnt});}for(i = 1;i*i<=x;i+=2){if(i>1)if(x%i==0){ll cnt{};while (x % i == 0){x /= i;cnt++;}ret.push_back({i, cnt});}i += 4;if(x%i==0){ll cnt{};while (x % i == 0){x /= i;cnt++;}ret.push_back({i, cnt});}}if (x != 1)ret.push_back({x, 1});return ret;}
//二項係数MOD MODは上の方で設定、MAXまでのnCrをCOM(n,r)でとれる
const int MAX = 777778;
ll fac[MAX], finv[MAX], invv[MAX];bool COMINIT=false;
void COMinit(){if(COMINIT)return;COMINIT=true;fac[0]=fac[1]=finv[0]=finv[1]=invv[1]=1;for(int i=2;i<MAX;i++){fac[i]=fac[i-1]*i%MOD;invv[i]=MOD-invv[MOD%i]*(MOD/i)%MOD;finv[i]=finv[i-1]*invv[i]%MOD;}}
ll COM(int n,int k){if(n<k)return 0;if(n<0||k<0)return 0;if(k==0)return 1;return fac[n]*(finv[k]*finv[n-k]%MOD)%MOD;}
ll nPr(int n,int k){if(n<k)return 0;if(n<0||k<0)return 0;if(k==0)return 1;return fac[n]*(finv[n-k]);}
//エラトステネスの篩　isprimeには素数かどうかが入っている
vector<bool> isprime;vector<int> Era(int n) {isprime.resize(n, true);vector<int> res;isprime[0] = false; isprime[1] = false;for (int i = 2; i < n; ++i) isprime[i] = true;for (int i = 2; i < n; ++i){if (isprime[i]) {res.push_back(i);for (int j = i*2; j < n; j += i) isprime[j] = false;}}return res;}
//Union-Find from https://zenn.dev/reputeless/books/standard-cpp-for-competitive-programming/viewer/union-find
class UnionFind{public:UnionFind()=default;explicit UnionFind(size_t n):m_parentsOrSize(n, -1){}int find(int i){if(m_parentsOrSize[i]<0){return i;}return(m_parentsOrSize[i]=find(m_parentsOrSize[i]));}void merge(int a,int b){a=find(a);b=find(b);if(a!=b){if(-m_parentsOrSize[a]<-m_parentsOrSize[b]){std::swap(a,b);}m_parentsOrSize[a]+=m_parentsOrSize[b];m_parentsOrSize[b]=a;}}bool connected(int a,int b){return (find(a)==find(b));}int size(int i){return -m_parentsOrSize[find(i)];}private:std::vector<int>m_parentsOrSize;};
template <class T> using pqg = priority_queue<T, vector<T>, greater<T>>;
template <class F> ll bin_search(ll ok,ll ng,const F&f){while(abs(ok-ng)>1){long long mid=(ok+ng)>>1;(f(mid)?ok:ng)=mid;}return ok;}
//グリッドの8近傍 4まで回せば4近傍
ll dx[8] = {0,1,0,-1,-1,-1,1,1},dy[8]={1,0,-1,0,-1,1,-1,1};
constexpr ld CPS = CLOCKS_PER_SEC;

bool solve();
void _main(){
[]{[]{[]{[]{[]{}();}();}();}();}();
	int testcase = 1;
	// cin >> testcase,cerr<<"multitestcase"<<endl;
	for(;testcase--;){
		if(solve()){
			// O("Possible");
		}
		else{
			// O("Impossible");
		}
	}
	cout<<flush;
[]{[]{[]{[]{[]{}();}();}();}();}();
}
#include<atcoder/all>
using namespace atcoder;
// using mint = modint;
using mint = modint998244353;
using mint1 = modint1000000007;


bool solve(){
	
	return false;
}

　詳細な解説を書きたいのですが、時間をとれておらず...いつか絶対作ります。

プログラミングの経験年数など

入水記事に書きました。

習得したアルゴリズム

この方の記事を参考に書きます。

• 〇→まあ使える
• ◎→得意！
• △→微妙、調べれば使える
• ×→使えない
• ？→聞いたことがない、聞いたことしかない

グラフ

アルゴリズム	習得度
ダイクストラ法	◎
拡張ダイクストラ	◎
ワーシャルフロイド法	◎
ベルマンフォード法	◎
オイラーツアー	○
トポロジカルソート	◎
プリム法	△
クラスカル法	◎
強連結成分分解	◎
HL分解	△
木の直径	◎
LCA	◎
最大流/最小カット	○

探索

アルゴリズム	習得度
幅優先探索(BFS)	◎
深さ優先探索(DFS)	◎
bit全探索	◎
半分全列挙	◎
順列全探索	◎
二分探索	◎
三分探索	○
答えで二分探索	◎
しゃく取り法	○
Mo's Algorithm	○

DP

アルゴリズム	習得度
1次元DP	◎
2次元DP	◎
最長共通部分列	○
最長増加部分列	○
区間DP	◎
期待値DP	○
確率DP	◎
bitDP	◎
桁DP	○
耳DP	○

数学/幾何

アルゴリズム	習得度
GCD/LCM	◎
累積和	◎
いもす法	◎
二次元累積和	◎
素因数分解	◎
約数列挙	◎
高速素数判定	◎
高速素因数分解	○
素数列挙	◎
繰り返し二乗法	○
回転行列	○
逆元/MOD上の割り算	○
拡張ユークリッドの互除法	△
行列累乗	◎
FPS	○
CRT(中国剰余定理)	○

データ構造

アルゴリズム	習得度
Union-Find	◎
map	◎
set	◎
multiset	◎
BIT	◎
SegmentTree	◎
LazySegmentTree	〇
2DSegmentTree	○
Sparse Table	○
Disjoint Table	○
WaveletMatrix	○

その他

アルゴリズム	習得度
座標圧縮	◎
RLE(ランレングス圧縮)	◎
ローリングハッシュ	×
彩色数を求めるアルゴリズム	△
包除原理	○

青から黄色になるまでにやったこと

強くなりたいなら、効率をある程度度外視するのも大事だと思います。ここでは最近の1年間でやったことを振り返ります。入青記事にあった内容は省略します。

精進

当たり前ですが、精進をしました。ABC/ARCの問題を主に解いていましたが、AGCの問題も解いていました。有志コンテストの問題はあまり解いていません。ただ、典型90やEDPCは解いています。

自分は一日にまとめてやるよりはコツコツと継続する方が得意だったので、毎日適当な黄Diffを見繕って解く、というような精進をしていました。時間が取れるときには橙Diffを解きに行ったりもしていましたが、本番ではあまり活かせていません。

有志コンの運営

主催ではないですが、緑以下コンテストと水以下コンテストの運営に参加していました。大きな貢献はできませんでしたが、自分にとって良い経験になったと思います。そもそもTwitterでしか関わらない競プロerと実際に出会うのはすごく楽しいです！

「朝練」「昼練」

自分はTCAという部活の責任者をしているのですが、その部活の朝練という形で毎朝バーチャルコンテストを立てていました。最初は手動で立てていましたが、部員が途中からbotで自動化してくれました。

主に茶～緑Diffの早解きと、青Diffの継続的な考察のために行っていました。ABCの序盤の早解きがかなり強くなりました。

noteに日記を書く

これは最近は行っていないのですが、毎日解いた問題やそのポイントなどをまとめてnoteに投稿していました。

部活でABCの解説

高校2年生になり、部活にも後輩が入ってきました。1年生には競プロに熱心な人も多く、部内の競プロer濃度が高くなっていたので、毎週月曜日に前回のABCについての解説を行うようになりました。

解説といってもちゃんと解説するというよりは問題の振り返りを行うという感じで感想戦に近いものではありますが、自分にとっても部員にとっても有益な時間になっていると思います。

ABCの解説を書く

これは黄色になってからやったことでもありますが、解説記事はもともとScrapBoxで書いていました（入青記事参照）。黄色になってからはABCの解説を書く権利が得られたので、よりちゃんとした解説をいくつか投稿しています。

解説記事、といえるほどちゃんとしたものではなくても、他の人に見せられるほどのクオリティがなくとも、自分が解いた問題の解法やポイントを言語化してまとめておくのはかなり大事なことだと思います。

海外コンに参加

CodeForces/CodeChefにもたまに参加していました。が、時間帯的にほとんど参加できませんでした。ABCばかり解いていると解ける問題に偏りができてしまうので、できるだけ参加したり問題を解いたりしておきたいところです。ただ、黄色を目指すだけならABC/ARCのみを解いていても十分だと思います。

ちなみに、黄色を目指す上でもARCは参加した方がいいと思います。ABCの安定を完璧にするよりも、ARCである程度戦えるようにする方が楽だからです。ただ、リスクは高めではあると思います。

新規アルゴリズムの勉強

先ほどの「習得したアルゴリズム」には載せていませんでしたが、定期的に新しいアルゴリズム/データ構造を学んでいました。

ただ問題を解くよりも新しいことを学んだ方が楽しいので、定期的に行っています。

ここで学んでいた中でTrie木を知り、そのおかげで本番で解くことができた問題もあります。

これからの展望

まずは再入黄を目指したいです。ただ、黄色を目指していては橙にはなれないと思うので、ARCや海外コンの問題も解いていきたいです。

JOIもあります。二次予選を突破したので次は本戦です！去年は本番で大コケしてしまったこともあり春合宿に行くことができず、悔しかったです。今年は春合宿に行きたいです！

また、部長として部員に競プロを教えるのも頑張りたいです。僕は人に教えるのは大好きだし、教えることで学びもあると思うからです。

加えて、自分が学んだことを言語化して残しておくことも大事にしたいです。上に書いたことと被りますが、言語化するのは得意だと思っているので、初学者が少しでも楽になるような手助けができたらいいなと思っています。

おわりに

最後まで読んでくださりありがとうございました！引き続き精進頑張ろうと思います。次回は入橙記事で会いましょう！