【Atcoder】高校1年生でAtcoder青色になりました

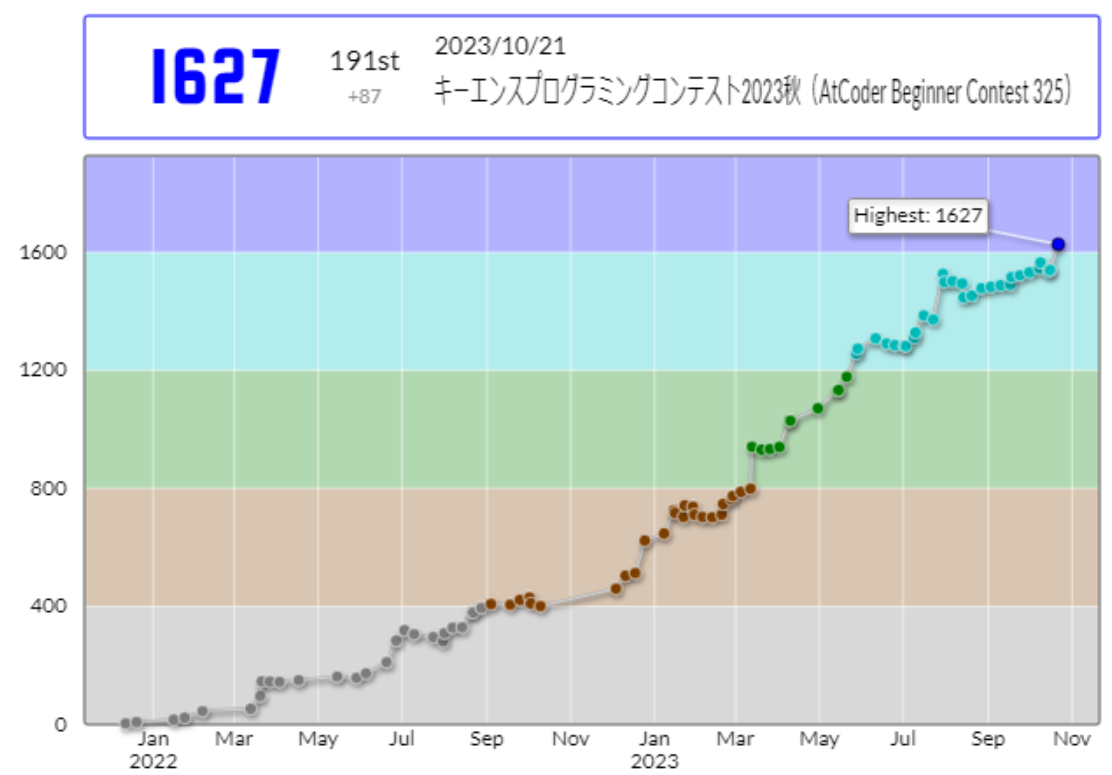
こんにちは、Blueberryです。先日行われたABC325で、念願の入青を果たすことができました！！
とてもうれしいので記事を書きます。

入水記事→【Atcoder】高校1年生でAtcoder水色になりました
入青動画→【ゆっくり実況】AtCoder Beginner Contest 325

AtCoderについて知らない方、各色のレベル感を知りたい方はこちらを参照してください。（AtCoder社長による色別評価です）AtCoder（競技プログラミング）の色・ランクと実力評価、問題例

※この記事は非常に長いです。お時間のあるときにどうぞ。

はじめに

レート遷移です。

5/28に入水し、10/21に入青しているので、約5か月で入青したことになります。入緑から入水までが早かったので、それに比べるとかなり時間がかかったなと思います。水色で停滞する人をよく見かけるので、一般的には割と早い方かもしれません。

どうやったら青色になれるの？

　色変記事といえばこれなので書きます。

　まず競プロを始めたばかりの方へのアドバイスです。入水記事にも書いたことですが、初心者の方はまずはわからないところはどんどん調べてプログラミングに慣れていくことが大事だと思います！プログラムが書けるようになってきたらひたすら問題を解きましょう！最初はABC-Aを最新順に解いていき、慣れてきたらB問題に挑戦したり、茶色の問題に挑戦したりするといいと思います。また、まず全探索をマスターすることはとても重要なので全探索についていろいろ調べながら競プロに慣れていくといいと思います。

　次にある程度競プロに慣れている方へ。ひたすら問題を解きましょう！！とにかくたくさんの問題を解いてさまざまな典型を習得することが上達への一番の近道だと思います。レートが停滞してしまうなど、本当に自分の努力の方向性は正しかったのか？と不安になることもあると思います。でもその努力はいつかきっと報われます。自分を信じて頑張りましょう！

　「低難度を埋めるのは効果が薄い」という意見もありますが、僕はやる前から効果が薄いと決めつけるのではなく、強くなるためにできることは何でもするべきだと思っています。（もちろん、効率的な精進をするべきという意見もわかります。あくまで僕の意見です。）

　また、こうやって色々と自分の意見を語っておいてなのですが、情報収集に重要なのは一つの情報源からの情報を過度に信じすぎないことです。いろいろな色変記事などを読んで、自分なりの精進の方法を見つけると良いでしょう。毎日解くのが得意だという人もいれば、一気にまとめてたくさん解くのが得意という人もいるでしょう。がんばり方はひとそれぞれです。

　もうちょっと詳しい話は下の方でまたします。

テンプレート

　僕はC++をメインで使っているので、使っているテンプレートを紹介しようと思います。C++以外の方は読み飛ばしてもらって大丈夫です。まずは全体像を貼ります。

using namespace std;
#include<bits/stdc++.h>
void _main();int main(){cin.tie(0);ios::sync_with_stdio(false);cout<<fixed<<setprecision(30);_main();return 0;}
#pragma GCC target("avx2")
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")
typedef long long ll;typedef long double ld;
#define rep1(a)          for(int i = 0; i < (a); i++)
#define rep2(i, a)       for(int i = 0; i < (a); i++)
#define rep3(i, a, b)    for(int i = (a); i < (b); i++)
#define rep4(i, a, b, c) for(int i = (a); i < (b); i += (c))
#define overload4(a, b, c, d, e, ...) e
#define rep(...) overload4(__VA_ARGS__, rep4, rep3, rep2, rep1)(__VA_ARGS__)
#define ALL(x) std::begin(x),std::end(x)
#define rALL(x) std::rbegin(x),std::rend(x)
#define INF ((1LL<<62)-(1LL<<31))
#define bit(x,i) (((x)>>(i))&1)
#define fi first
#define se second
#define pb push_back
#define Endl endl
#define spa " "
#define YesNo(x) cout<<(x?"Yes":"No")<<endl;

#include <atcoder/all>
using namespace atcoder;

//コンパイル時の引数にBLUEBERRYを渡すとdeb関数が使える
#ifdef BLUEBERRY
#define deb print
#else
#define deb 
#endif
//！？！？
#define O print
//可変長引数で入力を受け取りつつ変数を宣言
inline void scan(){}
template<class Head,class... Tail>
inline void scan(Head&head,Tail&... tail){std::cin>>head;scan(tail...);}
#define LL(...) ll __VA_ARGS__;scan(__VA_ARGS__)
#define STR(...) string __VA_ARGS__;scan(__VA_ARGS__)
//vectorのcin
template<typename T>
std::istream &operator>>(std::istream&is,std::vector<T>&v){for(T &in:v){is>>in;}return is;}
//vectorのcout
template<typename T>
std::ostream &operator<<(std::ostream&os,const std::vector<T>&v){for(auto it=std::begin(v);it!=std::end(v);){os<<*it<<((++it)!=std::end(v)?" ":"");}return os;}
//x,y,x,yを渡すとldで距離を返す
long double my_distance(long double xi,long double yi,long double xj,long double yj){return sqrt(abs((xi-xj)*(xi-xj))+abs((yi-yj)*(yi-yj)));}
//可変長引数のprint関数
void print(){cout << '\n';}
template<class T, class... Ts>
void print(const T& a, const Ts&... b){cout << a;(cout << ... << (cout << ' ', b));cout << '\n';}
//可変長引数のmin
template<class... T>
constexpr auto min(T... a){return min(initializer_list<common_type_t<T...>>{a...});}
//可変長引数のmax
template<class... T>
constexpr auto max(T... a){return max(initializer_list<common_type_t<T...>>{a...});}
template<typename T,typename U>inline bool chmax(T&a,U b){if(a<b){a=b;return 1;}return 0;}
template<typename T,typename U>inline bool chmin(T&a,U b){if(a>b){a=b;return 1;}return 0;}
//Union-Find from https://zenn.dev/reputeless/books/standard-cpp-for-competitive-programming/vi((b%2==0?b-1:b)+2-(a%2==0?a+1:a))/2er/union-find
class UnionFind{public:UnionFind()=default;explicit UnionFind(size_t n):m_parentsOrSize(n, -1){}int find(int i){if(m_parentsOrSize[i]<0){return i;}return(m_parentsOrSize[i]=find(m_parentsOrSize[i]));}void merge(int a,int b){a=find(a);b=find(b);if(a!=b){if(-m_parentsOrSize[a]<-m_parentsOrSize[b]){std::swap(a,b);}m_parentsOrSize[a]+=m_parentsOrSize[b];m_parentsOrSize[b]=a;}}bool connected(int a,int b){return (find(a)==find(b));}int size(int i){return -m_parentsOrSize[find(i)];}private:std::vector<int>m_parentsOrSize;};

//こめんとを付け外ししてMODを切り替える
//ll MOD = INF;
ll MOD = 1000000007;
//ll MOD = 998244353;

//回文判定 
bool iskaibun(string s){ll k = s.size();rep(i,0,k/2){if(s[i]!=s[k-1-i]){return false;}}return true;}

//二部グラフ判定 重みなしグラフを引数に取り、boolを返す
bool isbipartite_graph(vector<vector<ll>>&g){ll v = g.size();vector<ll>col(v,-1);vector<bool>used(v,false);bool ret = true;rep(i,v){if(used[i])continue;col[i]=0;[DFS([&](auto&&f,ll pos,ll pr)->void{if(used[pos])return;used[pos]=true;for(auto to:g[pos]){if(to==pr)continue;if(used[to]&&col[pos]==col[to]){ret = false;return;}if(used[to])continue;col[to]=col[pos]^1;f(f,to,pos);}}),&i]{DFS(DFS,i,-1);}();}return ret;}
//a~bの和 a<b
ll ran(ll a,ll b){return ((a+b)*(b-a+1))/2;}
//Pythonにあるreplaceみたいなもの 森久保さん作
string replace(const string&moto,const string &from,const string&too){int from_len = from.size();string tmp=from+moto;int tmp_len=tmp.size();vector<int>za=atcoder::z_algorithm(tmp);string ret="";for (int i=from_len;i<tmp_len;){if(za[i]>=from_len){ret+=too;i += from_len;}else{ret += tmp[i];i++;}}return ret;}
//座圧する
ll zaatu(vector<ll>&A){map<ll,ll>m;for(auto&&x:A)m[x]=0;ll ret = 0;for(auto&&[key,val]:m)val=ret++;for(auto&&x:A)x=m[x];return ret;}
//約数列挙　引数に取った整数の約数のvectorを返す
vector<ll>enumdiv(ll n){vector<ll>s;for(ll i = 1;i*i<=n;i++){if(n%i==0){s.push_back(i);if(i*i!=n)s.push_back(n/i);}}return s;}
//トポロジカルソート グラフ、入次数カウント、頂点数を引数で渡すと、トポロジカルソートされた頂点列を返す
vector<ll> topo_sort(vector<vector<ll>>&G,vector<ll>&nyu_cnt,ll v){vector<ll>ret;priority_queue<ll,vector<ll>,greater<ll>>pq;rep(i,0,v){if(nyu_cnt[i]==0)pq.push(i);}while(!pq.empty()){ll pos = pq.top();pq.pop();for(ll i:G[pos]){nyu_cnt[i]--;if(nyu_cnt[i]==0)pq.push(i);}ret.push_back(pos);}return ret;}
//素因数分解 pair<素数、指数>のvectorを返す
vector<pair<ll,ll>> soinsu_bunkai(ll x){vector<pair<ll,ll>>ret;rep(i,2,sqrt(x)+1){if(x%i==0){ll cnt{};while(x%i==0){x/=i;cnt++;}ret.push_back({i,cnt});}}if(x!=1)ret.push_back({x,1});return ret;}
//二項係数MOD MODは上の方で設定、MAXまでのnCrをCOM(n,r)でとれる
const int MAX = 5000000;
ll fac[MAX], finv[MAX], invv[MAX];
void COMinit(){fac[0]=fac[1]=finv[0]=finv[1]=invv[1]=1;for(int i=2;i<MAX;i++){fac[i]=fac[i-1]*i%MOD;invv[i]=MOD-invv[MOD%i]*(MOD/i)%MOD;finv[i]=finv[i-1]*invv[i]%MOD;}}
ll COM(int n,int k){if(n<k)return 0;if(n<0||k<0)return 0;if(k==0)return 1;return fac[n]*(finv[k]*finv[n-k]%MOD)%MOD;}
ll nPr(int n,int k){if(n<k)return 0;if(n<0||k<0)return 0;if(k==0)return 1;return fac[n]*(finv[n-k]);}
//エラトステネスの篩　isprimeには素数かどうかが入っている
vector<bool> isprime;vector<int> Era(int n) {isprime.resize(n, true);vector<int> res;isprime[0] = false; isprime[1] = false;for (int i = 2; i < n; ++i) isprime[i] = true;for (int i = 2; i < n; ++i){if (isprime[i]) {res.push_back(i);for (int j = i*2; j < n; j += i) isprime[j] = false;}}return res;}


using mint = modint998244353;

void solve();
void _main(){
    int testcase = 1;
    //cin >> testcase;
    for(;testcase--;){
        solve();
    }
}
void solve(){
    
}

　詳細な解説を書くべきかTwitterで投票を取ったところ、解説を書いてほしいという意見が多かったのですが、12/1に間に合いそうになかったので別の記事で書きます！

プログラミングの経験年数など

入水記事に書きました。

習得したアルゴリズム

この方の記事を参考に書きます。

• 〇→まあ使える
• ◎→得意！
• △→微妙、調べれば使える
• ×→使えない
• ？→聞いたことがない、聞いたことしかない

グラフ

アルゴリズム	習得度
ダイクストラ法	○
ワーシャルフロイド法	○
ベルマンフォード法	○
オイラーツアー	△
トポロジカルソート	○
プリム法	△
クラスカル法	◎
強連結成分分解	○
HL分解	△
木の直径	○
LCA	○
最大流/最小カット	△

探索

アルゴリズム	習得度
幅優先探索(BFS)	◎
深さ優先探索(DFS)	◎
bit全探索	◎
半分全列挙	◎
順列全探索	◎
二分探索	◎
三分探索	○
答えで二分探索	△
しゃく取り法	○
Mo's Algorithm	○

DP

アルゴリズム	習得度
1次元DP	◎
2次元DP	○
最長共通部分列	○
最長増加部分列	○
区間DP	○
期待値DP	○
確率DP	◎
bitDP	○
桁DP	○
竹DP	？
耳DP	？

数学/幾何

アルゴリズム	習得度
GCD/LCM	◎
累積和	○
いもす法	△
二次元累積和	○
素因数分解	○
約数列挙	○
高速素数判定	◎
素数列挙	◎
繰り返し二乗法	○
回転行列	？
逆元/MOD上の割り算	○
拡張ユークリッドの互除法	×
行列累乗	○
FPS	○
CRT(中国剰余定理)	○

データ構造

アルゴリズム	習得度
Union-Find	◎
map	◎
set	◎
multiset	○
BIT	△
SegmentTree	○
LazySegmentTree	〇
2DSegmentTree	○
Sparse Table	×
WaveletMatrix	×

その他

アルゴリズム	習得度
座標圧縮	◎
RLE(ランレングス圧縮)	◎
ローリングハッシュ	×
彩色数を求めるアルゴリズム	△
包除原理	○

その他、TLで見かけた高度そうなアルゴリズムはまだストックしてあります。いつか習得したい...！

水色から青になるまでにやったこと

　どうやったら青色になれるの？では、AtCoderを始めて青色に至るまでの方法について書きました。先程も書いた通り、とにかく数をこなすことが一番強いのですが、ここではもう少し具体的に、水色から青になるまでに何をしたかを書いていこうと思います。（一部、青になってからやったことも含まれていますが、青を目指すうえでも問題ないと思います）

Streakを繋ぐ

　まず毎日最低でも1問は解きます。継続は力ともいわれるように、毎日の積み重ねは必ず活きてきます。ここで重要なのは、簡単すぎる問題に逃げないことです。（ただし、日常的に行うのでなければ、例えば1日中予定が詰まっていて競プロの時間を十分に取れないというときに低難度でStreakをつなぐのはアリだと僕は思っています。Streakをモチベーションにして精進する場合、切れたときのモチベーション低下が響くからです。）
　簡単すぎる問題に逃げないためにはいくつか方法があります。
　1つ目に、簡単すぎる問題を埋めてしまうということです。Streakは新規ACでしか繋ぐことができないため、簡単すぎる問題でStreakを繋ぐことが不可能になります。
　2つ目は次の項目ですね。

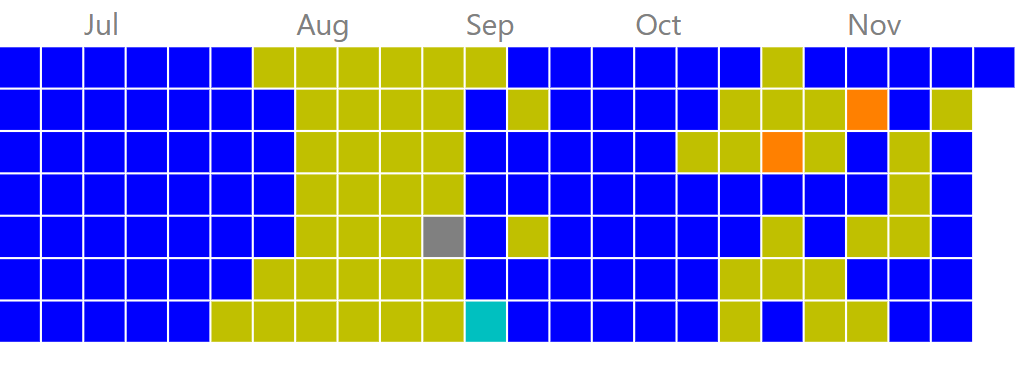
青Streak/黄Streak

です。

　格上の問題に挑む習慣がつき、解けなかった問題が解けるようになったり、新たな典型を身につけることができますし、Heatmapがこのようにきれいな色になるのでモチベーションも上がります。

EDPC

EDPCの問題を解き、さまざまなDPの形を知りました。

JOI

　情報オリンピックも近いので情報オリンピックの過去問を解いています。実装力が試される問題が多い印象です。

バーチャルコンテスト

　新しい問題を解くだけでなく、以前に解いた問題をもう一度解くことも重要です。しかしなかなかすでにACした問題を解こうという気持ちにはなれません。そこでバーチャルコンテストに出ることで、早解き練習なども兼ねて以前解いた問題を復習したり、まだ解いていない問題に出会ったりすることができます。
早解き練習はなかなかできないと思うので、バーチャルコンテストはその意味でも良いと思います。

Scrapbox

　Scrapoxに、学んだアルゴリズムのメモやライブラリの使用方法のメモ、解いた問題の個人的な振り返りを書いています。
　ライブラリの使い方は自分で使ってみて自分で書いた方がわかりやすいので、たまにコンテスト中にも確認しに来ることがあります。
　問題の振り返りは、書くことでまずその問題の解法をきちんと理解できているか確認することができます。また、その問題に含まれている典型要素を認識することができ、次に同じような問題に出会ったときに活かすことができます。

環境構築

　順番がおかしいようにも見えますが、僕は環境構築に大きな苦手意識がありほとんどやってきませんでした。それでも最近は少し環境構築を頑張って、便利になったのでこれも別で記事か動画を作ろうと思っています。

Q&A

ここからはTwitterでマシュマロを使って募集して来た質問に答えていきます。

1.

　学業：競プロは0:1ですね...（もちろん課題はやりますが、普段の学習時間はほぼ0です...）
精進から学業への還元率というのは、競プロが学業で役に立つ時を指しているのでしょうか？それなら数学ではたまに競プロが役に立つときがありますね。%はわからないです...

2.

　ありがとうございます！解く問題はAtCoder ProblemsのRecommendationをしばらく解いていましたが、最近はABCの問題がほとんどRecommendationに出てこなくなってしまった（Recommendationに出てくるABCの問題をほとんど解いてしまった）ので、ABCのE~Fで青～黄で未ACの問題を解いています。

　モチベーションについては下で詳しく書きます。（先に言っておきますがとても長いです、暇な方以外読まなくて大丈夫です）

3.

　区間DP、Monge、マトロイド、FFT/NTT、Slope trick、その他文字列系（Z-algorithm,Suffix-Array,LCP Arrayローリングハッシュ）
　あとはFPSとフローをちゃんと解けるようにしたいです。
　他に学ぶべきものがあればコメント等で頂けると助かります...！

4.

　いま目指しているのは黄色です。まだ、「赤を目指す」と言える位置にいないと思っています。まずは目の前の目標に向かって頑張ろうと思っています。

5.

　3~5時間ぐらいですかね。動画の長さにもよりますが、細かいタイミング調整が一番時間かかります。あとはやる気さえ出れば一気に進むのですが、やる気が出ないと完成させられずにしばらく放置してしまいます...
話がそれますが、実況動画だけでなく解説動画なんかも作ってみたいですね～
Youtubeチャンネルはこちら

6.

毎朝5時に起きて家の近くを走っています。

7.

鶏肉料理全般ですね～。お菓子だとチョコが好きです。
とはいえ好みはあんまりないですね、お菓子も普段はあまり食べないです。コンテスト中の糖分補給用にチョコがあるとうれしいなというぐらいです。

8.

　普段は23時に寝て5時に起きています。睡眠時間は6時間なので足りないですね...ただリアルの知り合いやTwitterで見かける方々の中にはもっと睡眠時間が少ない人がたくさんいるので、一応睡眠時間は確保できている方だと思います。
　競プロ以外の時間を減らすことで、睡眠時間を減らさずに競プロの時間を増やすことができるので最近は意識的にこれをしています（ツイ廃を脱却したり、テレビゲームをほとんどやらなくなったりなど）

9.

　競プロ界隈でたびたび話題になる話ですね...よくPythonとC++が戦争をしているイメージがあります。質問が来たので僕の意見を述べておきます。
僕はC++が一番やりやすいと思っています。理由はいくつかあります。C++は実行時間が速い、Pythonは実行時間が遅いとよく言われますが、僕がPythonを使わない理由は、Pythonだと「競技プログラミングではない部分」に意識を割かなければならない気がしているからです。Pythonは入門しやすさとは裏腹に、きちんと理解していないと踏んでしまう罠が多いと思います。Pythonで競技プログラミングをするならPythonの知識がたくさん必要で、それならC++の方がまだ学習コストは低いと思います。
　まあ結局は好みで選べばいいと思います！JOIに出る場合はC++一択になってしまいますが、AtCoderなら様々な言語を使うことができますし。自分がやりやすい言語でやればいいと思います！ただ、まっさらな状態から始める場合はC++がおすすめです。AtCoder公式もC++の入門書を用意していますし、解説にもC++のコードが書かれていることが多いです。

モチベーションについて

僕の競プロのモチベーションについて話します。僕のレートグラフを見てわかるように、僕は競プロを始めた時期と精進を始めた時期は1年ほどずれています。精進グラフ（解いた問題の点数の合計の遷移をレートグラフに重ねてくれるUserScriptです）
を見るとわかりやすいです。

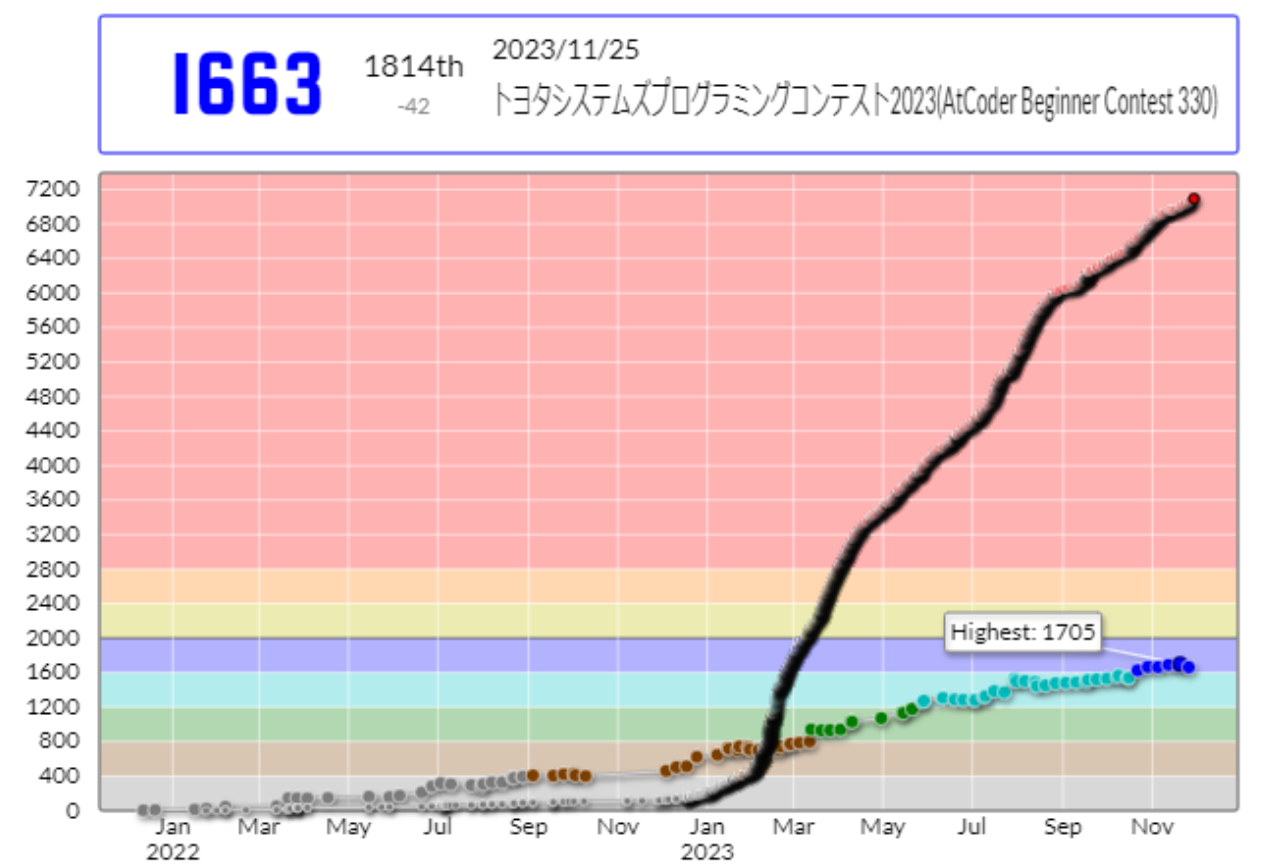
　僕は2022/12/20から今まで、競プロの問題を解かなかった日は1日もありません。（Streakは一回だけ切らしていますが、その日も問題自体は解いていました）

　ではこの12/20付近に何があったのかという話です。当時の僕は、今ほど競プロに力を注いではおらず、コンテストに毎週出ている程度でした。それでも茶色になっていたので、「僕、もしかしたら同年代の中でも結構つよいかもしれない！！」とか思っていました。

　ある日、ふとしたことがきっかけでAtCoderのレートのランキングを眺めていました。絞り込み機能があることに気づき、「せっかくだし同じ2007年生まれ、日本で絞り込んでみるか〜」と思い、絞り込みました。先程も話した通り、当時の僕にはそこそこ自信があったので、「まあ上の方に水色が2,3人いるぐらいかな〜」とか思っていました。

　実際のランキングを見て愕然としました。橙が、います。黄色がいます。青色がいます。水色が、緑が、たくさんいます。自分よりも格上の人が、同学年だけでこんなにもたくさんいます。上には上がいました。自分が大した事ないということを知って、少し落ち込みました。

　その少し後、ランキング上位にいた橙コーダーのAtCoder Problemsを覗きました。その方は3000問以上を解いていました。それを見て、「上位勢は地頭がいいだけでそこに辿り着いたのではなく、地頭がいいうえにすさまじい努力をしている」ことを知りました。とてもかっこいいな、と思いました。「自分もいつかこの人たちと肩を並べるような競プロerになりたい。そのためには、この人たちよりもたくさん努力しなければならない。」と思いました。これが僕の精進の原点です。

これからの展望

　まずは直近で情報オリンピック二次予選があります。実力的には問題なく通過できるとされているラインにいるとは思いますが、油断は禁物です。気を引き締めてかかろうと思います。長時間コンテストにあまり慣れていないので長時間の体調管理などを確認する意味でもしっかりと全力を出したいと思います。

　次に情報オリンピック本戦があります。春合宿に行きたいです。今からこのペースでがんばり続ければ不可能ではないと思っています。本戦までの残り約2か月で、少しでも春合宿へ行ける確率を高めたいと思います。

　そして、黄色コーダーになりたいです。黄色になるとABCがRatedで出れなくなったり、青から黄色は寒色から暖色だったりするなど、黄色には特別感もあります。また、僕の愛用しているアイコンのプーさんは黄色です。黄色コーダーに、なりたいです。

おわりに

最後まで読んでくださりありがとうございました！引き続き精進頑張ろうと思います。次回は入黄記事で会いましょう！