『Pythonで学ぶ強化学習 入門から実践まで』を読んでみた 第一章

#きっかけ
自分はとある事情で強化学習で迷路を解きたいと思いました。

その前に基礎を勉強しようとして買ったのがこの本『Pythonで学ぶ強化学習　入門から実践まで』—久保隆宏

しかし、かなり分かりやすい本なのに一度目はあんまり理解してない、、、

アウトプットした方がいいよていうふうに昔聞いたのを思い出し、この本の内容を自分なりに理解した内容を書きました。(引用多めです、、、)

一部間違いがあるかもしれませんが、ご指摘いただければありがたいです。

#強化学習とは
強化学習(Reinforcement Learning)、AlphaGoとかAlphaZeroとかが有名ですよね。

簡単な例として、
ブロック崩しのゲームで強化学習を訓練するパターンがあります。
Deepmindが出している動画があるのでぜひ見てみてください。
https://www.youtube.com/watch?v=TmPfTpjtdgg

1、最初は全然当たらなないけど、たまたまボードに当たったとき(ポイント)報酬を得る。
2、どうやったら(ポイント)報酬を得るのか試行錯誤していくうちに、ボードはに当たればよい→ブロックを崩せばいいんだと学習する。
3、どうやったら(ポイント)報酬が一番大きくなるか試行錯誤していくうちに、壁や天井に反射させた方が(ポイント)報酬は高いと学習する。
4、この試行錯誤を何千回と繰り返すうちに、人間を超えるブロック崩しの達人になる！

ざっくりだがお分りいただけただろうか？
報酬を求めて勝手に学習してくれるんだすげーくらいの感覚で大丈夫です。

###強化学習の特性

• 行動に対する報酬(＝正解)がある
  　　教師あり学習に少し似ている。

• 行動は「報酬の総和」の最大化につながる観点から評価される。

• つまり行動単体でなく、連続した行動が必要である。
• 1回ボールを跳ね返す報酬でなく、1ゲームの報酬ということ。

• 環境開始から終了までの期間を1エピソード(Episode)とする

• ブロック崩しなら1ゲームが1エピソード

• 強化学習の目的：1エピソードで得られる報酬の総和を最大化する

• 強化学習モデルが学ぶこと

1、行動の評価方法
2、（評価に基づく）行動の選び方＝戦略

##マルコフ性

強化学習では
与えられた環境が一定のルールに従っていることを想定する
そのルール（性質）をマルコフ性(Markov property)と呼ぶ
「遷移先の状態は直前の状態とそこでの行動のみに依存する。
報酬は、直前の状態と遷移先に依存する」

※簡単に言えば
遷移先の状態は直前の状態とそこでの行動のみに依存する→$T(s,a)$
報酬は、直前の状態と遷移先に依存する→$R(s,s')$
詳しくは下の文章を読むこと

※「遷移先」というのは「次の状態」と理解してよい

マルコフ性を持つ環境をマルコフ決定過程(Markov Decision Process：MDP)と呼ぶ
MDPの4つの構成要素
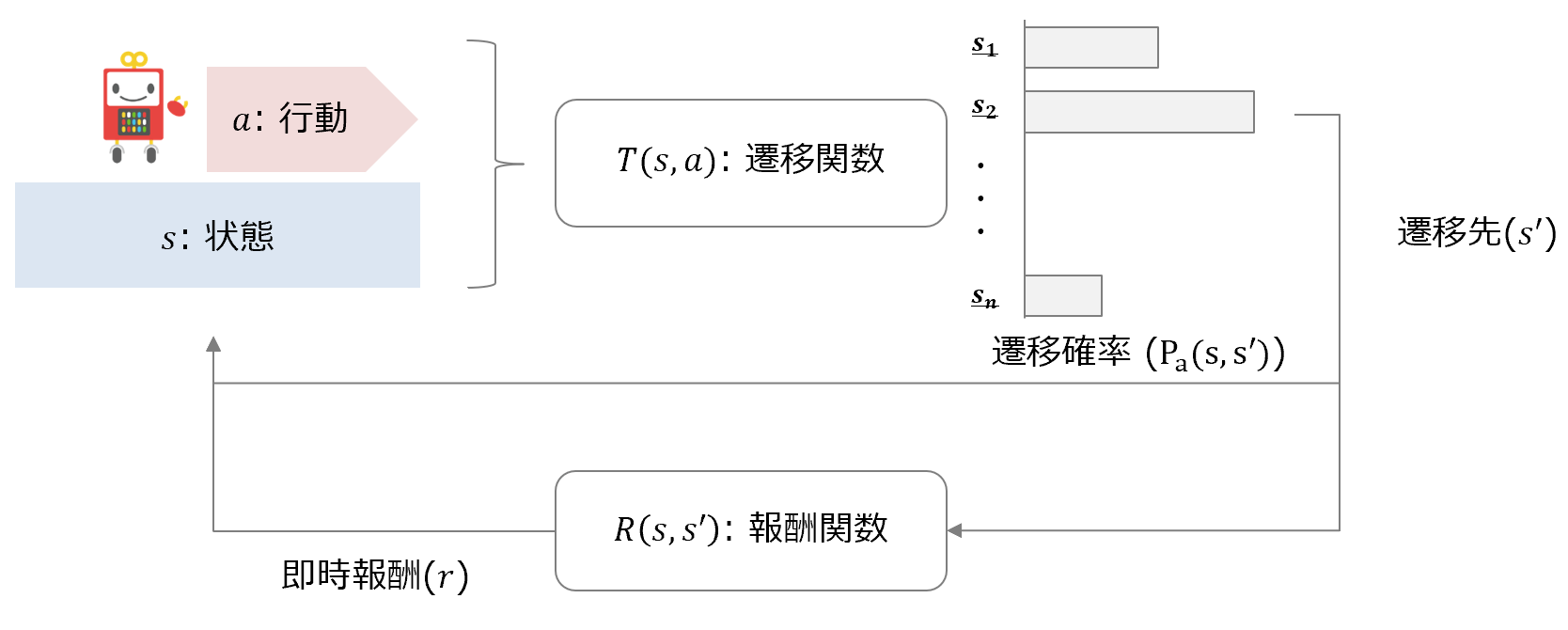
$s$：状態(State)
$a$：行動(Action)
$T$：状態遷移の確率(遷移関数/Transition function)
状態と行動を引数に、遷移先(次の状態)と遷移確率$P_{a}$を出力する関数。

※
入力：行動$a$,状態$s$
遷移関数：$T\left( s,a\right)$
出力：遷移先$s'$、遷移確率$P_{a}\left( s,s'\right)$

$R$：即時報酬(報酬関数/Reward function)
状態と遷移先を引数に、報酬を出力するような関数(行動を引数にとる場合も)

※
入力：状態$s$,遷移先(次の状態)$s'$
報酬関数：$R\left( s,s'\right)$
出力：即時報酬 $r$

$\pi$：戦略(Policy)状態を受け取り、行動を出力する関数
戦略に沿って動く主体エージェント(Agent)と呼ぶ。

※一部では$\pi$を方策と呼んでいますがここでは戦略と統一します。

• 戦略のパラメータを調整し、状態に応じ適切な行動を出力できるようにすることが、強化学習での学習。

• 戦略は強化学習におけるモデルである。

※「戦略のパラメータを調整し」というのはどのようなパラメータなのか？

##報酬の総和の式

強化学習では報酬の総和の最大化を求めるので、報酬の総和の式を説明します。

MDPにおける報酬の総和は即時報酬の合計となる。

エピソードが時刻$T$で終わる場合、時刻$t$における報酬の総和$G_{t}$は以下のように定義されます
$G_{t}:=r_{t+1}+r_{t+2}+r_{t+3}+\ldots +r_{T}$

※しかし、この式のままには問題があり使えないので少し変えます。
問題：$G_{t}$はエピソードが終了しないと計算できない
解決：見積もりを立てる
だが見積もりは不確かなものであるため、割り引く必要がある
→割引率(Discount factor)$\gamma$を使うと

$G_{t}:=r_{t+1}+\gamma r_{t+2}+\gamma ^{2}r_{t+3}+\ldots + \gamma ^{T-t-1}r_{T}$
$=\gamma^{k}$$r_{t+k+1}$$\sum ^{T-t-1}_{k=0}$
※なぜかつなげるとバグってしまうため、$\gamma$ $r$を外に出しています、、、

• 割引率は0~1
• 将来の時刻になるほど割引率の指数が大きくなるため、つまり将来になるほど割引かれている。
• このように未来に得られる値を、割引率で割り引いた値を割引き現在価値という。

※感覚的に説明すると、明日もらえる10万と一年後もらえる10万円じゃ明日もえらたほうが嬉しいですよね。今もらえるものと将来のものでは価値が違うという人の考え方を導入しています。

##期待報酬(価値)とは
以上の式を再帰的な式で表すと

• 再帰的な式とは、$G_{t}$を定義する式の中で$G_{t}$を使うこと

$G_{t}:=r_{t+1}+\gamma r_{t+2}+\gamma ^{2}r_{t+3}+\ldots + \gamma ^{T-t-1}r_{T}$
$=r_{t+1}+\gamma\left(r_{t+2}+\gamma r_{t+3}+\ldots + \gamma ^{T-t-2}r_{T}\right)$
$=r_{t+1}+\gamma G_{t+1}$

• 期待報酬(価値)$G_{t}$とは

• この$G_{t}$「報酬の総和」を「見積もった値」を**期待報酬(Expected reward)、または価値(Value)**と呼ぶ。※以下の説明では価値を使う

• 価値を算出することを**価値評価(Value approximation)**という。
• この価値評価が強化学習で学習する2つのもの１つである**「行動の評価方法」**である。

##迷路移動におけるMDPの構成要素

• 状態 $s$：座標、マス目、セルなどの現在の位置
• 行動 $a$：上下左右へ移動すること(迷路だから上下左右四方向しかない)
• 遷移関数 $T$：状態 $s$と行動 $a$を受け取り、移動可能なセルとそこへ移動する確率(遷移確率$P_{a}$)を返す関数

• つまり、元の位置(状態$s$)とどの方向へ行くか(行動$a$)から
• →移動した場合の位置(遷移先$s'$)と本当に移動するかの確率(遷移確率$P_{a}$)が得られる
• 右へ移動しようとして、右へ移動できる確率
• ※実際に移動しない、もしくは違う方向に移動してしまう場合がある。例えば、床が滑っている、強風が吹いているため違う方向に移動してしまうなど。

• 即時報酬$R$：状態$s$と遷移先$s'$を受け取り、報酬$r$を返す関数。

• つまり、元の位置(状態$s$)と移動した場合の位置(遷移先$s'$)から報酬$r$を返す。
• 元の位置は何もないマス
• →遷移先がボーナスがあるマスなら$r$=+1
• →遷移先がペナルティがあるマスなら$r$=-1
• →遷移先が何もないマスなら$r$=0

#まとめ

• 環境開始から終了までの期間を1エピソード(Episode)とする

• 強化学習の目的：1エピソードで得られる報酬の総和を最大化する

• 強化学習モデルが学ぶこと
  1、行動の評価方法
  2、（評価に基づく）行動の選び方＝戦略

• MDPの4つの構成要素
  $s$：状態(State)
  $a$：行動(Action)
  $T$：状態遷移の確率(遷移関数/Transition function)
  状態と行動を引数に、遷移先(次の状態)と遷移確率$P_{a}$を出力する関数。
  $R$：即時報酬(報酬関数/Reward function)
  状態と遷移先を引数に、報酬を出力するような関数(行動を引数にとる場合も)

• $\pi$：戦略(Policy)状態を受け取り、行動を出力する関数
  戦略に沿って動く主体エージェント(Agent)と呼ぶ。

• $G_{t}$「報酬の総和」を「見積もった値」を**期待報酬(Expected reward)、または価値(Value)**と呼ぶ。

• 価値を算出することを**価値評価(Value approximation)**という。

• この価値評価が強化学習で学習する2つのもの１つである**「行動の評価方法」**である。

##参考資料

• 機械学習スタートアップシリーズ-Pythonで学ぶ強化学習-入門から実践まで

• https://github.com/icoxfog417/baby-steps-of-rl-ja
  ※上記の本の公式アカウントです。コードや概要が見れます。

• Math Webmemo手書きの公式をLaTex変換してくれます！マジおすすめ！