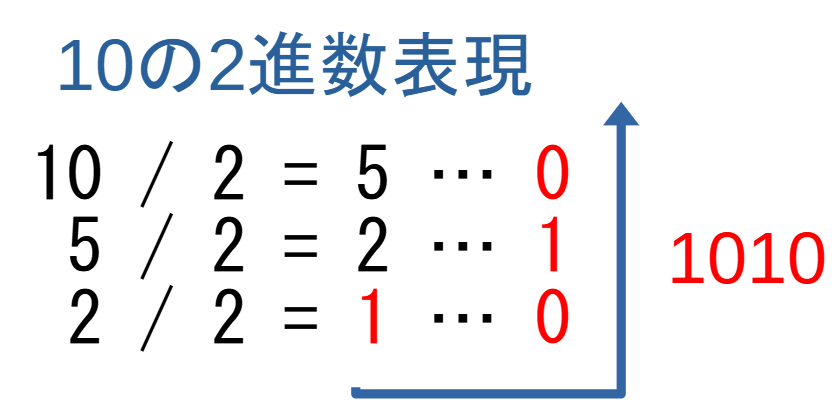
初めてAtCoderに参加してから約半年が経ちました.
毎週AtCoder Beginner Contest (ABC)に参加し, 勉強のために競プロ典型90問の★5以下を解きました.
半年間勉強して必要だった知識を, なるべくイラスト付きの解説とC++の実装と合わせて紹介します.
これだけ身につけると水色まで行けます.
※一部, 競プロ典型90問のネタバレ含みます
※C++17を想定してます
- 紹介する各種アルゴリズムの実装はこちら
- ABCで利用しているテンプレートはこちらのtemplate.cppです
- 競プロ典型90問を解いたコードはこちら
計算量
ABCでは, プログラムの実行時間の制限として2sや3sといった制限があります.
$10^8$のループでだいたい1sくらいだと思っておくと良いでしょう.
$n=10^5$なら, $n^2$のアルゴリズムではTLEとなってしまい, 正解になりません.
$n\log n$くらいまでのアルゴリズムで解く事が多いです.
一方で, $n=20$と小さい場合は, 全探索して$2^n(=1048576)$のアルゴリズムで解く場合もあります.
問題の制約を見て, ある程度やれることとやれないことを見極める必要があります.
オーダー記法の詳しい話はAtCoder公式解説があるのでそちらに任せます.
データ構造
問題を解く際にデータ構造の理解は必須です.
どれを使ったら実行時間に収まるかを考えながら解くことになります.
基本編
C++のコンテナクラスにも含まれる基本的なデータ構造について説明します.
基本的な事が多いので読み飛ばしてもらっても構いませんが, 詳しく調べてみると知らないことも多々ありました.
vector: 配列
超基本ですが, 性質は理解しておく必要があります.
vector<int> v(n); // 要素数nの1次元配列
vector< vector<int> > v2(m, vector<int>(n)); // m x nの2次元配列
- O(1)でランダムアクセス(
v[i])と末尾要素の削除(v.pop_back())可能 - 末尾への挿入(
v.push_back(x),v.emplace_back(x))はメモリ確保されていればO(1)- メモリ再確保が必要な場合はO(n)
- 事前にサイズがわかっている場合は
reserveでメモリ確保しておくべき
- 末尾以外への挿入は要素をずらす必要があるためO(n)
競プロでは真ん中に挿入したり, 1つ後ろにずらしたくなるケースがありますが, たいてい違うデータ構造を用いるか, 参照するindex側をずらすことで対応できます.
例題: 044 - Shift and Swapping(★3)
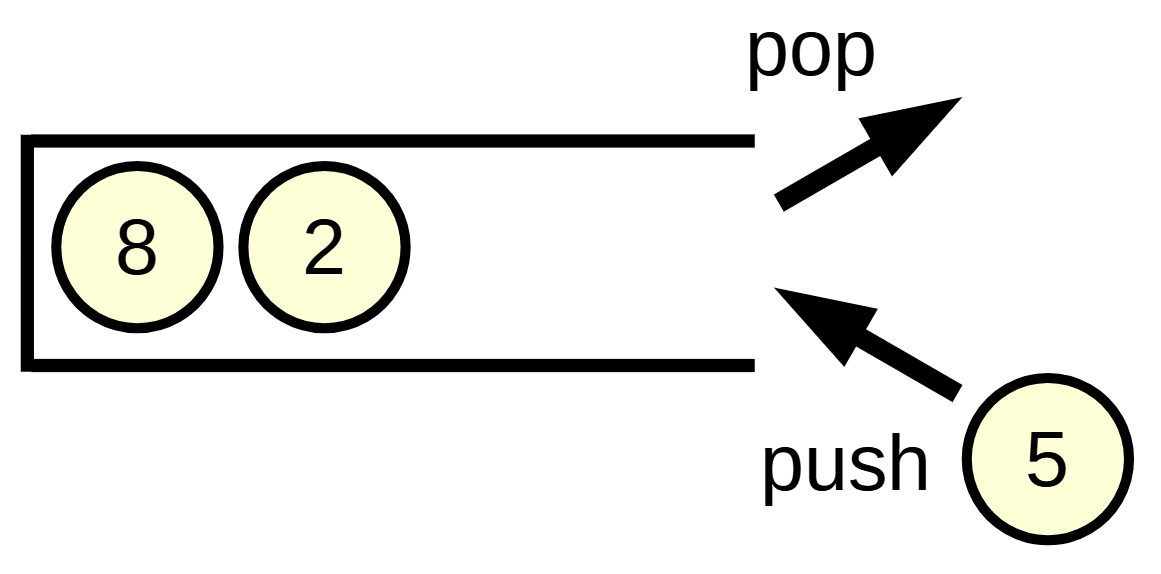
queue: キュー
queue<int> q;
q.push(3); // 末尾に要素追加
int f = q.front(); // 先頭要素参照
q.pop(); // 先頭要素削除
- O(1)で先頭要素の参照(
q.front())と削除(q.pop()), 末尾への追加(q.push(x))が可能 - 幅優先探索(BFS)でよく使われる (後述)
- このような先入れ先出し構造をFirst In First Out (FIFO)と呼びます
競プロでは, 必要となるものをpushしておいてキューがなくなるまでループし(while(!q.empty())), 後で処理していくというような使い方をよく行います.
例題: ABC226 C - Martial artist
公式解説ではグラフを用いていますが, キューを使って解くことができます.
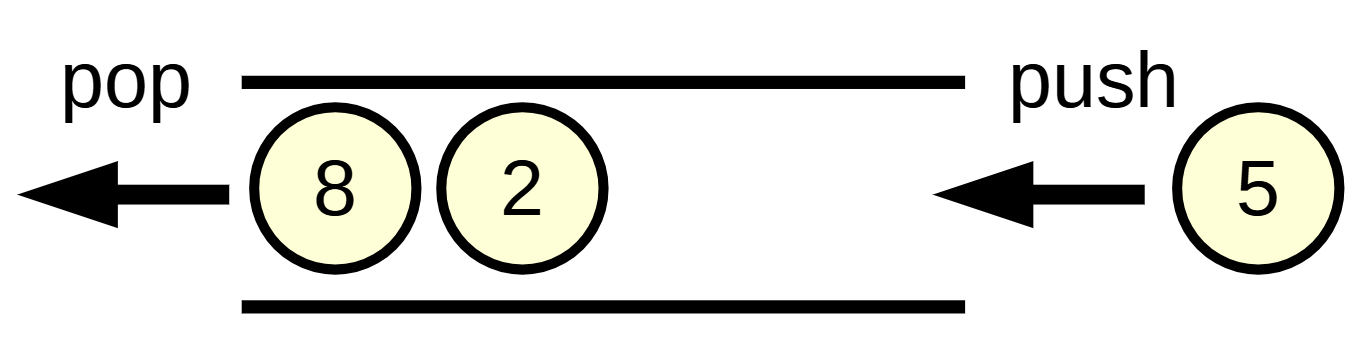
stack: スタック
stack<int> st;
st.push(3); // 要素追加
int t = st.top(); // 次に取り出される要素の参照
st.pop(); // 最後に入った要素を削除
- O(1)で入り口の先頭要素の参照(
st.top())と削除(st.pop()), 要素追加(st.push(x))が可能 - 深さ優先探索に使われる (後述)
- 最後に入った要素が最初に出るため Last In First Out (LIFO) と呼ばれます
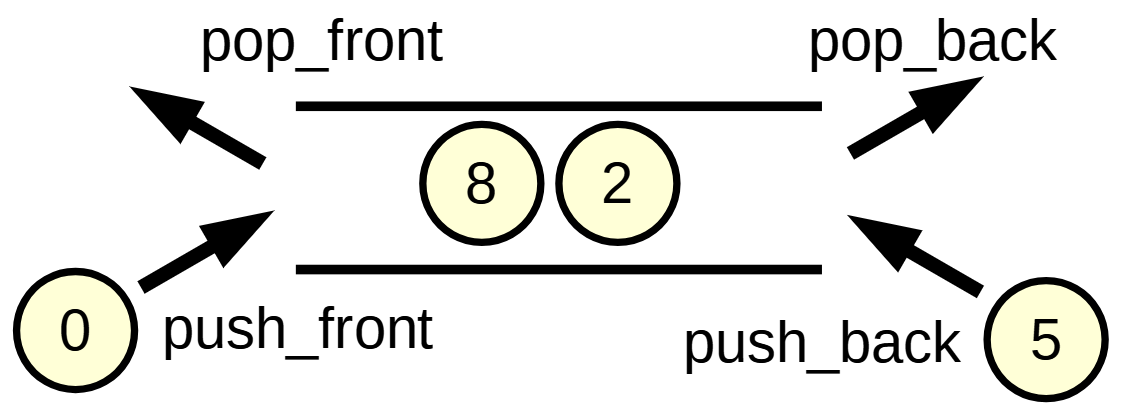
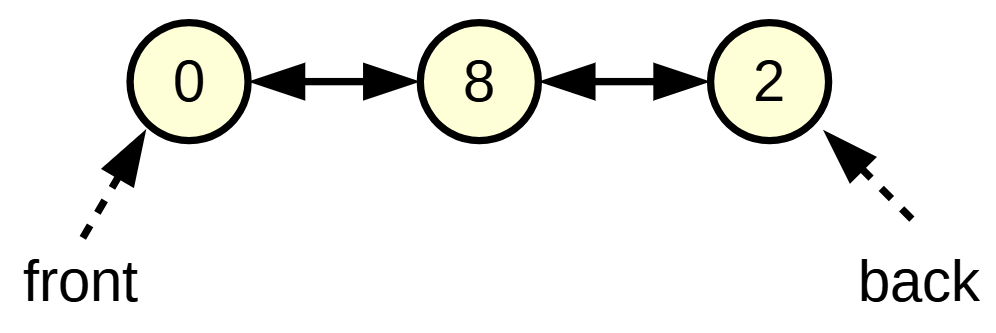
deque: 両端キュー
deque<int> deq;
deq.push_front(3); // 先頭に要素追加
deq.push_back(0); // 末尾に要素追加
int f = deq.front(); // 先頭要素取得
deq.pop_front(); // 先頭削除
int b = deq.back(); // 末尾要素取得
deq.pop_back(); // 末尾削除
- O(1)で先頭/末尾への追加(
deq.push_front(x)/deq.push_back(x)), 削除(deq.pop_front()/deq.pop_back()), 参照(deq.front()/deq.back())を行えます - 途中への挿入はO(n)なため基本行いません
- 01BFSに使われます(後述)
C++のdequeはランダムアクセスもO(1)で可能です.
一方でpythonのfrom collections import dequeはランダムアクセスがO(n)なため注意が必要です.
例題: 競プロ典型90問 061 - Deck(★2)
この問題は, 配列の開始インデックスと終了インデックスを自分で管理して末尾追加と先頭追加を自分で行うのが普通ですが, C++のdequeがランダムアクセスO(1)であることを知っていると, 少し楽になります.
priority_queue: 優先度付きキュー
常に最大値 (または最小値)を取り出せる構造です.
priority_queue<int> pq;
pq.push(3); // 挿入
int maxval = pq.top(); // 最大値を取得
pq.pop(); // 最大値を削除
- O(1)で最大値を取得(
pq.top())できる - O(log(n))で挿入(
pq.push(x))と最大値の削除(pq.pop())を行えます - 常に最小値を取得したいときは
priority_queue< int, vector<int>, greater<int> >で宣言する
競プロでは, 最適性を満たしつつ処理したいことがよくあるため, よく使われます.
例題: ABC214 C - Distribution
ダイクストラ(後述)でも使われます.
競プロをやるにはこれだけ知っておけば十分ですが, 実装方法も知っておいて損は無いと思います.
実装には二分ヒープ木がよく使われます.
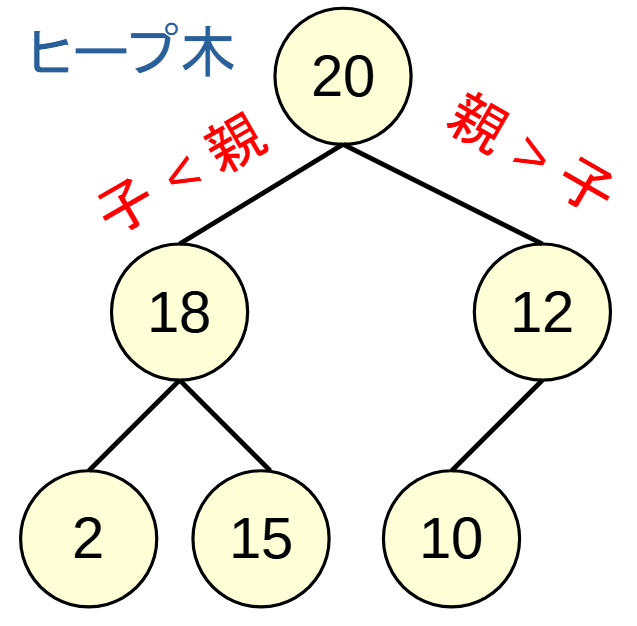
-
親の値 > 子の値を維持した木構造です - 根が常に最大値となります
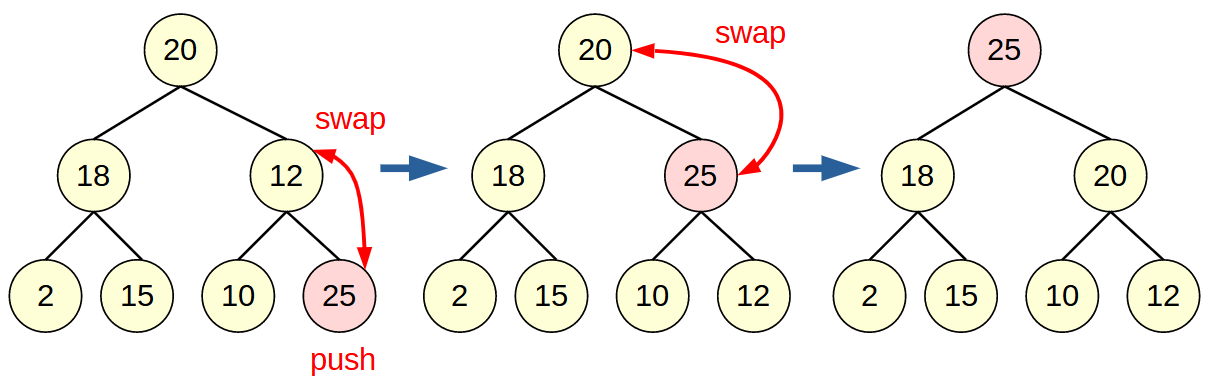
新しく要素を挿入する際は, 新しい葉を付けた後に親 > 子の条件を満たさない間だけ交換していくことで, ヒープ構造を保てます. 交換は最大でも木の高さ分なのでO(log(n))で行えます.
最大値を取り出した際は, 葉にあった値を根に持ってきてから, 左右の子のうち, 大きい方の子と交換していくことで, ヒープ構造を保てます. 同様にO(log(n)).
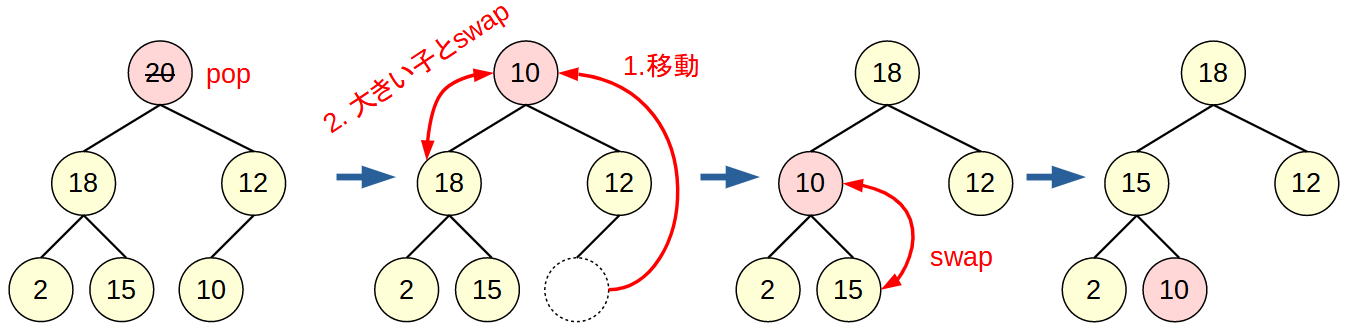
イラストでは木で表しますが, 配列で実装されます.
二分木になるため, 親data[i]に対して, 子はdata[2*i+1],data[2*i+2]で表せます.
ヒープ構造はソートアルゴリズムであるヒープソート(nlog(n))にも使われています.
list: 双方向リスト
list<int> ls;
ls.push_back(3); // 先頭に要素追加
auto it = ls.begin();
ls.insert(it, 2); // itの位置に挿入
- 任意の箇所への挿入(
ls.insert(it, x))と削除(ls.erase(it))がO(1)で行える (挿入位置のポインタを持っている必要がある)- ポインタを付け替えるだけなため
- ランダムアクセスは順にたどっていくしかないためO(n)です
pythonのlistは配列のことで, この双方向リストのことではないため注意.
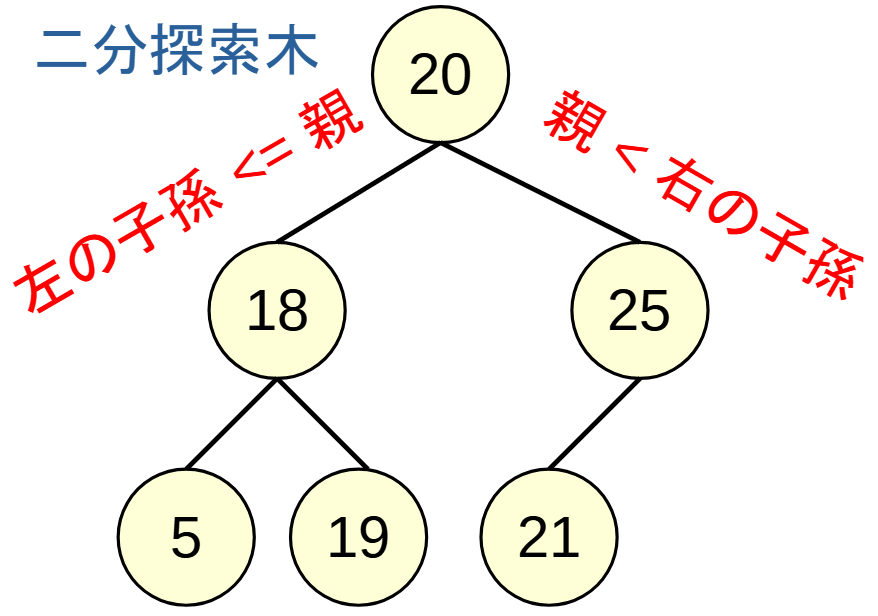
set: 集合, 平衡二分探索木
set<int> s;
s.insert(2); // 2を挿入
auto it = s.find(2); // 2を探す it != s.end() なら存在
s.erase(2); // 2を削除
内部では左の子孫<=親<右の子孫を保つような二分木で管理される.
木のアンバランスを解消するため, 挿入や削除の際に木をバランスさせる平衡二分探索木 (赤黒木, AVL木など)で実装される.
- 集合への挿入(
s.insert(x)), 削除(s.erase(x)), 検索(s.find(x))がO(log(n))で行える - x以上の要素を探索できる
s.lower_bound(x), xより大きい要素を探索できるs.upper_bound(x)を持つ-
#include<algorithm>にあるlower_bound(s.begin(), s.end(), x)を使うより, メンバ関数のs.lower_bound(x)を使ったほうが圧倒的に速い
-
ちなみに, 重複を許すmultisetというものもあります.
map: 連想配列, 辞書
map<int, int> m;
m[10]=3; // 10に3を格納
m[2]++; // 2に1を加算 (初期値は0なため1になる)
m.erase(2); // 2を削除
keyに対するvalueを格納するデータ構造. 内部では集合と同じ構造で持っている.
- keyの削除(
m.erase(x)), keyの格納(m[x]=val), keyの検索(m.find(x))がO(log(n))で行える - valueの検索は全探索するしかないためO(n)
c++のmapは, 値がなくても加算できるpythonのfrom collections import defaultdictのような動作をします.
書き込まなくてもm[x]で参照するだけでデフォルト値が格納されるため, 存在確認を行う場合はm.find(x)を使う必要があります.
応用編
基本編は, 情報工学学生なら大学でも習うような内容なので, 知っている人は多いと思います.
ここからは私がAtCoderを始めてから知ったデータ構造を紹介します.
Union Find
Union Findはグループ分けを木構造で管理するデータ構造です.
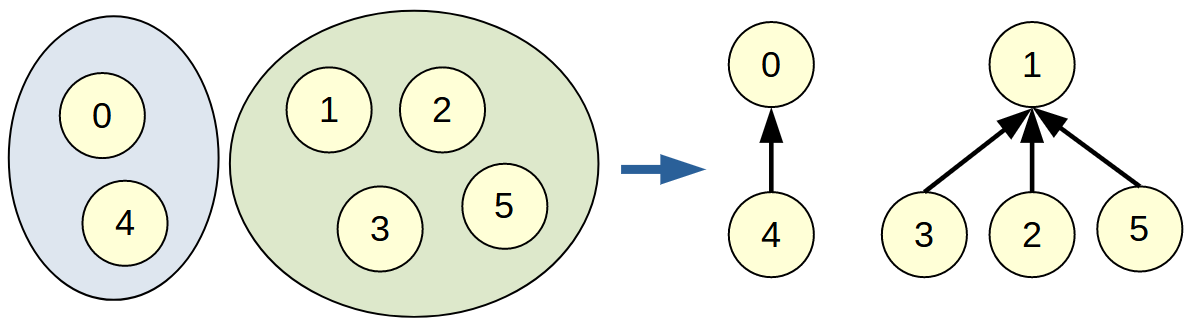
このように互いに共通部分を持たない集合 (素集合)を扱います.
Union Findの考え方: 同じ根を持つなら同じグループに属する
以下を高速に行うことができます.
- xとyが同じ集合かどうかの判定
- xが属する集合とyが属する集合をつなげる
連結判定によく使われます.
例題: 競プロ典型90 012 - Red Painting(★4)
いろんな方が実装を公開されていますが, 私は最初pythonでやっていたこともあり, この方の実装を見て, C++で書きました.
class UnionFind {
private:
int n;
vector<int> parent; //親のノード情報、自身が根の場合はその集合のサイズを負で持つ
public:
UnionFind(int n) : n(n), parent(n, -1){} // -1で初期化
// データxが属する木の根
int root(int x) {
if (parent[x] < 0) return x;
return parent[x]=root(parent[x]);
}
// xとyの木を併合
void merge(int x, int y) {
x = root(x);
y = root(y);
if (x == y) return;
if (parent[x] > parent[y])
swap(x, y);
parent[x] += parent[y]; // 個数更新
parent[y] = x; // 根の付け変え
}
// 同じ木に属するかどうか
bool same(int x, int y) {
return root(x) == root(y);
}
// xの集合のサイズ
int size(int x) {
return -parent[root(x)];
}
};
実装は親を表す配列を使って行います.
自身が根の場合は負の値を持ち, 集合のサイズをマイナスで表すことにします.
最初は{0},{1},{2}, ..., {n-1}の状態から始まるため, 配列の要素はすべて-1です.
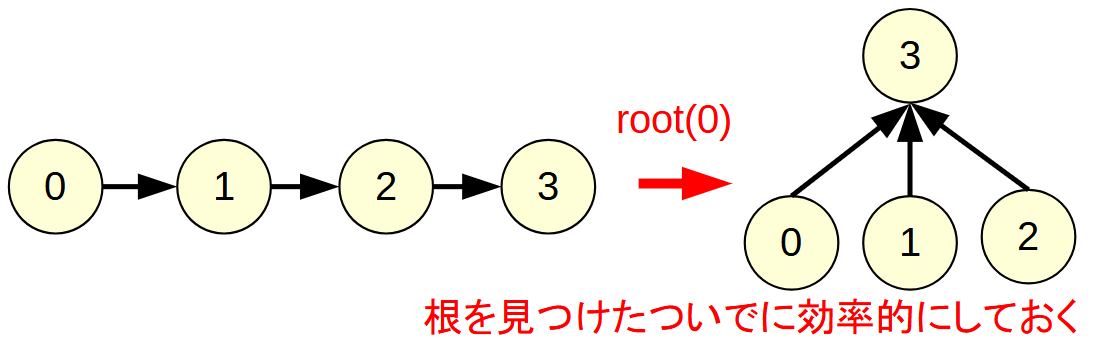
xの根を求めるroot(x)は, 再帰的に親をたどっていけばよいだけです.
parent[x]=root(parent[x])としているのは, 根を見つけるついでに, 木構造を整形するためです.
merge(x,y)はrootで根を見つけた後に, 片方の根をもう一方の根にリンクを張るだけです.
このとき, 大きいサイズの木に小さいサイズの木をつなげるようにしています.
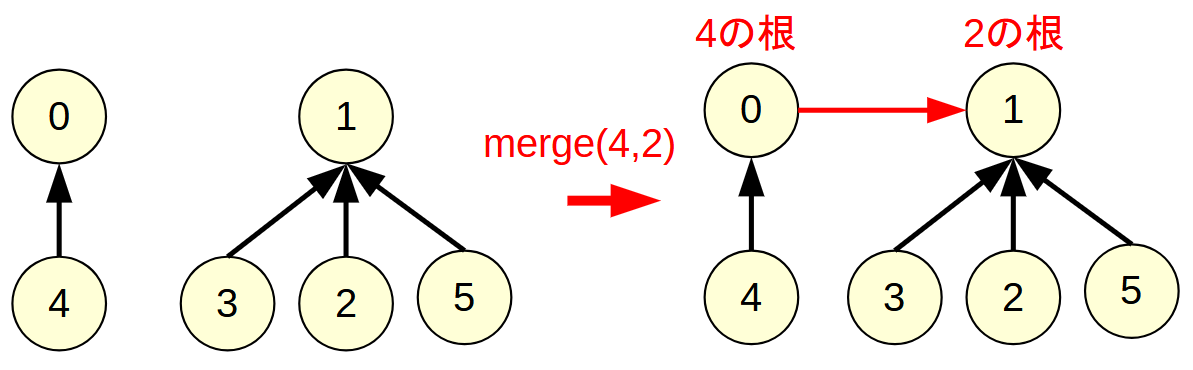
same(x,y)は同じ根を持つかどうかを返していて, 集合のサイズsize(x)は根のマイナスの値で取得できます.
この他に
- xの属する集合の要素列挙
- 根の列挙
- 木の数
- すべての要素の可視化
の実装はこちらにおいておきます.
Segment Tree
区間の最小値や合計値を効率的に求められるデータ構造です.
- 任意の区間の最小値(or 最大値 or 合計値)などを求めれる
- 値の更新
をO(log(n))で行うことができます.
完全二分木の葉に, 区間の各値に対応する値を格納します.
以下は, 区間の最大値を効率的に求めるSegment Treeの例です.
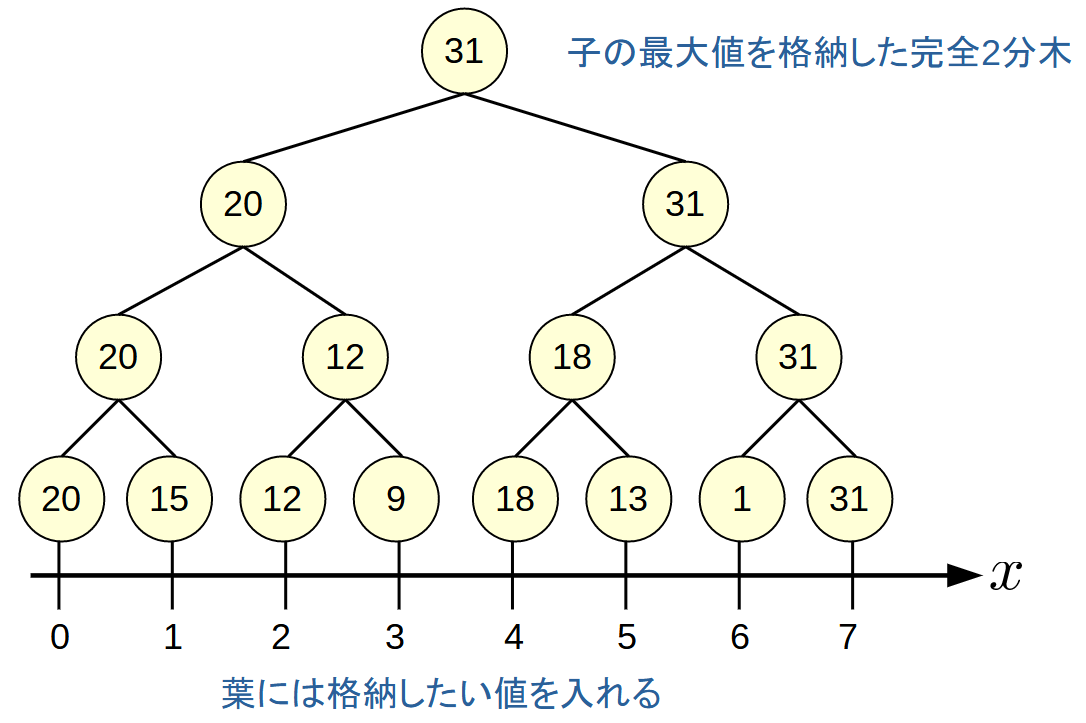
親は子の最大値を持つようにします.
区間の最大値を求める
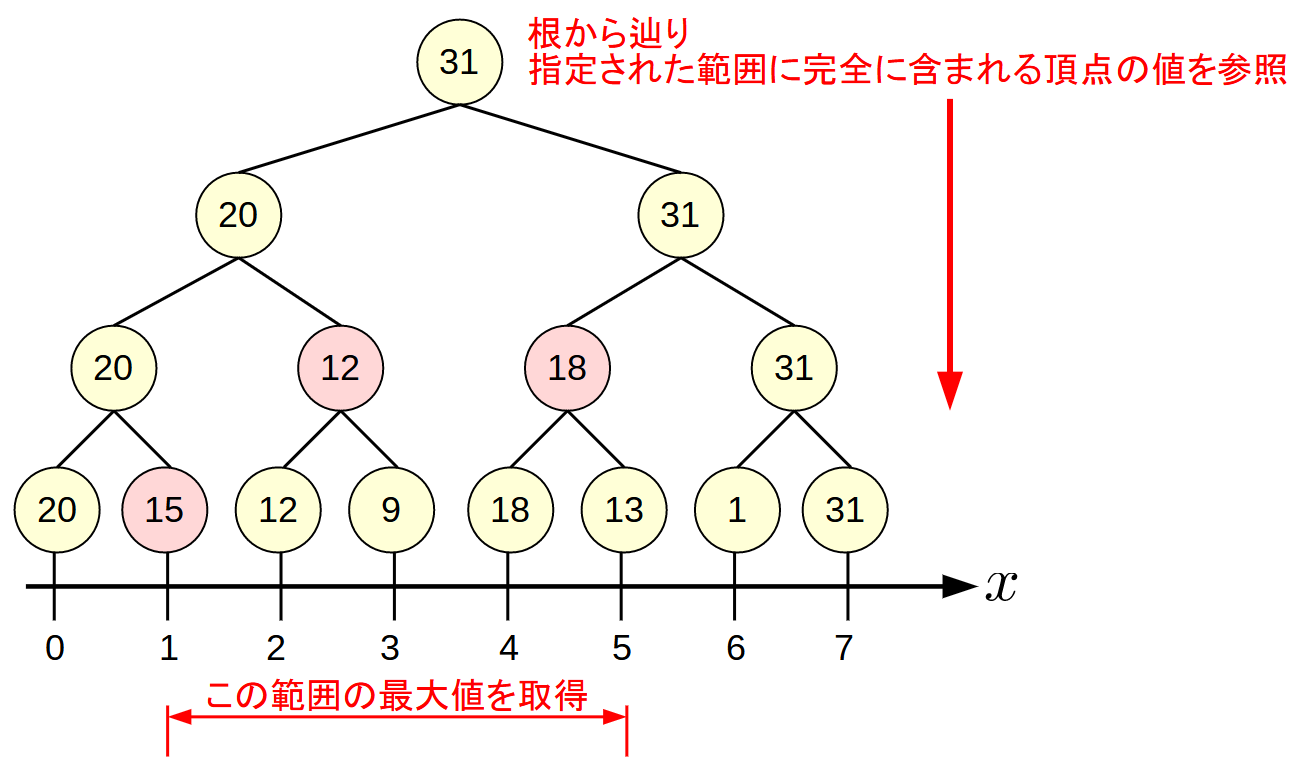
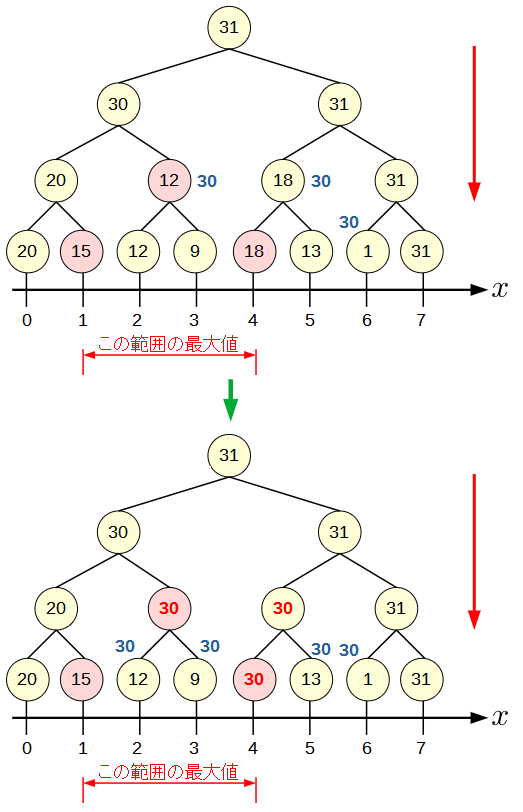
たとえば, 区間[1,5]の最大値を求める手順は, 根から辿っていき, 各頂点に対応する範囲が求めたい範囲[1,5]に含まれる箇所の値のmaxが求めたい最大値になります.
この例では, [1], [2,3], [4,5]に対応する15, 12, 18の3つのうちmaxである18です.
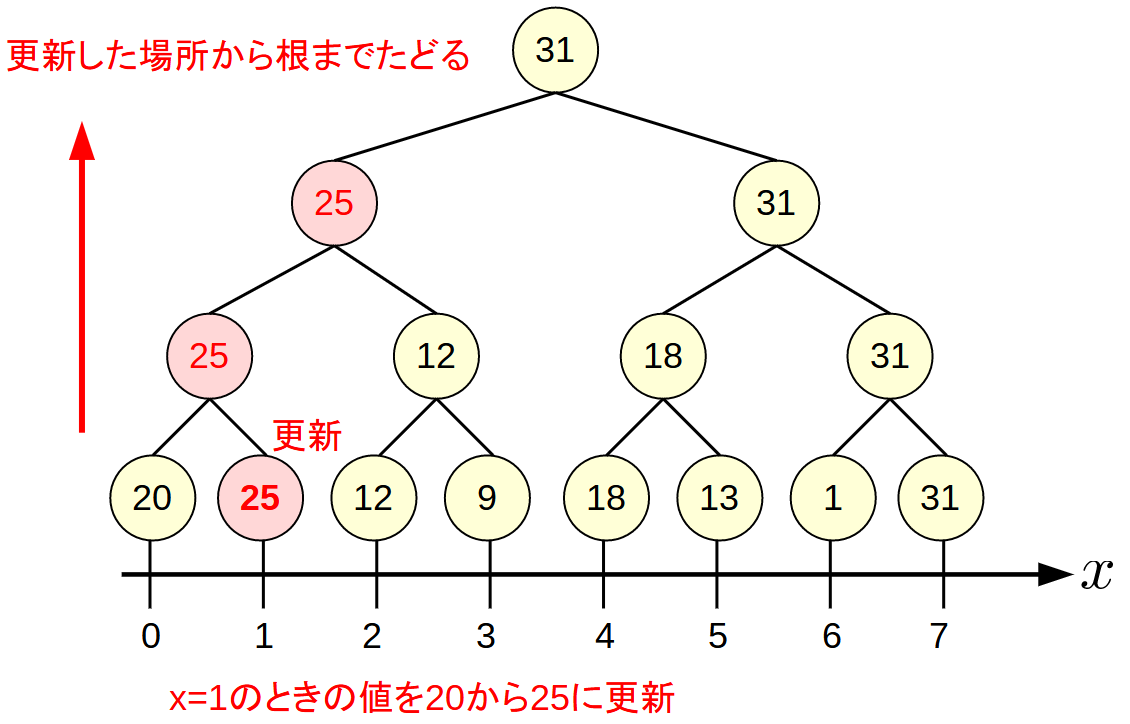
値の更新
x=1の値を25に変更する手順は, 更新した箇所から根に向かって値を更新していくだけです.
区間の値を同時に更新
1つの値を更新するなら先程の方法で良いですが, 区間の値を更新する場合は効率が悪いです.
[2,6]の値を30に更新する例:
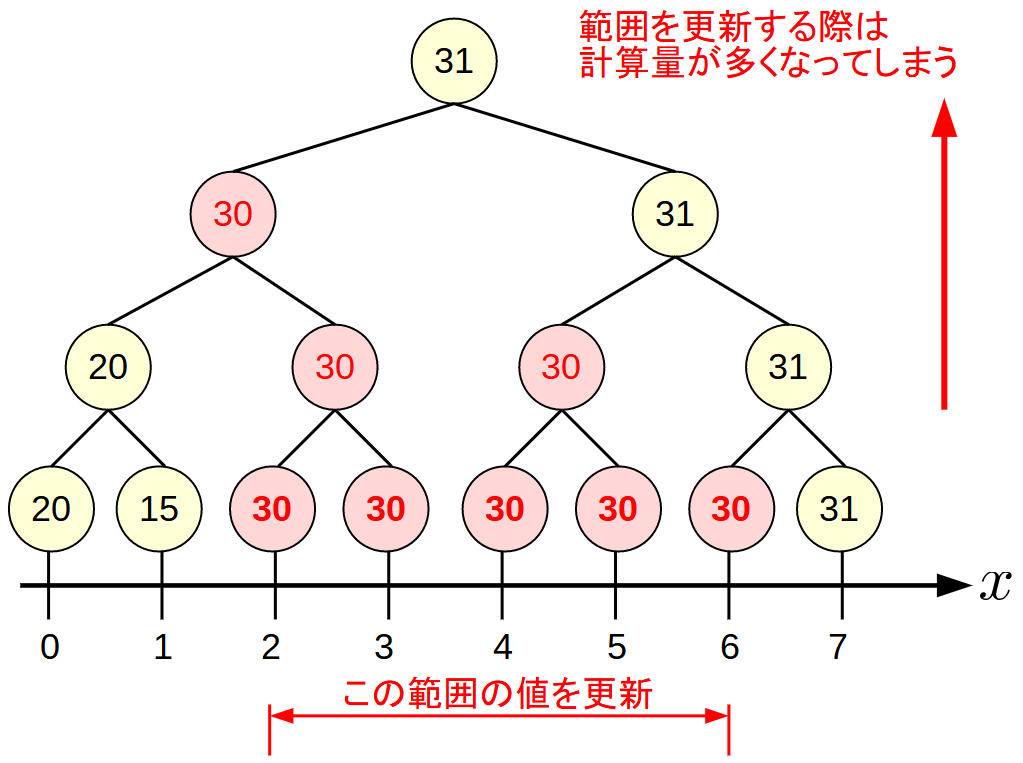
その対策には遅延評価が使われます.
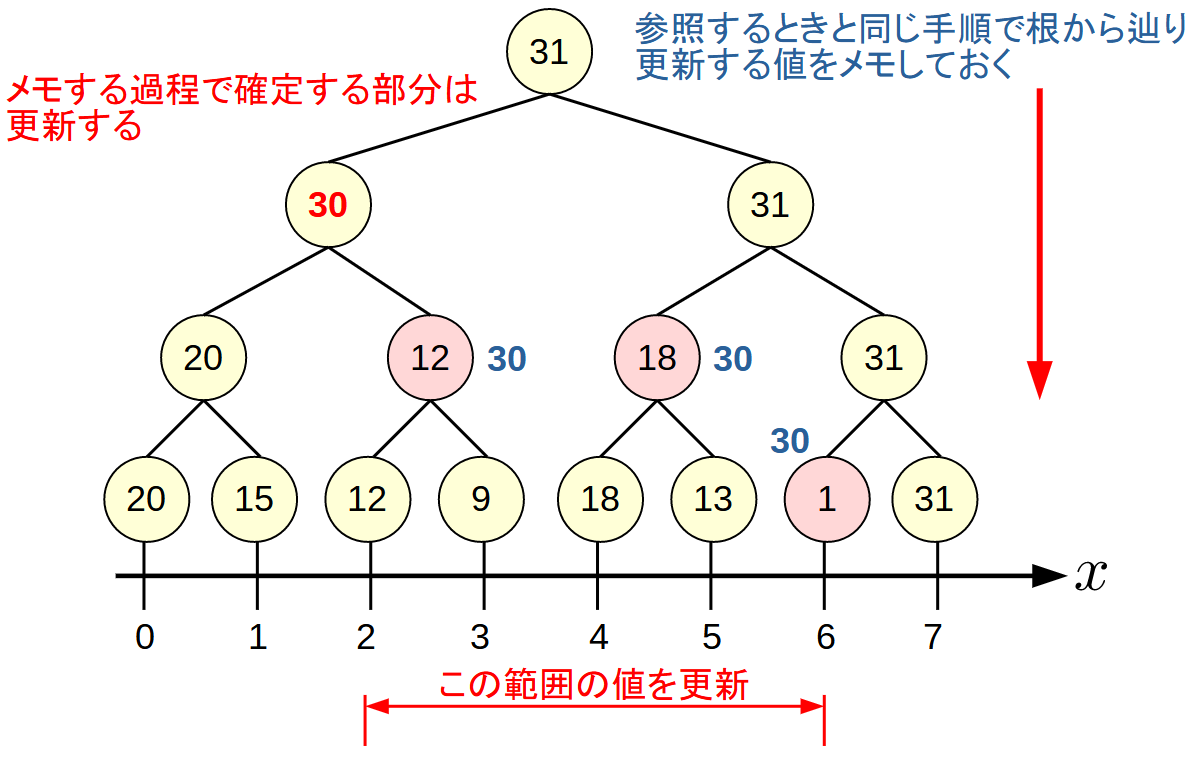
最大値を求める手順とおなじように更新区間に含まれる頂点に更新すべき値をメモしておきます. (青色部分)
実際に更新されるのは参照された際に行われます.
たとえば,[1,4]の範囲の最大値を求めたいときには, 赤色の頂点を見る際に, その値を更新すると同時に子ノードにメモを伝えます.
例題: 競プロ典型90問 029 - Long Bricks(★5)
Segment Treeの実装もいろんな方が公開してますが, この方の実装を参考に, 少し変更を加えました.
// 最大値に関するセグメント木
template <class T>
class SegmentTree {
private:
T init_val; // 初期値
int num_leaves; // 葉の数 (2のべき)
vector<T> data, lazy;
vector<bool> upd; // 更新があるかどうかフラグ
T op(T a, T b){
return max(a, b); // ここを書き換えれば最小値や合計値に対する木も作れる (ただし合計値の場合, 区間の同時更新は無理)
}
void __update(int a, int b, T val, int i, int l, int r) {
eval(i);
if (a <= l && r <= b) { // 範囲内のとき
lazy[i] = val;
upd[i] = true;
eval(i);
} else if (a < r && l < b) {
__update(a, b, val, i * 2 + 1, l, (l + r) / 2);
__update(a, b, val, i * 2 + 2, (l + r) / 2, r);
data[i] = op(data[i * 2 + 1], data[i * 2 + 2]);
}
}
T __query(int a, int b, int i, int l, int r) {
eval(i);
if (r <= a || b <= l) // 範囲外のとき
return init_val;
if (a <= l && r <= b)// 範囲内のとき
return data[i];
T vl = __query(a, b, i * 2 + 1, l, (l + r) / 2);
T vr = __query(a, b, i * 2 + 2, (l + r) / 2, r);
return op(vl, vr);
}
void eval(int i) {
if (!upd[i]) return; // 更新が無ければスルー
if (i < num_leaves - 1) { // 葉でなければ子に伝播
lazy[i * 2 + 1] = lazy[i];
lazy[i * 2 + 2] = lazy[i];
upd[i * 2 + 1] = true;
upd[i * 2 + 2] = true;
}
// 自身を更新
data[i] = lazy[i];
lazy[i] = init_val;
upd[i] = false;
}
public:
SegmentTree(int n, T init) {// [0,n)の範囲を持つセグメント木
int x = 1;
while(n > x)
x *= 2;
num_leaves = x;
init_val = init;
data.resize(num_leaves*2-1, init_val);
lazy.resize(num_leaves*2-1, init_val);
upd.resize(num_leaves*2-1, false);
}
void update(int a, int b, T val) {// [a,b)区間の値をvalに更新 (ただし合計値の木には使えない)
__update(a, b, val, 0, 0, num_leaves);
}
void update(int i, T val) {// 値を更新
__update(i, i+1, val, 0, 0, num_leaves);
}
T query(int a, int b) {// [a,b)の最大値を取得
return __query(a, b, 0, 0, num_leaves);
}
T query(int i) {// iの最大値を取得
return __query(i, i+1, 0, 0, num_leaves);
}
};
更新があるかのフラグupdを明示的に持たないと, AtCoderで不正解になる場合(初期値と更新したい値が同じ場合)があったため, 明示的に持ってます.
また, 使いやすさのために単体の値を更新する関数も持たせました.
合計値を扱うSegmentTreeでは、区間代入の代わりに、区間加算を行えます。実装はこちらにあります。
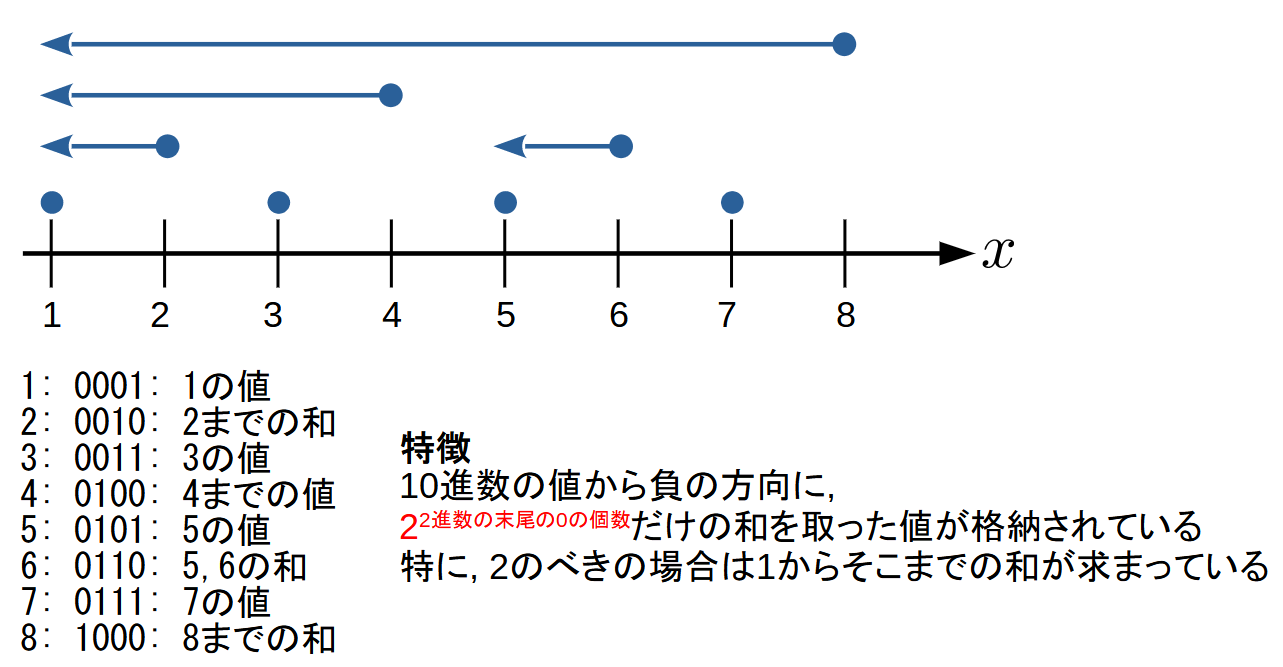
Binary Indexed Tree (BIT)
セグメント木では任意の区間について求める事ができましたが, BITでは, 以下の2つの機能に限定されます.
- 最初からi番目までの和
- i番目にxを加算
特徴
- 1始まりのindexで持った配列で管理:
data[x] -
data[x]には$(x-2^{k}, x]$区間の和が格納されています- ただし, $k$は$x$を2進表記したときの末尾の0の個数
iまでの和を求める
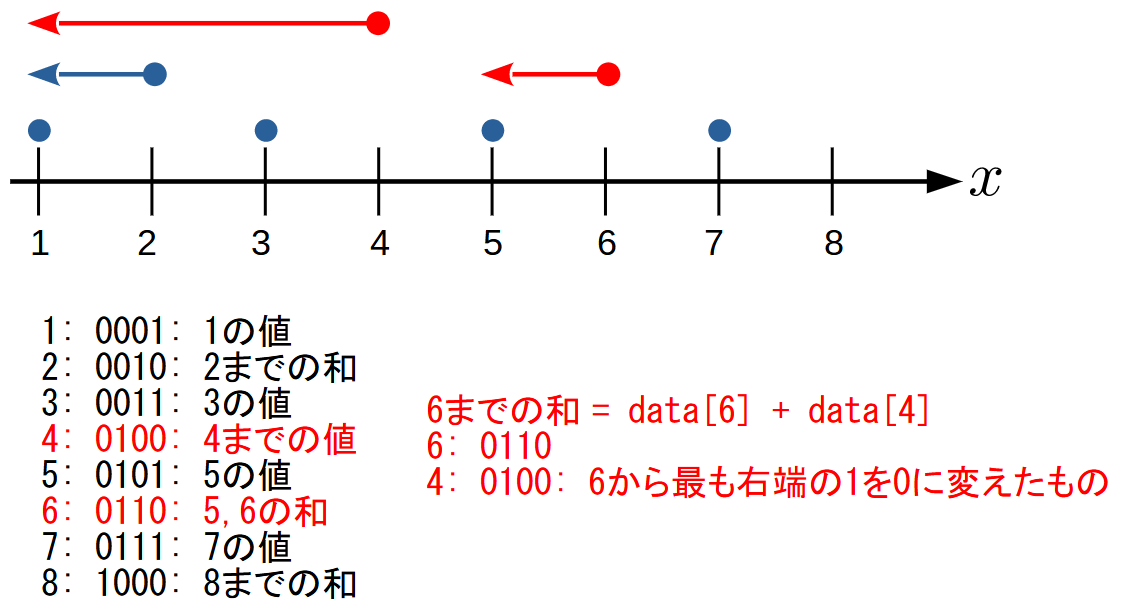
たとえば, 6までの和はdata[6]+data[4]で求まります.
この6から4はどう求まるかというと, 2進数表記したときの最も右端の1を0に変えると4になります.
これは, 特徴で挙げた性質を考えると理解できると思います.
i番目にxを加算
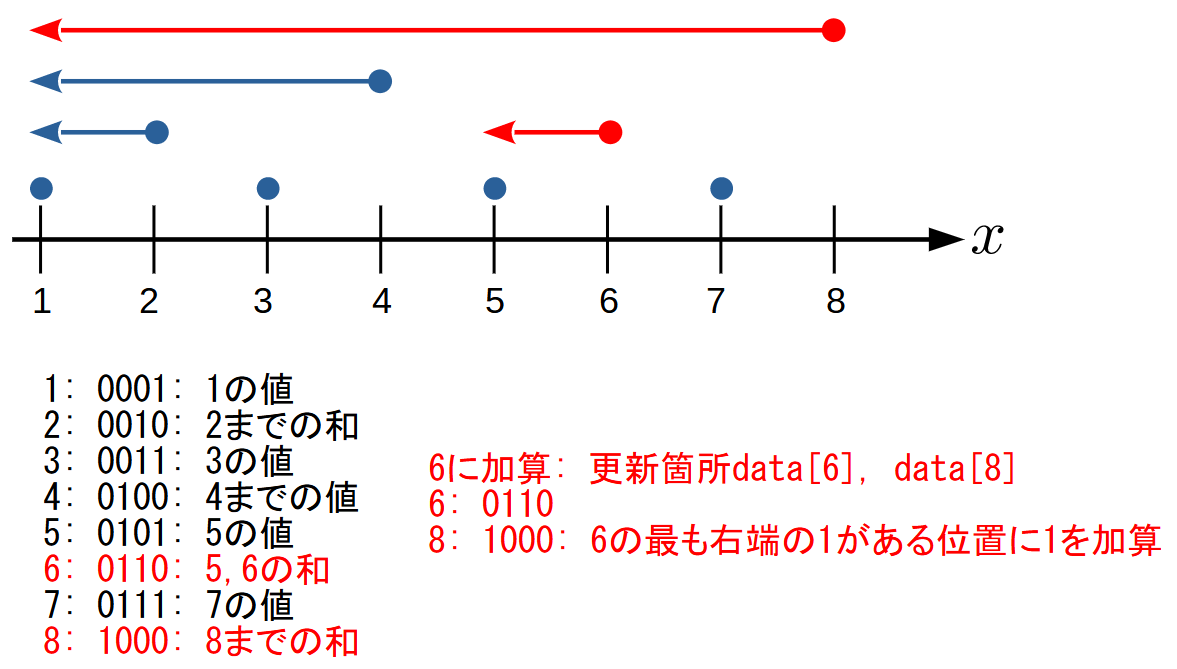
6番目にある値を加算する場合, 6番目の和を含むdata[6]とdata[8]を更新する必要があります.
この6から8は, 2進数表記したときの最も右端にある1に1を加算することで求まります.
以上のように, 2進数演算を利用することで, 足す対象を求めていくことができます.
どちらも場合も, 最も右端にある1を求める必要がありますが, i & -iで求めることができます.
これは-iがビット反転+1という表現をしているためです.
01010000 = i
10101111 = iのビット反転
10110000 = -i
00010000 = i&-i
template <class T>
class BIT {
int n;
vector<T> bit;
public:
BIT(int _n) : n(_n + 1), bit(n, 0) {}
// a[i] += val ただし i in [0, n)
void add(int i, T val) {
for (int idx = i+1; idx <= n; idx += (idx & -idx))
bit[idx] += val;
}
// a[0] + ... + a[i] ただし i in [0, n)
T sum(int i) {
T s(0);
for (int idx = i+1; idx > 0; idx -= (idx & -idx))
s += bit[idx];
return s;
}
};
機能を限定している分, 実装が軽くセグメント木よりも計算量が定数倍早いです.
説明では1始まりのインデックスでしたが, 配列と同様に0始まりに統一したいため, 利用するユーザー側には1始まりであることを意識しないようにしてます.
動的計画法 (Dynamic Programming: DP)
ナップサック問題の解法で有名ですが, いざ他の問題をやろうと思うと難しいと感じる人も多いと思います.
それはナップサック問題が2次元のDPで複雑だからだと思います.
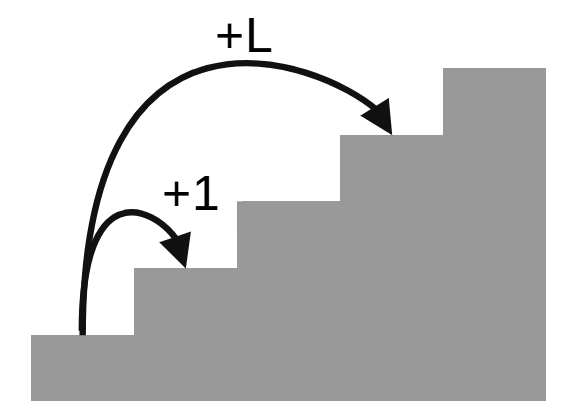
まずは1次元のDPで理解してみよう.
例題: 競プロ典型90問 050 - Stair Jump(★3)
- $N$段の階段を上る ($N\le 100000$)
- 一歩で1段か$L$段上ることができる ($L\le 100000$)
- 0段目から出発し, N段目にたどり着くまでの移動方法は何通りあるか?
- ただし, $10^9+7$で割った余りで答える
DPという大層な名前がついていますが, 基本的には漸化式を立てるだけです. (そこが難しかったりしますが...)
これを意識するだけで, DPをある程度書けるようになると思います.
- 段ごとに答えを格納する
dpという配列を用意します- 段は0からNまであるため, N+1のサイズあれば十分です
- 漸化式を立てます
- i番目の段は「i-1段から1段上がって来るパターン」と「i-L段からL段上がってくるパターン」の2つの和で表せます
dp[i] = dp[i-1] + dp[i-L]- (オーバーフローしないように
dp[i]を$10^9+7$の余りにする)
- 漸化式の初項を求めます
-
dp[i] = 1($0\le i<L$のとき1段ずつ上がってくるしかない)
-
- ボトムアップ式に下から順に求めていきます
- $i=L, L+1, \ldots, N$の順に2.の漸化式を利用していきます
このように, 漸化式を立てて小さい部分問題から順番に埋めていくことで問題を解くことができました.
DPの実装方法には, 今説明したボトムアップ方式の他に, トップダウン方式で再帰探索中に計算結果を記録しておき, 同じ問題を解くときに記録しておいた結果を返し, 計算をスキップするメモ化再帰もあります.
2次元配列の場合も同じように漸化式を立てて, 順番に更新していくことで, DPを行うことができます.
配るDPと貰うDP
DPの書き方には配るDPと貰うDPがあります.
先程の階段の例では, 過去の結果から現在求めたいiの答えを貰うので貰うDPと呼ばれます.
dp[i]+=dp[i-1]dp[i]+=dp[i-L]
一方で, i番目から遷移先の値を更新する書き方を配るDPと呼びます.
dp[i+1]+=dp[i]dp[i+L]+=dp[i]
問題によって書きやすい方で書くとよいです.
添字と値を入れ替えるDP
よく行うDPでは, dp[c]=コストc以下ときの価値vの最大値というように, 求めたい答えを配列の値に格納しますが, 逆にdp[v]=価値vを得るのに必要なコストcの最小値とすることで, 効率的に解ける場合があります.
参考: LIS でも大活躍! DP の配列使いまわしテクニックを特集
木DP
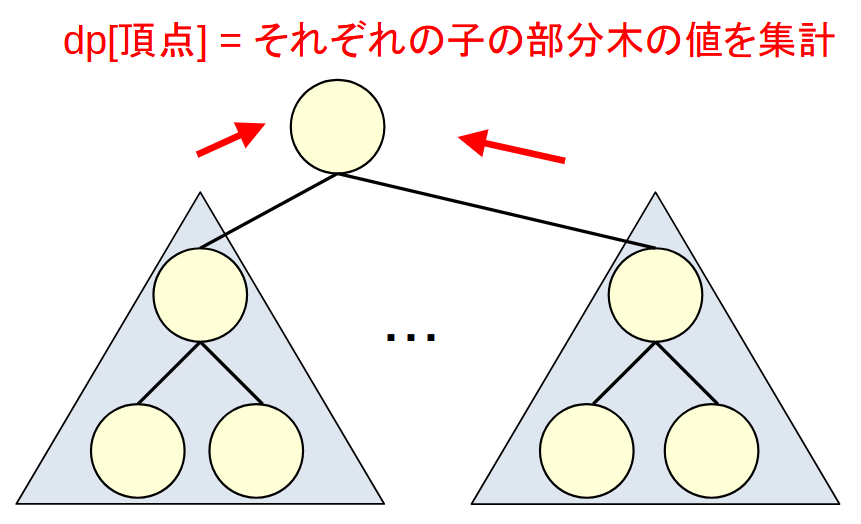
深さ優先探索で潜っていき, 戻ってきた際に, 各部分木の結果を集計して行う木DPもあります.
配列から木に変わっただけで, 本質は変わりません.
例題: 競プロ典型90問 073 - We Need Both a and b(★5)
bitDP
集合をビット列で表して扱うdpです.
集合$S$に対して,
$$
\mathrm{dp}[S\cup \{i\}] = \mathrm{dp}[S] + S\text{と}\{i\}\text{をつなぐコスト}
$$
$S$の$i$ 番目のビットが1なら, 集合$S$に$i(=0, 1\ldots)$が含まれると考えます.
ビット演算を使って, 次のように表すことができます.
- 集合に$i$を追加:
S=S|(1<<i) - 集合に$i$が含まれるか:
S&(1<<i)または(S>>i)&1
桁DP
整数を桁ごとに見るDPです.
1からNまで通常のループで回しきれないくらいNが大きい場合に使います.
たとえば, N=24957の場合, N以下の整数は以下のようにグループ分けできます.

上位桁から見ていくため, 考え方としては,
dp[i] = 上位i桁目まで確定したときの暫定スコアの最適値
としますが, これだけでは不十分です.
たとえば, 上位3桁目まで決めたときに248XYの場合はXYはどんな数字が入ってもNを超えません. 一方, 249XYの場合はXYが57以下にする必要が出てきます.
ということで, もう一次元増やして考えます.
dp[i][smaller] = 上位i桁目まで確定したときの暫定スコアの最適値
ただし, 上位i桁目までを比較したときに,
- smaller=trueならN未満の場合
- smaller=falseならNと等しい場合
を考える.
dpのテーブルの形式が定まったので, 漸化式のパターンを考えます.
- i桁目まででN未満と確定したdp[i][true]の場合, 次の桁は自由に選べて, dp[i+1][true]の場合しか起こり得ない
- i桁目まででNと等しいと確定したdp[i][false]の場合, 次の2つが起こりえます.
- dp[i+1][false]: 次の桁はNのi+1桁目と等しくする必要がある
- dp[i+1][true] : 次の桁はNのi+1桁目未満から自由に選べる
このように桁DPでは配るDPで書いたほうがやりやすいと思います.
探索アルゴリズム
深さ優先探索: Depth First Search, DFS
木やグラフ探索の際に, 行き止まりになるまで深く潜って探索していく方法です.
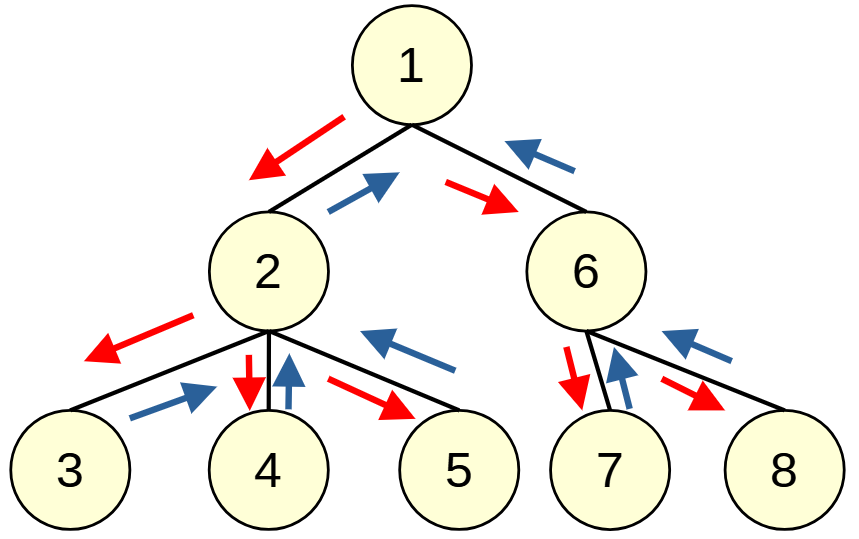
実装は, 再帰やstackで行えます.
void dfs_recursive(const vector< vector<int> > &adj, int s, vector<bool> &seen){
seen[s] = true; // sに訪問
for (auto to: adj[s])
if (!seen[to])// 未訪問頂点を辿る
dfs_recursive(adj, to, seen);
}
void dfs(const vector< vector<int> > &adj, int s, vector<bool> &seen){
stack<int> st;
st.push(s);
while (!st.empty()) {
int v = st.top();
st.pop();
seen[v] = true; // vに訪問
for (auto to: adj[v])
if (!seen[to]) // 未訪問頂点をスタックに積む
st.push(to);
}
}
- adj: グラフの隣接リスト
- adj[s]で頂点sから遷移できる頂点のリストが得られる
- seen[s]: sを訪問したかどうかのフラグ
- s: 訪問する頂点
DFSはグラフ上を走査したいときに再帰で簡単に書けるため, いろいろなアルゴリズムで使われます. (後述)
幅優先探索: Breadth First Search, BFS
木やグラフ探索の際に, 浅いところから探索していく方法です.
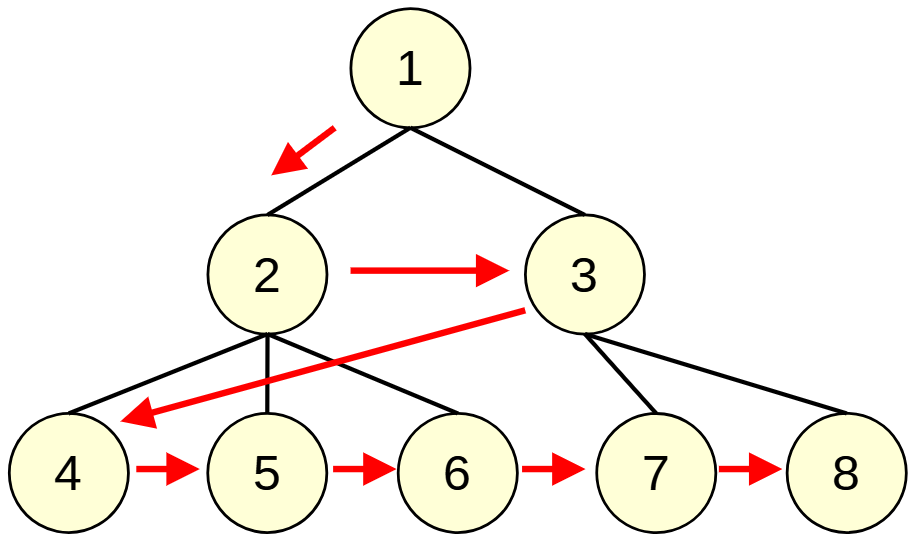
queueで実装できます.
void bfs(const vector< vector<int> > &adj, int s, vector<bool> &seen){
queue<int> que;
que.push(s);
while (!que.empty()){
int v = que.front();
que.pop();
seen[v] = true; // vに訪問
for (auto to : adj[v])
if (!seen[to])
que.push(to);
}
}
DFSのstackをqueueに変えただけです.
開始頂点sから最も近いところから探索していくことになるため, 辺の長さが全て等しければ, 最小の〇〇を見つけるという問題に使えます.
DFSからBFSにする際に, stackからqueueに変えたように, priority_queueに変えると, コストに応じた順に探索することができ, 最小値/最大値を求める系の問題でよく使います. (後述するダイクストラがその例)
全探索
スケールが小さい問題で, パターンをすべて列挙, 確認したりする際に使います.
単純にforループや再帰で書く他に, 次のようなテクニックがあります.
next_permutation
vector<int> v = {1,2,3};
do{
// あらゆるvのパターンがやってくる
} while(next_permutation(v.begin(),v.end()));
C++のnext_permutationを使うと, 辞書順に小さい方からあらゆるパターンを探索することができます.
この例では, 以下の3!=6通りループが回ります.
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
全探索するためには, 初期パターンを辞書順で最小のパターンから始める必要があります.
このようにnext_premutationを使うと再帰を自分で書くよりも楽できます.
また, 逆順に生成するprev_permutationもあります.
v={1,1,2}と重複ありで与えても, ちゃんと余分なパターンを生成することなく動きます.
1,1,2
1,2,1
2,1,1
bit全探索
整数のビット表現を使った探索です.
たとえば集合S={0,1,2,3}の部分集合を列挙するには, 各要素を選ぶか選ばないかで$2^4$パターンあります.
もちろん再帰でも書けますが, ビット表現を利用して, i番目のビットが0なら選ばない, 1なら選ぶと解釈して単純なforループで書くことができます.
int n = 4;
for (int i = 0; i < (1<<n); ++i){
// 0から2^n-1までの2^n通りのパターンがくる
for (int j = 0; j < n; ++j)
if (i&(1<<j)){
// jが選ばれた
}
}
二分探索
ソートされた配列に対して, 検索したい値が存在するか確認するアルゴリズムです.
C++では, binary_searchで行うことができますが, 存在確認だけをしたいことは少ないため, lower_boundやupper_boundをよく使います.
- lower_bound: 検索する値以上の値を持つ最初の位置のイテレータを返す
- upper_bound: 検索する値より大きい最初の位置のイテレータを返す
配列に関してはこれで十分ですが, 問題によっては自分で書く必要が出てきます.
例題: 競プロ典型90問 001 - Yokan Party(★4)
この問題では, 「答えがX以上で条件を満たすか?」を判定する関数を書き, 答えを二分探索することで解を求めます.
そのため, 自分でも書けるようにしておくことが大切です.
template<class T>
int bsearch(const vector<T> &vec, T key, bool lower_bound=true){
int left=0, right=vec.size()-1;
while(left <= right){
int mid = (left+right)/2;
T val = vec[mid]; // ここを任意の関数に書き換えてよく使う
if (val < key // 降順の場合は不等号を逆にする
|| (!lower_bound && val == key))
left=mid+1;
else
right=mid-1;
}
return left;
}
二分探索では, ソートされていることを利用して, だんだん探索範囲を絞っていきます.
真ん中の要素と比較することで, 探索範囲が半分ずつになっていくため, 計算量はO(log(n))です.
グラフ
頂点を辺で結んだ構造です. AtCoderでは頻出です.
ダイクストラ法: 単一始点最短経路問題
非負の重み付きグラフにおいて, 1頂点から他の頂点への最短距離を求めるアルゴリズムです.
priority_queueを使って, 各頂点への距離が現状で最短の距離となる頂点から訪問していくことで実装できます.
template<class T>
vector<T> dijkstra(const vector< vector< pair<int, T> > > &adj, int n, int s){ // (隣接, ノード数, 始点)
vector<T> dist(n, numeric_limits<T>::max()/2);
priority_queue< pair<T, int>, vector< pair<T, int> >, greater< pair<T, int> > > pq;
pq.push({0, s}); // (コスト, ノード)
dist[s] = 0;
vector<bool> seen(n, false);
while (!pq.empty()){
int v = pq.top().second;
pq.pop();
seen[v] = true;
for (auto [to, cost] : adj[v]){ // ノード v に隣接しているノードに対して
if (!seen[to] && dist[v] + cost < dist[to]){
dist[to] = dist[v] + cost;
pq.push({dist[to], to});
}
}
}
return dist;
}
基本構造は, DFSやBFSと変わらず, 代わりにpriority_queueを使っています.
各時点の暫定最短距離をdistに格納し, 確定したノードはseenをtrueとして訪問済みになります.
AtCoderのグラフ問題では頻出です.
例題: 競プロ典型90問 013 - Passing(★5)
01BFS
辺の重みが0か1である場合に, 各頂点に最小コストで訪問する探索手法です.
ダイクストラの重みを限定したバージョンなので, ダイクストラでも解けますが, プログラミング言語によってはダイクストラだとTLEになる場合があります.
priority_queueの代わりにdequeを使います.
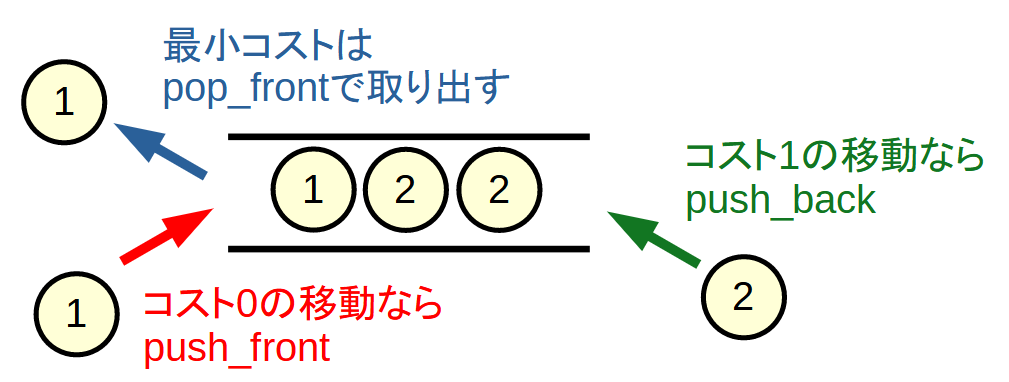
コストが01の2種類しかなく, 常に最小の値から探索するため, dequeに存在するコストの種類は高々2種類のみで, その差は高々1になります.
そのため, priority_queueを使うまでもなく, 以下のようにすることで, 常に最小値を取り出す構造ができます.
最小のコストをpop_frontした頂点から次の頂点へのコストが...
- 0の場合: push_frontする
- コストが変わらず最小であるため
- 1の場合: push_backする
- コストが1増えて最大となったため
迷路の問題でよく使われるイメージがあります.
例題: 競プロ典型90問 043 - Maze Challenge with Lack of Sleep(★4)
ワーシャルフロイド法: 全頂点ペアの最短経路
全頂点ペアの最短経路を求めるアルゴリズムです.
template<class T>
vector< vector<T> > floyd_warshall(const vector< vector<T> > &cost, int n) {// (移動コスト行列, 頂点数)
vector< vector<T> > cost_min = cost;
for(int i=0; i<n; ++i)
cost_min[i][i]=0;
for(int k=0; k<n;++k)for(int i=0;i<n;++i)for(int j=0;j<n;++j)
cost_min[i][j]=min(cost_min[i][j], cost_min[i][k]+cost_min[k][j]);
return cost_min;
}
3重forループを使って, 暫定コストを更新していきます.
頂点iから頂点jへの移動について, 頂点kを経由したときと比較して小さい方の値で更新していくアルゴリズムです.
計算量は頂点数の3乗です.
グラフのサイズが小さいときに使うことがあります.
強連結成分分解
有向グラフにおいて, お互いに行き来できる頂点のグループに分けることを強連結成分分解といいます.
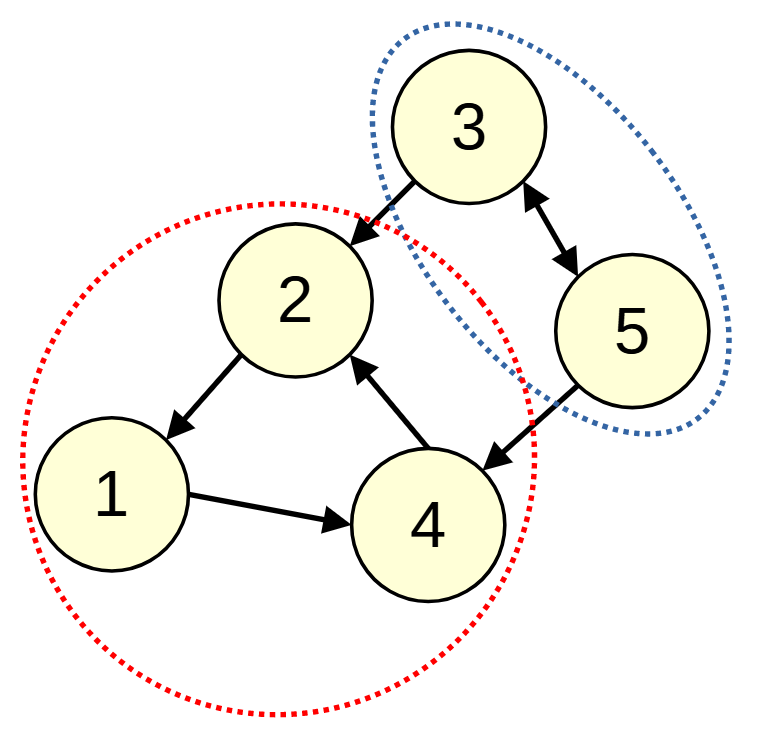
強連結成分分解のアルゴリズムは以下の通りです.
- 適当な頂点からDFSして去り際に頂点を記録する
- 有向グラフの向きを反転させたグラフを, 1.の訪問順の逆順を始点としてDFSする
- 2.で辿れた塊が1つの強連結成分である
証明などは別サイトに任せたいと思います.
実装すると以下のとおりです.
// 深さ優先で抜けるときにpushする
void _sccd(const vector< vector<int> > &adj, int s, vector<bool> &seen, vector<int> &visit){
seen[s] = true;
for(auto to : adj[s])
if (!seen[to])
_sccd(adj, to, seen, visit);
visit.push_back(s);
}
// Strongly Connected Component Decomposition (強連結成分分解)
vector< vector<int> > sccd(const vector< vector<int> > &adj, int n){
// 1. DFSで順序付け
vector<bool> seen(n, false);
vector<int> visit;
for(int s=0;s<n;++s)
if (!seen[s])
_sccd(adj, s, seen, visit);
// 2. 反転させたグラフをDFSの逆順でたどる
vector< vector<int> > adj_rev(n);
for(int i=0;i<n;++i)for(auto j : adj[i])
adj_rev[j].push_back(i);
seen = vector<bool>(n, false);
vector< vector<int> > connected;
for(auto it = visit.rbegin(); it != visit.rend(); ++it){
if (seen[*it])
continue;
vector<int> component;
_sccd(adj_rev, *it, seen, component);
connected.push_back(component);
}
return connected;
}
強連結成分分解を使う例題はこちら.
例題: 競プロ典型90問 021 - Come Back in One Piece(★5)
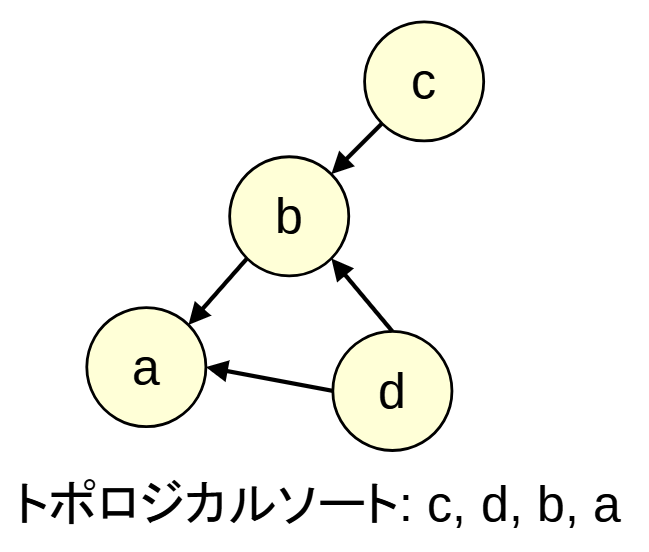
トポロジカルソート
有向グラフ上で, 頂点に順序をつけるアルゴリズムです.
どの頂点もその出力辺の先の頂点より前にくるように順序をつけます.
アルゴリズムは入次数がゼロの頂点を頂点番号の若い順にグラフから削除を繰り返すことで順序を付けれます.
vector<int> topological_sort(const vector< vector<int> > &adj, int n){
// 入次数
vector<int> indeg(n, 0);
for(int i=0;i<n;++i)for(auto j : adj[i])
indeg[j]++;
priority_queue< int, vector<int>, greater<int> > heap;
for(int i=0;i<n;++i)
if (indeg[i] == 0)
heap.push(i);
vector<int> ans;
while (!heap.empty()) {
// 入次数がゼロで番号が若い順に訪問する
int i = heap.top();
heap.pop();
ans.push_back(i);
// iをグラフから削除
for(auto j : adj[i]) {
indeg[j]--;
if (indeg[j] == 0)
heap.push(j);
}
}
return ans;
}
クラスカル法: 最小全域木
最小全域木は, 重み付き無向グラフで, 連結性を保ったまま, 辺のコストの和が最も小さくなるように辺を削除してできる木のことです.
アルゴリズムは以下の手順です.
- 辺が全く無い状態を考える
- コストの小さい順に辺を追加していく. ただし, 追加時に閉路ができてしまう場合は追加しない
template<class T>
T kruskal(vector< tuple<T,int,int> > edges, int n) {// edges: {cost, v1, v2}
// コストが小さい順にソート
sort(edges.begin(), edges.end());
UnionFind uf(n);
T min_cost = 0;
for(auto [cost, v1, v2] : edges) {
if (!uf.same(v1, v2)) {
// 辺を追加しても閉路ができないなら、その辺を採用する
min_cost += cost;
uf.merge(v1, v2);
}
}
return min_cost;
}
連結の判定には既に説明したUnionFindを使ってます.
数学
GCD(最大公約数)とLCM(最小公倍数)
最大公約数と最小公倍数には次の関係があります.
$$
a\times b = \mathrm{gcd}(a,b) * \mathrm{lcm}(a,b)
$$
覚えておくといいでしょう.
ちなみに, C++にはgcdとlcmの関数があります.
合同式: mod演算
整数$a,b$を$m$で割った余りが等しいとき$a \equiv b~(\mathrm{mod}~m)$と書きます.
AtCoderでは場合の数を計算する際に, オーバーフロー対策として$10^9+7$で割った余りを求める問題が多いです.
合同式の性質から, $a\equiv c$, $b\equiv d$のとき, 以下が成り立ちます.
- $a+b\equiv c+d$
- $ab\equiv cd$
- $a^n\equiv c^n$
和や積は同じ余りの整数で置き換えてよいということです.
競プロでは, 和や積の都度, %mで余りを取ればよいです.
注意が必要なのは次の割り算を含む場合です.
モジュラ逆数
$ax\equiv 1~(\mathrm{mod}~m)$を満たす$x$を$a$のモジュラ逆数といい, $a^{-1}$と書きます. (ただし, $a$と$m$は素. すなわち$\mathrm{gcd}(a,m)=1$)
例: $3\times 4\equiv 12\equiv 1~(\mathrm{mod}~11)$であるため, 3は4の逆数, 4は3の逆数です.
合同式では割り算に関して$\equiv$が成り立たないため, この逆数を使って計算することになります.
$n$個から$r$個とる組み合わせを計算する${}_nC_r$の実装例
template<class T>
T combi_mod(T n, T r, T mod){
T ans=1, div=1;
for (T i = n; i > n-r; --i)
ans = (ans*(i%mod))%mod;
for (T i = 1; i < r+1; ++i)
div = (div*(i%mod))%mod;
T inv_div = inverse(div, mod); // 整数の逆元
return (ans * inv_div) % mod;
}
${}_nC_r$の計算には割り算を含むため, 逆元の計算が必要になります.
inverse(div, mod)の実装は以下の通りです.
template<class T>
T inverse(T a, T prime_mod, bool euclid=true){
if (!euclid) // フェルマーの小定理
return pow_mod(a, prime_mod-2, prime_mod);
auto [x,y,g]=extend_euclid(a, prime_mod); // 拡張ユークリッド互除法
return ( (x<0) ? (x+prime_mod):x ) % prime_mod;
}
説明: 逆元の求め方には2パターンあります. (どちらかでよい)
- 拡張ユークリッド互除法
- 拡張ユークリッド互除法で$ax+my=\mathrm{gcd}(a,m)=1$の解$x,y$を求める
- 両辺をmod $m$で考えれば, $ax\equiv 1$であるため, 求めた$x$が$a^{-1}$である
- フェルマーの小定理 ($m$が素数であるという条件も必要)
- フェルマーの小定理から$a^{m-1}\equiv 1~(\mathrm{mod}~m)$である
- $a^{m-2}a\equiv 1$から$a^{m-2}$が$a^{-1}$である
AtCoderでは$m$は素数で与えられるため, フェルマーの小定理版も使うことができます.
ただし, $m$は非常に大きな整数であるため, $a^{m-2}$の計算には高速べき乗法を使います.
拡張ユークリッド互除法
gcdを求めるユークリッド互除法に少し計算を足したもので, $a,b$が与えられたときに, $ax+by=\mathrm{gcd}(a,b)$の解$x,y$と$\mathrm{gcd}(a,b)$を同時に求めることができます.
// 拡張ユークリッド互除法 ax + by = gcd(a,b) -> {x, y, gcd}
template<class T>
tuple<T,T,T> extend_euclid(T a, T b) {
T x0 = 1, x1 = 0, x2, y0 = 0, y1 = 1, y2, r0 = a, r1 = b, r2, q2;
while (r1 != 0) {
q2 = r0 / r1;
r2 = r0 % r1;
x2 = x0 - q2 * x1;
y2 = y0 - q2 * y1;
x0 = x1;
x1 = x2;
y0 = y1;
y1 = y2;
r0 = r1;
r1 = r2;
}
return {x0, y0, r0};
}
詳しい説明は他の方に任せようと思います.
高速べき乗法
$a^n$を高速に計算する方法です.
$n$のビット表現(2のべき)で考えることで, 高速化を実現します.
たとえば, $a^{100}$の場合,
$$
a^{100}=a^{64 + 32 + 4}=a^{2^6}a^{2^5}a^{2^2}
$$
というように$a^{2^k}$の形の積で書くことができます.
$$
a^{2^{(k+1)}}=(a^{2^k})^2
$$
であることに注意すると, 次のように実装できます.
template<class T>
T pow_mod(T a, T n, T mod){
T ans = 1;
a %= mod;
while (n > 0) {
if ((n & 1))
ans = (ans * a) % mod;
a = (a * a) % mod;
n >>= 1;
}
return ans;
}
オーバーフロー対策としてmodを取ってます.
素数
知識: $n$が素数であるかどうかは, $\sqrt{n}$以下の素数で割り切れるかできます.
素因数分解
素数の積に分解することです.
$n$を素数の積に分解するには, $\sqrt{n}$までの整数で割れるかを確認して行けばよいです.
次のように実装できます.
template<class T>
vector<T> pfact(T n){
vector<T> ans;
for (T i=2; i*i<=n; ++i){
while(n%i==0){
n/=i;
ans.push_back(i);
}
}
if (n!=1)
ans.push_back(n);
return ans;
}
例題: 競プロ典型90問 075 - Magic For Balls(★3)
エラトステネスのふるい: n以下の素数列挙
$n$以下の素数を列挙するアルゴリズムです.
- 素数かどうかを表す配列
is_primeを用意(初期値はALL true) - 2から$\sqrt{n}$までの整数iについて
-
is_prime[i]がfalseなら素数でないためスキップ -
is_prime[i]がtrueなら素数であるが, その倍数は素数ではないため配列に記録しておく-
is_prime[2i]=is_prime[3i]=...=falseとする
-
-
- 2から$n$以下の整数iのうち
is_prime[i]=trueであるものが$n$以下の素数
template<class T>
vector<T> eratosthenes(T n){
vector<T> ans;
vector<bool> is_prime(n+1, true);
for (T i=2; i*i<=n; ++i){
if(!is_prime[i]) continue;
for(T j=2*i; j<=n; j+=i)
is_prime[j] = false;
}
for (T i=2; i<=n; ++i)
if (is_prime[i]) ans.push_back(i);
return ans;
}
進数変換
B進数→10進数
B進数の整数が$a_n...a_2a_1a_0$と書かれているとき, 10進数で表すと,
$$
\sum_{i=0}^n a_iB^i
$$
です.
template<class T>
T to_base10(const string &x, int b){
T ans=0, base=1;
for(int i=x.length()-1; i>=0; --i){
int num = ('0'<=x[i]&&x[i]<='9') ? (x[i]-'0') : (x[i]-'A'+10);
ans+=base*num;
base*=b;
}
return ans;
}
10進数→B進数
逆に, 10進数をB進数に直すには, Bで割った余りを考えればよいです.
template<class T>
string to_baseB(T x, int b){
string ans;
do{
int num = x%b;
ans = (char)( (num<=9) ? ('0'+num) : ('A'+num-10) ) + ans;
x/=b;
}while(x!=0);
return ans;
}
その他
いもす法
いもす法は, 開始地点と終点のみに記録したあと, あとから累積和をとることで所望の結果を得る方法です.
以下は長方形領域を塗りつぶす手順です.
例題: 競プロ典型90問 028 - Cluttered Paper(★4)
この例題は, たくさんの長方形が与えられ, 重なった枚数ごとの面積を求める問題です.
長方形の4つの角に記録しておいて, 最後に1回だけ累積和を横方向,縦方向で取ることで, マスごとに重なっている長方形の数が求められます.
LIS: 最長増加部分列の長さ
与えられた数列$A=a_1, ..., a_n$の増加部分列$B=a_{i_1},...,a_{i_n}$の最大長を求める問題です. ただし, $i_1<\cdots <i_n$かつ$a_{i_1}<\cdots <a_{i_n}$.
こちらの方の記事がわかりやすいです.
私の実装を置いておきます.
template<class T>
size_t LIS(const vector<T> &ary){
vector<T> dp;// 長さkである増加部分列のうち, 最後の要素の最小値
dp.reserve(ary.size());
for(T a : ary){
auto it=lower_bound(dp.begin(), dp.end(), a);
if (it!=dp.end())
*it=a;
else
dp.push_back(a);
}
return dp.size();
}
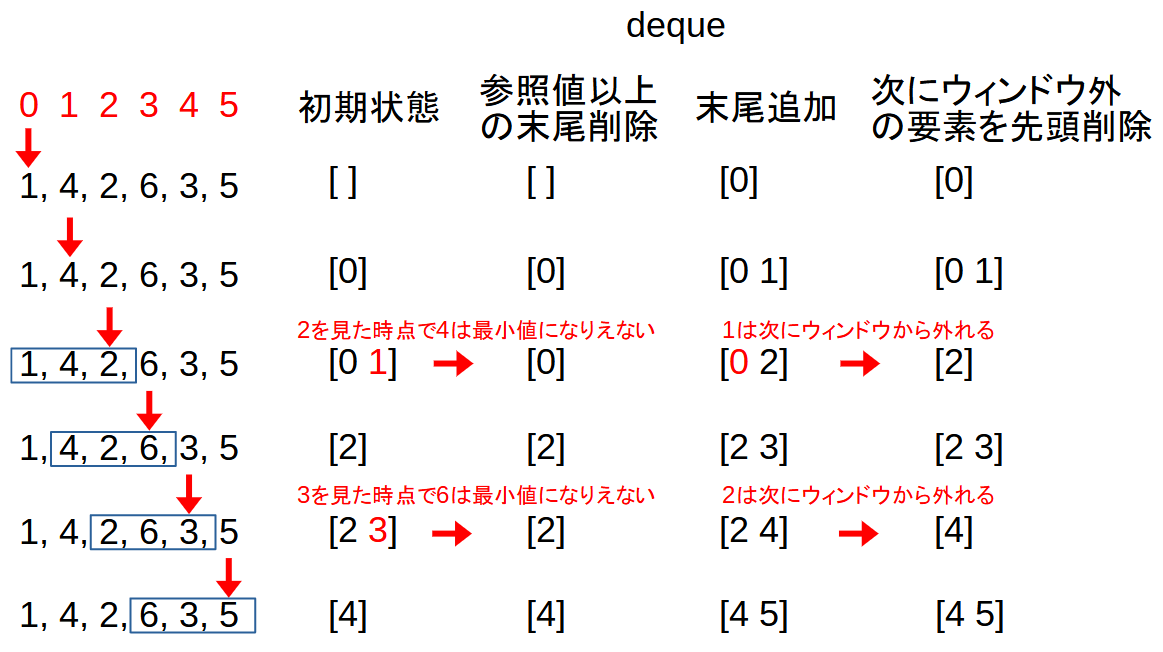
スライド最小値
数列$A_0,\ldots, A_{n-1}$に対して, 長さ$k$のウィンドウの最小値を格納した数列$B_i=\min\{A_i,...,A_{i+k-1}\} ~(0\le i\le n-k)$を求める問題です.
dequeを使って, O(n)で求めることができます.
- dequeで配列のindexを管理します
- deque内のindexは, 先頭から末尾まで, Aに関して単調増加になるようにします
A[deque.front()]<...<A[deque.back()]
- 現在参照している
A[i]の値以上の値を参照するdequeの要素を末尾から削除していくことで, この先参照する最小値のみのindexを格納できます - ウィンドウサイズkからはみ出たindexはdequeの先頭から削除します
template<class T>
vector<T> slide_min(const vector<T> &ary, int k){
vector<T> ans(ary.size()-k+1);
deque<int> q;
for(int i=0;i<ary.sise();++i){
// 現在の値以上を持つ場合削除
while(!q.empty() && ary[q.back()] >= ary[i])
q.pop_back();
q.push_back(i);
if (i-k+1 >= 0) {
ans[i-k+1] = ary[q.front()];
// ウィンドウから外れるため削除
if (q.front() == i-k+1)
q.pop_front();
}
}
return ans;
}
例題: 競プロ典型90問 060 - Chimera(★5)
その他の知識
- 差の二乗が最小となる点は平均値
- 差の絶対値が最小となる点は中央値
など、知っていると簡単に解ける問題もあります。
既にまとめている方がいるのでリンクを貼っておきます.
競技プログラミングで解法を思いつくための典型的な考え方
C++の楽な記法とABC用テンプレート
もともと便利なマクロや, C++11, C++17と進んで行きだんだん楽な記法が増えてきたので紹介します.
for
イテレータやインデックスを使って回さずとも, forとコロンで楽に書くことができます.
vector<int> v{1,2,3,4,5};
for (auto e : v)
cout<<e<<endl;
参照渡しさせる場合は, auto &e : vのように&をつければよいです.
tuple, pair, map
タプルやペアの作成や分解を楽に書くことができます.
tuple<int, double> t = {1, 2.0}; // タプル作成
auto &[i, d] = t; // 分解
map<int, int> m{{1,2},{3,4}};
for (auto &[k,v]: m)// keyとvalueを参照しながらループ
cout<<k<<":"<<v<<endl;
vector< pair<int,int> > vp;
vp.push_back({2,1}); // 楽にペアを追加
関数の戻り値でreturn {1, 0}のように書くこともできます.
c++11まで必要だったmake_tupleもc++17では不要です.
マクロ定義
#define FOR(i, a, b) for(int i = (a); i < (b); ++i)
#define REP(i, n) FOR(i, 0, n)
競プロではループを何度も書きます.
ループを書く際に, 毎回for(int i = 0; i < n; ++i)を書くのは面倒です.
上記のようなマクロを定義しておくことで, REP(i, n)のように書くことができます.
これは単純に書く量を減らすことができるだけではなく, 変数名を変える際のミスを防ぐことにも繋がります. たとえば, iをjに変える場合, for(int i = 0; i < n; ++i)だと3箇所のiをjに変えなければいけませんが, REP(i, n)なら1箇所で済みます.
その他, よく使うものをテンプレートに含めました.
型のエイリアス定義
using LL = long long;
using VI = vector<int>;
using VVI = vector<VI>;
vector<int>やvector< vector<int> >をよく使いますが, 毎回書いていると長いため, VIやVVIで書けるようにしてます.
その他, よく使うものを定義してます.
オペレーター定義
template<class T> ostream& operator<<(ostream& os, const vector<T>& vec) {
os << "[ ";
for ( const T& item : vec )
os << item << ", ";
os << "]"; return os;
}
template<class T> istream& operator>>(istream& is, vector<T>& vec) {
for ( T& item : vec )
is >> item;
return is;
}
vectorを表示させるには通常ループさせるしかありませんが, operatorを定義しておくことで毎回書かなくて済むようになります.
たとえば, 次のような書き方が可能になります.
VI vec(3);
cin >> vec;
cout << vec;
10 20 30 (入力)
[ 10, 20, 30, ]
もちろん再帰的に実行されるため, 2次元配列の入力でも楽できます.
VVI mat(3, VI(4));
cin >> mat;
出力は主にデバッグ時によく使ってます.
その他, pairやtuple, set, mapにオペレーターを定義してます.
その他
template <class Head> void OUT(Head&& head) {
cout << head << endl;
}
template <class Head, class... Tail> void OUT(Head&& head, Tail&&... tail) {
cout << head << " ";
OUT(forward<Tail>(tail)...);
}
template <class Head> void IN(Head&& head) {
cin >> head;
}
template <class Head, class... Tail> void IN(Head&& head, Tail&&... tail) {
cin >> head;
IN(forward<Tail>(tail)...);
}
地味に定義して楽だったのが, スペース区切りの出力を行う関数の定義です.
AtCoderではスペース区切りで出力することが多く, cout<<a<<" "<<b<<" "<<c<<endl;と書くのが面倒なため, それを楽にする関数を定義しました.
int a,b,c;
IN(a,b,c);
OUT(a,b,c);
1 2 3 (入力)
1 2 3
あとがき
ABCは, 長々とガリガリコードを書くというよりは, ちゃんとアルゴリズムを思いつけるかが重要だと感じました. なので, 楽な書き方ができたからといって, 直接順位の向上につながるわけではありませんが, 自分なりの使いやすい環境を用意しておくことは, ストレスを少なくやっていく上で重要だと思ってます.
今回C++で紹介しましたが, pythonでも十分やることができます. 実際にpythonで強い方もいます. 最初はpythonでやっていた私がC++に移行した理由は, オーダーが同じでも定数倍の差でpythonだと通らないことを経験したり, やっている最中に「これC++なら通るだろうな」「pythonなら書き方工夫しなきゃ通らないな」と思うことがあったからです. (それと, もともとプログラミング自体Cから始めた人だからというのも大きいです) C++は良くも悪くもカスタマイズ性の高い言語なので, 今回紹介したようにpythonくらい記述が楽になれば, python使う意味もないなぁと思いました.
この記事を読んで「面白かった」「学びがあった」と思っていただけた方, よろしければTwitterやFacebook, はてなブックマークにてコメントをお願いします!
また DeNA 公式 Twitter アカウント @DeNAxTech では, Blog記事だけでなく様々な登壇の資料や動画も発信してます. ぜひフォローして下さい!
Follow @DeNAxTech
DeNAでは今年, 2021年度新卒エンジニア・2022年度新卒内定エンジニアの Advent Calendar もあります!
本 Advent Calendar とは違った種類, 違った視点での記事をぜひお楽しみください!
▼DeNA 2021年度新卒エンジニア・2022年度新卒内定エンジニアによる Advent Calendar 2021
https://qiita.com/advent-calendar/2021/dena-21x22