今回は、何も知らないところからバンディットアルゴリズムを学びました。
シンプルなバンディットアルゴリズムから、各ユーザーごとに最適化するContextual Bandit、順序を最適化するCascading Banditまで解説します。
学んでいて疑問に思ったことを解消しつつ記載しています。
ソースコード
https://github.com/birdwatcherYT/bandit
対象読者
- バンディットアルゴリズムを理解して実装したい人
- ユーザーごとにカスタマイズしたバンディットを理解して実装したい人(Contextual Bandit)
- 順序を最適化するバンディットを使いたい人(Cascading Bandit)
バンディットアルゴリズム
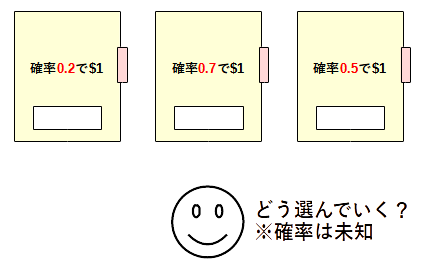
- スロットマシンN台がある
- スロットマシンの腕を引くと報酬がもらえる
- 累積報酬を最大化したい
バンディットアルゴリズムは累積報酬を最大化するための戦略を示してくれます。
報酬は、0/1報酬だったり、連続報酬だったりします。
たとえば、クリックしたかどうかは0/1報酬で、どれだけの時間動画を見たかは連続報酬です。
応用例
- ABテストの代わりに使って自動的に優秀なシステムが残る
- たとえば、広告配置アルゴリズムA,B,Cのどれが優れているかを調べる際に、各アルゴリズムをバンディットの腕として、報酬をクリックしたかどうかとすると、最もクリック率の高いアルゴリズムが自動的に残ることになります
- 企業の活用事例
-
ZOZOTOWNにおけるバンディットアルゴリズムを用いた推薦
- ユーザーベクトルに応じてアイテムを推薦
-
Artwork Personalization at Netflix
- サムネをユーザーベクトルに応じて最適化
-
ZOZOTOWNにおけるバンディットアルゴリズムを用いた推薦
アルゴリズム
何も知識の無い状態から腕を引いていき、知見を貯めながら、良さそうな腕を見極めていきます。
これまでの知識を「活用」したり、もっと良い腕があるかもしれないと別の腕を「探索」しながら累積報酬を最大化していきます。
主なアルゴリズムをいくつか紹介します。
Epsilon Greedy
- (活用) $1-\varepsilon$の確率で、これまでの平均報酬が最も良い腕を選択
- (探索) $\varepsilon$の確率で、ランダムな腕を選択
経験的に一番良い腕を引いていくが、小さい確率で別の腕も選ぶという非常にシンプルなアルゴリズムです。
UCB1(Upper Confidence Bound)
選ぶ腕 = \arg\max_a \Biggl(\underbrace
{腕aの報酬の平均値}_{活用} + \underbrace{\sqrt{\frac{2\log(全体の試行回数)}{腕aの試行回数}}}_{探索}\Biggr)
確率不等式を使って導出された理論に基づくアルゴリズムです。
第1項ではこれまでの試行から最も良さそうな腕を、第2項では試行回数が少なく評価が不確かな腕ほど選ぶような基準になってます。
FAQ
- 報酬が0/1じゃないときでもこのまま使える?
- No
- UCB1の導出過程で、報酬が[0,1]の範囲であることを仮定しているため、そのまま使うとパフォーマンスが悪い可能性があります
- 探索と活用のバランス調整のため、係数調整が必要になります
- おそらく、0/1の場合でも係数調整したほうがいいです
- UCB1の1って何?
- UCB1というアルゴリズムの名前で、改良版のUCB2やUCB1-Tunedなどもあります
- Upper Confidence Boundって何?
- 信頼区間の上限のことで、「真の期待値を過小評価している確率」の上限を抑えることを考えて導出されてます
理論をもう少し詳しく知りたい方へ
【ヘフディングの不等式】 $[a_i,b_i]$の範囲をとる独立な$n$個の確率変数$X_i$の平均を$\bar{X}$、期待値を$E[\bar{X}]$としたとき、任意の$u>0$に対して $$ P \left[\bar{X}-E\left[\bar{X}\right] \geq u\right] \leq \exp\left(-\frac{2n^2u^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\right) $$ が成り立つ。ヘフディングの不等式において、$X_i$を$-X_i$として適用すれば、
$$
P \left[E\left[\bar{X}\right]-\bar{X} \geq u\right] \leq \exp\left(-\frac{2n^2u^2}{\sum_{i=1}^{n}(b_i-a_i)^2}\right)
$$
も成り立ちます。
この不等式を使って、試行回数が増えるごとに$E[\bar{X}]-\bar{X}$を抑えるように決めた$u$の値が第2項として現れているのです。
参考文献
Thompson Sampling
確率的に腕を選択する優れたアルゴリズムで、以下のような流れになってます。
- 報酬の分布$p(r|\theta_a)$と、その未知パラメータ$\theta_a$の事前分布$p(\theta_a)$を仮定し、得られた知識$D_a$を用いてベイズの定理でパラメータの事後分布を計算:
\underbrace{p(\theta_a | D_a)}_{事後分布} = \frac{p(\theta_a)p(D_a | \theta_a)}{p(D_a)}
\propto \underbrace{p(\theta_a)}_{事前分布}\underbrace{p(D_a | \theta_a) }_{尤度}
= p(\theta_a)\prod_{r\in D_a} p(r | \theta_a)
- $選ぶ腕 = \arg\max_a y_a$
- $y_a \sim p(\theta_a|D_a)$: パラメータの事後分布からサンプリング
たとえば、報酬の分布として以下のようなものを扱います。
- ベルヌーイ分布(0/1報酬)
- 未知パラメータ:報酬1を返す確率
- 正規分布(連続報酬)
- 未知パラメータ:報酬の平均値(と分散)
TSではこれらの未知パラメータを推定しているわけです。
具体例を見たほうがわかりやすいと思うので、これらの分布を詳しく見ていきます。
ベルヌーイ分布(0/1報酬)
まずは、 報酬の分布 がベルヌーイ分布の場合です。
ベルヌーイ分布は、確率$\theta_a$で報酬1、確率$1-\theta_a$で報酬0という分布で、
$$\mathrm{Ber}(r|\theta_a)=\theta_a^r(1-\theta_a)^{1-r}, ~(r=0,1)$$
と表現されます。
まさに問題設定で説明した状況ですね。
この$\theta_a$が最も大きい腕$a$を選んでいきたいが、$\theta_a$が未知なので得られた知識をもとに推定しなければいけません。
そのために、未知パラメータ$\theta_a$の事前分布を設定します。
ベルヌーイ分布の共役事前分布はベータ分布なので、ベータ分布を $\theta_a$の事前分布 とします。
ベータ分布は
$$
\mathrm{Beta}(\theta_a|\alpha, \beta)=\frac{\theta_a^{\alpha-1}(1-\theta_a)^{\beta-1}}{B(\alpha, \beta)}
$$
です。
$B(\alpha,\beta)$はベータ関数で、積分したときに確率を1にするための正規化係数です。
ベータ分布は次のような形をしています。
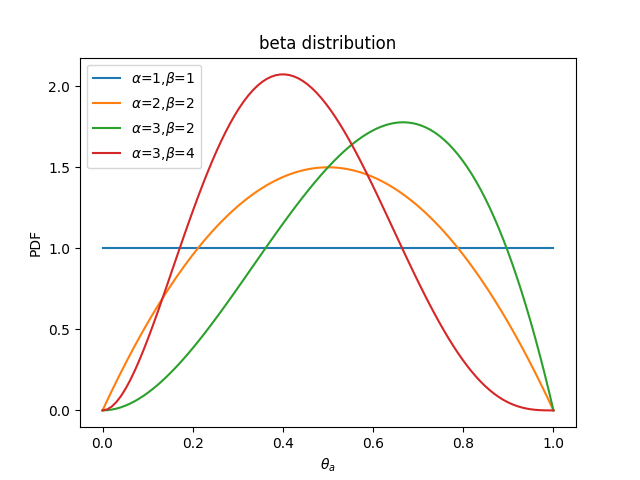
$\theta_a$についてなんの知識もなければ、$\alpha=\beta=1$を使うことになります。
以上で準備が整ったので、腕$a$を引いて得られた報酬の結果$D_a$を用いて、事後分布を計算します。
\begin{align*}
p(\theta_a)\prod_{r\in D_a} p(r | \theta_a)&=\mathrm{Beta}(\theta_a|\alpha, \beta)\prod_{r\in D_a}\mathrm{Ber}(r|\theta_a) \\
&\propto \theta_a^{\alpha-1+n_{a,1}}(1-\theta_a)^{\beta-1+n_{a,0}}\\
&\propto\mathrm{Beta}(\theta_a|\alpha+n_{a,1}, \beta+n_{a,0})
\end{align*}
- $n_{a,1}: 腕aを引いて報酬が1だった数$
- $n_{a,0}: 腕aを引いて報酬が0だった数$
すなわち、$\mathrm{Beta}(\theta_a|\alpha+n_1, \beta+n_0)$からサンプリングした値が最大の腕を選べばよいことになります。
実装上は、個数を覚えておくだけでいいので楽ですね。
アルゴリズム
- $\alpha_a\leftarrow 1,~ \beta_a\leftarrow1, \forall a$
- ループ
- $y_a\sim\mathrm{Beta}(\theta_a|\alpha_a, \beta_a), \forall a$
- $\tilde{a}=\arg\max_a y_a$
- 腕$\tilde{a}$を選んだ結果、報酬$r$を受け取る
- $\alpha_{\tilde{a}}\leftarrow\alpha_{\tilde{a}}+r, ~\beta_{\tilde{a}}\leftarrow\beta_{\tilde{a}}+(1-r)$
正規分布(連続報酬)
同様の手順で、報酬が正規分布に従う場合も見てみます。
(これ以降、腕$a$の添え字を省略します)
平均$\mu$、分散$\sigma^2$の正規分布に従った報酬がもらえる設定です。
$$
\mathrm{Norm}(r|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(r-\mu)^2}{2\sigma^2}\right\}
$$
パラメータが$\mu,\sigma$の2つあり、$\mu$が最大の腕を選びたいので当然$\mu$は未知ですが、$\sigma$が未知かどうかで事前分布が変わってきます。
共役事前分布:
- 正規分布(平均未知、分散既知)
- ガウスガンマ分布(平均未知、分散未知)
ここでは$\mu,\sigma$の両方未知として事後分布を計算してみよう。
これ以降、分散$\sigma^2$は精度$\lambda=1/\sigma^2$として登場します。
ガウスガンマ分布は、正規分布とガンマ分布の積で表される分布です。
$$
\mathrm{NG}(\mu, \lambda | m, \beta, a, b) = \mathrm{Norm}(\mu | m, (\beta \lambda)^{-1})\mathrm{Gam}(\lambda | a, b)
$$
- $\mathrm{Norm}(\mu | m, (\beta \lambda)^{-1})=(\frac{\beta \lambda}{2 \pi})^{1/2}\exp \{- \frac{\beta \lambda}{2}(\mu - m)^2\}$
- $\mathrm{Gam}(\lambda | a, b)=\frac{b^a}{\Gamma(a)}\lambda^{a-1} \exp(- b \lambda)$
パラメータの事後分布を計算します。
\begin{align*}
p(\mu,\lambda)\prod_r p(r | \mu,\lambda)
&=\mathrm{NG}(\mu,\lambda|m,\beta,a,b)\prod_r \mathrm{Norm}(r|\mu,1/\lambda)\\
&= \mathrm{Norm}(\mu | m, (\beta \lambda)^{-1})\mathrm{Gam}(\lambda | a, b)
(\frac{\lambda}{2\pi})^{n/2}\exp\{-\frac{\lambda}{2}\sum_r(r-\mu)^2\}\\
&\propto \lambda^{1/2}\lambda^{a+n/2-1}
\exp\left\{
-\frac{\lambda}{2}(\beta+n)\left(\mu-\frac{(\beta m+\sum_r r)}{(n+\beta)}\right)^2
-\lambda\left[
b+\frac{1}{2}\{\sum_rr^2+\beta m^2 -\frac{(\beta m+\sum_r r)^2}{\beta+n}\}\right]
\right\}\\
&\propto \mathrm{NG}\left(\mu,\lambda\Bigg|\frac{m\beta+\sum_rr}{\beta+n},\beta+n,a+n/2,b+\frac{1}{2}\{\sum_rr^2+\beta m^2 -\frac{(\beta m+\sum_r r)^2}{\beta+n}\}\right)
\end{align*}
exp内の平方完成
\begin{align*}
&-\frac{\lambda}{2}\sum(r-\mu)^2- \frac{\beta \lambda}{2}(\mu - m)^2-b\lambda\\
&= -\frac{\lambda}{2}[\sum r^2-2\mu\sum r+\mu^2n+\beta\mu^2-2\beta \mu m + \beta m^2]-b\lambda\\
&= -\frac{\lambda}{2}[(n+\beta)\mu^2-2(\beta m+\sum r)\mu+\sum r^2+\beta m^2]-b\lambda\\
&= -\frac{\lambda(n+\beta)}{2}[\mu^2-2\frac{(\beta m+\sum r)}{(n+\beta)}\mu+\frac{\sum r^2+\beta m^2}{(n+\beta)}]-b\lambda\\
&= -\frac{\lambda(n+\beta)}{2}[(\mu-\frac{(\beta m+\sum r)}{(n+\beta)})^2-\frac{(\beta m+\sum r)^2}{(n+\beta)^2}+\frac{\sum r^2+\beta m^2}{(n+\beta)}]-b\lambda\\
&=
-\frac{\lambda}{2}(\beta+n)\left(\mu-\frac{(\beta m+\sum r)}{(n+\beta)}\right)^2
-\lambda\left[
b+\frac{1}{2}\{\sum r^2+\beta m^2 -\frac{(\beta m+\sum r)^2}{\beta+n}\}\right]
\end{align*}
求めたNG分布からサンプリングすることになりますが、依存関係が$\lambda\to\mu$の順なので、この順にサンプリングし、最大の$\mu$を生成した腕を選択すればよいです。
アルゴリズム(文字が被るため腕の添字を$s$にしています)
- $a_s\leftarrow 1,b_s\leftarrow 1, m_s\leftarrow 0, \beta_s\leftarrow 1, \forall s$
- ループ
- $\tilde{\lambda}_s\sim\mathrm{Gam}(\lambda_s | a_s, b_s) , \forall s$
- $\tilde{\mu}_s\sim\mathrm{Norm}(\mu_s | m_s, (\beta_s \tilde{\lambda}_s)^{-1}) , \forall s$
- $\tilde{a}=\arg\max_s \tilde{\mu}_s$
- 腕$\tilde{a}$を選んだ結果、報酬$r$を受け取る
- $a_{\tilde{a}}\leftarrow a_{\tilde{a}}+1/2,b_{\tilde{a}}\leftarrow b_{\tilde{a}}+\frac{1}{2}\frac{\beta_{\tilde{a}}(m_{\tilde{a}}- r)^2}{\beta_{\tilde{a}}+1}, m_{\tilde{a}}\leftarrow\frac{m_{\tilde{a}}\beta_{\tilde{a}}+r}{\beta_{\tilde{a}}+1},\beta_{\tilde{a}}\leftarrow\beta_{\tilde{a}}+1$
実験
バンディットの比較実験では、リグレットがよく使われます。
リグレット(後悔)とは、真のパラメータを知っている神目線で常にベストな手を選んだ場合との差の期待値です。
試行$T$回目までの累積リグレットは次のように定義されます。
$$
\mathrm{regret}(T)=E[\max_a \sum_{t=1}^T(X_{a,t} - X_{\tilde{a}_t,t})]
$$
実際に真のパラメータを設定して学習させてみました。
0/1報酬の場合
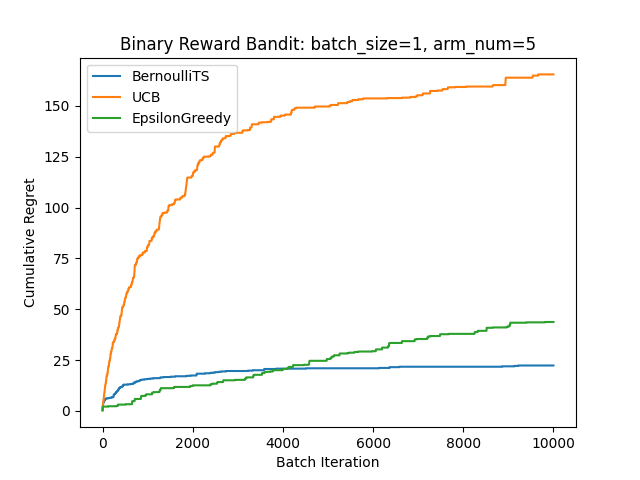
連続報酬の場合
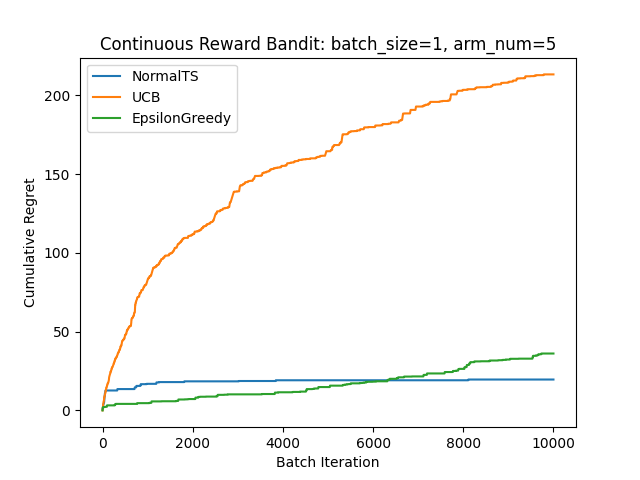
どちらもTSが強いですね。
参考文献
-
Bandit Algorithms in Information Retrieval
- バンディットのサーベイ論文
Contextual Bandit
通常のバンディットで全ユーザーが腕を引く場合、全体的に最適な腕を残すようにアルゴリズムが動きますが、ユーザーごとに好みが異なる場合があります。
ユーザー1人1人にバンディットのパラメータを持たせることもできますが、ユーザー1人だけで収束させるだけの試行回数を稼ぐことは現実的ではありません。(ユーザーをクラスタリングしてクラスタごとに通常のバンディットを適用させる策もあります。)
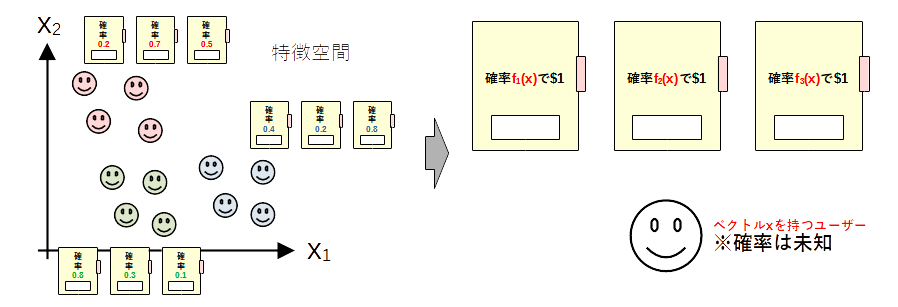
そこで登場するのがContextual Banditです。
- ユーザー特徴ベクトル$x$(context)を考慮したBanditです
- たとえば、ユーザーの性別、年齢、行動履歴などからベクトルを作ります
- $f_a(x)$に依存した報酬が得られるというモデルです
アルゴリズム
今回は$x^\top\theta_a$に依存した線形モデルを4つ紹介します。
アルゴリズムでは、パラメータ$\theta_a$を学習するわけです。
(もちろん$f_a(x)$にニューラルネットワークを用いたものもあります。)
- 報酬が$f_a(x)=x^\top\theta_a+\epsilon$で表現されると仮定
- LinUCB
- LinTS
- 確率$f_a(x)=\mathrm{sigmoid}(x^\top\theta_a)$で報酬1を、確率$1-f_a(x)$で報酬0を仮定
- LogisticTS
- LogisticPGTS
LinUCB
報酬が$r=x^\top \theta_a^*+\epsilon$に依存して得られることを仮定します。(誤差は$E[\epsilon]=0$を満たすものとします)
観測データ$D_a=\{(x_{a,t}, r_{a,t})\}_{t=1}^{t=T_a}$が得られているとき、リッジ回帰をすると推定値
\hat{\theta}_a=(X_a^\top X_a+\lambda I)^{-1}X_a^\top \Gamma_a
=\underbrace{(\sum_t x_{a,t} x_{a,t}^\top+\lambda I)}_{=:A_a}{}^{-1}\underbrace{(\sum_t r_{a,t} x_{a,t})}_{=: b_a}
=A_a^{-1}b_a
を得ます。
- $X_a=[x_{a,1},\ldots,x_{a,T_a}]^\top$
- $\Gamma_a=[r_{a,1},\ldots, r_{a,T_a}]^\top$
確率不等式でUCBを求めることで以下の選択基準を得ます。
$$
選ぶ腕 = \arg\max_a \left( x^\top \hat{\theta}_a+\alpha \sqrt{x^\top A_a^{-1}x} \right)
$$
- $\alpha>0$: 探索の度合い(ハイパーパラメータ)
確率不等式
少なくとも$1-\delta$の確率で
|x^\top\hat\theta_a-x^\top\theta_a^*|\le \underbrace{1+\sqrt{\log(2/\delta)/2}}_{=:\alpha} \sqrt{x^\top A_a^{-1} x}
が成り立つ。
真の値との差を押さえているわけです。
アルゴリズム
- $A_a\leftarrow \lambda I, b_a\leftarrow 0, \forall a$
- ループ(特徴ベクトル$x$を受け取る)
- $\tilde{a}=\arg\max_a ( x^\top \hat{\theta}_a+\alpha \sqrt{x^\top A_a^{-1}x} )$
- 腕$\tilde{a}$を提示して報酬$r$を受け取る
- $A_{\tilde{a}}\leftarrow A_{\tilde{a}}+xx^\top, b_{\tilde{a}}\leftarrow b_{\tilde{a}}+ rx$
毎回$A^{-1}$を求める必要がありますが、ランク1行列による修正しか行われないためSherman–Morrisonの公式を使って、計算量を削減できます。
$$
(A+xx^\top)^{-1}= A^{-1}-\frac{A^{-1}x x^\top A^{-1}}{x^\top A^{-1}x+1}
$$
参考文献
LinTS
LinUCBのトンプソンサンプリング(TS)バージョンです。
報酬が$r=x^\top \theta_a^*+\epsilon$で得られ、誤差が$\epsilon \sim \mathrm{Norm}(0, \sigma^2)$に従うことを仮定します。(簡単のため$\sigma$は既知とします)
このとき、報酬は$r \sim \mathrm{Norm}(\theta_a^{\top}x, \sigma^2)$に従います。
パラメータ$\theta_a$の事前分布を$\theta_a \sim \mathrm{MultiNorm}(\theta|0, \sigma_0^2I)$として、事後分布を計算します。
\begin{align*}
p (\theta_a | D_a ) &\propto p (\theta_a) \prod_{(x,r)\in D_a} p(r | \theta_a) \\
&\propto \exp \Bigl(-\frac{\theta_a^{\top} \theta_a}{2\sigma_0^2} \Bigr) \exp \Bigl(-\frac{1}{2\sigma^2}\sum_{(x,r)\in D_a} (r - \theta_a^{\top} x )^2 \Bigr) \\
& \propto \exp \Biggl(-\frac{1}{2\sigma^2} \Bigl(\theta_a^{\top} \underbrace{\bigl(\frac{\sigma^2}{\sigma_0^2}I + \sum_{(x,r)\in D_a} x x^{\top} \bigr)}_{=: A_{a}}\theta_a - 2 \theta_a^{\top}\underbrace{\sum_{(x,r)\in D_a} r x}_{=: b_{a}} \Bigr) \Biggr) \\
& \propto \exp \Bigl(-\frac{1}{2\sigma^2} (\theta_a - A_{a}^{-1}b_{a})^{\top} A_{a} (\theta_a - A_{a}^{-1}b_{a} ) \Bigr)\\
& \propto\mathrm{MultiNorm}(\theta_a|A_{a}^{-1}b_{a}, \sigma^2 A_{a}^{-1})
\end{align*}
アルゴリズム
- $A_a\leftarrow \frac{\sigma^2}{\sigma_0^2} I, b_a\leftarrow 0, \forall a$
- ループ(特徴ベクトル$x$を受け取る)
- $ \tilde\theta_a \sim \mathrm{MultiNorm}(\theta_a|A_{a}^{-1}b_{a}, \sigma^2 A_{a}^{-1}), \forall a $
- $\tilde{a}=\arg\max_a x^\top\tilde{\theta}_a$
- 腕$\tilde{a}$を提示して報酬$r$を受け取る
- $A_{\tilde{a}}\leftarrow A_{\tilde{a}}+xx^\top, b_{\tilde{a}}\leftarrow b_{\tilde{a}}+ rx$
参考文献
LogisticTS
0/1報酬の場合のトンプソンサンプリングです。
報酬のベルヌーイ分布をシグモイド関数$\mathrm{sigmoid}(z)=\frac{1}{1+\exp(-z)}$を使って、
$$
p(r|\theta_a)=\mathrm{sigmoid}(\underbrace{(2r-1)}_{=:y\in\{\pm1\}}x^\top \theta_a)
=\mathrm{sigmoid}(yx^\top \theta_a)
$$
と表現します。
sigmoid関数の性質
- $\mathrm{sigmoid}(-z)=1-\mathrm{sigmoid}(z)$
- $\mathrm{sigmoid}'(z)=\mathrm{sigmoid}(z)(1-\mathrm{sigmoid}(z))$
$\theta_a$の事前分布を$\mathrm{MultiNorm}(\theta_a|\mu_0, \Sigma_0)$として、事後分布の負の対数を計算します。
\begin{align*}
- \log p (\theta_a | D_a ) & = -\log p (\theta_a) -\sum_{(x,r)\in D_a}\log p(r | \theta_a ) +\mathrm{const.}\\
&= \frac{(\theta_a-\mu_0)^{\top} \Sigma_0^{-1}(\theta_a-\mu_0)}{2} - \sum_{(x,r)\in D_a} \log\mathrm{sigmoid}(y\theta_a^{\top} x) + \mathrm{const.}
\end{align*}
きれいな分布にならないので、勾配法(ニュートン法など)で最小値を与える$\hat{\theta}_a$を求めて、その周りで二次近似します。(最小値における微分値はゼロなため1次の項は0で消えてます)
$$
-\log p (\theta_a | D_a ) \approx \frac{1}{2} (\theta_a - \hat{\theta}_a)^{\top} H(\hat{\theta}_a) (\theta_a - \hat{\theta}_a ) + \mathrm{const.}
$$
ここで$H(\cdot)$はヘシアンです。
\begin{align*}
G(\theta_a)&:=-\nabla_{\theta_a} \log p (\theta_a | D_a ) = {\Sigma_0^{-1}(\theta_a-\mu_0) }- \sum_{(x,r)\in D_a} \mathrm{sigmoid}(-y\theta_a^{\top} x) y x\\
H(\theta_a)&:=- \nabla_{\theta_a}^2 \log p (\theta_a | D_a ) = {\Sigma_0^{-1}} + \sum_{(x,r)\in D_a}
\mathrm{sigmoid}(y\theta_a^{\top} x) \mathrm{sigmoid}(-y\theta_a^{\top} x) ) xx^\top
\end{align*}
二次近似した事後分布は、その形から$\mathrm{MultiNorm}(\theta_a |\hat{\theta}_a,H(\hat{\theta}_a )^{-1})$に従うことがわかります。
アルゴリズム
- $\mu_a\leftarrow 0, \Sigma_a\leftarrow \lambda I, \forall a$
- 学習ループ
- $D_a\leftarrow\emptyset, \forall a$
- ミニバッチ蓄積ループ
- 特徴ベクトル$x$を受け取る
- $\tilde \theta _a\sim\mathrm{MultiNorm}(\theta_a|\mu_a,\Sigma_a),\forall a$
- $\tilde{a}=\arg\max_a x^\top\tilde{\theta}_a$
- 腕$\tilde{a}$を提示して報酬$r$を受け取る
- $D_a\leftarrow D_a \cup \{(x,r)\}$
- $\hat \theta_a\leftarrow \arg\min_{\theta_a} \frac{(\theta_a-\mu_a)^{\top} \Sigma_a^{-1}(\theta_a-\mu_a)}{2} - \sum_{(x,r)\in D_a} \log\mathrm{sigmoid}(y\theta_a^{\top} x), \forall a$
- $\mu_a\leftarrow\hat\theta_a, \Sigma_a\leftarrow H(\hat\theta_a)^{-1}, \forall a$
論文内では$\Sigma_a$を対角行列に限定したアルゴリズムが示されていますが、一般化して示してみました。
LogisticTSは内部で最適化問題を解く必要があるため、他のアルゴリズムと異なり、完全な差分計算ができません。
毎回全データを見る最適化問題を解くのは現実的ではないので、前回の計算結果を事前分布とした最適化問題を解くようにしています。
実際にサービス実装する場合も、その都度計算すると重いため、データが溜まったタイミングで学習するような工夫が必要になるケースがあります。
アルゴリズム内で、最適化問題を解く部分がありますが、シンプルなニュートン法(ステップ幅1)だと振動して収束しないことがありました。
そのため、更新幅を調整しながら目的関数が必ず下がるように学習していく必要があります。
参考文献
LogisticPGTS
LogisticTSでは、事後分布を二次近似してサンプリングしました。
PGTSでは、PG分布(PolyaGamma分布)を使いギブスサンプリングすることで所望のサンプリング結果を得ます。
ギプスサンプリングとは、直接サンプリングが難しい確率分布の代わりに、それを近似したサンプル列を生成するMCMC法(マルコフモンテカルロ法)です。
アルゴリズム
- $b_a\leftarrow 0, B_a\leftarrow I, \forall a$
- 学習ループ
- $D_a\leftarrow\emptyset, \forall a$
- ミニバッチ蓄積ループ
- 特徴ベクトル$x$を受け取る
- $\tilde \theta _a\sim\mathrm{MultiNorm}(\theta_a|b_a,B_a),\forall a$
- $\tilde{a}=\arg\max_a x^\top\tilde{\theta}_a$
- 腕$\tilde{a}$を提示して報酬$r$を受け取る
- $D_a\leftarrow D_a \cup \{(x,r)\}$
- 各腕$a$に対してループ
- $\theta\sim\mathrm{MultiNorm}(\theta_a|b_a,B_a)$
- $X\leftarrow [x_1,\ldots,x_i,\ldots,x_{|D_a|}]^\top$
- $\kappa\leftarrow [r_1-1/2,\ldots,r_i-1/2,\ldots,r_{|D_a|}-1/2]^\top$
- $M$回ループ
- $\omega_i\sim\mathrm{PG} (1,x_i^\top{\theta}), \forall (x_i,r_i)\in{D}_a$
- $\Omega\leftarrow\mathrm{diag}(\omega_1,\ldots,\omega_i,\ldots,\omega_{|D_a|})$
- $V\leftarrow (X^\top\Omega X+B^{-1})^{-1}$
- $m\leftarrow V(X^\top\kappa+B^{-1}b)$
- $\theta\sim\mathrm{MultiNorm}(\theta_a|m,V)$
- $b_a\leftarrow m, B_a\leftarrow V$
$M$の値は、論文内では1や100といった値が使われていました。
こちらも、LogisticTSと同様に、完全な差分計算ができないのでミニバッチで表現してみました。
なお、PG分布からのサンプリングにはpolyagammaというライブラリがあります。
参考文献
- PG-TS: Improved Thompson Sampling for Logistic Contextual Bandits
- [論文紹介] PG-TS: Improved Thompson Sampling for Logistic Contextual Bandits
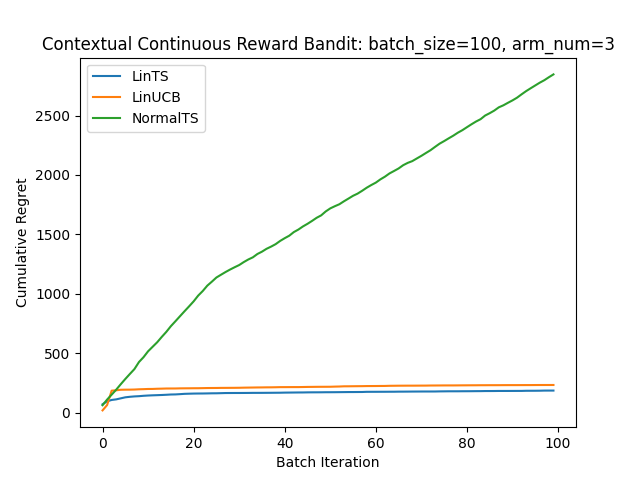
実験
0/1報酬のケースに、真のパラメータを用意してシミュレーションし、これまで紹介したアルゴリズムを適用してみました。
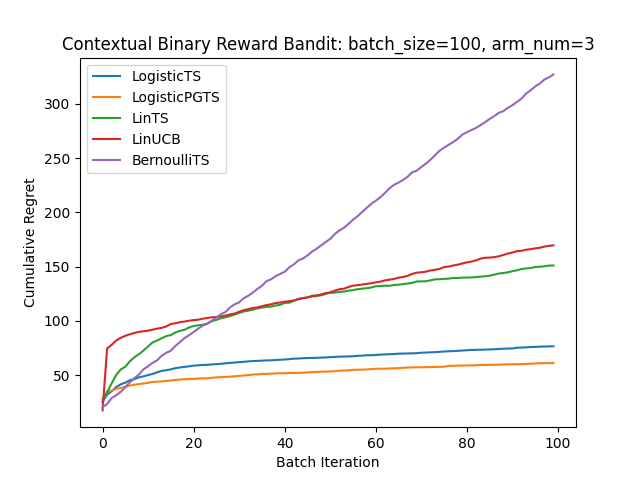
BernoulliTSはベースラインとしてcontextを考慮しない普通のバンディットを置いてます。
また、あえて連続を仮定したモデルも適用してみました。
当然ですがモデルの仮定に合ったLogistic系が強いですね。
このLogisticの2つは実行結果によっては入れ替わったりするので実はあまり大差が無いのかもしれません。
次に、あえてモデルの仮定を無視して、線形モデルの表現力を試してみました。
腕に対応するベクトルを用意して、「ランダムに生成した特徴ベクトルは最も近いベクトルの腕を最も好む」という設定にしました。(特徴ベクトルを用意してクラスタリング後、クラスタごとに好む腕を設定したようなイメージ)
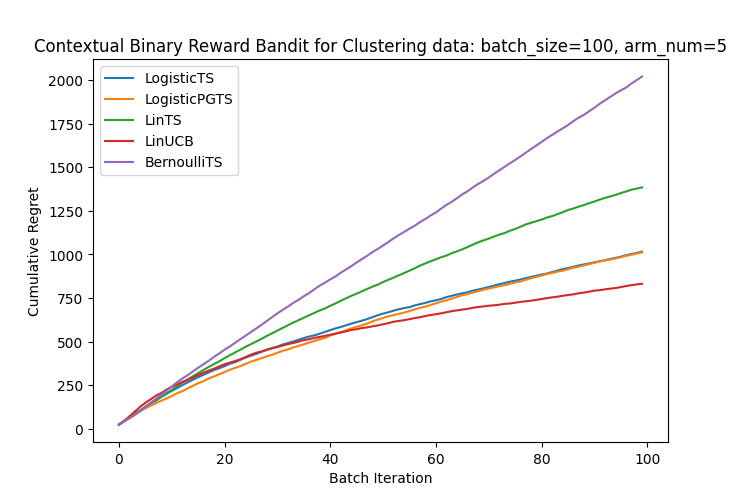
学習後に1000サンプル与えてみると、各グループで最も良い腕を選ぶように学習できていることが確認できました。
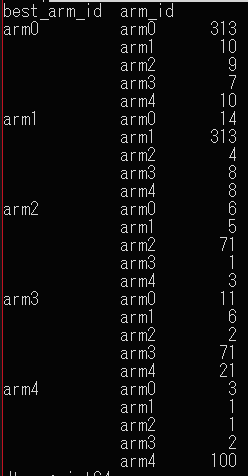
意外と線形でも表現力ありますね。
実データへの適用について
実データに適用する際は、事前に仮定したモデルに当てはまるかどうかわからないため、モデルの表現力が試されます。
ある実データで実験をしていたところ、線形モデルでは 切片項(バイアス項) を入れないとうまく行かないケースがありました。(ここに気づかず時間を溶かしました)
バイアス項は、単純には特徴ベクトル$x$に1を与えればよいので簡単に導入できます。(厳密には切片項にも正則化がかかるが)
実データに適用する際は、過去のログデータから集計した値を腕の好み具合としてシミュレーションしてみることが重要そうです。
Cascading Bandit
ここまでのbanditでは1つの腕を提示してその報酬をもとにベストな腕を見つけようとしてきました。
Cascading Banditでは、順序付きのアイテムを提示してフィードバックをもらうことにより、最適な順序を求めます。
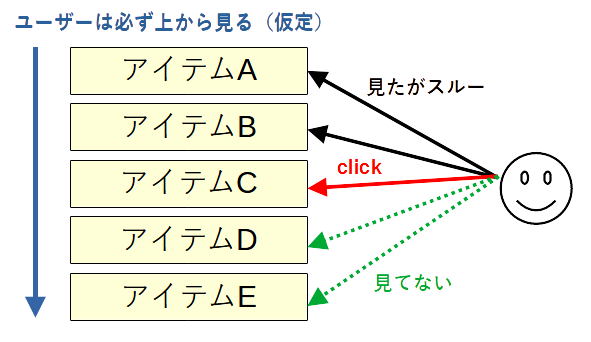
- 順序を最適化するバンディット
- 位置によるバイアスを考慮
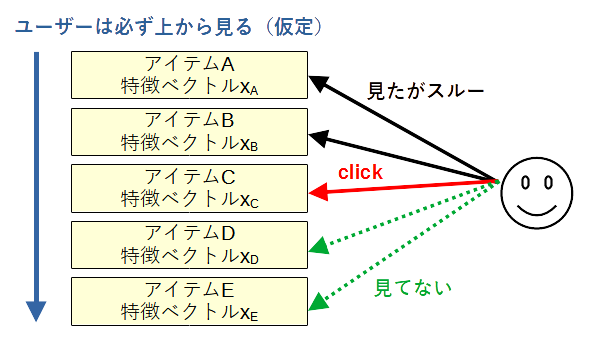
- 仮定
- ユーザーは並んだアイテムを上から順に見る
- ユーザーがアイテムを好んでいた場合は必ずクリックを行う
- クリックされたアイテム以降のアイテムはユーザーに見られていない
- $L$個のアイテムのうち$K$個のアイテムを順序付きで提示する
補足
- 各アイテム$e$の好み確率$P(e)$は、それぞれ独立なベルヌーイ分布に従う
- 提示した$K$個のアイテムが少なくとも1つクリックされる確率$1-\prod_{e\in 提示したアイテム集合} (1-P(e))$を最大化する
アルゴリズム
CascadeUCB
UCB戦略では、アイテム$e$について、次のUCBが大きい順に上から$K$個を並べます。
$$
U(e)=\frac{eのクリック数}{eの観測回数}+\sqrt{\frac{1.5\log(全体試行回数)}{eの観測回数}}
$$
観測回数は、次のルールでカウントされます。
- クリックされたアイテム以上のアイテムを観測したこととする
- どれもクリックされなければ、提示していた$K$個のアイテム全てを観測したこととする
全体試行回数は、アイテムリストを提示した回数です。
論文内では記号がたくさん登場してややこしいですが、紐解くと単純でした。
CascadeKL-UCB
同論文でCascadeUCBの代わりに、以下の基準も提案されていました。
\begin{split}
U(e)=\max\{q\in[eのクリック率,1] \mid& (eの観測回数)\times D_{\rm KL}\left(eのクリック率\mid\mid q\right)\\
&\le \log 全体試行回数 + 3\log\log 全体試行回数\}
\end{split}
$D_{\rm KL}(p\mid\mid q)$は、平均pに従うベルヌーイ分布と平均qに従うベルヌーイ分布のKLダイバージェンスで、
$$
D_{\rm KL}(p\mid\mid q)=p\log\frac{p}{q}+(1-p)\log\frac{1-p}{1-q}
$$
です。(ただし、$0 \log 0 = 0 \log (0/0)= 0, x \log (x/0) = \infty$)
$D_{\rm KL}(p\mid\mid q)$を$q$の関数として見ると、$q\in[p, 1]$の範囲で強凸で単調増加関数なので、$U(e)$をニュートン法(方程式の解を求める手法)で求めることができます。
今回はそもそものシンプルなKL-UCBを紹介しなかったので、詳細は論文に任せます。
参考文献
- Cascading Bandits: Learning to Rank in the Cascade Model
-
The KL-UCB Algorithm for Bounded Stochastic Bandits and Beyond
- シンプルなバンディットのKL-UCB基準です
- Cascade Model に適用する Bandit Algorithms の理論と実装
実験
こちらも真の確率を仮定してシミュレーションしてみました。
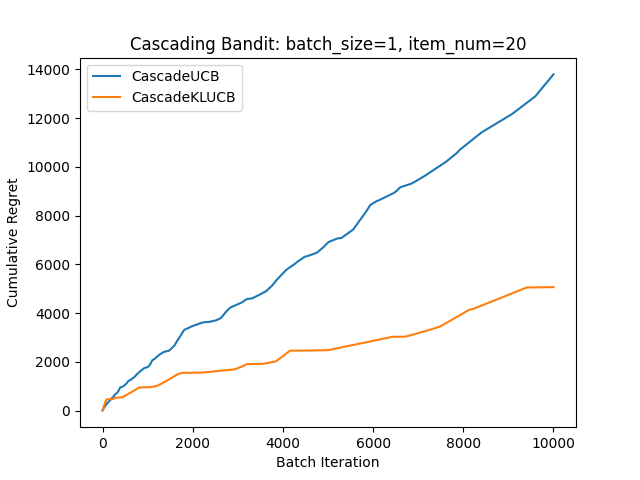
確率の積になるとリグレットが分かりづらいため、logをとって計算してます。
この実験ではKL-UCB強いですが、場合によるみたいです。
また、KL-UCBは計算が重いです。
Contextual Cascading Bandit
ベクトルを持ったアイテム順序を最適化するバンディットです。
ユーザーではなく、アイテムが特徴ベクトル$x_e$を持ちます。
これにより、アイテム数が多い場合でも学習が進みます。
ここでも線形モデルのみ扱います。
各アイテム$e$の好み確率を$\theta^\top x_e$で回帰します。
$\theta$はアイテム間で共通です。
ユーザーごとのパーソナライズの話はこちら↓
アルゴリズム
CascadeLinTS
LinTSとCascadingをあわせたような式が出てきます。
ここまで読んだ方なら見たことある形なので、アルゴリズムだけ記載します。
アルゴリズム
- $A\leftarrow I, b\leftarrow 0$
- ループ
- $\hat\theta\leftarrow \sigma^{-2}A^{-1}b$
- $\tilde \theta\sim \mathrm{MultiNorm}(\theta|\hat\theta, A^{-1})$
- $\tilde\theta^\top x_e$の上位$K$個を大きい順に提示
- $k$番目がクリックされた情報を受け取る
- クリックされたところまでの上位$k$個のアイテム$e$について更新: $A\leftarrow A+\sigma^{-2}x_ex_e^\top$(クリックされなければ$K$個全てを更新)
- クリックされた$k$番目のアイテム$e$について更新: $b\leftarrow b+x_e$
なお、$A^{-1}$の計算は、毎回ランク1行列による修正なため、次のように更新できます。
$$
A^{-1}\leftarrow A^{-1}-\frac{A^{-1}x_e x_e^\top A^{-1}}{x_e^\top A^{-1}x_e+\sigma^2}
$$
CascadeLinUCB
LinUCBとCascadingをあわせたような式が出てきます。
ここまで読んだ方なら見たことある形なので、アルゴリズムだけ記載します。
アルゴリズム
- $A\leftarrow I, b\leftarrow 0$
- ループ
- $\hat\theta\leftarrow \sigma^{-2}A^{-1}b$
- $U(e)\leftarrow \min\{\hat\theta^\top x_e+\alpha\sqrt{x_e^\top A^{-1}x_e},1\},\forall e$
- $U(e)$の上位$K$個を大きい順に提示
- $k$番目がクリックされた情報を受け取る
- クリックされたところまでの上位$k$個のアイテム$e$について更新: $A\leftarrow A+\sigma^{-2}x_ex_e^\top$(クリックされなければ$K$個全てを更新)
- クリックされた$k$番目のアイテム$e$について更新: $b\leftarrow b+x_e$
参考文献
実験
各アイテム$e$の好み確率を$\mathrm{sigmoid}(x_e^\top \theta^*)$と設定し、実験してみました。(モデルの仮定とは異なりますが)
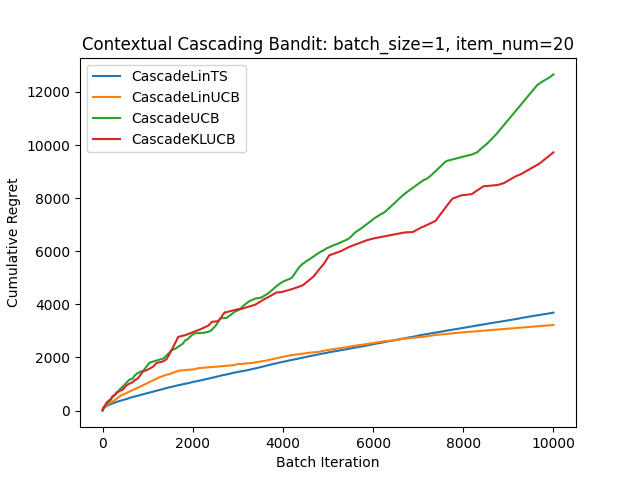
確率の積になるとリグレットが分かりづらいため、logをとって計算してます。
ベースラインとしてcontextを考慮しないCascading Banditも2つ入れています。
モデルの仮定と異なるためTSが弱くなっていると思われます。
あとがき
主に4つのタイプのバンディットを学びました。
- Bandit: 最適な選択肢を見つける
- Contextual Bandit: 各ユーザーごとに最適な選択肢を見つける
- Cascading Bandit: アイテム順序を最適化する
- Contextual Cascading Bandit: ベクトル表現を持つアイテム順序を最適化する
実装自体は重くないので、実際にシミュレーション実験をしてみて適切なアルゴリズムを選択するのが重要だと思いました。