【Rust】ABC424まとめ（A~C）

AtCoder Beginner Contest 424

バーチャル参加し、ABC3完（34分1ペナ）でした。
今回はA~Cまでをまとめていきます。

A - Isosceles

所与の条件が座標だったら大変だなと思いつつ、よく読むと辺の長さなのでシンプルでした。
$A=B, B=C, C=A$のうち、いずれかの条件を満たせばその時点で二等辺三角形が成立します。

use proconio::input;

fn main() {
    input! {
        a: usize,
        b: usize,
        c: usize,
    }

    if a == b || b == c || c == a {
        println!("Yes");
    }else {
        println!("No");
    }
}

B - Perfect

$N\times M$配列$\text{arr}$を以下のように定義します。

$$ \text{arr}_{i,j}:=i番目の人がj問目の問題に正解したかどうか $$

最初に、$(i, j) \in [1, N] \times [1, M]$について、$\text{arr}_{i,j} = 0 $で初期化しておきます。

その後$K$回にわたり、人$A_i$が問題$B_i$に正解するというイベントが発生するため、都度
$\text{arr}_{A_i,B_j}=1$に変更します。

このとき、すべての$j$について$\text{arr}_{A_i,j}=1$が成立すれば$A_i$は全問正解したことになるので、出力用の配列にpushしましょう。
最後に、その配列を半角スペースで結合すれば終了です。

use itertools::Itertools;
use proconio::input;

fn main() {
    input! {
        n: usize,
        m: usize,
        k: usize,
        problems: [(usize, usize); k],
    }

    let mut arr = vec![vec![0; m]; n];
    let mut ans = vec![];
    for &(x, y) in problems.iter() {
        arr[x - 1][y - 1] = 1;
        if arr[x - 1].iter().all(|&v| v == 1) {
            ans.push(x);
        }
    }

    println!("{}", ans.iter().join(" "));
}

C - New Skill Acquired

$(A_i, B_i)=(0,0)$の習得済みスキル$i$を起点に、$A_j = i \lor B_j = i$であるようなスキル$j$へと広がっていくイメージなので、BFS(幅優先探索)というアルゴリズムを用います。特に、$(A_i, B_i)=(0,0)$である複数の始点でスタートする場合は多始点BFSと呼ばれることがあります。

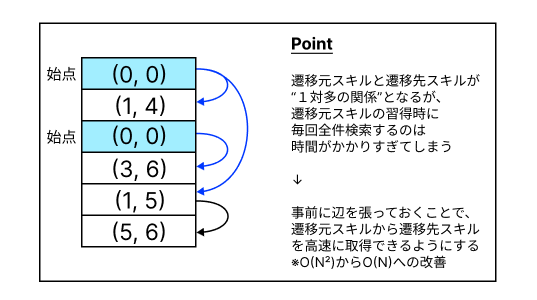
以下の図をイメージしていただけると幸いです。
始点が複数あり、有向辺に沿って習得済みのスキルが広がっている様子がわかると思います。

▼本問における多始点BFSのイメージ

ここで、遷移元スキルと遷移先スキルが１対多の関係となっていることにも注意してください。
この場合、遷移元スキル習得時に遷移先のスキルを都度全件検索すると当然$N$回の計算が必要となり、全体として$O(N^2)$の計算量となるため実行時間制限に間に合いません。

したがって、一つ工夫として事前に遷移元スキルから遷移先スキルへの辺を張っておくことで、ある遷移元スキルを習得した時に連鎖的に習得可能な遷移先スキルだけを取得することができるようになります。辺の個数とスキルの個数がともに$N$であるため$O(N)$の全体計算量となり、これは十分に高速です。

use proconio::input;

fn main() {
    input! {
        n: usize,
        skills: [(usize, usize); n],
    }
    let mut can_acquire = vec![vec![]; n];
    for (i, &(a, b)) in skills.iter().enumerate() {
        if a != 0 {
            can_acquire[a - 1].push(i);
        }
        if b != 0 {
            can_acquire[b - 1].push(i);
        }
    }

    fn bfs(skills: &Vec<(usize, usize)>, visited: &mut Vec<bool>, can_acquire: &Vec<Vec<usize>>) {
        let mut stack = vec![];
        for i in 0..skills.len() {
            if skills[i] == (0, 0) && !visited[i] {
                visited[i] = true;
                stack.push(i);
            }
        }

        while let Some(i) = stack.pop() {
            for &j in &can_acquire[i] {
                if !visited[j] {
                    visited[j] = true;
                    stack.push(j);
                }
            }
        }
    }
    let mut visited = vec![false; n];
    bfs(&skills, &mut visited, &can_acquire);
    let ans = visited.iter().filter(|&&x| x).count();
    println!("{}", ans);
}

まとめ

D問題は3x3,3x2,2x3,2x2の長方形領域を順に見ていき、中央を白で塗りつぶすことで最小を達成できると思っていましたが、これは完全に嘘解法で、正解はbitDPというアルゴリズムでした。
E問題は決め打ち二分探索という方針は当たりましたが実装しきれず。
最近の水色問題は何かと難しい気がしますね、少し前は全探索でも全然水色だったと思いますが時代が変わりました。