目的
- 時系列データときたらとりあえずRNN!、LSTM!!っていう感じだったのですが、ARIMAとかSARIMAなるものを知り自分の引き出しに加えたいということで勉強。
- ライブラリ使ってそれにぶち込むのは簡単だろうけど、一応理論も知っておきたいということで、本を購入した。
- 沖本竜義先生の『経済・ファイナンスデータの計量時系列分析』という本。2010年の本です。
データ
読みながら手も動かしていこうということでとりあえずTOPIXのヒストリカルデータを使うことにした。
https://quotes.wsj.com/index/JP/TOKYO%20EXCHANGE%20(TOPIX)/180460/historical-prices
WSJのHPからダウンロードできた。
とりあえず欠損値はない模様。
期間は2008年12月30日から2019年11月29日まで。
配当落ち調整なしの4本値のヒストリカルデータ。
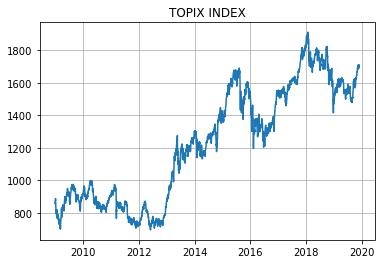
終値をプロットすると下図のような感じ。
ちょうどリーマンショック直後の1,000pt割れの時期からアベノミクスを経てというような期間です。
日次リターンは以下の通り。日次なので大した差は出ないだろうが対数リターン($\Delta \log{y_t} = \log{(y_t)} - \log{(y_{t-1})}$)を使用した。
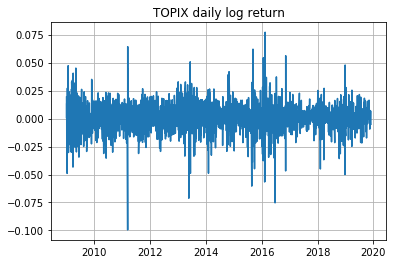
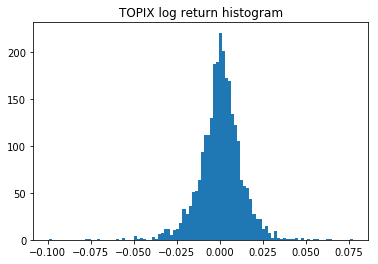
最大の下げを記録したのは2011年3月15日で、$\Delta \log{y_t} = -0.0995$となっている。前日引け前15分くらいのところで東北地方太平洋沖地震が起きたのが原因。
各種統計量
平均
$\bar{y} = \frac{1}{T}\displaystyle{\sum_{t=1}^{T}y_t}$
tpx_return = np.log(tpx['close'].values)[1:] - np.log(tpx['close'].values)[:-1]
tpx_return.mean()
0.00025531962222667643
自己共分散(auto-covariance)
$\hat{\gamma}_k = \frac{1}{T} \displaystyle{\sum_{t=k+1}^{T}}(y_t-\bar{y})(y_{t-k}-\bar{y}),\quad k = 0,1,2,...$
import statsmodels.api as sm
sm.tsa.stattools.acovf(tpx_return, fft=True, nlag=5)
array([ 1.57113176e-04, 1.16917913e-06, 3.48846296e-06, -4.67502133e-06, -5.31500282e-06, -2.82855375e-06])
statsmodelsのライブラリに慣れていないので一応手でも確認。
# k=0
((tpx_return-tpx_return.mean())**2).sum() / len(tpx_return)
0.00015711317609153836
# k=4
((tpx_return-tpx_return.mean())[4:]*(tpx_return-tpx_return.mean())[:-4]).sum() / len(tpx_return)
-5.315002816332674e-06
自己相関係数(auto-correlation)
$\hat{\rho}_k = \frac{\hat{\gamma}_k}{\hat{\gamma}_0},\quad k=1,2,3,...$
sm.tsa.stattools.acf(tpx_return)[:5]
array([ 1. , 0.00744164, 0.0222035 , -0.02975576, -0.03382913])
先ほどの$k=0$と$k=4$の結果を使って確認すると、
-5.315002816332674e-06 / 0.00015711317609153836
-0.03382913482212345
ということでライブラリはイメージした通りの計算をしてくれている様子。
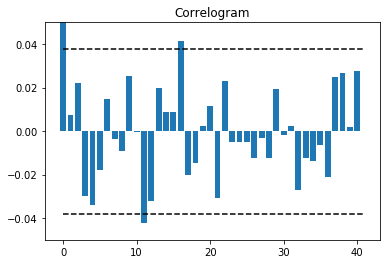
コレログラムも描いてみる。コレログラムとは自己相関係数をグラフにしたもののこと。
autocorr = sm.tsa.stattools.acf(tpx_return)
ci = 1.96 / np.sqrt(len(tpx_return))
plt.bar(np.arange(len(autocorr)), autocorr)
plt.hlines([ci,-ci],0,len(autocorr), linestyle='dashed')
plt.title('Correlogram')
plt.ylim(-0.05,0.05)
plt.show()
CI(confidence interval)とは信頼区間のことで、データが互いに独立で同一の分布に従う時、$\hat{\rho}_k$が漸近的に平均$0$、分散$\frac{1}{T}$の正規分布に従うという性質を利用して両側95%を計算している。
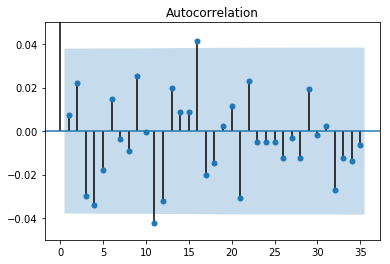
ライブラリを使うとこんな感じ。オシャレ。
sm.graphics.tsa.plot_acf(tpx_return)
plt.ylim(-0.05,0.05)
plt.show()
得られた数字について少し考えてみる。
$\hat{\rho}_{k=11}=-0.0421, \quad \hat{\rho}_{k=16}=0.0415$
の2回 $CI=0.0379$ をわずかながら上回っている。
特に $\hat{\rho}_{k=12}=-0.0323$ もマイナスの値となっており、1回相場が上昇・下落を始めても一旦そのモメンタムが2週間程度で終わることを示唆していると捉えることができるかもしれない。
かばん検定(portmanteau test)
複数の自己相関係数がすべて0であるという帰無仮説を検定する手法。
$H_0 : \rho_1 = \rho_2 =\quad ... \quad= \rho_m = 0$
ここでは本で紹介されているLjung and Box(1978)の統計量を用いて検定を行ってみる。下の$Q(m)$とカイ2乗分布の95%点を比較するというアプローチである。
$Q(m) = T(T+2)\displaystyle{\sum_{k=1}^{m}}\frac{\hat{\rho}^2_k}{T-k} \sim \chi^2(m)$
また、P値という統計量も定義されており、カイ2乗分布に従う確率変数が$Q(m)$より大きな値をとる確率を示したものである。すなわち、有意水準5%とすれば、P値が0.05より小さいとき$H_0$は棄却される。
$m$の値については、$m \approx \log{(T)}$が目安とされるようだが、複数の$m$に対して検定を行い総合的に判断するのが一般的なようである。
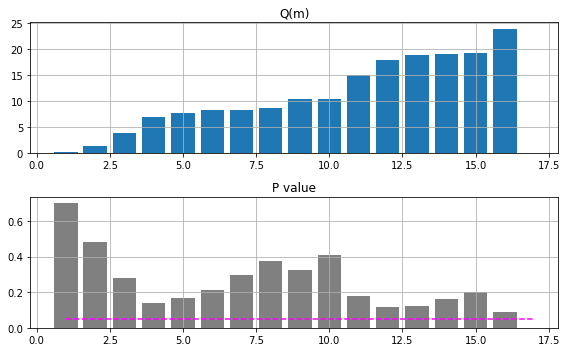
まずはstatsmodelsのライブラリを使うパターンから。
$m \approx \log{(T)} = 7.89$ ということで、とりあえずラグは16までの範囲で考えてみる。
lvalue, pvalue = sm.stats.diagnostic.acorr_ljungbox(tpx_return)
$m$がどの値でもP値は0.05以下にはならず、TOPIXの日次変化率は自己相関を持つとは言えないという結果となった。まあ相場はそんなに単純なものではないってことですね。
最後に自分の理解を深めるためライブラリなしでも試してみる。
from scipy.stats import chi2
def Q_func(data, max_m):
T = len(data)
auto_corr = sm.tsa.stattools.acf(data)[1:]
lvalue = T*(T+2)*((auto_corr**2/(T-np.arange(1,len(auto_corr)+1)))[:max_m]).cumsum()
pvalue = 1 - chi2.cdf(lvalue, np.arange(1,len(lvalue)+1))
return lvalue, pvalue
同じ結果が得られていることを確認。
l_Q_func, p_Q_func = Q_func(tpx_return,max_m=16)
l_sm, p_sm = sm.stats.diagnostic.acorr_ljungbox(tpx_return, lags=16)
((l_Q_func-l_sm)**2).mean(), ((p_Q_func-p_sm)**2).mean()
(0.0, 7.824090399073146e-34)
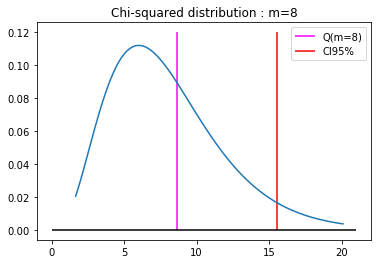
$m=8$のケースを細かく見てみると、
T = len(tpx_return)
auto_corr = sm.tsa.stattools.acf(tpx_return)[1:]
lvalue = T*(T+2)*((auto_corr**2/(T-np.arange(1,len(auto_corr)+1)))[:8]).sum()
print(lvalue)
8.604732778577853
1-chi2.cdf(lvalue,8)
0.37672860496603844
ということで、帰無仮説を棄却することはかなり難しいことが分かった。