はじめに
今回はMP3、Vorbis(Ogg)、 AAC等の音声圧縮形式が使用している修正離散コサイン変換を使用して音声データの圧縮、伸長をJavaScriptとWebAudioを使用して実装して見ました。
https://redlily.github.io/training-webaudio-compression
Chrome推奨
設計
設計、実装方針
- JavaScriptとWebAudioで圧縮、伸長、再生が可能な実装を行う。
- 音声に関わる実装はOSSのライブラリを一切使わずに自力で実装を行う。
- MP3、Vorbis(Ogg)、AACの音声圧縮形式が使用している修正離散コサイン変換を用いた実装を行う。
- 音質をある程度保ちながら16bitで量子化された無圧縮データと比較して1/8程度まで圧縮を行う。
- なるだけ単純な実装で圧縮率を上げる。(エンコーダ、デコーダの実装をあわせて1000行程度)
- 今回は音声圧縮のノウハウの獲得が目的なので可逆圧縮の導入は見送り。
圧縮・再生用のアプリケーションの設計
音声の読み込み、圧縮、伸長、再生を行うアプリケーション部分の設計概要となります。
圧縮
- 音声データを読み込む
- AudioContext.decodeAudioDataを使用して音声データを波形データに変換する。
- 波形データを独自の圧縮形式にエンコードする。
- ArrayBufferにデータを変換し、ダウンロード可能にする。
伸長、再生
- 独自の圧縮済みの音声データを読み込む。
- ScriptProcessorNodeを生成する。
- 独自の圧縮済み音声データを波形データにデコードする。
- 波形データをスピーカーに出力する。
エンコーダ・デコーダの設計
音声の波形データを実際にエンコード、デコードするコーデックの設計概要となります。
エンコード
- 波形データを入力
- 窓関数を適用
- 修正離散コサイン変換を適用
- 周波数を間引く
- 対数量子化
- 圧縮済みデータを出力
デコード
- 圧縮済みデータを入力
- 対数を指数関数で線形の数値に戻す
- 間引かれた周波数データを修正離散コサイン変換用の配列に展開
- 逆修正離散コサイン変換を適用
- 窓関数を適用
- 波形データを出力
データ設計
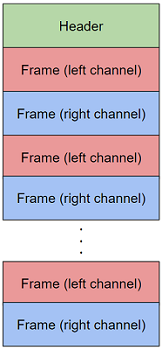
基本構造
大枠の設計はヘッダーがデータの先頭あり、その後に固定長のフレームの配列が連なるといった単純な構造となります。
ヘッダ
| 変数名 | 型 | 説明 |
|---|---|---|
| MAGIC_NUMBER | UINT32 | マジックナンバー、"WAM0"が固定値 |
| DATA_SIZE | UINT32 | データのバイトサイズ |
| DATA_TYPE | UINT32 | 拡張用のデータタイプ、"SMD0"が固定値 |
| VERSION | UINT32 | データのバージョン |
| SAMPLING_RATE | UINT32 | サンプリングレート |
| CHANNEL_SIZE | UINT32 | チャネル数、1がモノラル、2がステレオ |
| SAMPLE_COUNT | UINT32 | データに含まれるサンプル数 |
| FREQUENCY_RANGE | UINT16 | 周波数ブロックのサイズ |
| FREQUENCY_UPPER_LIMIT | UINT16 | 周波数ブロックの上限値 |
| FREQUENCY_TABLE_SIZE | UINT16 | 周波数テーブルのサイズ |
| - | UINT16 | バイトアライメント調整用の領域、今後の拡張次第では何か数値が入るかも |
| FRAME_COUNT | UINT32 | データに含まれるフレーム数 |
| FRAME_DATA | FRAME[CHANNEL_SIZE * FRAME_COUNT] | フレーム配列、チャネル数が2の場合、左、右とフレームが並ぶ |
フレーム
| 変数名 | 型 | 説明 |
|---|---|---|
| MASTER_SCALE | UINT32 | このフレームの主音量 |
| SUB_SCALES | UINT4[8] | 8つの周波数帯用の音量を調整するためのスケール値 |
| ENABLE_FREQUENCIES | 1bit[FREQUENCY_UPPER_LIMIT] or ceil(log_2(FREQUENCY_UPPER_LIMIT))bit [FREQUENCY_UPPER_LIMIT] |
周波数の有効無効を収納した1bitのフラグ配列、もしくは有効な周波数のインデックスを収納した配列 バイト数の小さい方を使用し4バイトアライメントに適合するサイズにする |
| FREQUENCY_VALUES | 4bit[FREQUENCY_TABLE_SIZE] | 有効な周波数の対数で符号化された数値 |
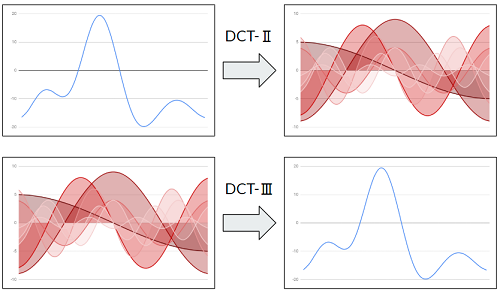
離散コサイン変換(discrete cosine transform)
N個のサンプルデータに対してN個の0からN-1の異なる周波数のcos波に信号を分解する事が出来る変換になります。
JPEGはこの離散コサイン変換を利用してデータの圧縮を行っています。
下記はイメージ図となります。
離散コサイン変換タイプ2(DCT-Ⅱ もしくは DCT)の式
y_k = \sum^{N-1}_{n=0} x_n \cos(\frac{\pi}{N}(n + \frac{1}{2})k)
離散コサイン変換タイプ3(DCT-Ⅲ もしくは 逆DCT)の式
x_n = \frac{1}{2} y_0 + \sum^{N-1}_{k=1} y_k \cos(\frac{\pi}{N}(n + \frac{1}{2})k)
高速化
離散コサイン変換はN^2のオーダーで計算量が増えてしまう特性があります。そのまま離散コサイン変換を数式通り実装してしまうとかなり遅いものになってしまうので高速化アルゴリズムを導入します。
今回はLee型DCTと呼ばれる高速化手法を下記の論文とを参考に実装しました。
これを適用する事によりN log Nのオーダーの計算量ですみます。
A New Algorithm to Compute the Discrete Cosine Transform - BYEONG GI LEE
Design and Implementation of an MPEG-1 Layer III Audio Decoder
離散コサイン変換タイプ2(DCT-Ⅱ)の高速化の実装例
// 離散コサイン変換、タイプII
// n - サンプル数、2のべき乗である必要がある
// x - n個のサンプルの配列
static dctII(n, x) {
// バタフライ演算
let rad = Math.PI / (n << 1);
for (let m = n, mh = m >> 1; 1 < m; m = mh, mh >>= 1) {
for (let i = 0; i < mh; ++i) {
let cs = 2.0 * Math.cos(rad * ((i << 1) + 1));
for (let j = i, k = (m - 1) - i; j < n; j += m, k += m) {
let x0 = x[j];
let x1 = x[k];
x[j] = x0 + x1;
x[k] = (x0 - x1) * cs;
}
}
rad *= 2.0;
}
// データの入れ替え
FastDCT.swapElements(n, x);
// 差分方程式
for (let m = n, mh = m >> 1, mq = mh >> 1; 2 < m; m = mh, mh = mq, mq >>= 1) {
for (let i = mq + mh; i < m; ++i) {
let xt = (x[i] = -x[i] - x[i - mh]);
for (let j = i + mh; j < n; j += m) {
let k = j + mh;
xt = (x[j] -= xt);
xt = (x[k] = -x[k] - xt);
}
}
}
// スケーリング
for (let i = 1; i < n; ++i) {
x[i] *= 0.5;
}
}
離散コサイン変換タイプ3(DCT-Ⅲ)の高速化の実装例
// 離散コサイン変換、タイプIII
// n - サンプル数、2のべき乗である必要がある
// x - n個のサンプルの配列
static dctIII(n, x) {
// スケーリング
x[0] *= 0.5;
// 差分方程式
for (let m = 4, mh = 2, mq = 1; m <= n; mq = mh, mh = m, m <<= 1) {
for (let i = n - mq; i < n; ++i) {
let j = i;
while (m < j) {
let k = j - mh;
x[j] = -x[j] - x[k];
x[k] += x[j = k - mh];
}
x[j] = -x[j] - x[j - mh];
}
}
// データの入れ替え
FastDCT.swapElements(n, x);
// バタフライ演算
let rad = Math.PI / 2.0;
for (let m = 2, mh = 1; m <= n; mh = m, m <<= 1) {
rad *= 0.5;
for (let i = 0; i < mh; ++i) {
let cs = 2.0 * Math.cos(rad * ((i << 1) + 1));
for (let j = i, k = (m - 1) - i; j < n; j += m, k += m) {
let x0 = x[j];
let x1 = x[k] / cs;
x[j] = x0 + x1;
x[k] = x0 - x1;
}
}
}
}
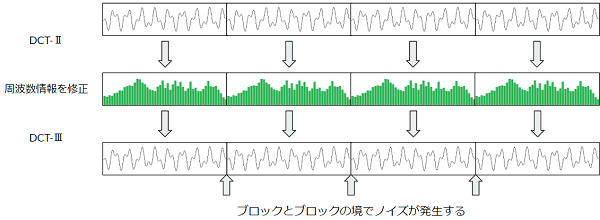
離散コサイン変換の欠点
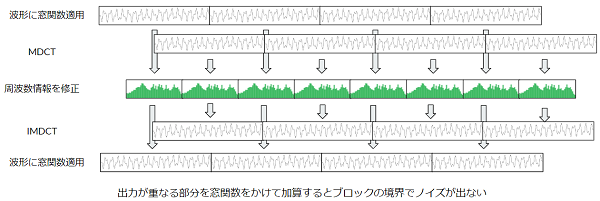
離散コサイン変換を音声圧縮に使用する場合、サンプルを適当なサイズのブロックに区切って周波数変換をかけて、そのデータに対し非可逆圧縮をかけていく事になるのですが、この方法で非可逆圧縮をかけて元に戻そうとした場合、ブロックとブロックの境で高周波数のノイズが発生してしまいます。
この問題は同じく離散コサイン変換を使用するJPEGでもブロックノイズという形で発生します。画像の場合はある程度許容出来る範囲のノイズなのですが音声の場合は聞くに耐えないくらいのノイズが発生するので、この問題に対処する必要があります。
修正離散コサイン変換(modified discrete cosine transform)
離散コサイン変換を音声に適応する上での欠点、変換したブロックとブロックの境界で高周波数のノイズが発生してしまう欠点を窓関数と組み合わせて使用する事により、その欠点を解消することの出来る変換となります。
具体的にはこの変換は解析ブロック半分ずつ重ねて周波数変換を行うことが出来、この重なる部分に対して窓関数をかけてクロスフェードさせる事により解析ブロックと継ぎ目を目立たなくすることが出来ます。
修正離散コサイン変換(MDCT)の式
y_k = \sum^{2N-1}_{n=0} x_n \cos(\frac{\pi}{N}(n + \frac{1}{2} + \frac{N}{2})(k + \frac{1}{2}))
逆修正離散コサイン変換(逆MDCT)の式
x_n = \frac{1}{N} \sum^{N-1}_{k=0} y_k \cos(\frac{\pi}{N}(n + \frac{1}{2} + \frac{N}{2})(k + \frac{1}{2}))
高速化
今回は離散コサイン変換の高速化処理をそのまま流用できるアルゴリズムを下記の論文を参考に実装しました。
Fast IMDCT and MDCT Algorithms— A Matrix Approach Mu-Huo Cheng and Yu-Hsin Hsu
修正離散コサイン変換の高速化の実装例
// 修正コサイン変換(MDCT)
// n - 周波数配列数、2のべき乗である必要がある
// samples - 2n個のサンプル配列、この配列が変換処理の入力元となる
// frequencies - n個の周波数配列、この配列が変換処理の出力先となる
static mdct(n, samples, frequencies) {
// データを結合
let ns1 = n - 1; // n - 1
let nd2 = n >> 1; // n / 2
let nm3d4 = n + nd2; // n * 3 / 4
let nm3d4s1 = nm3d4 - 1; // n * 3 / 4 - 1
for (let i = 0; i < nd2; ++i) {
frequencies[i] = samples[nm3d4 + i] + samples[nm3d4s1 - i];
frequencies[nd2 + i] = samples[i] - samples[ns1 - i];
}
// cos値の変換用の係数をかけ合わせ
let rad = Math.PI / (n << 2);
let i = 0;
let nh = n >> 1;
for (; i < nh; ++i) {
frequencies[i] /= -2.0 * Math.cos(rad * ((i << 1) + 1));
}
for (; i < n; ++i) {
frequencies[i] /= 2.0 * Math.cos(rad * ((i << 1) + 1));
}
// DCT-II
FastDCT.dctII(n, frequencies);
// 差分方程式
for (let i = 0, j = 1; j < n; i = j++) {
frequencies[i] += frequencies[j];
}
}
逆修正離散コサイン変換(Inverse MDCT)の高速化の実装例
// 逆修正コサイン変換
// n - 周波数配列数、2のべき乗である必要がある
// samples - 2n個のサンプル配列、この配列が変換処理の出力先となる
// frequencies - n個の周波数配列、この配列が変換処理の入力元となる
static imdct(n, samples, frequencies) {
// cos値の変換用係数を掛け合わせ
let rad = Math.PI / (n << 2);
for (let i = 0; i < n; ++i) {
frequencies[i] *= 2.0 * Math.cos(rad * ((i << 1) + 1));
}
// DCT-II
FastDCT.dctII(n, frequencies);
// 差分方程式
frequencies[0] *= 0.5;
let i = 0, j = 1;
let nh = n >> 1;
for (; i < nh; i = j++) {
frequencies[j] += (frequencies[i] = -frequencies[i]);
}
for (; j < n; i = j++) {
frequencies[j] -= frequencies[i];
}
// スケーリング
for (let j = 0; j < n; ++j) {
frequencies[j] /= n;
}
// データを分離
let ns1 = n - 1; // n - 1
let nd2 = n >> 1; // n / 2
let nm3d4 = n + nd2; // n * 3 / 4
let nm3d4s1 = nm3d4 - 1; // n * 3 / 4 - 1
for (let i = 0; i < nd2; ++i) {
samples[ns1 - i] = -(samples[i] = frequencies[nd2 + i]);
samples[nm3d4 + i] = (samples[nm3d4s1 - i] = frequencies[i]);
}
}
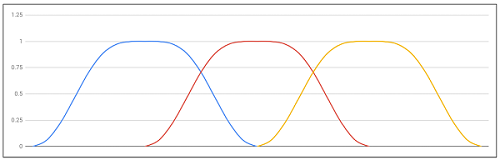
窓関数(windows function)
修正離散コサイン変換のデータの重なった部分を滑らかに結合するために使用します。簡単に言えばクロスフェードさせてデータのブロックとブロックの境を目立たなくするために導入する関数となります。
今回はVorbisで使用されているVorbis窓と呼ばれる窓を使用します。
\omega_x = \sin(\frac{\pi}{2}\sin^{2}\pi x), 0 \leq x \leq 1
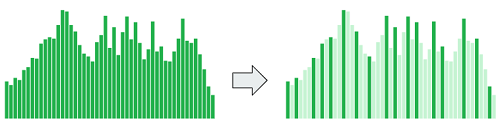
周波数帯の間引き
人間の耳は相対的に大きな音の近くにある周波数帯の小さな音は感知しにくい特性があります。これをマスキング効果といい、これを利用して修正離散コサイン変換で得られた周波数配列からデータを間引きます。
アルゴリズムとしては等ラウドネス曲線等を利用して各周波数の音量を人間の知覚的に平準化、その後マスキング効果による周波数の選定を行えば、より良い結果が得られるのでしょうが、今回は実装は割愛してわかりやすく周波数帯を適当にぶつ切りにして、そのぶつ切りにした周波数帯の中で最も数値の絶対値が大きい周波数を出力候補としました。
この間引により出力する周波数の数を1/4から1/8程度まで減らしても音質を保つ事が出来ます。
周波数の上限を設定
それと人間の耳は高い周波数の音、16000Hz程度から上の周波数帯は聞き取りづらいもしくは聞き取れないようなので、その高い周波数帯のデータは処理対象外とし他の周波数帯に多くのデータを割り当てるようにして圧縮率の向上を図ります。
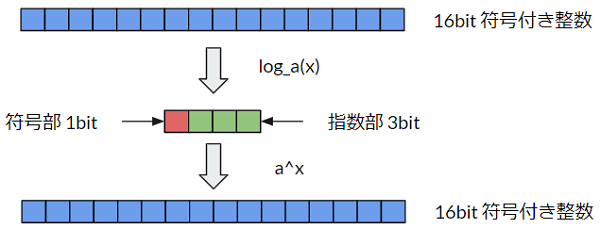
対数による量子化
通常PCMはサンプルデータを線形的な数値で量子化を行いますが、人間は音の知覚が対数関数的である生理学的な特性を利用して非線形的に量子化すると16bit程度の容量が必要なデータを音質を保ちながら符号部1bit、指数部3bitの計4bit程度のデータに圧縮する事が出来ます。これは浮動小数点数で言えば仮数部を取り除いたものと言えます。
今回の実装では対数の底は2を使用しますがデータの設計によって底は決めると良さそうです。例えば8bitでデータを保存する場合は底が2だとbitの幅に対して数値の精度が荒くなったりします。
エンコードの例
y_n = -(\log_2 \frac{|x_n|}{2^{15}})\\
s_n = sgn(x_n)
encodedFrequencies[i] = -Math.log2(Math.abs(inputFrequencies[i]) / (1 << 15));
frequencySigns[i] = inputFrequencies[i] < 0 ? -1 : 1;
デコードの例
x_n = 2^{15} \times 2^{-y_n} \times s_n
outputFrequencies[i] = (1 << 15) * Math.pow(2, -encodedFrequencies[i]) * frequencySigns[i];
スケール値を適用
対数による量子化は音量の大きな音には良いのですが音量が小さな音に対しては波形が歪んでしまいます。
そこで各周波数の最大値をスケール値としてデータに保持します。これは浮動小数点数で言えば仮数部に相当する数値になります。
エンコードの例
y_n = -(\log_2 \frac{|x_n|}{scale})\\
s_n = sgn(x_n)
encodedFrequencies[i] = -Math.log2(Math.abs(inputFrequencies[i]) / scale);
frequencySigns[i] = inputFrequencies[i] < 0 ? -1 : 1;
デコードの例
x_n = scale \times 2^{-y_n} \times s_n
outputFrequencies[i] = scale * Math.pow(2, -encodedFrequencies[i]) * frequencySigns[i];
サブスケール値を適用
対数による量子化により音量の大きな音、小さな音に対応出来るようになりましたが各周波数の精度は周波数全体の最大値に左右されてしまいます。つまり最大値の周波数の音質は良好なものになるのですが、それ以外の周波数帯の音質は有効な数値が小さい分、劣化します。
例えば比較的静かな状態で音量が大きな低音と音量が少し低い高音が同時になっているような場合に高音の周波数帯の音質が低下が顕著になってしまうといったものになります。
そこで各周波数でバンドを区切り、スケール値の補助的な数値を保持します。ここでは対数の数値オフセットを対数化されたサンプルデータに適用することにします。周波数バンドの区切り方は比較的重要なデータが多い低周波数は密にし、高周波数に行くにつれ範囲を大きくとるようにしました。
エンコード時
y_n = -(\log_2 \frac{|x_n|}{Scale}) - sub_k\\
s_n = sgn(x_n)
encodedFrequencies[i] = -Math.log2(Math.abs(inputFrequencies[i]) / mainScale) - subScale[j];
frequencySigns[i] = inputFrequencies[i] < 0 ? -1 : 1;
デコード時
x_n = scale \times 2^{-y_n - sub_k} \times s_n
outputFrequencies[i] = mainScale* Math.pow(2, -encodedFrequencies[i] - subScale[j]) * frequencySigns[i];
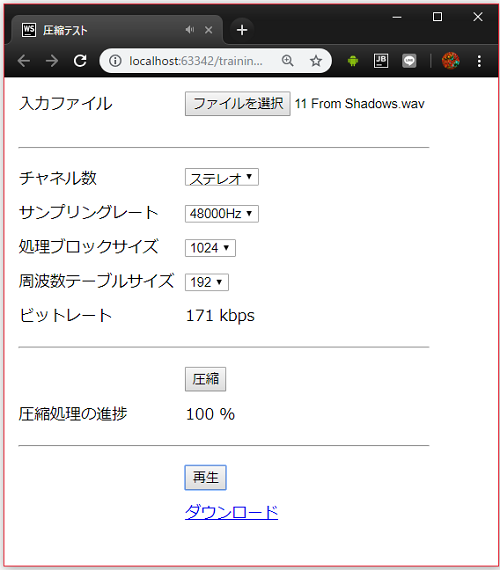
出来上がったもの
UIが貧弱ですが上記のものを全て実装したものがこちらになります。
↓実際に動作するもの
デフォルトの設定で48000Hz、ステレオのデータを周波数、チャネル数を変えずに且つ音質もそこそこ保ったまま、同じ条件のwav形式の無圧縮データと比較して1/10程度のビットレート140kpbs程度のデータ量に圧縮する事が出来ます。
AudioContext.decodeAudioDataの機能でwav形式の他にMP3、Vorbis、AACとブラウザが対応していれば、どんな形式でも圧縮対象のデータとして読み込むことが可能ですが、エンコーダの性能を引き出すには無圧縮のwav形式の使用が推奨です。
感想としてはMP3等の既存の修正離散コサイン変換を利用した音声圧縮には劣るものの個人で設計し実装した割には音質を保って圧縮できるものが出来たかと思っています。
機能
- 圧縮対象のデータ読み込み
- 圧縮済みのデータの読み込み
- 圧縮オプションの選択
- ステレオ、モノラルの選択
- サンプリング周波数の選択
- 処理サンプル数の選択
- 上限周波数の選択
- 周波数の本数の選択
- データの圧縮
- 圧縮済みデータの再生
動作確認済み
- Chrome
- Firefox
- Edge
- Safari (バグあり)
- Android Chrome
- iOS Safari (バグあり)
参考
- 離散コサイン変換
- 修正離散コサイン変換
- 高速離散コサイン変換
- 高速修正離散コサイン変換
- 心理音響学
成果物
- GitHub
- サンプルプログラム
デコーダ、エンコーダの実装の細かい詳細は、この記事の中で書ききれないので知りたい方は上記のソースコードを参照してくれれば有り難いです。