ミニマックス法で最強の3目並べAIを実装する話

Hello, World! あーみーです．

この記事はLife is Tech! Tokai Mentors Advent Calendar 2018 9日目の記事です．

昨年，研究室の勉強会でミニマックス法の実装を担当することになり，せっかくだからQiitaに記事を投稿しようと思いタイトルだけ書いて１年が経ってしまいました．

今回はアドベントカレンダーの力を借りて眠っていた記事を完成させます．

ちなみに，ミニマックス法の実装に再帰関数を用いているため，先日のこの記事は今回の記事を読むための前準備としての意味もありました．

さて，今回題材とするゲームは3目並べです．ゲームシステムと相手AIを実装します．

3目並べ

3目並べは「二人零和有限確定完全情報ゲーム」と呼ばれるゲームに分類されます．
簡単に言うと「勝敗は偶然に左右されず，最善手を打てばどちらかが勝つまたは引き分けになるゲーム」のことです．

他にもリバーシ，チェッカー，チェス，将棋に囲碁などもこのゲームに分類されます．

初めに3目並べというゲームについて定義をしておきます．

3目並べ

3$\times$3の格子上に二人のプレイヤーが「o」「x」を配置し自分のマークを3つ並べるゲームである．

誰もが一度はやったことあるゲームだと思います．以下に実装した3目並べのプログラムを載せます

from enum import Enum, auto

# マスの状態
class BoardState(Enum):
    BLANK = auto()
    PLAYER = auto()
    AI = auto()
    
# ゲームの状態
class GameState(Enum):
    GAME = auto()
    PLAYER_WIN = 'PLAYER_WIN'
    AI_WIN = 'AI_WIN'
    DRAW = 'DRAW'

class Board():
    
    def __init__(self):
        # ボードの初期化
        self.board = [BoardState.BLANK for _ in range(9)]
        # 先攻後攻
        self.my_turn = True
        
        print('0|1|2\n-----\n3|4|5\n-----\n6|7|8\n')
                
        # ゲーム開始
        self.state = GameState.GAME
        while self.state == GameState.GAME:
            if self.my_turn:
                # 先攻
                self.player_input()
            else:
                # 後攻
                self.player_input()
            self.display_board()
        print(self.state)
        
    # ボードを表示する
    def display_board(self):
        tmp = []
        for i in range(9):
            if self.board[i] == BoardState.BLANK:
                tmp.append('  ')
            elif self.board[i] == BoardState.PLAYER:
                tmp.append('o')
            elif self.board[i] == BoardState.AI:
                tmp.append('x')
                
        print('{0[0]}|{0[1]}|{0[2]}\n'\
        '-----\n{0[3]}|{0[4]}|{0[5]}\n'\
        '-----\n{0[6]}|{0[7]}|{0[8]}\n'.format(tmp))
        
    # プレイヤーの入力
    def player_input(self):
        while True:
            try:
                value = int(input('please input value'))
                if self.can_put_value(value):
                    self.put_value(value)
                    break
                else:
                    print('do not put')
            except:
                print('attribute error')
    
    # ターンを交代する
    def change_turn(self):
        self.my_turn = not(self.my_turn)
        
    # valueがBLANKならTrue
    def can_put_value(self, value):
        return True if self.board[value] == BoardState.BLANK else False
    
    # valueに置く
    def put_value(self, value):
        self.board[value] = BoardState.PLAYER if self.my_turn else BoardState.AI
        self.check_state()
        self.change_turn()

    # 勝敗がついているならTrue
    def judge(self, a, b, c):
          return True if a == b == c and a != BoardState.BLANK else False
    
    # ゲームの状態を更新
    def check_state(self):
        for i in range(3):
            if self.judge(*self.board[i:9:3]) or self.judge(*self.board[3*i:3*i+3]) or self.judge(*self.board[0:9:4]) or self.judge(*self.board[2:7:2]):
                if self.my_turn:
                    self.state = GameState.PLAYER_WIN
                    return
                else:
                    self.state = GameState.AI_WIN
                    return
                
        if all(BoardState.BLANK != state for state in self.board):
            self.state = GameState.DRAW
            return
        
        self.state = GameState.GAME
        

これを実行することにより，対人での3目並べができます．
次からはミニマックス法を実装する上で必要となる知識についてです．

ゲーム木探索

まずはゲーム木について説明します．

ゲーム木

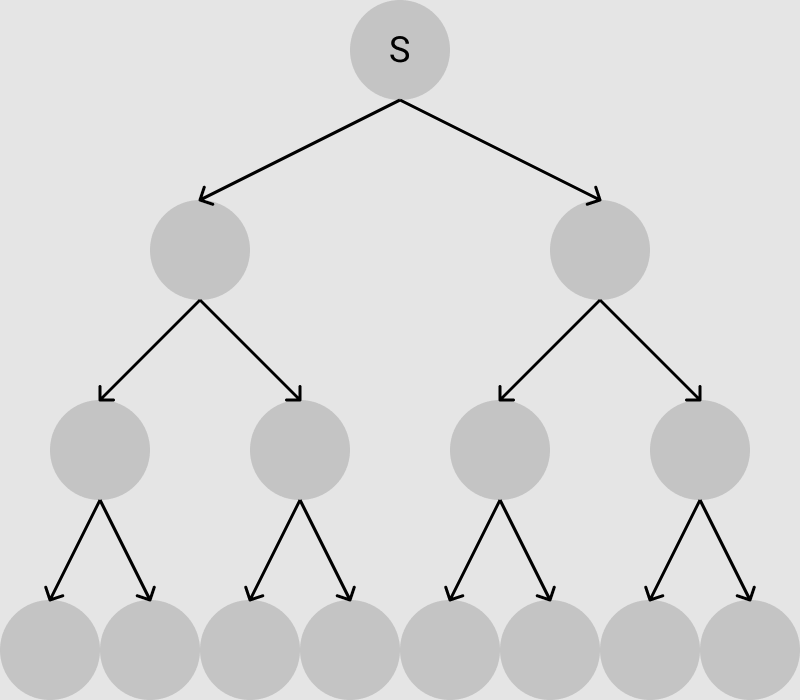
起こり得る全ての局面を樹形図にしたもの

図で表すと以下のようなイメージです．

現在の局面をSとして自分の取り得る行動をしたときに次の局面に移動します．

次にゲーム木探索とその周辺語句の説明をします．

ゲーム木探索

評価値が最大となる局面を探すこと

評価値

局面の形勢を数値で表したもの

評価関数

評価値を返す関数．探索をしてその局面の有利さを評価値として返す．

です．
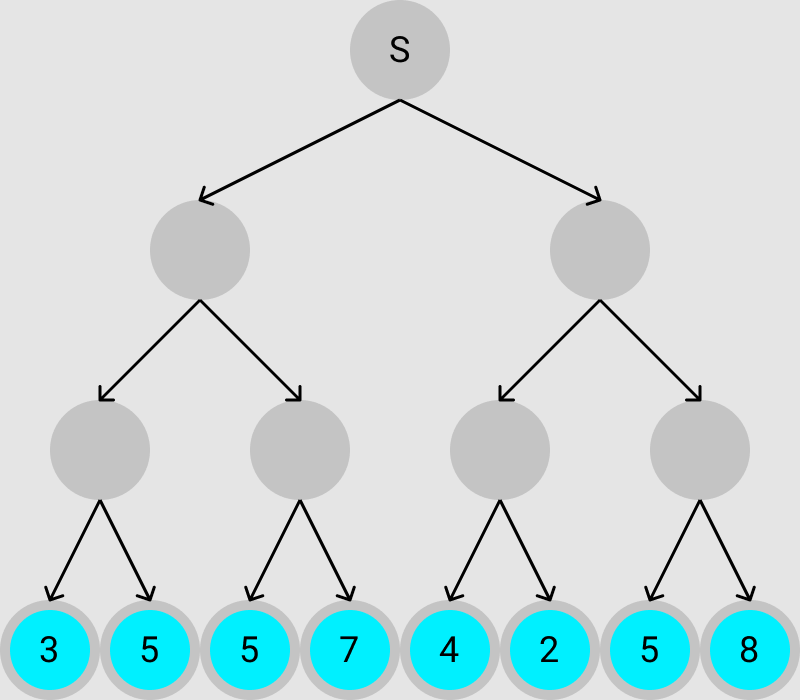
以下の図は，先程の図に評価値を追加した図になります．青い丸が評価関数を表していて，その中の数字が評価値です．

例えば，この場合だと，評価関数から得られた最大の評価値は「8」なので，現在の局面Sから評価値が「8」となる局面を探索しなければなりません．

ゲーム木を探索するには探索アルゴリズムを使用します．
今回は交互に手番を交代するゲームであり，探索範囲もそれほど大きくないので，ミニマックス法が適当です．

ミニマックス法

概要

次は本題のミニマックス法について説明をしていきます．

ミニマックス法

最も評価値が高くなる指し手を選択する手法である．
互いに最善な手を選択すると仮定して木を探索する．(自分の最善な指し手は，評価値が最も高い．相手の最善な指し手は，評価値が最も低いとする．)

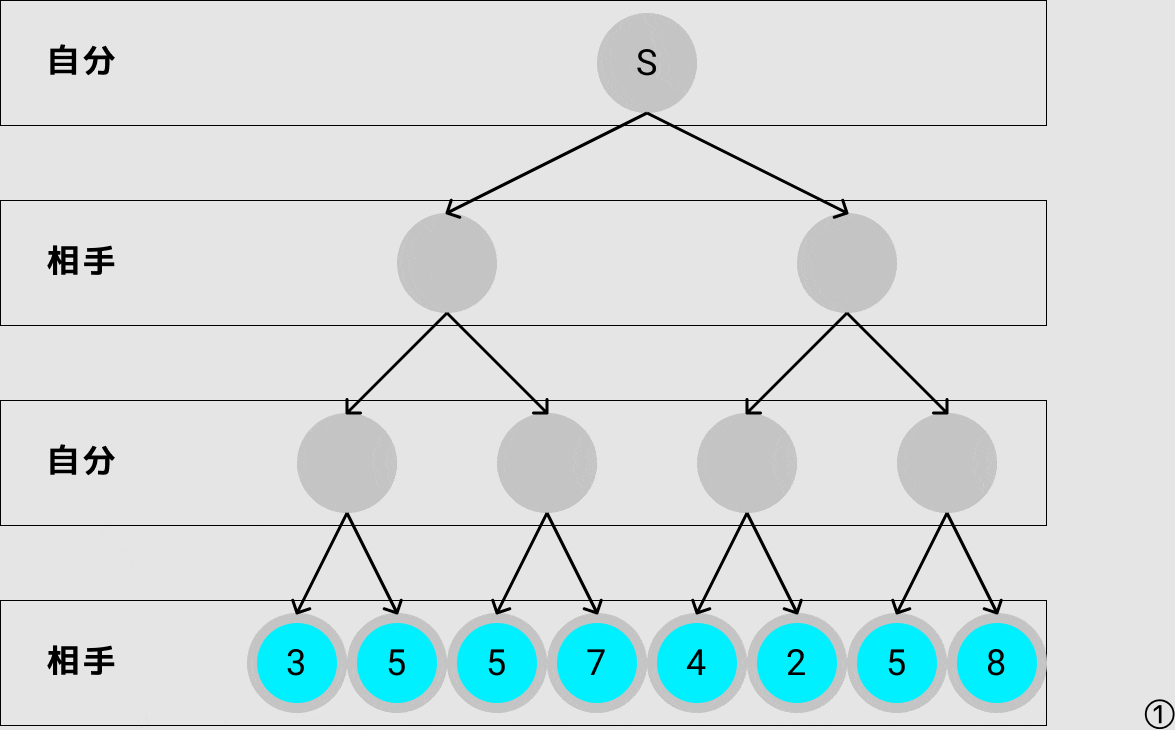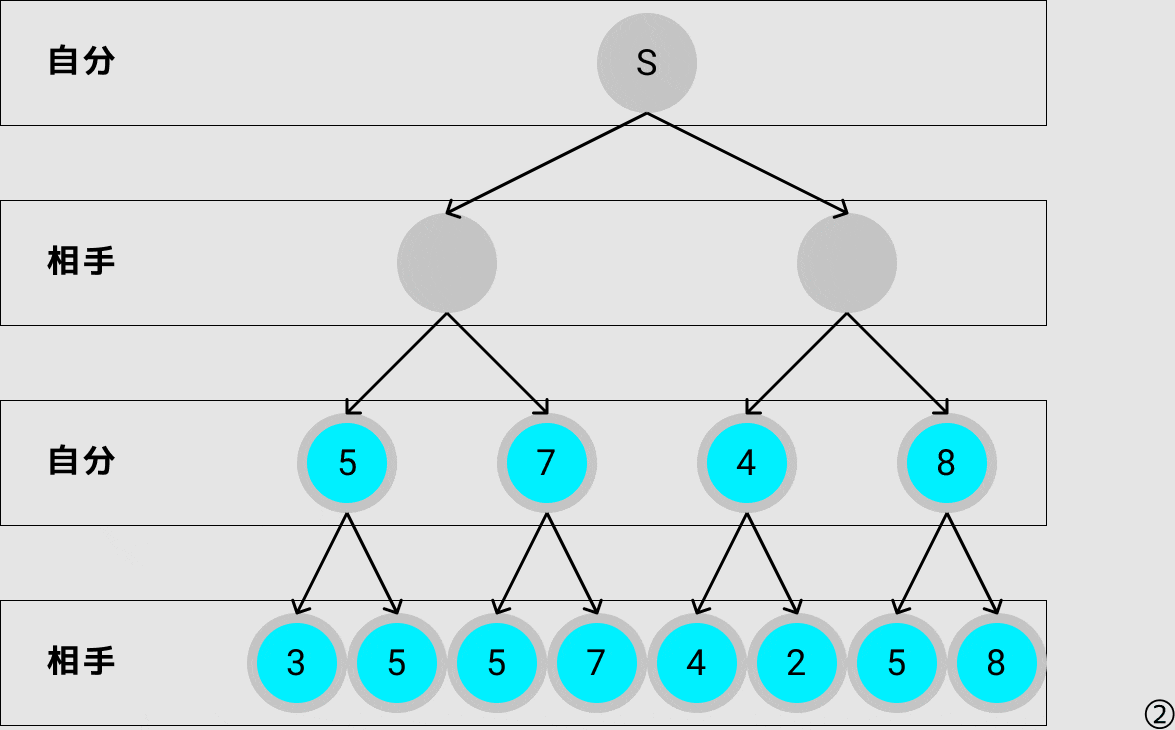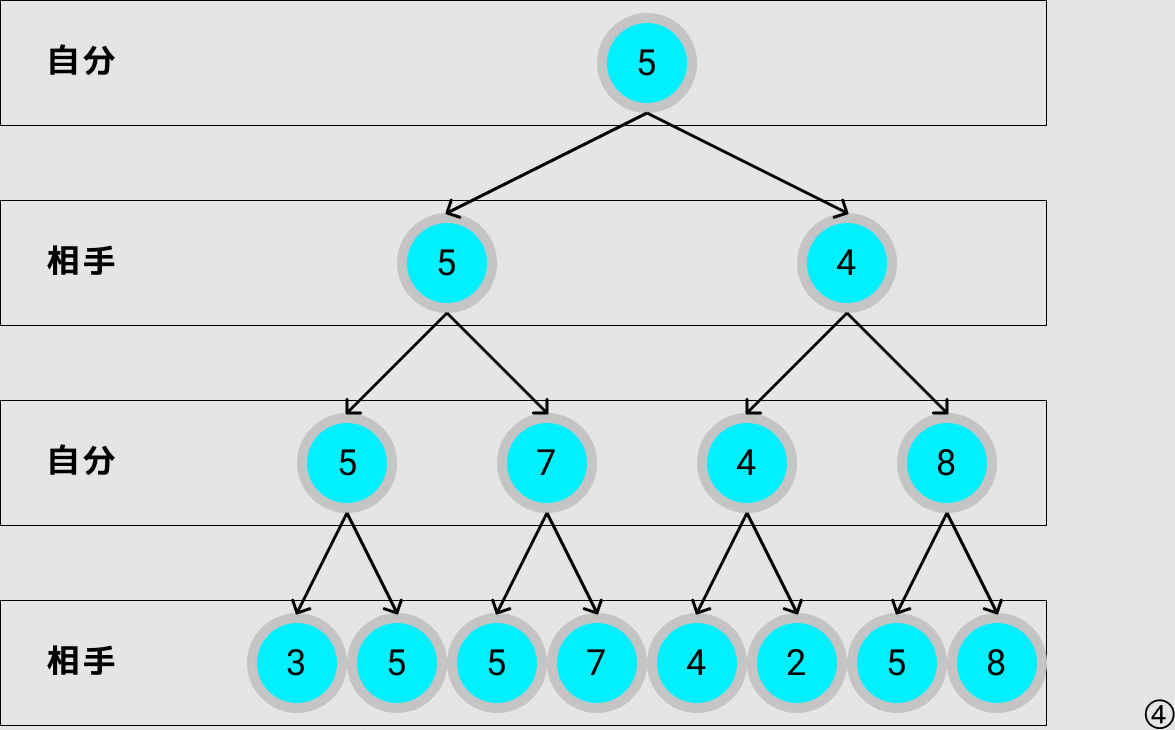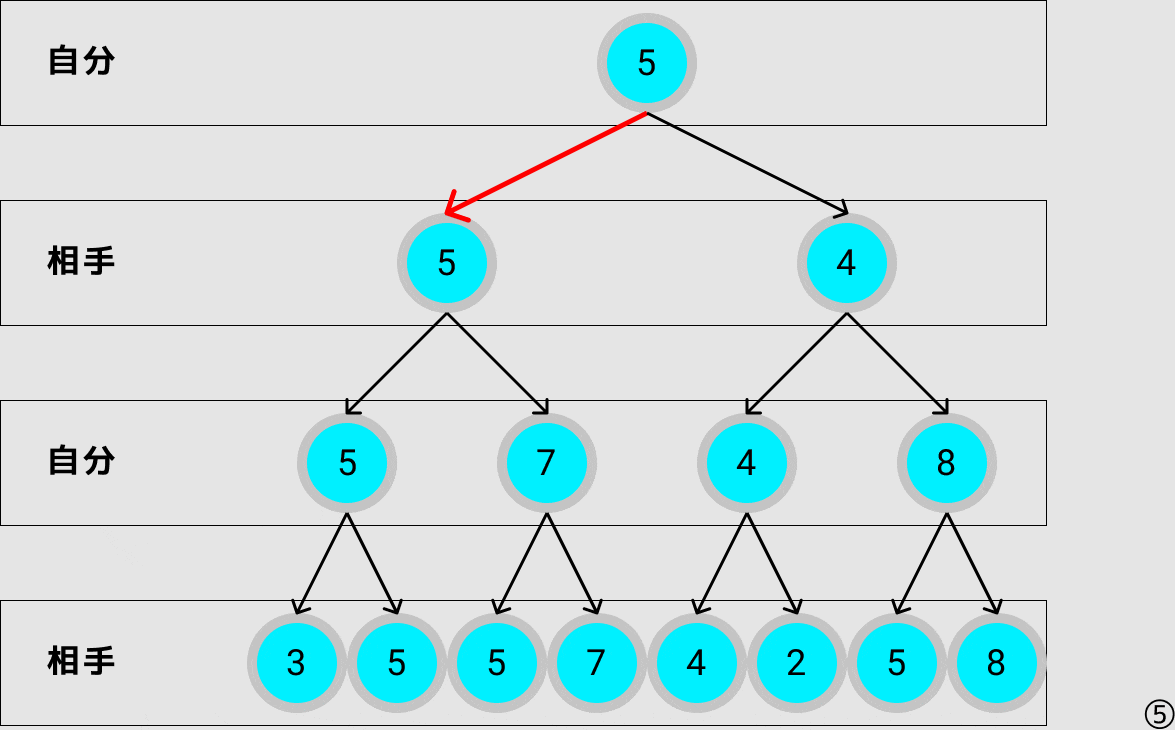
現在の局面Sは自分の番です．木のノードが下に行くに連れて，相手，自分，相手，...と手番が変わっていきます．

ミニマックス法のアルゴリズムは以下です．

1. 先読みする手番の全ノードの評価値を設定する
2. 自分の手番なら子ノードの評価値のうち最高値を取得
3. 相手の手番なら子ノードの評価値のうち最低値を取得
4. 開始ノードまで2，3を繰り返す
5. 開始ノードから評価値が最大のノードを最善の手として選択

次に自分が選ぶべき最善手をミニマックス法で探索すると上のgif画像の様になり，評価値が5となるノードに遷移します．

では，実際に3目並べにミニマックス法を実装して最強のAIを作ります．

プログラム

class Board():
    
    # ----- ３目並べプログラム ----- #


    # ----- ３目並べプログラム ----- #

    # valueを空にする
    def undo_value(self, value):
        self.board[value] = BoardState.BLANK
        self.change_turn()    
    
    # 次の手を考える
    def ai_think(self):
        print("AI")
        self.put_value(self.minimax(0))

    # ミニマックス法で探索
    def minimax(self, depth):
        if self.state != GameState.GAME:
            return self.evaluate(depth)
        
        best_value = 0
        value = 10000 if self.my_turn else -10000
        
        for i in range(9):
            if self.can_put_value(i):
                self.put_value(i)
                child_value = self.minimax(depth+1)
                if self.my_turn:
                    if child_value > value:
                        value = child_value
                        best_value = i
                else:
                    if child_value < value:
                        value = child_value
                        best_value = i
                self.undo_value(i)
        
        if depth == 0:
            return best_value
        else:
            return value
        
    # 評価関数
    def evaluate(self, depth):
        if self.state == GameState.AI_WIN:
            self.state = GameState.GAME
            return 10 - depth
        elif self.state == GameState.PLAYER_WIN:
            self.state = GameState.GAME
            return depth -10
        else:
            self.state = GameState.GAME
            return 0
        

評価関数では自分が勝つ局面なら10を，負ける局面なら-10を，引き分けの場合には0を返します．
また，勝つ場合には早くかつ局面を選択したほうが良いゲームになるため，10から探索した深さを引き，負ける場合にはできるだけ長引かせる局面を選択したほうが良いゲームになるため，-10に探索した深さを足します．

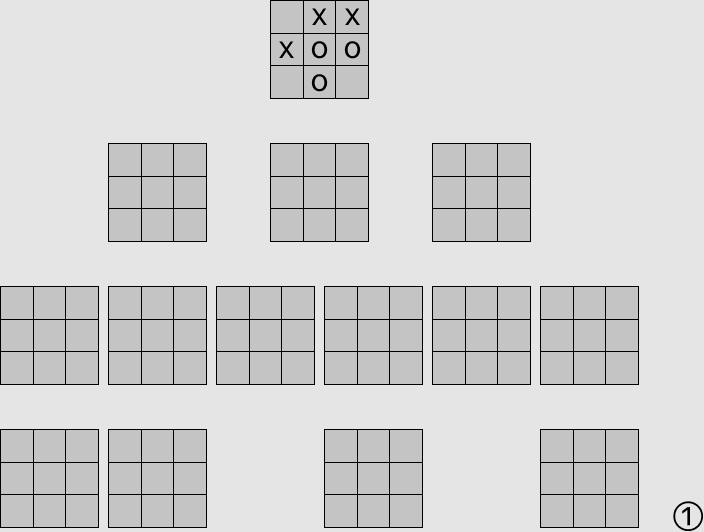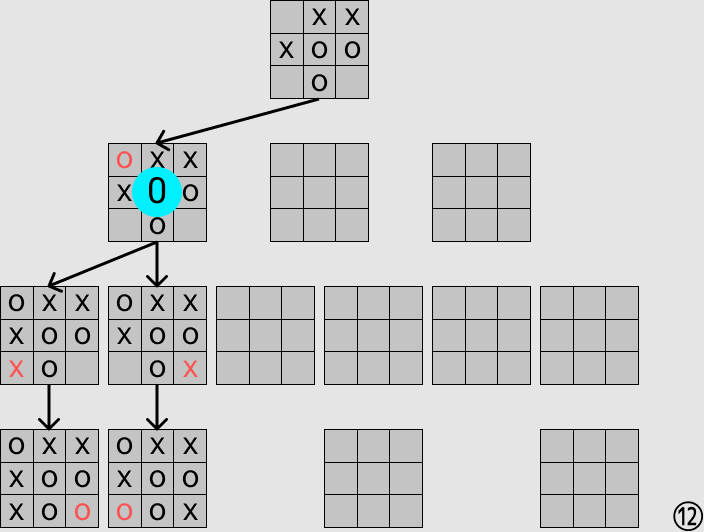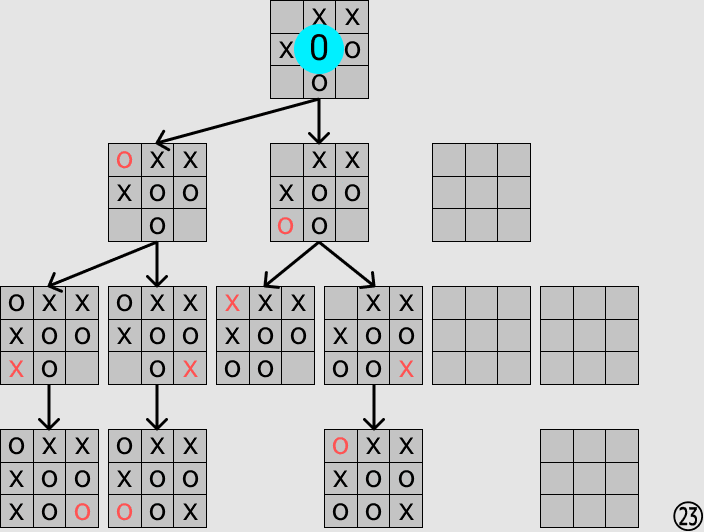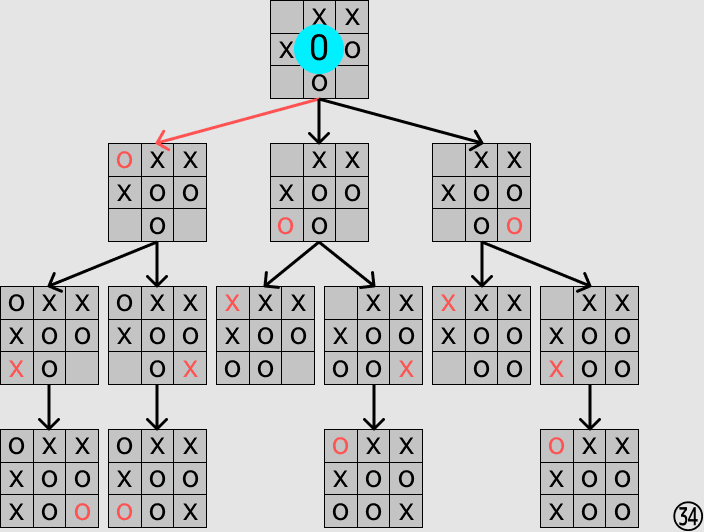
実際に探索している様子を可視化すると以下のようになります．

すべてのプログラムはこちらから

終わりに

今回は3目並べを題材にミニマックス法で最強のAIを実装しました．

ミニマックス法の拡張アルゴリズムであるアルファベータ法を実装することにより，メモリ的，計算時間的に余裕が出てリバーシなどのゲームAIも作成することができます．

最近流行りの"AI"だけではなく，古典的な"AI"の技術も学んでバチイケなプログラマになりましょう！

それでは，Happy Hacking!