前回、日本の古文書で機械学習を試す(4) LSTM(RNN)で次に来る文字を予測は失敗に終わったのだが、時系列処理のRNNをもう少し使ってみたいと思っていたところ、「詳解ディープラーニング」という本の第6章に、RNNを使ってMNIST(手書き文字判別)を行うアイディアが載っていたので早速試してみる。
今回使うのは、Bidirectional RNNというモデル。過去から未来だけでなく、未来から過去へのフィードバックも利用するというもので、既にあるデータから未来を予測するという一般的な「予測」には使えないが、録音済みの音声や、完結したテキストなど、時系列の一連のデータが既にある場合に使うらしい。
日本の古文書で機械学習を試す(1)で使った28×28ピクセルの画像の、縦方向を時間軸ととらえて、RNNモデルへの入力とする。縦に流れるドット式の電光掲示板の1行に着目するようなイメージだろうか。28ドット×時間ステップ28個分を入力として、10個の要素のうち1個だけが1になるベクトルを出力(0~9のうちどの番号の文字かを判別する)モデルを構築する。
データ生成、モデル定義
基本的には、日本の古文書で機械学習を試す(1)と同じサンプルプログラムのデータを使う。サンプルプログラムで生成した学習用データ、テストデータを、RNNの入力に合うように変換する。
# 学習、テスト用の入力データの次元数を減らす。
# img_rowsの次元を時間の次元として扱う(1行目=時間ステップ1、2行目=時間ステップ2のように、上から下に時間が流れる)
print('X_train shape before:', X_train.shape)
X_train = X_train.reshape(len(X_train), img_rows, img_cols)
X_test = X_test.reshape(len(X_test), img_rows, img_cols)
print('X_train shape after:', X_train.shape)
変換前と変換後の学習用データのデータ型を表示してみるとこうなっている。
X_train shape before: (19909, 28, 28, 1)
X_train shape after: (19909, 28, 28)
次にモデルを定義する。最適化関数とパラメータはとりあえず「詳解ディープラーニング」に載っていたものを使う。
from keras.models import Sequential
from keras.layers.wrappers import Bidirectional
from keras.layers import Dense, Activation, LSTM
from keras.optimizers import Adam
n_hidden = 128 # 隠れ層の次元数
model = Sequential()
model.add(Bidirectional(LSTM(n_hidden), input_shape=(img_rows, img_cols)))
model.add(Dense(nb_classes))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=0.001, beta_1=0.9, beta_2=0.999), metrics=['accuracy'])
学習させてみる
何も考えずにとりあえず走らせてみる。エポック数300、バッチサイズ128は「詳解ディープラーニング」に載っていたもの。
# 学習
result = model.fit(X_train, Y_train, batch_size=128, epochs=300, verbose=1, validation_data=(X_test, Y_test))
# テストデータに対して信頼度を表示
score = model.evaluate(X_test, Y_test, verbose=1)
print('Test score:', score[0])
print('Test accuracy:', score[1])
学習時間は1エポックあたり30秒弱、約2時間で結果が表示された。
Test score: 0.3494065668820907
Test accuracy: 0.9544678429479821
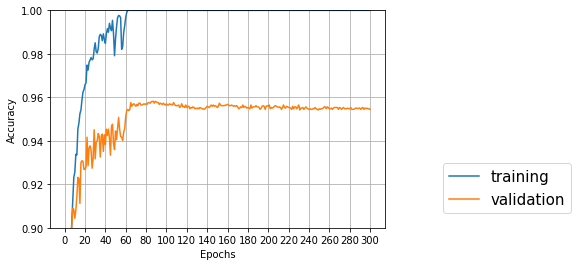
パラメーターチューニングする前のサンプルプログラム(CNN)よりちょっと高い正解率が出た。前回までと同じように学習結果をプロットするコードを書いて表示させてみた。
# result.historyに保存された学習データとテストデータに対する正解率をプロット
import matplotlib.pyplot as plt
%matplotlib inline
epochs = 300
plt.plot(range(1, epochs+1), result.history['acc'], label="training") # 学習データ
plt.plot(range(1, epochs+1), result.history['val_acc'], label="validation") # テストデータ
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim([0.9,1])# y軸の最小値、最大値
plt.grid(True) # グリッドを表示
plt.xticks(np.arange(0, epochs+1, 10))
plt.legend(bbox_to_anchor=(1.6, 0), loc='lower right', borderaxespad=1, fontsize=15)
plt.show()
これを見ると、テストデータの正解率ピークは60~90エポックぐらいで、その先は過学習でちょっとずつ正解率が下がっている。300エポックは多すぎるらしい。
パラメータ調整
バッチサイズと隠れ層のサイズを変えて、正解率がどのように変わるか試してみる。
その前に、正解率が一番高かったエポックのモデルを保存できるように、ModelCheckpointを使って学習時に用いるコールバック関数を定義した。
from keras.callbacks import ModelCheckpoint
import os
model_checkpoint = ModelCheckpoint(
# 保存するモデル名にエポック数とテストデータの正解率を含める
filepath=os.path.join('rnn_mnist_models','model_komonjo_rnn_mnist_{epoch:02d}_{val_acc:.3f}.h5'),
monitor='val_acc', # 監視するパラメータはテストデータの正解率
mode='max', # 正解率を最大化したい
save_best_only=True, # 前回よりval_accが良い時だけ保存
verbose=1)
学習時にcallbacksとして生成した関数を渡す。
result = model.fit(X_train, Y_train, batch_size=32, epochs=70, verbose=1, validation_data=(X_test, Y_test),
callbacks=[model_checkpoint])
これで、(スクリプトがあるフォルダ)/rnn_mnist_models/のフォルダに、
model_komonjo_rnn_mnist_61_0.975.h5
のようなファイルが保存されていく。
エポック数を70に設定して、バッチサイズと隠れ層のサイズを変えてみた結果は以下の通り。
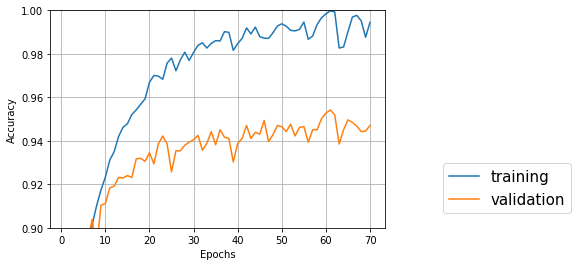
↑バッチサイズ128、隠れ層128、エポック70
Test accuracy: 0.9470688673875924
一番良いのは61エポック目でval_acc: 0.9542
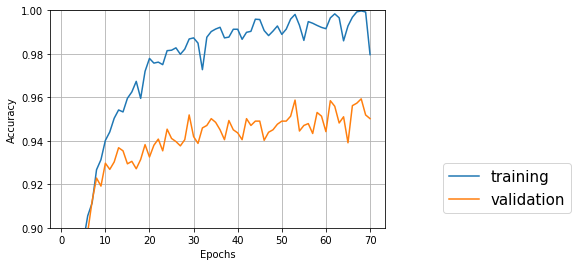
↑バッチサイズ64、隠れ層128、エポック70
Test accuracy: 0.9501992032211751
一番良いのは68エポック目でval_acc: 0.9593
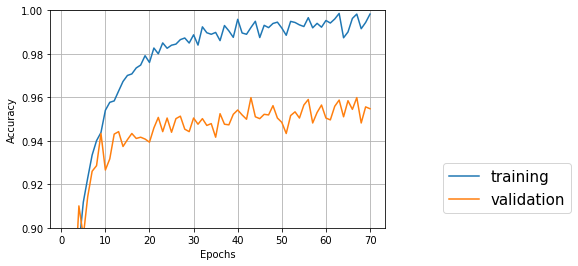
↑バッチサイズ32、隠れ層128、エポック70
Test accuracy: 0.9547524188958452
一番良いのは43エポック目でval_acc: 0.9599
バッチサイズが小さい方が正解率が少しだけ高くなり、学習も早く進んでいるようだが、劇的な効果はなさそう。
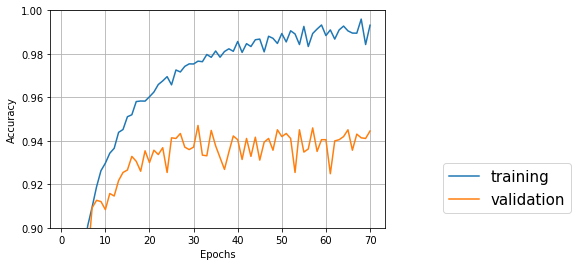
↑バッチサイズ32、隠れ層64、エポック70
Test accuracy: 0.9445076835515083
一番良いのは31エポック目でval_acc: 0.9471
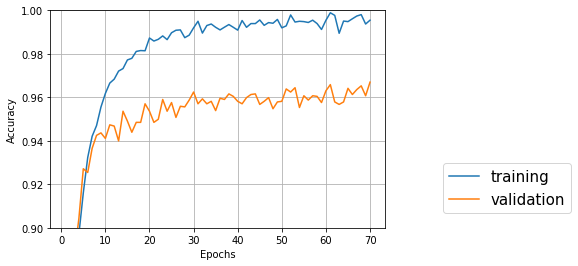
↑バッチサイズ32、隠れ層256、エポック70
Test accuracy: 0.9669891861126921
一番良いのは70エポック目
隠れ層のサイズは、256のほうが128、64よりも正解率が良くなった。しかし、隠れ層サイズ128では1エポック当たりの所要時間が30秒弱だったのに対し、256では200秒前後とかなり遅くなってしまった。グラフを見ると、エポックを増やすともう少し良くなるような気がしたので、追加学習させてみた。
モデル定義のかわりに、保存したモデルを読み込んで、同じように学習させる。追加で100エポック学習させてみた。
# 保存したモデルを読み込む
from keras.models import load_model
model = load_model('rnn_mnist_models/model_komonjo_rnn_mnist_epoch70_batch32_hidden256_70_0.967.h5')
# 学習
result = model.fit(X_train, Y_train, batch_size=32, epochs=100, verbose=1, validation_data=(X_test, Y_test),
callbacks=[model_checkpoint])
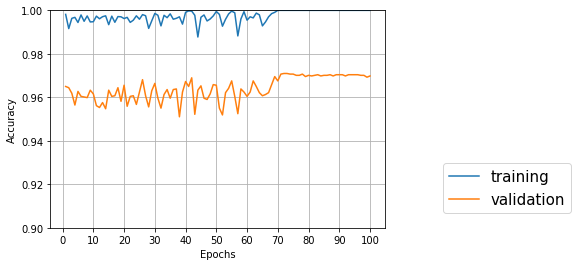
↑バッチサイズ32、隠れ層256、エポック70+100
Test accuracy: 0.9698349459305634
一番良いのは72エポック目でval_acc: 0.9707
70エポック学習済みのモデルを読み込んでスタートしたので、最初から高い正解率が出ている。しばらくギザギザした後+70エポックぐらいで収束している。トータルで140エポックぐらい必要なのだろうが、時間がかかる…
CNNと比較
隠れ層サイズ256は時間がかかりすぎるので、バッチサイズ32、隠れ層128、エポック70のパラメータを採用したとして、正解率0.9599は日本の古文書で機械学習を試す(3) で、CNNのパラメータをチューニングした結果より良さそうに見える。
しかし、以前にCNNで試したときはエポック数12で止めていたので、RNNと同じバッチサイズ32、エポック70、最適化関数Adamで再度試してみる。こちらもコールバックを設定して一番良かったエポックのモデルを保存する。
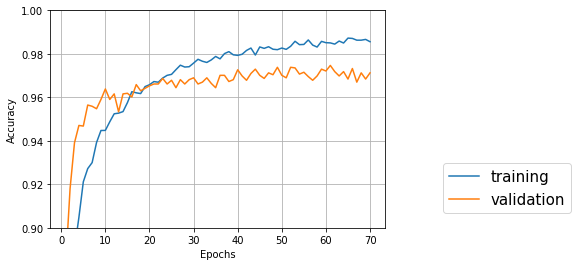
↑バッチサイズ32、エポック70、CNN
Test accuracy: 0.9712578258394992
一番良いのは61エポック目でval_acc: 0.9747
やはりエポック12以降も徐々に正解率が上がっていて、RNNより良い結果となった。画像認識にはCNNが適しているというのは、嘘ではないらしい。
縦横を逆にしてみる
次に、ベクトル方向と時間方向を入れ替えてみる。縦に流れる電光掲示板から横に流れる電光掲示板に変更するイメージで。
ソースコード的にはシンプルで、学習前に画像の縦横を入れ替えるだけ。本当はmodelのinput_shape=(img_rows, img_cols)も逆にする必要があるが、今回はどちらも28なのでそのままにしておく。
隠れ層のサイズは256のほうが精度は良いが、時間がかかるので今回は128で試す。
# 画像データの縦と横を入れ替える、1列目=時間ステップ1、2列名=時間ステップ2のように、左から右に時間が流れる
X_train = X_train.transpose(0, 2, 1)
X_test = X_test.transpose(0, 2, 1)
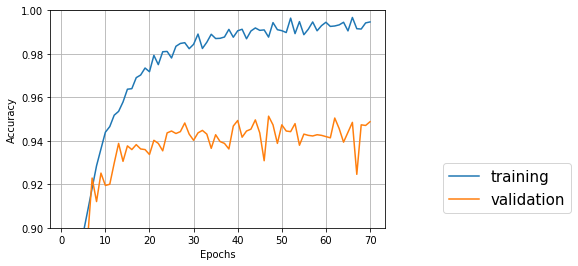
↑バッチサイズ32、隠れ層128、エポック70、縦横入れ替え
Test accuracy: 0.9487763232783153
一番良いのは47エポック目でval_acc: 0.9513
入れ替え前より少し精度が落ちているが、誤差範囲かもしれない。
それぞれ、どの文字で認識に失敗しているのかをチェックしてみる。
# 認識に失敗したデータをチェック
miss_count= [0] * 10
count= 0
for i, x in enumerate(X_test):
# 正解データ
correct_index = np.where(Y_test[i] == True)[0][0] # データがTrueになっている箇所のインデックス
## どの文字かを判別する
x = np.array([x])
preds = model.predict(x)
pred_index = preds.argmax() # 確率の一番高い文字の番号
# 間違っているものを表示
if correct_index != pred_index:
miss_count[correct_index] = miss_count[correct_index] + 1
print(i, " 正解=", correct_index, " 判別結果", pred_index)
count = count + 1
for i, c in enumerate(miss_count):
print(i , " " , c , "回")
print("間違い個数", count, "/", len(X_test))
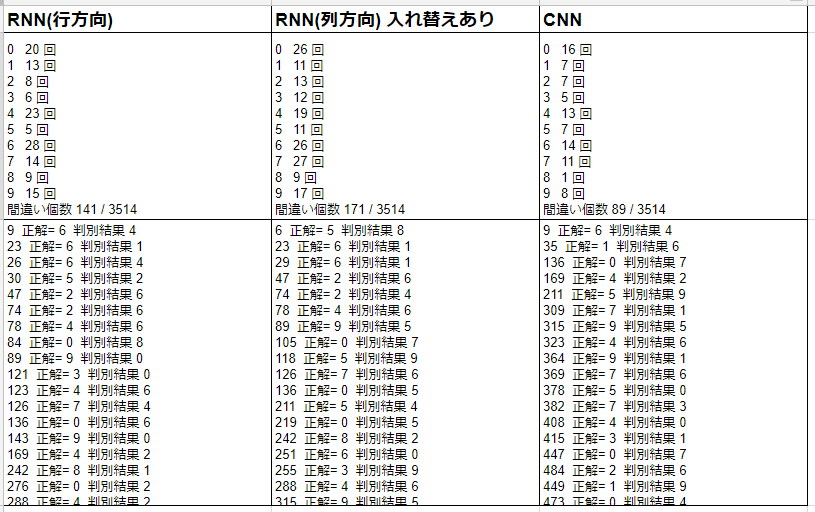
出力結果を比較しやすいようにスプレッドシートに貼り付けてみた。各番号に対応する文字は、0[し]、1[に]、2[の]、3[て]、4[り]、5[を]、6[か]、7[く]、8[き]、9[も]。
どのモデルでも、0[し]、4[り]、6[か]あたりが間違えやすいようだが、統計結果を見ても、個別の間違いを見ても、少しずつ傾向が異なっている。
3つのモデルですべて間違えていた文字をいくつか表示させてみた。
import matplotlib.pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(8,5)) # 全体の表示領域のサイズ(横, 縦)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.5, wspace=0.05)
# ↑サブ画像余白(左と下は0、右と上は1で余白なし) サブ画像間隔 縦,横
for i,c in enumerate([136, 315, 408, 473, 550]):
ax = fig.add_subplot(5, 8, i + 1, xticks=[], yticks=[]) # 縦分割数、横分割数、何番目か、メモリ表示なし
# 画像番号と正解の番号を表示
ax.title.set_text("[" + str(c) + "]," + str(np.where(Y_test[c] == True)[0][0]))
ax.imshow(X_test[c].reshape((img_rows, img_cols)), cmap='gray')

正解は左から「し」「も」「り」「し」「か」。これは難易度高すぎでは(汗)
モデルを組み合わせる
上の結果から、モデルごとに間違いの傾向が違っていたので、組み合わせてみると精度が上がるのではないかと考え、試してみた。日本の古文書で機械学習を試す(1)と同様にして、テスト用データは既に読み込み済みの前提で、RNN用にデータを変換した後、バッチサイズ32、エポック70のRNN行方向(縦横入れ替えなし)、RNN列方向(縦横入れ替えあり)、CNNの、一番精度が良かったモデルを読み込む。
それぞれのモデルに対して、予測結果のベクトル(文字0~9に対する各確率をあらわしたベクトル)を求め、3つのモデルの結果を加算する。加算方法としては、
・単純に3つのモデル分を加算して、正規化のため(確率が0~1の間になるように)3で割る
・CNN1種類、RNN2種類なので、CNNとRNNの重みが同等になるように、RNN2種類に0.5をかけてから加算して、正規化のため2で割る
・CNNのほうが精度が良いので重みを2倍にして、正規化のため3で割る
の3種類で試してみる。同じベクトル内で確率が最大のものを求めるだけなので、正規化しなくても結果は変わらないが、後で別のことに使いたくなるかもしれないので、いちおう正規化しておく。
# RNN用にデータ形式を変換
X_test_RNN_Row = X_test.reshape(len(X_test), img_rows, img_cols)
X_test_RNN_Col = X_test_RNN_Row.transpose(0, 2, 1)
# CNN、RNNのモデル読み込み
from keras.models import load_model
model_cnn = load_model('rnn_mnist_models/model_komonjo_mnist_again_epoch70_batch32_adam_61_0.975.h5')
model_rnn_row = load_model('rnn_mnist_models/model_komonjo_rnn_mnist_epoch70_batch32_43_0.960.h5')
model_rnn_col = load_model('rnn_mnist_models/model_komonjo_rnn_mnist_Col_epoch70_batch32_47_0.951.h5')
# CNNとRNNを組み合わせて精度チェック
miss_count1 = 0
miss_count2 = 0
miss_count3 = 0
for i, x in enumerate(X_test):
# 正解データ
correct_index = np.where(Y_test[i] == True)[0][0] # データがTrueになっている箇所のインデックス
# 各モデルで判別結果のベクトルを求める
preds_cnn = model_cnn.predict(np.array([x]))
preds_rnn_row = model_rnn_row.predict(np.array([X_test_RNN_Row[i]]))
preds_rnn_col = model_rnn_col.predict(np.array([X_test_RNN_Col[i]]))
# ベクトルを加算
preds1 = (preds_cnn + preds_rnn_row + preds_rnn_col) / 3 # 単純加算、いちおう正規化のため3で割る
preds2 = (preds_cnn + preds_rnn_row*0.5 + preds_rnn_col*0.5) / 2 # RNNは2つあるので重みを半分に
preds3 = (preds_cnn*2 + preds_rnn_row*0.5 + preds_rnn_col*0.5) / 3 # CNNのほうが精度がいいので重みを大きめに
## どの文字かを判別する
pred_index1 = preds1.argmax() # 確率の一番高い文字の番号
pred_index2 = preds2.argmax()
pred_index3 = preds3.argmax()
# 間違っている場合にインクリメント
if pred_index1 != correct_index:
miss_count1 = miss_count1 + 1
if pred_index2 != correct_index:
miss_count2 = miss_count2 + 1
if pred_index3 != correct_index:
miss_count3 = miss_count3 + 1
print("正解率1 ", 1-miss_count1/len(X_test))
print("正解率2 ", 1-miss_count2/len(X_test))
print("正解率3 ", 1-miss_count3/len(X_test))
結果はこうなった。CNN単体、RNN単体よりも精度がアップしている!各モデルに対する重みも、機械学習で求めるとさらに良くなるかもしれないが、やり方がすぐに分からないので今回はやめておく。
正解率1 0.9803642572566875
正解率2 0.981217985202049
正解率3 0.9775184974388161