前々回、日本の古文書で機械学習を試す(1)で作成したモデルのパラメーターチューニングをしてみる。
機械学習の精度向上には、ニューラルネットワークの層を最適化するのが一番効きそうな気がするが、畳み込みとかMaxPoolingとか、まだよく理解できてないので、今回は最適化関数と、学習時のバッチサイズ、学習率をチューニングしてみた。
最適化関数を変更してみる
最適化関数とは、学習用データの入力値からモデルを使って計算した結果と、学習用データの出力値(正解データ)の差分から、モデルをどうやって更新するかを定義した関数のこと(と初心者的には理解した。)
最適化関数は、元のサンプルコードのrun.pyの64行目あたり、compile関数の引数optimizerとして定義されている。サンプルでは「adadelta」が選択されている。
model.compile(loss='categorical_crossentropy',
optimizer='adadelta',
metrics=['accuracy'])
Kerasで使える最適化関数は、Kerasのマニュアルに書いてあったので、これを全部試してみることにする。サンプルプログラムのモデル定義~学習部分を以下のように書き換える。
# 使用する最適化関数の名前リスト
opt_list = ["adadelta", "adam", "adamax", "nadam", "adagrad", "sgd", "rmsprop"]
# 各最適化関数の学習結果を格納する変数を定義
results = [0] * len(opt_list) # opt_listと同じ長さの配列を確保
# 各最適化関数のモデルを格納する変数を定義
models = [0] * len(opt_list)
# 複数の最適化関数についてループ
for i in range(len(opt_list)):
np.random.seed(1337) # for reproducibility # 元のサンプルコードのまま
# 【モデル定義】基本的に元のサンプルコードのまま
models[i] = Sequential()
models[i].add(Conv2D(nb_filters, kernel_size,
padding='valid',
input_shape=input_shape))
models[i].add(Activation('relu'))
models[i].add(Conv2D(nb_filters, kernel_size))
models[i].add(Activation('relu'))
models[i].add(MaxPooling2D(pool_size=pool_size))
models[i].add(Dropout(0.25))
models[i].add(Flatten())
models[i].add(Dense(128))
models[i].add(Activation('relu'))
models[i].add(Dropout(0.5))
models[i].add(Dense(nb_classes))
models[i].add(Activation('softmax'))
models[i].compile(loss='categorical_crossentropy',
optimizer=opt_list[i], ### ここを変更
metrics=['accuracy'])
# 【学習】元のサンプルコードのまま
results[i] = models[i].fit(X_train, Y_train, batch_size=batch_size,
epochs=nb_epoch, verbose=1,
validation_data=(X_test, Y_test))
# 【テストデータに対して信頼度を表示】
score = models[i].evaluate(X_test, Y_test, verbose=0)
print(opt_list[i], ' Test score:', score[0])
print(opt_list[i], ' Test accura
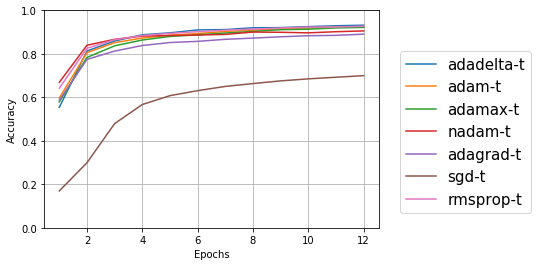
ついでに、学習結果をmatplotlibで可視化する。横軸にエポック(学習回数)、縦軸に正解率をプロットする。
import matplotlib.pyplot as plt
%matplotlib inline
for i in range(len(opt_list)):
# 学習データ
plt.plot(range(1, nb_epoch+1), results[i].history['acc'], label=opt_list[i]+"-t")
# テストデータ
#plt.plot(range(1, nb_epoch+1), results[i].history['val_acc'], label=opt_list[i]+"-v")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim([0,1])# y軸の最小値、最大値
plt.grid(True) # グリッドを表示
plt.legend(bbox_to_anchor=(1.5, 0), loc='lower right', borderaxespad=1, fontsize=15)
plt.show()
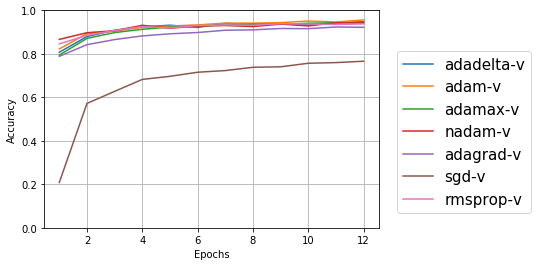
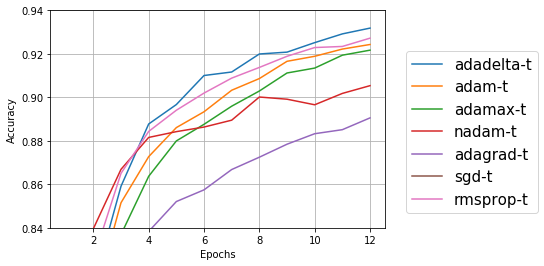
SGDがとても低いのは分かるが、ほかはゴチャゴチャでよくわからないので、y軸の最小値、最大値を変更して再度プロット。余談だが、学習用データ=trainigでt、テストデータ=validationでvの記号をふったら、テストデータ=tだっけ?とか混乱してしまった(笑)
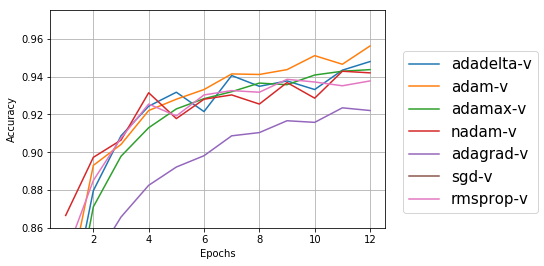
学習用データについては、元々のadadeltaのほうが精度が良いが、テストデータについては、adamのほうが良い結果になっている。学習用データの精度だけが高いと過学習になっている可能性もあるので、この場合はテストデータの精度が高いadamのほうが良さそうな気がする。
精度が高いと言っても1%ぐらいなので、誤差の範囲かも?と思い、同じプログラムを5回ぐらい走らせてみたところ、sgdが極端に低く、次にadagradが低いのは変わらないが、精度の順位が結構変わり、数値も92%~95%とかなり変動する。np.random.seed()で、numpyの乱数の種を固定しても毎回違う数値が出るのは、numpyでない乱数も使われているのか?Kerasの中の話なので、今回は深追いするのはやめておく。KerasのFAQに「再現可能な結果を得るには?」というのがあったので、今度試してみよう。
エポックを増やしてみる
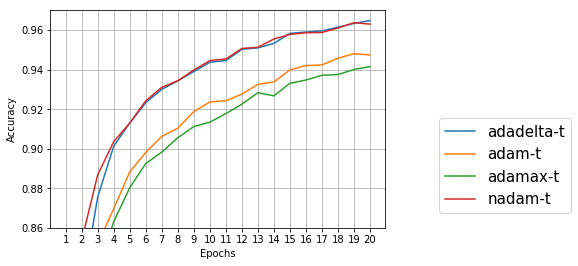
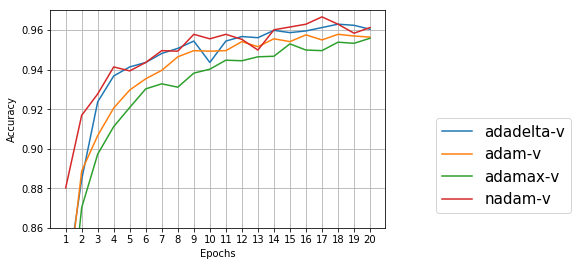
縦軸(精度)が0~1のグラフだとエポックを増やしてもあまり変わらないように見えるが、拡大グラフだとエポックを増やせばもう少し精度が上がりそうな気もするので、エポック20まで試してみた。
プロット時に横軸が0.5刻みになって気持ち悪かったので、以下の1行を追加した。
plt.xticks(np.arange(1, 21, 1))
学習用データだけでなく、テストデータもエポック12~20の間で精度が上がっている。今回はadadeltaとnadamが良さそうだが、テストデータでは誤差範囲かもしれない。もう少しエポック数を増やしてみたい気もするが、学習に時間がかかるのでこのあたりでやめておく。
バッチサイズを変更してみる
バッチサイズとはミニバッチ学習法で使うパラメータのこと。ミニバッチ学習法とは、全学習データを複数のバッチに分けて、バッチごとに誤差関数を計算してモデルを更新する方法のこと。全学習データ分の誤差関数を計算してからモデルを更新するのがバッチ学習法、学習データ1個の誤差関数を計算するごとにモデルを更新するのがオンライン学習法で、ミニバッチはその中間。
たとえば、19909個の学習用データで、ミニバッチサイズ128だと、1エポック当たり、19909/128 = 155回のモデル更新が行われる。端数のデータは学習には使われないが、エポックごとに学習用データがシャッフルされてバッチに分割されるので、エポックを増やせば全データが使われる可能性が高くなる。ちなみに、データのシャッフルの有無はmodel.fitのパラメータshuffleで定義するが、デフォルトがTrueなので、明記していないことが多いようだ。
最適化関数をadamに固定して、バッチサイズを変更してみる。元のサンプルプログラムのバッチサイズは128なので、1~256の間の数値で試してみる。最初の変数定義と、モデルのコンパイル、学習部分を少し変更する。
batch_sizes = [1, 8, 16, 32, 64, 128, 256]
results = [0] * len(batch_sizes)
models = [0] * len(batch_sizes)
(省略)
for i in range(len(batch_sizes)):
(省略)
models[i].compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
results[i] = models[i].fit(X_train, Y_train,
batch_size=batch_sizes[i], epochs=nb_epoch,
verbose=1, validation_data=(X_test, Y_test))
(省略)
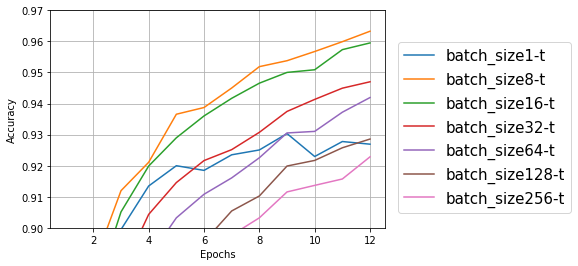
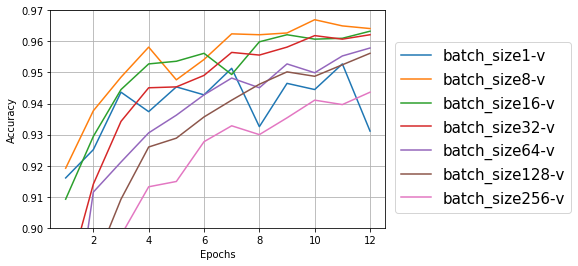
結果をプロットすると次のようになった。
テストデータも学習データも、バッチサイズ8、16、32あたりが良さそうな感じ。大きすぎても小さすぎてもダメっぽい。
バッチサイズが大きくなると学習時間がだんだん短くなり、私の環境ではバッチサイズ1では1エポックあたり300~400秒、バッチサイズ256では50-55秒だった。速くなるのはモデル更新の回数が減るためだろうか。
学習率を変更してみる
学習率とは、最適化関数を使ってモデルを更新するときに、1回にどのぐらいの幅で更新するかということ。最適化関数をadam、バッチサイズを8に固定して、学習率を変更してみる。
元のサンプルプログラムではデフォルト(lr=0.001)を使っていたので、その前後で変更してみる。
学習率は最適化関数の引数として定義するので、compileの引数optimizerを、最適化関数名ではなく、最適化関数のオブジェクトで渡すようにした。
lr_list = [1e-5, 1e-4, 0.001, 0.01, 0.1]
results = [0] * len(lr_list)
models = [0] * len(lr_list)
(省略)
for i in range(len(lr_list)):
(省略)
models[i].compile(loss='categorical_crossentropy',
optimizer=optimizers.Adam(lr=lr_list[i]),
metrics=['accuracy'])
(省略)
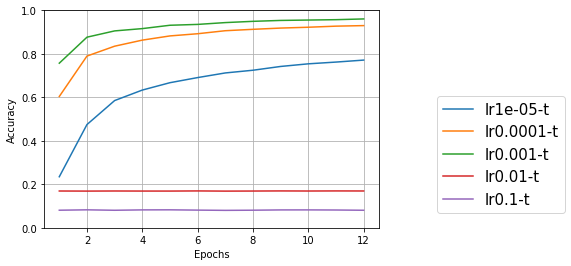
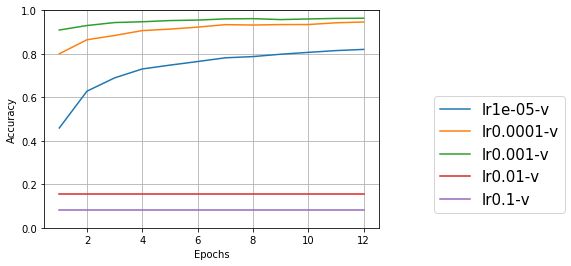
結果をプロットすると次のようになった。
今回試した範囲では、デフォルトの0.001が一番良さそうだ。1桁ずつの変更ではなく、もう少し細かく見ていけばもっと良い値があるのかもしれないが、デフォルトパラメータはそれなりに考慮された値なのだろう。