前回までの文字認識から少し離れて、古文書のデータをLSTM(RNN)を使って文字列を学習させ、文字列を入力したら次に来る文字を予測するというモデルを作ってみる。文字を入力する際の予測変換とちょっと近い処理かな?
データをダウンロード
前回までのサンプルプログラムと同じ人文学オープンデータ共同利用センターの日本古典籍くずし字データセットから、一番上の「好色一代男」をクリックして、一番上の「日本古典籍くずし字データの一括ダウンロード」から200003076.zipをダウンロード。サイトには文字種1720、文字数63959が含まれると書いてある。
解凍したフォルダの中身は以下の通り
- characters:1文字ごとに切り出した画像データが格納されているフォルダ(文字コード別にフォルダ分けされている)
- images:元の本の1ページごとの画像データが格納されているフォルダ
- 200003076_coordinate.csv:文字座標データ、詳細は後で解説する
- 200003076_report.csv:作業報告文書(データ作成時に読めなかった文字の情報や注意事項が書かれている)
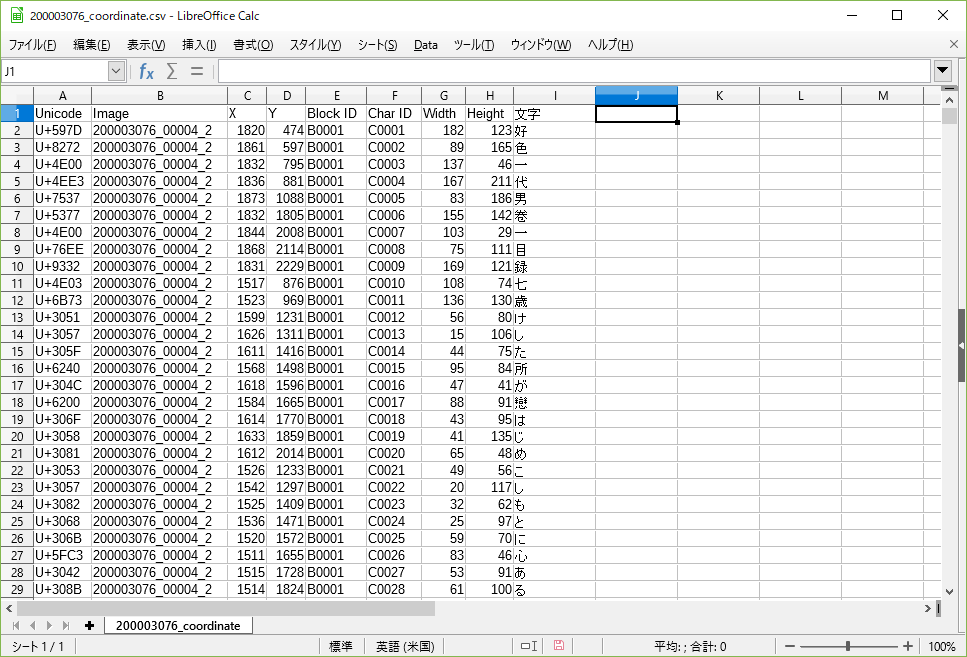
今回は、200003076_coordinate.csvのファイルのみを使う。ファイルの中身はこうなっている。
Imageはimagesに入っているページごとのデータのファイル名、X、Yはファイル上の文字の座標、BlockIDはファイル内(ページ内)のブロック番号(今回のデータは段組みがないので全部「B0001」が入っているが、段組みのあるページの場合は違うのだろう)、CharIDはファイル内(ページ内)での文字番号、WidthとHeightは文字のサイズを表している。
一番右の文字は私が追加した列で、セルに=UNICHAR(HEX2DEC(RIGHT([一番左のセル番号],4)))の式を入れた。一番左の列のUnicodeの左側4文字を16進数から10進数に変換した後、Unicodeのコードから文字に変換する式だ。CSVファイルと各ページの画像と見比べてみると、実際に読む順番でCSVの行が並んでいるようだ。
式が入っているセルを文字列に変換して、文字コードをUTFにしてCSV保存する。今回は追加した「文字」の列しか使わないが、後日、文字認識と組み合わせたり、ページの画像から文字を自動で切り出したりすることを考えたいので、元のデータは残しておく。
学習用データ、テストデータを生成
まずはCSVデータをpandasで読み込んで、文字列を生成する
import pandas as pd
# CSVをpandasで読み込む(DataFrame型になる)
csv_data = pd.read_csv(filepath_or_buffer="./200003076_coordinate.csv", encoding="utf-8", sep=",")
# "文字"の列を読み出してlistに変換
text_list = csv_data["文字"].values
# listを文字列に変換
text = ''.join(text_list)
# textの内容を確認
print(text)
生成した文字列を表示してみると、このようになっている。
好色一代男卷一目録七歳けした所が戀はじめこしもとに心ある事八歳はづかしながら文言葉おもひは山崎の事九歳人には見せぬところぎやうずいよりぬれの事十歳袖の時雨はかゝるが幸はや念者ぐるひの事十一歳たづねてきくほどちぎり (省略)
学習用・テスト用データとして、文字列を1文字ずつずらして、10文字切り出したものを入力データ、次の文字を正解データとする。たとえばこんな感じ。
| 入力(10文字) | 正解 |
|---|---|
| 好色一代男卷一目録七 | 歳 |
| 色一代男卷一目録七歳 | け |
| 一代男卷一目録七歳け | し |
| 代男卷一目録七歳けし | た |
| 男卷一目録七歳けした | 所 |
# 学習、テスト用データ生成1(先頭からstep文字ずつずらしていき、それぞれmaxlen文字のデータを切り取ってsentencesに格納)
# 正解データnext_charsはmaxlen+1文字目の文字(sentencesの次の文字)
maxlen = 10
step = 1
sentences = [] # 入力データ
next_chars = [] # 正解データ
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
# sentencesのの内容を確認
print(len(sentences))
print(sentences)
次に、各文字に番号をふって、辞書を作成する。
# textから重複しない文字のセットを抽出してlistに変換してソート
chars = sorted(list(set(text)))
# 重複しない文字の数を表示
print(len(chars))
# 文字に番号をふり、文字から番号、番号から文字の辞書を作成
char_indices = dict((char,i) for i, char in enumerate(chars))
indices_char = dict((i,char) for i, char in enumerate(chars))
# 文字から番号の辞書の内容を確認
print(char_indices)
文字数は1717文字だった。データダウンロードページの記載と違うのは、解読できなかった文字が全部「?」に集約されているからだろうか?
辞書を表示してみるとこうなっている。0番が「?」、1番が「あ」、2番が「い」…となっている。
{'?': 0, 'あ': 1, 'い': 2, 'う': 3, 'え': 4, 'お': 5, 'か': 6, 'が': 7, 'き': 8, 'ぎ': 9, 'く': 10, 'ぐ': 11, 'け': 12, 'げ': 13, 'こ': 14, (省略)
最後に学習、テスト用データを、モデルに入力できるように辞書を使ってベクトル化する。
入力データは、1個の学習データにつき、縦軸が切り出した10文字、横軸が文書中の全文字の番号(1717文字)の行列で、1行の中で縦軸の文字に該当する部分だけが1になっている。たとえばこんな感じ。
| - | 26(た) | ... | 74(一) | ... | 123(代) | 387(好) | 1023(男) | 1266(色) |
|---|---|---|---|---|---|---|---|---|
| 好 | 0 | ... | 0 | ... | 0 | 1 | 0 | 0 |
| 色 | 0 | ... | 0 | ... | 0 | 0 | 0 | 1 |
| 一 | 0 | ... | 1 | ... | 0 | 0 | 0 | 0 |
| 代 | 0 | ... | 0 | ... | 1 | 0 | 0 | 0 |
| 男 | 0 | ... | 0 | ... | 0 | 0 | 1 | 0 |
| : | ... | ... | ... | ... | ... | ... | ... | ... |
| た | 1 | ... | 0 | ... | 0 | 0 | 0 | 0 |
このようなデータがsentencesのデータ数(63949)だけ並んだ3次元行列が入力データXになる。
正解データyのほうは、正解は1文字だけなので、
| - | 26(た) | ... | 74(一) | ... | 123(代) | 387(好) | 1023(男) | 1266(色) |
|---|---|---|---|---|---|---|---|---|
| 色 | 0 | ... | 0 | ... | 0 | 0 | 0 | 1 |
のようなデータが、sentencesのデータ数(63949)だけ並んだ2次元行列になる。
# 学習、テスト用データ2(ベクトル化)
import numpy as np
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool) # 入力データ
y = np.zeros((len(sentences), len(chars)), dtype=np.bool) # 正解データ
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
# sentencesのデータ数(len(sentences))が63949だったので、
# 最初から約3/4を学習用データ、残りをテストデータとする
X_Train = X[0:45000]
y_Train = y[0:45000]
X_Test = X[45001:]
y_Test = y[45001:]
モデル生成と学習
LSTMのモデルはUdemyの動画講座TensorFlow・Keras・Python3で学ぶ】時系列データ処理入門のセクション6を参考に作成した。LSTMとは、ニューラルネットの隠れ層の過去の値を次の入力として使うRNNの勾配消失問題を解決したもの(らしい)。
最初は学習パラメータのバッチサイズは128、エポックは30にしてみた。
# モデルを定義する
from keras.models import Sequential
from keras.layers import Dense, Activation, LSTM
from keras.optimizers import RMSprop
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# 学習
result = model.fit(X_Train, y_Train, batch_size=128, epochs=30, verbose=1, validation_data=(X_Test, y_Test))
# テストデータに対して正解率を表示
score = model.evaluate(X_Test, y_Test, verbose=1)
print('Test score:', score[0])
print('Test accuracy:', score[1])
# 【モデルを保存】
model.save("model_komonjo_lstm.h5")
# 【モデルの重みを保存】
model.save_weights("model_komonjo_lstm_weight.h5")
正解率を表示させてみると次のようになった。正解率約10%…かなり微妙な数字だが、ここで高確率で予測できてしまうと、作者は前半だけ自分で書いて、後半はAIに自動で書かせるなんていうこともできてしまうことになるので、こんなものなんだろうか?
Test score: 7.096761063883167
Test accuracy: 0.09900781085074942
実際に、何を入力したら何が予測されているのかを見てみる。
# テストデータ中の文字列を入力して次に来る文字を予測
input_index=1000 # 何番目のテストデータを使うか
x = np.array([X_Test[input_index]]) # 予測モデルに入力するためにarray化
input_str = ""
for i, vec in enumerate(X_Test[input_index]): # 表示用にテストデータの入力を文字列に戻す、1文字ずつ処理
char_index = np.where(vec == True)[0][0] # データがTrueになっている箇所のインデックス
input_str = input_str + indices_char[char_index]
next_char = indices_char[np.where(y_Test[input_index] == True)[0][0]] # テストデータの正解を文字に戻す
print("入力:", input_str)
print("正解:", next_char)
print()
## 次に来る文字を予測
preds = model.predict(x)
prob_index_list = np.argsort(-preds[0]) # predの確率値が高い順にindexを並べ替え
for i in range(10):
print(i+1, "位:", indices_char[prob_index_list[i]] , " 確率:" , preds[0][prob_index_list[i]])
出力結果。うーん、正解が10位以内にも入ってない。
入力: て断りなしに腹の上に
正解: の
1 位: た 確率: 0.4584522
2 位: あ 確率: 0.050318647
3 位: 取 確率: 0.05009877
4 位: 下 確率: 0.043866277
5 位: こ 確率: 0.041676495
6 位: 義 確率: 0.037123315
7 位: え 確率: 0.035473887
8 位: 書 確率: 0.021575177
9 位: も 確率: 0.020057872
10 位: 捨 確率: 0.016927317
予測した文字が正解かどうかだけでなく、予測確率が高い順に10、30、100位以内と、確率0.1%以上に正解が入っている確率を調べてみた。もっとうまく調べる方法がありそうなのだが、思いつかないので地道にチェック。
# 10、30、100位以内 or 確率0.1%以上に正解が入っている確率
top10_count = 0
top30_count = 0
top100_count = 0
percent_count = 0
for i, y in enumerate(y_Test):
x = np.array([X_Test[i]])
preds = model.predict(x)
prob_index_list = np.argsort(-preds[0]) # predの確率値が高い順にindexを並べ替え
correct = np.where(y == True)[0][0] # 正解の文字番号
if correct in prob_index_list[0:10]: # 正解が予測リストの10位以内にあれば→これだと11位以内になる
top10_count = top10_count + 1
if correct in prob_index_list[0:30]: # 正解が予測リストの30位以内にあれば→31位
top30_count = top30_count + 1
if correct in prob_index_list[0:100]: # 正解が予測リストの100位以内にあれば→101位
top100_count = top100_count + 1
if preds[0][correct] >= 0.1: # 正解文字に対するスコアが0.1以上なら
percent_count = percent_count + 1
print("10位以内:" , top10_count/len(y_Test))
print("30位以内:" , top30_count/len(y_Test))
print("100位以内:" , top100_count/len(y_Test))
print("0.1%以上:" , percent_count/len(y_Test))
これもかなり微妙な数字に…
10位以内: 0.3009816339455352
30位以内: 0.42595524593624656
100位以内: 0.5821194849060587
0.1%以上: 0.1381148406164239
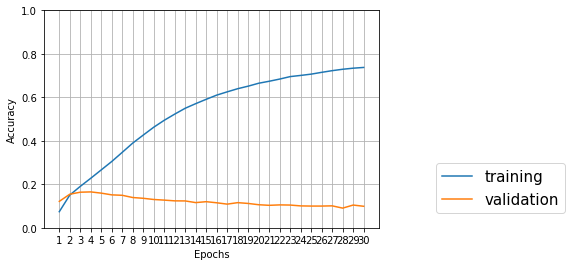
学習結果をプロットするコードを書いて表示させてみよう。
# result.historyに保存された学習データとテストデータに対する正解率をプロット
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(range(1, 30+1), result.history['acc'], label="training") # 学習データ
plt.plot(range(1, 30+1), result.history['val_acc'], label="validation") # テストデータ
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim([0,1])# y軸の最小値、最大値
plt.grid(True) # グリッドを表示
plt.xticks(np.arange(1, 31, 1))
plt.legend(bbox_to_anchor=(1.6, 0), loc='lower right', borderaxespad=1, fontsize=15)
plt.show()
学習用データについては正解率がどんどん上がっているが、テストデータについてはエポック3~4あたりが最高で、だんだん下がっていっている。これは過学習なんだろうか?
入力文字列の長さを変えてみる
入力文字列の長さと、エポック数を変えて何度か試してみた。乱数の種を初期化していないので、同じパラメータで複数回試すと少しずつ数字は異なるが、全体としての傾向はあまり変わらなかった。
Test accuracy: 0.09900781085074942
10位以内: 0.3009816339455352
30位以内: 0.42595524593624656
100位以内: 0.5821194849060587
0.1%以上: 0.1381148406164239
Test accuracy: 0.09734606658576479
10位以内: 0.29114124413021686
30位以内: 0.4103835804358149
100位以内: 0.5692502506199546
0.1%以上: 0.13739249722998997
Test accuracy: 0.12551483789403595
10位以内: 0.362709895448305
30位以内: 0.49978878445453584
100位以内: 0.6562466997571021
0.1%以上: 0.1716654345759848
入力文字列が長い方がちょっと精度が高そうだが、5文字でも20文字でも、エポック3~4あたりがテストスコアの最大値だったので、エポック3で試してみる。
Test accuracy: 0.16701869257774069
10位以内: 0.46219241736191785
30位以内: 0.6263597000739255
100位以内: 0.7769035801034956
0.1%以上: 0.18650332664484107
ちょっと良くなった感じなので、文字数を増やしてみる。
Test accuracy: 0.16678994082840237
10位以内: 0.4642857142857143
30位以内: 0.6266906170752324
100位以内: 0.775993237531699
0.1%以上: 0.19288884192730346
Test accuracy: 0.1646051379654193
10位以内: 0.46368537900412304
30位以内: 0.6264932868167883
100位以内: 0.7773549000951475
0.1%以上: 0.179511576276562
長くしてもあまり変わらない感じなので短くしてみる。
Test accuracy: 0.1668777707409753
10位以内: 0.46289845894025755
30位以内: 0.6293540215326155
100位以内: 0.7735908803039898
0.1%以上: 0.1886214903947646
Test accuracy: 0.16904975465664807
10位以内: 0.46103519231783885
30位以内: 0.6210098665118978
100位以内: 0.7694296417453701
0.1%以上: 0.17538120614150793
Test accuracy: 0.16491690846899512
10位以内: 0.4609337905565814
30位以内: 0.6243207596940121
100位以内: 0.7744658401477182
0.1%以上: 0.1811131627538908
Test accuracy: 0.1387350319182627
10位以内: 0.46035765152714037
30位以内: 0.639605422798966
100位以内: 0.7829297884686396
0.1%以上: 0.15767262752545233
あれ、短くしてもあんまり変わらない?だったら短い方が学習時間が短くて良いのでは?1文字だと正解率はちょっと落ちるけど10位以内とかだとほとんど変わらない。1文字入れて次の文字を予測って、それはもはや時系列処理ではないのでは??
別の作品のデータをテストデータとしてみる
ここまで、学習データと同じ作品の後半部分をテストデータとしてきたが、別の作品のデータでも試してみる。
日本古典籍くずし字データセットには西鶴の他の作品は入っていなかった(2018年12月28日現在)。今回のLSTMでは画像データは不要で、テキストだけあれば良いので、バージニア大学の日本語テキストイニシアチブから好色一代女と、好色五人女の最初の1章をコピペしてテキストファイル化して、テストデータを生成した。
文字列の長さ=1文字、エポック数=3で学習したモデルを使ってテストした。
データの作り方は基本的には同じだが、学習データで作成した辞書にない文字が出てきたときは「?」=番号0を割り当てるようにコードを少しだけ修正した。
f = open("./KoshokuGoninOnna.txt", "r", encoding="utf-8")
text = f.read() # ファイル終端まで全て読んだデータを返す
f.close()
X_Test = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y_Test = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
if char in char_indices:
X_Test[i, t, char_indices[char]] = 1
else:
X_Test[i, t, 0] = 1
if next_chars[i] in char_indices:
y_Test[i, char_indices[next_chars[i]]] = 1
else:
y_Test[i, 0] = 1
結果はこうなった。
同じ作品内のテストデータと比べると、ちょっと正解率が落ちている気もするが、それほど大きな差ではない。
Test accuracy: 0.10565635006131333
10位以内: 0.4295624332977588
30位以内: 0.6056563500533618
100位以内: 0.7737459978655283
0.1%以上: 0.13874066168623267
Test accuracy: 0.11669367910445799
10位以内: 0.4497568881685575
30位以内: 0.6223662884927067
100位以内: 0.7917341977309562
0.1%以上: 0.15883306320907617
次に、日本古典籍くずし字データセットから、別の作者の「雨月物語」をダウンロードして、中の200014740_coordinate.csvから「好色一代男」と同じように文字列を作成して、テストデータとした。
Test accuracy: 0.10679871520342613
10位以内: 0.4148822269807281
30位以内: 0.6092077087794433
100位以内: 0.7769227337615988
0.1%以上: 0.12598144182726623
青空文庫に元禄時代小説第一巻「本朝二十不孝」ぬきほ(言文一致訳)という作品があったので、これも試してみる。テキスト作成時に句読点、記号は削除した。
Test accuracy: 0.06425339366515836
10位以内: 0.34434389140271493
30位以内: 0.5787330316742082
100位以内: 0.8004524886877828
0.1%以上: 0.08235294117647059
正解率、10位以内、30位以内は落ちているが、100位以内は良くなっている謎。言文一致訳なので、仮名遣いが学習データと違っているため、正解率が落ちているのだろうか?
Yahooニュースから「韓国軍がレーダー照射」のニュースのテキストを拾ってきて、句読点、記号、改行を除去したもので試してみた。
Test accuracy: 0.030726257149733645
10位以内: 0.2541899441340782
30位以内: 0.329608938547486
100位以内: 0.5642458100558659
0.1%以上: 0.055865921787709494
仮名遣いも文書の内容も全然違うと、やはり精度はかなり落ちるが、全然違う文書なのに100位以内で50%を超えているのが気になる。
考えてみると、日本語のひらがなは約50文字しかない。文書中のひらがなの比率が高ければ、とりあえずひらがな50文字のどれか、と予測しておけばだいたい当たってしあうのではないだろうか。
学習データの文字出現率をカウント
ということで、元のテキストの文字ごとの出現回数をカウントしてみた。
# 元のテキスト(好色一代男)の各文字の出現回数をチェック
import collections
c = collections.Counter(text_list) # 文字と出現回数の組を取得
print("総文字数:", len(text_list))
print(c)
総文字数: 63959
Counter({'の': 2868, 'し': 2528, 'に': 2416, 'て': 2066, 'は': 1731, 'と': 1611, 'か': 1491, 'も': 1386, 'を': 1377, 'る': 1229, 'な': 1228, ...(省略)
予想通り、ひらがなの出現頻度が高そうだ。これだけだとよくわからないので、10位までの文字と、その比率、1位のみ、1位~10位、1位~30位、1位~100位の文字の、全文字数に対する比率を表示してみた。
num = 0
# print(c.most_common())
for char_count in c.most_common(10): # 出現回数が多い順10個取り出してループ
print(num+1, "位", char_count[0], " ", char_count[1], "回 ", char_count[1]/len(text_list))
num = num + 1
sumcount = 0
num = 0
for char_count in c.most_common(100): # 出現回数が多い順100個取り出してループ
sumcount = sumcount + char_count[1]
if num == 0:
print("1位:", sumcount/len(text_list))
elif num == 10-1:
print("10位まで:", sumcount/len(text_list))
elif num == 30-1:
print("30位まで:", sumcount/len(text_list))
elif num == 100-1:
print("100位まで:", sumcount/len(text_list))
break
num = num + 1
総文字数: 63959
1 位 の 2868 回 0.04484122641066934
2 位 し 2528 回 0.03952532090870714
3 位 に 2416 回 0.03777419909629606
4 位 て 2066 回 0.03230194343251145
5 位 は 1731 回 0.027064213011460468
6 位 と 1611 回 0.025188011069591457
7 位 か 1491 回 0.023311809127722447
8 位 も 1386 回 0.021670132428587063
9 位 を 1377 回 0.021529417282946887
10 位 る 1229 回 0.01921543488797511
1位のみ: 0.04484122641066934
10位まで: 0.2924217076564674
30位まで: 0.5255554339498741
100位まで: 0.7474163135758846
ということで、モデルを作らず、どんな入力に対しても、同じように出現頻度のみに基づく予測結果(1位=の、2位=し、3位=に、...)を出せば、
Test accuracy: 0.04484122641066934
10位以内: 0.2924217076564674
30位以内: 0.5255554339498741
100位以内: 0.7474163135758846
という結果になるだろう。ニュースのテキストと、エポック30の一部これより悪い結果となっているが、それ以外は一応、モデルのほうが予測精度は良くなっている。しかし、あまり大差ないような気がするのは気のせいだろうか。