はじめに

研究データを公平に評価するためには，統計的手法の知識・技術が必要となります．本連載では，Python3を用いた多変量解析の手法をまとめていきます．

ねらい

僕の他にも，実験や研究，仕事などでストックした何かしらのデータを統計的に処理する必要のある方は比較的多いと察します．本連載のねらいは，解析手法の意味や，具体的な利用方法をなるべく簡潔に説明し，これから学習，応用する人の助けになることです．

準備するもの・注意事項

本連載では，python3を中心に，数値計算の簡略化のためにNumPy，SciPyを，グラフを用いた可視化のためにMatplotlibを用います．これらツールを主眼とした説明は本連載では扱いませんが，特にトリッキーな使い方をする気はありません．詳しく知見を深めたい方は以下を参照ください．

1. 情報量

本稿では，2章以降の各解析手法で必要とするデータの情報量の概念，及び統計処理に必要な基礎知識について説明します．

1.1. 平均値

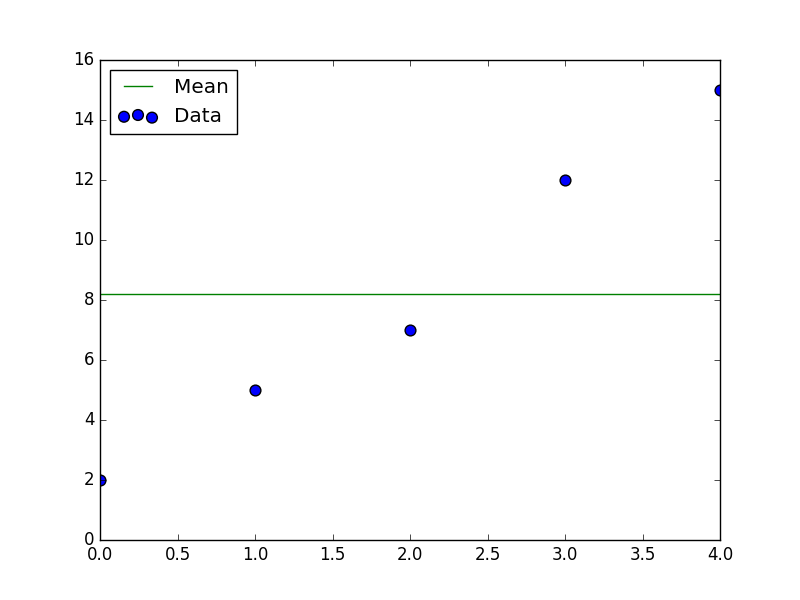
データ集合を統計的に扱う際に，まず集合の平均値を求めます．平均値を求めることで全てのデータの中心的位置を把握することができます．

\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i

ave.py

import numpy as np

data = np.array([2, 5, 7, 12, 15])

print("data: {}".format(data))
print("ave : {}".format(data.mean()))

ave.py

%python3 ave.py
data: [ 2  5  7 12 15]
ave : 8.2

1.2. 偏差

偏差は，各データが平均値（データの中心的位置）からどのくらいの位置に散乱しているかを示します．また，偏差の総和は0になります．これは平均値から上，下にある点までのそれぞれの距離の総和が等しいことを表しています．

x_{d_i} = x_i - \bar{x} \\
\sum_{i=1}^{n}(x_i - \bar{x}) = \sum_{i=1}^{n}x_{d_i} = 0

dev.py

import numpy as np

data = np.array([2, 5, 7, 12, 15])
dev = data - np.ones_like(data) * data.mean()

print("data: {}".format(data))
print("ave : {}".format(data.mean()))
print("dev : {}".format(dev))
print("sum of dev: {}".format(sum(dev)))

dev.py

%python3 dev.py
data: [ 2  5  7 12 15]
ave : 8.2
dev : [-6.2 -3.2 -1.2  3.8  6.8]
sum of dev: 3.552713678800501e-15

実行結果では，偏差の総和は0になっていませんが，限りなく0に近づいた数値となっているため良しとします．

1.3. 偏差平方和

偏差はデータの散らばりを表す数値ですが，データ全体を考えるとその総和は0になるため，全データの散らばりを数量的に表せません．ここで新たに偏差平方和（各偏差の2乗の総和）を定義することで，全データの偏差を数量的に扱えるようにします．

S_x = \sum_{i=1}^{n}(x_i - \bar{x})^2 \\
S_{all} = \sum_{i=1}^{m}\sum_{j=1}^{n}(x_{ij} - \bar{x_i})^2

ssd1.py

import numpy as np

data = np.array([2, 5, 7, 12, 15])
dev = data - np.ones_like(data) * data.mean()
ssd = sum(i ** 2 for i in dev)

print("data: {}".format(data))
print("ave : {}".format(data.mean()))
print("dev : {}".format(dev))
print("sum of dev: {}".format(sum(dev)))
print("sum of sqd dev: {}".format(ssd))

ssd1.py

%python3 ssd1.py
data: [ 2  5  7 12 15]
ave : 8.2
dev : [-6.2 -3.2 -1.2  3.8  6.8]
sum of dev: 3.552713678800501e-15
sum of sqd dev: 110.8

ssd2.py

import numpy as np

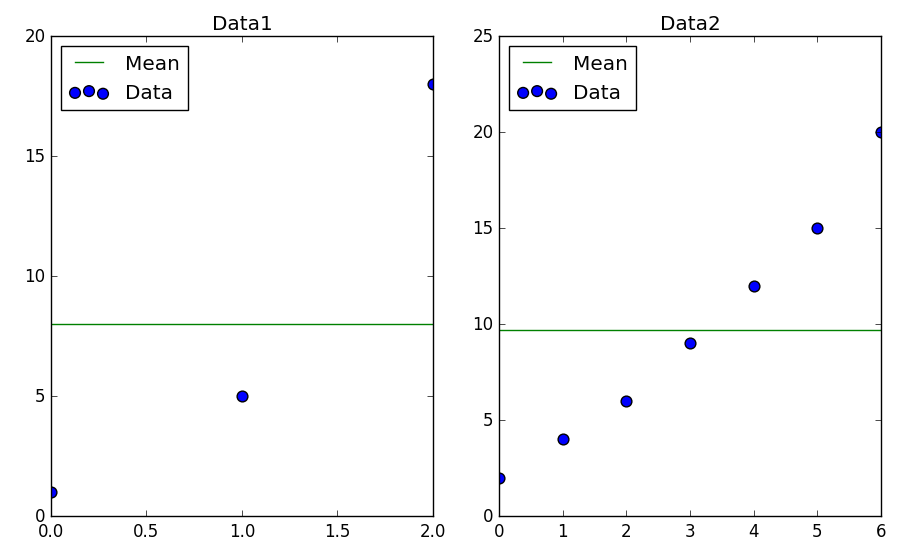
data1 = np.array([2, 5, 7, 12, 15])
data2 = np.array([8, 3, 13, 16, 1])

dev1 = data1 - np.ones_like(data1) * data1.mean()
dev2 = data2 - np.ones_like(data2) * data2.mean()

ssd1 = sum(i ** 2 for i in dev1)
ssd2 = sum(i ** 2 for i in dev2)

print("Amount of info. in data1: {}".format(ssd1))
print("Amount of info. in data2: {}".format(ssd2))
print("Amount of info. in data : {}".format(ssd1 + ssd2))

ssd2.py

%python3 ssd2.py
Amount of info. in data1: 110.8
Amount of info. in data2: 162.8
Amount of info. in data : 273.6

新たに登場した偏差平方和は情報量という捉え方をします．次節以降では，データが持つ情報量を用いて一般的なデータ集合の散らばりを検討します．

1.4. 分散

偏差平方和を用いることで各データの情報量を数量的に捉えることが可能になりました．しかし，偏差平方和では次のようなデータ数が異なる2つのデータ集合のデータの散らばりの度合いを相互に比較することができません．

sva1.py

import numpy as np

data1 = np.array([1, 5, 18])
data2 = np.array([2, 4, 6, 9, 12, 15, 20])

data1_ssd = sum(i ** 2 for i in (data1 - np.ones_like(data1) * data1.mean()))
data2_ssd = sum(i ** 2 for i in (data2 - np.ones_like(data2) * data2.mean()))

print("sum of sqd dev 1: {}".format(data1_ssd))
print("sum of sqd dev 2: {}".format(data2_ssd))

sva1.py

%python3 sva1.py
sum of sqd dev 1: 158.0
sum of sqd dev 2: 245.42857142857144

このようにデータ集合の偏差平方和は，データ数が増加するにしたがって大きくなる傾向にあります．こういった問題に対しては，データ数の尺度を合わせることで対処できます．統計学における分散（標本分散）は，データ集合の偏差平方和をデータ数で除した数値と定義します．

v^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2 \\
s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2

sva2.py

import numpy as np

data1 = np.array([1, 5, 18])
data2 = np.array([2, 4, 6, 9, 12, 15, 20])

data1_ssd = sum(i ** 2 for i in (data1 - np.ones_like(data1) * data1.mean()))
data2_ssd = sum(i ** 2 for i in (data2 - np.ones_like(data2) * data2.mean()))

data1_s = data1_ssd / (len(data1) - 1)
data2_s = data2_ssd / (len(data2) - 1)

print("sum of sqd dev 1: {}".format(data1_ssd))
print("sum of sqd dev 2: {}".format(data2_ssd))
print("sample variance 1: {}".format(data1_s))
print("sample variance 2: {}".format(data2_s))

sva2.py

%python3 sva2.py
sum of sqd dev 1: 158.0
sum of sqd dev 2: 245.42857142857144
sample variance 1: 79.0
sample variance 2: 40.904761904761905

1.5. 標準偏差

分散の平方根を標準偏差と言います．データの単位と同じになるので，分散よりもデータの散らばりを捉えやすくなります．

v = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2} \\
s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2}

sd.py

import numpy as np

data1 = np.array([1, 5, 18])
data2 = np.array([2, 4, 6, 9, 12, 15, 20])

data1_ssd = sum(i ** 2 for i in (data1 - np.ones_like(data1) * data1.mean()))
data2_ssd = sum(i ** 2 for i in (data2 - np.ones_like(data2) * data2.mean()))

data1_sd = (data1_ssd / (len(data1) - 1)) ** 0.5
data2_sd = (data2_ssd / (len(data2) - 1)) ** 0.5

print("standard deviation 1: {}".format(data1_sd))
print("standard deviation 2: {}".format(data2_sd))