ランベルト・ベールの法則の導出とモデルの理解について

はじめに

ランベルト・ベールの法則は、タンパク質の溶液のモル濃度を吸光度計で測定するための原理として利用される。透明に近い溶液に光線を入射させたときその光線の強度は光路長さに対して指数関数的に低下する。濃度が低い場合は、光線の強度の低下率は、単位長さあたりの溶質分子の数に比例するというモデルで再現することができる。そこで、今回はそのモデルを用いて微分方程式を立式する。そして今回はその微分方程式を3つの方法で考察する。1つめは変数分離型という一般的な手法で解く。2つ目は、漸化式と極限の知識を用いて解く。3つめは、計算機を用いた数値計算の手法で視覚的にとらえる。

モデル

以下の図で考える。

青い長方形が溶液でそれに、$I_0$の強度の光線を放つと、光路線距離$L$に対して以下の式が成立する。

溶液の中には、溶質の分子が無数に存在する。1つの分子が吸収することのできる光のエネルギーは同じであると仮定する。このとき、$x=x$から$x=x+\Delta x$での『光線の強度』はその領域内に存在している分子の数に比例する。したがって、単位長さあたりの分子の数と溶液の濃度は比例する。ただし、$|\Delta x|<<1$とする。
つまり、以下の式が成立する。

I(x+\Delta x)=I(x) -(\epsilon^*C\Delta x) I(x)=(1-\epsilon^*C \Delta x) I(x)

ゆえに、以下の式が成立する。

\frac{I(x+\Delta x)-I(x)}{\Delta x}=\frac{dI(x)}{\Delta x}=(-\epsilon^*C) I(x)

ここで、$\Delta x\to 0$とすると、$\Delta x$は$dx$とみなせるので、以下の微分方程式が成立する。

\frac{dI(x)}{dx}=(-\epsilon^*C)I(x)

微分方程式の解法

さて、上記の微分方程式を、3つの見方で分析する。

具体的には、『一般的な変数分離型の解法』、『漸化式と極限の知識を用いた解法』、『計算機を用いた数値計算による視覚化』をそれぞれ紹介する。

変数分離型

さて、上式の微分方程式つまり、

\frac{dI(x)}{dx}=(-\epsilon^*C)I(x)

を解くための一般的な方法を紹介する。

この式は、$x,I(x)$といった変数、関数での関係性を表している。また、右辺と左辺はそれぞれそのパラメータに関して独立ではなく相互に依存しあっている。

そこで、右辺を$x$で表し左辺を$I$で表すことを考える。

\frac{1}{I(x)}dI(x)=(-\epsilon^*C)dx

この式の両辺を$x=0$から$x=L$まで積分する。

\int_{I_0}^{I(L)}\frac{1}{I(x)}dI(x)=\int_{x=0}^{x=L}(-\epsilon^*C)dx

\ln{\frac{I(L)}{I_0}}=-\epsilon^*C L

\frac{I(L)}{I_0}=e^{-\epsilon^*C L}

I(L)=I_0 e^{-\epsilon^{ *}CL}

このような微分方程式の解法を変数分離型による解法と呼ぶ。

漸化式による解法

この方法は、上記解法のようにシステマティックな方法ではなく、漸化式と極限を用いた解法で高校数学の範囲で説明できる。したがって、東工大などの最難関大の物理ではたまに出題される。漸化式は、$n$番目ととなりの$n+1$番目の数値の関係性を示すといったものである。このままだと、離散的（とびとびの値を取ってしまうという性質）である。しかし、たとえ離散的でもその間隔を小さくしていけばいつかは連続的（滑らかにつながっているという性質）を再現できるだろうとい仮定を今回は用いる。　

ここで、以下の式を考察する。

I(x+\Delta x)=(1-\epsilon^*C \Delta x) I(x)

$\Delta x=L/n$とし、$x_0=0,x_k=k\Delta x$,$(0\le k \le n)$とすると、

I(x_{n+1})=(1-\epsilon^*C \Delta x) I(x_{n})

と表せる。ただし、$I(x_0)=I_0$とする。

そこで、等比数列の漸化式より、

I(L)=I(x_{n})=(1- \frac{\epsilon^*C L}{n})^n I_0

ここで、$n\to \infty$のとき、

(1+\frac{1}{n})^n\to e

なので、

I(L)=I(x_{n})=(1-\epsilon^*C \frac{L}{n})^n I_0=\{(1- \frac{\epsilon^*C L}{n})^{-\frac{n}{\epsilon^*C L}}\}^{-\epsilon^*C L} I_0

と変形できるので、$n\to \infty$のとき、

I(L)\to I_0e^{-\epsilon^*C L}

数値計算

以下の式を漸化式を計算機を用いて数値計算することを考える。

I(x+\Delta x)=I(x) -(\epsilon^*C\Delta x) I(x)=(1-\epsilon^*C \Delta x) I(x)

そこで、簡易的なプログラムを作成した。

python lambert_vale.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

L_max=10 # 光の透過距離の最大値
n=1000
L_ary=np.linspace(0, L_max, n)

#ε*は物質のモル吸光係数であるがプログラムではepsilonとする
# Cは物質の濃度である
epsilon=1

C=1.0
I_ary=np.zeros(n)
delta_L=L_max/n
# ランベルト・ベールの法則に基づく光の強度の減衰を数値的に計算
# I(L) = I(0) * exp(-εCL)

# I(0) = 1.0 として計算
I_ary[0]=1.0

for i in range(1,n):
    I_ary[i]=I_ary[i-1]-epsilon*C*I_ary[i-1]*delta_L
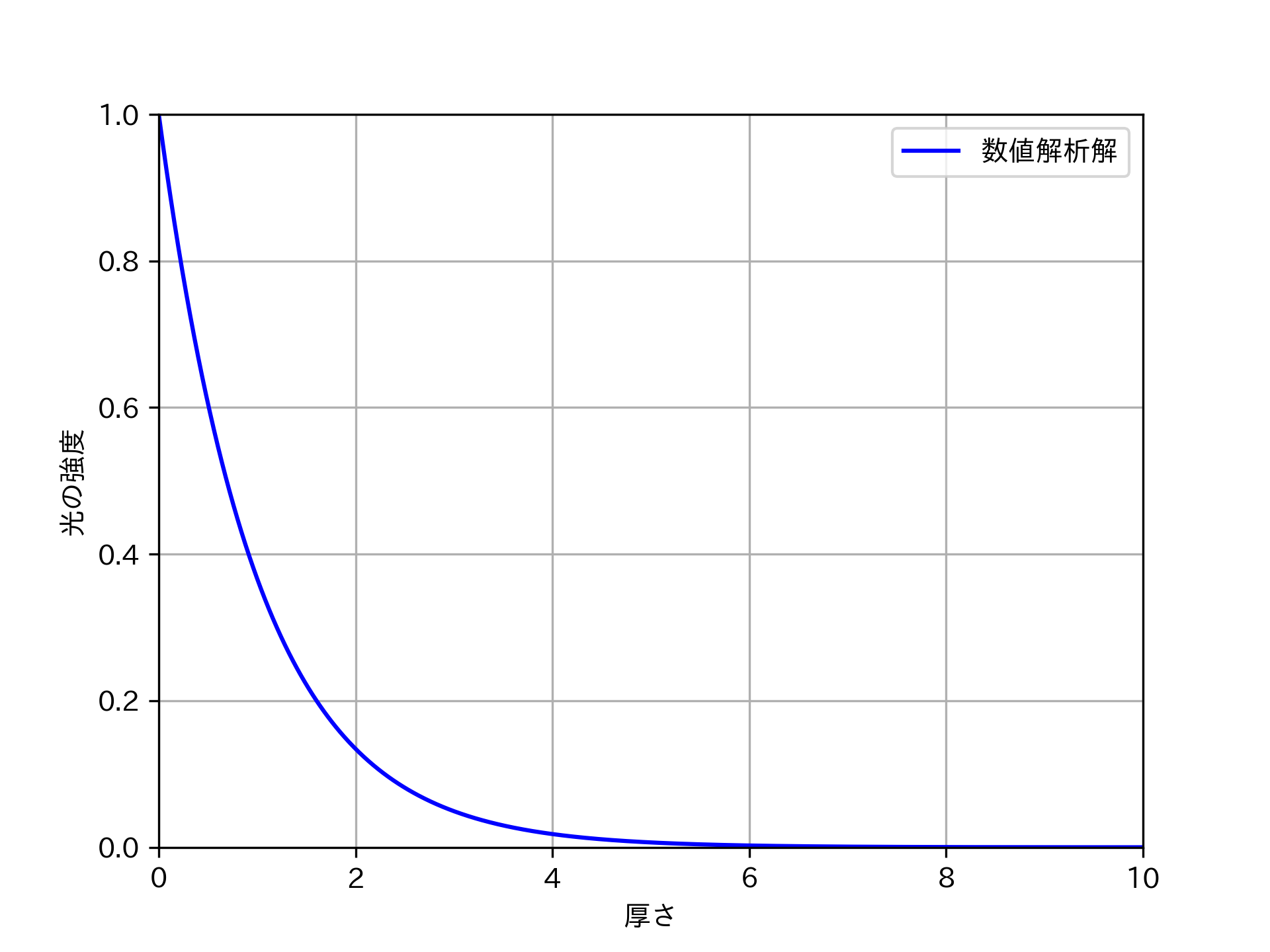
plt.plot(L_ary, I_ary, color="blue",label="数値解析解")
#plt.plot(L_ary, np.exp(-epsilon*C*L_ary), color="red", label="解析解")
plt.xlabel("厚さ")
plt.ylabel("光の強度")
plt.grid()
plt.ylim(0,1)
plt.xlim(0, L_max)
plt.legend()
plt.savefig("ランベルト_ベールの法則_数値解析.png", dpi=300)
plt.show()

これを実行すると以下のようなグラフが出力される。

一方で、このプログラムだと濃度が異なることによって、どのように光線の減衰に差がでるのかを評価できないため、以下のようにプログラムを書き換える。

python lambert_vale_con.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import matplotlib.cm as cm

L_max = 10
n = 100  # 厚さ方向の分割数
m = 10   # 濃度の分割数
L_ary = np.linspace(0, L_max, n)
epsilon = 1
C_ary = np.linspace(0.1, 1.0, m)

delta_L = L_max / n

# カラーマップの設定（jetでm段階に分ける）
colors = cm.jet(np.linspace(0, 1, m))

plt.figure(figsize=(10, 6))

for k in range(m):
    C = C_ary[k]
    I_ary = np.zeros(n)
    I_ary[0] = 1.0
    for i in range(1, n):
        I_ary[i] = I_ary[i-1] - epsilon * C * I_ary[i-1] * delta_L
    plt.plot(L_ary, I_ary, color=colors[k], label="C={:.1f}".format(C))

plt.xlabel("厚さ")
plt.ylabel("光の強度")
plt.grid()
plt.ylim(0, 1)
plt.xlim(0, L_max)
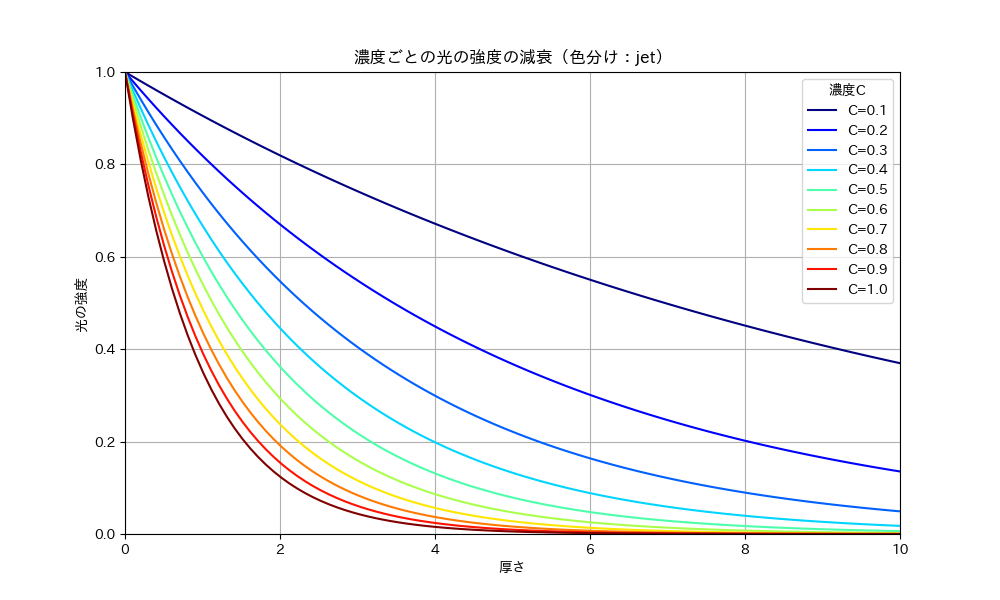
plt.title("濃度ごとの光の強度の減衰（色分け：jet）")
plt.legend(title="濃度C")
plt.savefig("光の強度と厚さと溶液の濃度の関係.png")
plt.show()

これを実行すると以下のようなグラフが出力される。

このように、濃度が高い程、光線をより多くの分子が吸収してしまうので、光線が減衰しやすい。そのことを利用して吸光度計でタンパク質のモル濃度を測定することができる。

まとめ

今回は、分析化学のタンパク質のモル濃度測定法の原理として、ランベルト・ベールの法則を紹介した。ランベルト・ベールの法則を実生活でイメージするための例としては、少し汚れたガラスを重ねていくとその末端から見える光の強度は低下していくという例がある。また、式的には放射性物質の半減期にも似ている。なので、このような分野を別々に学ぶのではなく、関連付けながら学習することが何よりも大切であると考えられる。
また、それらを理解するために、抽象度の高い大学数学を道具として用いるのではなく、分かりやすい高校数学に次元を下げて考えたり、プログラムを用いてグラフを図示したりすることがも大切であると考えられる。

参考文献