送電線伝送線路における数値計算

はじめに

電気回路には2つの考え方がある。1つは、抵抗、リアクトル、コンデンサ素子が一点に集中して配置されているという考え方である。（集中定数回路）
もう一点は、広い範囲に分布しているという考え方である。(分布定数回路)

長距離送電線では、分布定数回路という考え方を用いる。これは、等間隔に同じRLC回路が繰り返し構成されているという考え方に基づいている。

そこで、今回はPYthonを用いて、分布定数回路の数値計算を行う。
具体的には抵抗成分を無視したL,C分で構成される長距離送電線もしくはケーブルを考える。

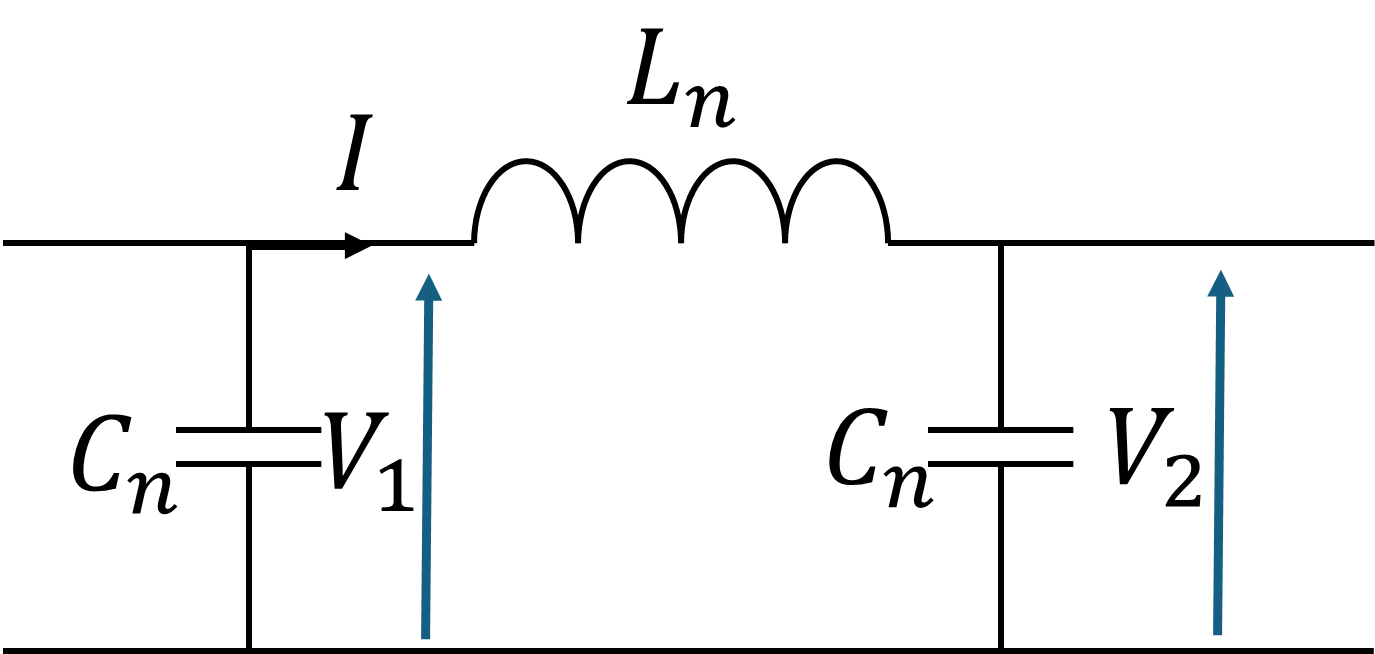
問題設定

以下に、1単位の等価回路を示す。

回路方程式

この場合、以下の式が成立する。

V_1(t)-V_2(t)=L_n \frac{dI(t)}{dt}

V_2(t+\Delta t) =V_2(t)+\frac{I(t)\Delta t}{C_n}

プログラム

この条件の下で、以下のようなプログラムを作成した。

ただし、近似精度を上げるべく、台形の面積公式である以下の式を用いた。

\int _{t}^{t+\Delta t} I(t)dt \sim \frac{1}{2}(I(t)+I(t+\Delta t))\Delta t

python transmission_line.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

n=100
m=n
#線路全体のパラメータ
L=0.01
C=1
#振幅
A=1.0
t_max=0.05
x_max=1e4
dt=t_max/(m-1)
dx=x_max/(n-1)
t_ary=np.linspace(0,t_max,m)
x_ary=np.linspace(0,x_max,n)
t_ary,x_ary=np.meshgrid(t_ary,x_ary)
omega=2*math.pi*50

V_ary=np.zeros((m,n))
I_ary=np.zeros((m,n))

#i:時間
for i in range(m-1):
#k:変位
    for k in range(0,n-1):
        if k==0:
            t=i*dt
            V_ary[i][k]=A*math.sin(omega*t)
            
        else:
            V1=(V_ary[i][k]-V_ary[i][k-1])/dx
            V2=(V_ary[i][k+1]-V_ary[i][k])/dx
            VV=V2-V1
            dL=L/n
            dC=C/n
            dIdt=(1/dL)*(VV)
            I_ary[i+1][k]=I_ary[i][k]+dIdt*dt
            I_ary_ave=0.5*(I_ary[i+1][k]+I_ary[i][k])
            V_ary[i+1][k]=V_ary[i][k]+(1/dC)*I_ary_ave*dt
            #V_ary[i+1][k]= V_ary[i][k]+(1/dR)*VV*dt/(omega*dC) 
                  
levels = np.linspace(0, t_max/10, 20)
plt.contour(x_ary,V_ary,t_ary,levels,cmap='jet')
plt.xlabel("距離x [m]")
plt.ylabel("電圧V [V]")
plt.title("伝送線路における電圧の時間・距離変化")
plt.colorbar(label='時間t [s]')
plt.savefig('伝送線路における電圧の時間・距離変化.png')
plt.show() 

plt.contour(x_ary,I_ary,t_ary,levels,cmap='jet')
plt.xlabel("距離x [m]")
plt.ylabel("電流I [A]")
plt.title("伝送線路における電流の時間・距離変化")
plt.colorbar(label='時間t [s]')
plt.savefig('伝送線路における電流の時間・距離変化.png')
plt.show() 

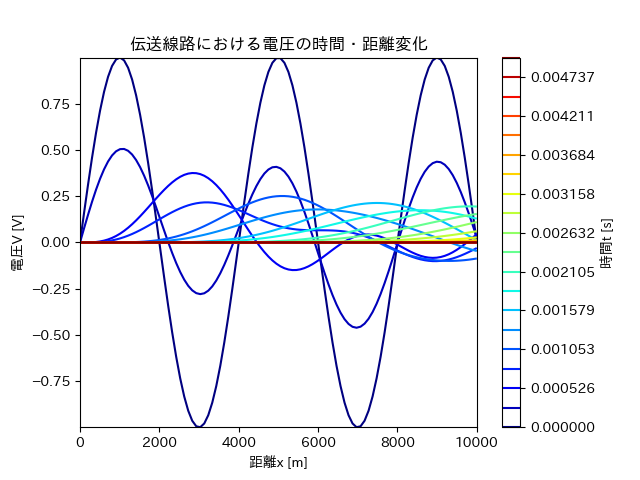
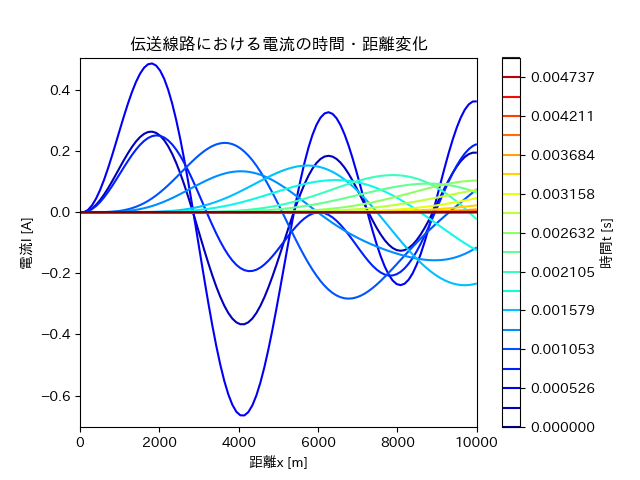
結果

これを実行すると、以下のようなグラフが得られた。

電圧

電流

このように、時間経過とともに減衰し、長距離になるほど位相がずれていくことがわかる。

まとめ

今回は、Pythonを用いた伝送線路の数値計算を行った。伝送線路を厳密に考察する場合は、偏微分方程式を用いる必要性があり、数学的にはかなり難しい。そこで、今回は数値計算を行うことでシミュレートした。

参考文献