はじめに
三角関数の合成公式を理解するのはかなり難しい。合成公式の使い方自体は、同じ位相(角度)の正弦と余弦で表された2変数関数を1変数関数で置き換えることができるというものが有名ではある。しかし、なぜ合成公式が成立するのかはあまり言及されない。そこで、今回は三角関数の合成公式がなぜ成立するのかを調査する。具体的には、三角関数の合成公式とは、正弦の加法定理の右辺と左辺を入れ替えただけのものである。
合成公式とは
合成公式は、以下のように同じ角度を持つ正弦と余弦の和を別の角度の正弦のみで表すというものである。
A\sin{\theta}+B\sin{\theta}=\sqrt{A^2+B^2}\sin{(\theta+\alpha)}
ただし、$\theta$は以下の三角形の角度とする。($\tan{\alpha}=\frac{B}{A}$とすれば、鈍角でも成立する。)
さて、これを証明したいが、右辺の$\sin{(\theta+\alpha)}$は紛れもなく、正弦の加法定理を用いて展開できる。
\sin{(\theta+\alpha)}=\sin{\theta}\cos{\alpha}+\cos{\theta}\sin{\alpha}
なので、
\sin{(\theta+\alpha)}=\cos{\alpha}\sin{\theta}+\sin{\alpha}\cos{\theta}
両辺に、$R=\sqrt{A^2+B^2}$となる$R$を掛けてみる。
R\sin{(\theta+\alpha)}=(R\cos{\alpha})\sin{\theta}+(R\sin{\alpha})\cos{\theta}
ここで、上図より、
A=R\cos{\alpha},B=R\sin{\alpha}
なので、
R\sin{(\theta+\alpha)}=A\sin{\theta}+B\cos{\theta}
が成立する。両辺を入れ替えると題意が成立する。
自分が受験生のときは、合成公式がなんとなく不気味に感じられた。理由は、解き方としては使えるけどなんでこの解き方でいいのか自信がなかったからである。だが、正弦の加法定理の右辺と左辺を入れ替えただけのものに過ぎないと分かってからは腑に落ちた。このように、同じ式でも逆から見る(右辺→左辺)と新たな解法がひらめく場合があるので、柔軟な思考力を身に着けたい。
素朴な疑問
正接は置いておいて、余弦の場合でも合成の公式のようなものは導出できるのだろうか?以下に、余弦の場合の加法定理の右辺と左辺を入れ替えたものを示す。
\cos{\alpha}\cos{\theta}+\sin{\alpha}\sin{\theta}=\cos{(\theta-\alpha)}
ここで、正弦の加法定理と同様、両辺に$R=\sqrt{A^2+B^2}$となる$R$を掛けてみる。
R\cos{\alpha}\cos{\theta}+R\sin{\alpha}\sin{\theta}=R\cos{(\theta-\alpha)}
ここで、
A=R\cos{\alpha},B=R\sin{\alpha}
なので、
A\cos{\theta}+B\sin{\theta}=R\cos{(\theta-\alpha)}
これは、正弦の加法定理と果たして同じようなもの(矛盾しない
)なのだろうか。
合成の公式を用いて以下のような計算をする。
B\sin{\theta}+A\cos{\theta}=R\sin{\{\theta+(\frac{\pi}{2}-\alpha)\}}=R\sin{\{\frac{\pi}{2}+(\theta-\alpha)\}}=R\cos{(\theta-\alpha)}
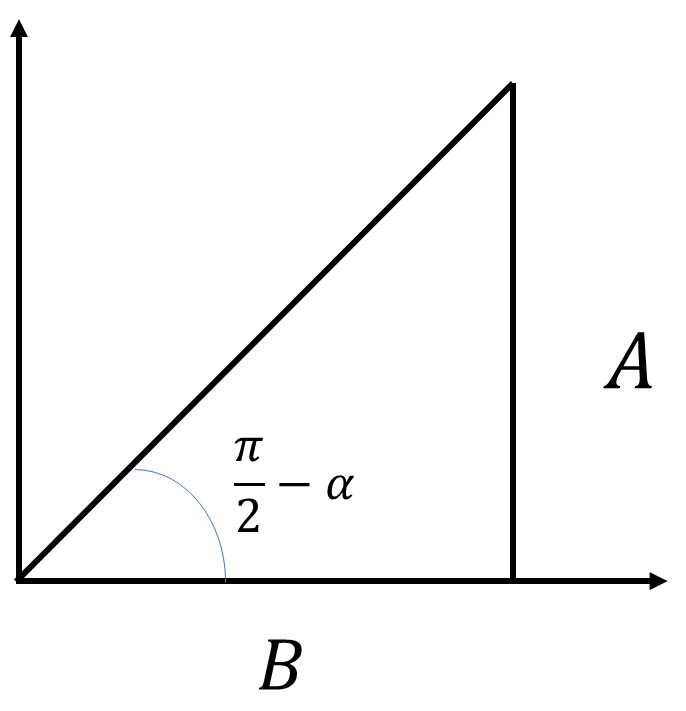
ただし、以下の三角形で考えていることに注意する。
したがって、上記の議論より、余弦の加法定理からも同様な合成公式を導くことができる。したがって。わざわざ正弦の場合と余弦の場合に分けて合成公式を覚えるなどしなくてもよい。
まとめ
三角関数の分野はいろいろな公式があるので難しく感じがちである。しかし、三角関数の加法定理さえしっかりと理解できれば、それ以外の公式はすべて導出可能である。なので、受験生は三角関数を公式の暗記ゲーだと思うのではなく、三角関数の加法定理を軸としてしっかりと体系立てて理解したいものである。