はじめに
電力系統の最も単純なモデルは、発電設備、送電設備、変電設備、需要家から構成される。
ただし、変電設備は単位法を用いることで上手く扱える場合も多い。
そこで、今回は発電機、リアクトル送電線、RL負荷から構成される最も平易な電力系統の解析をPythonを用いて実施する。
系統構成
系統構成は、以下の通りとする。
前提条件
・負荷側の周波数は、(あり得ないが)近似的に常に一定であるとする。
・発電機の電圧の大きさは常に一定であるとする。
理論式
動揺方程式
同期発電機の機械的回転角を$\theta$とする。
発電機の慣性定数を$M$とすると、動揺方程式は以下のように表すことができる。
M\frac{d^2\theta}{dt^2}=P_m-P_e
\theta = \omega_s t +\delta
ただし、$\delta$は機械角と電気角の位相差である。
送電モデル式
受電端有効電力及び、無効電力は以下の式により与えられる。
P_e=\frac{EV}{X_1}\sin \delta,Q_e=\frac{(E\cos\delta-V)V}{X_1}
アルゴリズム
ここで、$P_e:Q_e=R:X_2$であることから、
$err =(P_e X_2-R Q_e)^2$となる目的関数を最小にする電圧$V$を最急降下法で推定する。
また、動揺方程式の数値計算は1次のオイラー法を用いて計算する。
プログラム
以下のようなプログラムを作成した。
import math
import matplotlib.pyplot as plt
import japanize_matplotlib # 日本語フォント設定用(インポートするだけで有効)
# ------------------------------------------------------------
# 単機無限大母線系統の動揺を簡易モデルでシミュレーションするスクリプト
#
# ・同期発電機の内部起電力 E(一定)と端子電圧 V を仮定
# ・簡易潮流条件(P, Q)から V を最急降下法で求める
# ・求めた V を用いて電気出力 P_e を計算し、動揺方程式から δ(t) を更新する
# ------------------------------------------------------------
# ====== 系統・機器パラメータ =====================================
# 慣性定数(単位慣性:pu 系)… 動揺方程式 d^2δ/dt^2 = (P_m - P_e) / M で使用
M = 1.0
# 初期の機械角(電気角)[rad]
theta = 18 * math.pi / 180
# 発電機内部電圧 E と端子電圧 V 間の等価リアクタンス [pu]
X_1 = 1.0
# 系統側の等価インピーダンス R + jX_2 [pu]
# ここでは無限大母線までの等価インピーダンスを単純モデル化
R = 1.0
X_2 = 1.0
# 機械入力(タービン出力)[pu]
P_m = 0.1
# 発電機内部起電力(一定と仮定)[pu]
E = 1.0
# ====== 数値計算パラメータ =====================================
# V に対する微小変化量(偏微分の近似用)
dV = 1e-3
# 最急降下法のステップ幅(学習率に相当)
alpha = 0.01
# 系統周波数 [Hz]
f = 50.0
# 同期角速度 [rad/s]
omega_s = 2.0 * math.pi * f
# 計算時間ステップ [s]
delta_t = 1e-3
# 端子電圧の初期値 [pu]
V = 1.0
# 機械角 θ の一次微分(角速度偏差に相当)[rad/s]
d_theta = 0.0
# シミュレーション時間 [s]
t_max = 10.0
# ====== 結果保存用配列 =========================================
P_e_ary = [] # 電気出力 P_e(t) [pu]
V_ary = [] # 端子電圧 V(t) [pu]
delta_ary = [] # 相差角 δ(t) [rad]
t_ary = [] # 時刻 t [s]
# ====== 関数定義 ================================================
def err_V(V, delta):
"""
与えられた相差角 delta に対して、端子電圧 V を仮定したときの
潮流条件の「誤差」を評価する関数。
P_e = (E * V / X_1) * sin(delta)
Q_e = (E * V / X_1) * cos(delta) - (V**2 / X_1)
としたとき、
(Q_e * R - P_e * X_2)^2
を最小化するように V を決める。
"""
P_e = E * V / X_1 * math.sin(delta)
Q_e = E * V / X_1 * math.cos(delta) - V ** 2 / X_1
err = (Q_e * R - P_e * X_2) ** 2
return err
def opt_V(V0, delta):
"""
相差角 delta が与えられたときに、端子電圧 V を最急降下法で最適化する。
Parameters
----------
V0 : float
V の初期値 [pu]
delta : float
相差角 δ [rad]
Returns
-------
V : float
誤差関数 err_V(V, delta) が十分小さくなるまで更新した V
"""
V = V0
while err_V(V, delta) > 1e-3:
# 数値微分による d(err)/dV の近似
derr_dV = (err_V(V + dV, delta) - err_V(V, delta)) / dV
# 最急降下法による更新
V = V - alpha * derr_dV
return V
# ====== 時間応答シミュレーション ===============================
t = 0.0
while t <= t_max:
# 相差角 δ = 機械角 θ - 系統基準角(ω_s t)
delta = theta - omega_s * delta_t
# 時刻保存
t_ary.append(t)
# 電圧 V を最適化(潮流条件を満たす V を探索)
V = opt_V(V, delta)
# 電気出力 P_e 計算
P_e = E * V / X_1 * math.sin(delta)
# 運動方程式(swing 方程式の簡易オイラー解法)
dd_theta = (P_m - P_e) / M # 角加速度 d^2θ/dt^2
# 結果配列に保存
P_e_ary.append(P_e)
delta_ary.append(delta)
V_ary.append(V)
# オイラー法による積分
d_theta = d_theta + dd_theta * delta_t # 角速度更新
theta = theta + d_theta * delta_t # 角度更新
t = t + delta_t # 時間更新
# ====== グラフ描画 ==============================================
# 相差角 δ(t)
plt.figure()
plt.plot(t_ary, [d * 180 / math.pi for d in delta_ary])
plt.xlabel('時間 [s]')
plt.ylabel('位相角 δ [deg]')
plt.grid(True)
plt.savefig('delta.png')
plt.show()
# 端子電圧 V(t)
plt.figure()
plt.plot(t_ary, V_ary)
plt.xlabel('時間 [s]')
plt.ylabel('電圧 V [pu]')
plt.grid(True)
plt.savefig('voltage.png')
plt.show()
# 電気出力 P_e(t)
plt.figure()
plt.plot(t_ary, P_e_ary)
plt.xlabel('時間 [s]')
plt.ylabel('電力 P_e [pu]')
plt.grid(True)
plt.savefig('power_e.png')
plt.show()
結果
以下、結果を示す。
安定な場合
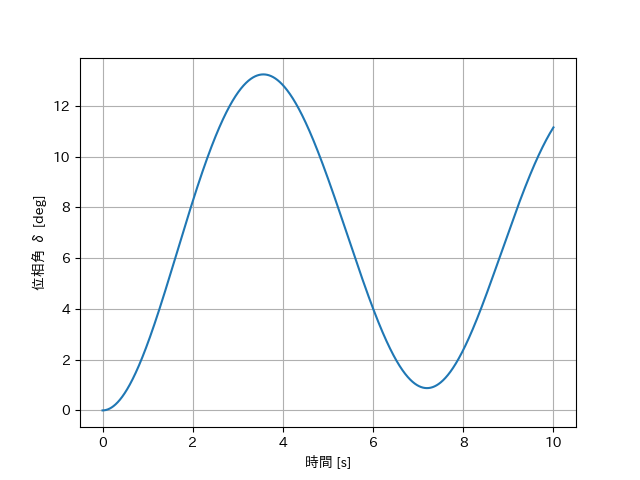
位相角
このように、位相角は約12度を最大値にとった。したがって、90度以下であったため脱調現象による不安定は回避することができた。
母線電圧
一方で、電圧は上下を繰り返しているが、ほぼ一定の範囲内に収まっている。したがって、安定的に電力を送電できていることがわかる。
受電端電力
振動しているが、時間経過とともに、安定しているのがわかる。
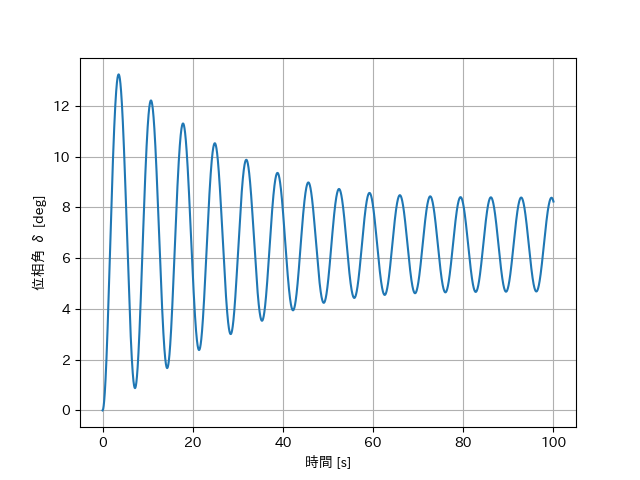
参考までに、$10$倍の時間での解析をした結果も示す。
位相角
母線電圧
受電端電力
不安定な場合(脱調時)
次に、脱調した場合の結果を示す。(機械的入力を10倍とした)
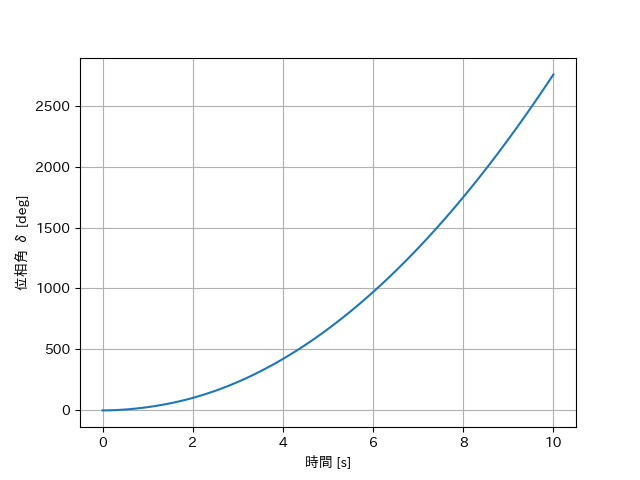
位相角
このように、位相角は指数関数的に増加していく。
母線電圧
母線電圧も急激に低下し、ほぼ0となった。
受電端電力
電力もほぼ0付近で振動をしてしまった。
まとめ
今回は、単純な系統モデルのシミュレーションを行った。実際の系統の特性とはかけ離れている部分もある粗いモデルではあるが、ある程度ポイントとなる特性をみることができた。
参考文献