はじめに
直流電気回路の電圧および電流を測定する場合は、電圧計および電流計が使用される。しかし、電力を測定したい場合は、電圧計と電流計を対象に接続して積を計算することで算出することができる。
しかし、電圧計および電流計の示す値は一般的に誤差が含まれている。したがって、それらの積で電力を計算した場合、電圧計と電流計の誤差の両方を考慮する必要性がある。
そこで、今回は、電圧および電流の誤差が測定値よりも十分に小さい場合において電力の誤差がどのような特性を示すのかを評価する。
直流電力の誤差について
理想的な回路において、電圧$V$および電流$I$の積として電力$P$が表現されるとする。
ここで、実際の測定では誤差を含むので、測定値の電圧および電流、電力がそれぞれ、$V+\Delta V,I+\Delta I,P+\Delta P$であったとすると、以下のことが成立する。
P=VI
(P+\Delta P)=(V+\Delta V)(I+\Delta I)
ここで、2次の微小量は無視できるほど電圧と電流の誤差が小さいと仮定する。
\Delta P=V\Delta I+I \Delta V
ここで、両辺を、
P=VI
で除すると以下のようになる。
\frac{\Delta P}{P}=\frac{\Delta V}{V}+\frac{\Delta I}{I}
つまり、各測定値の誤差を$err_P,err_V,err_I$とすると、以下の式が近似的に成立する。
err_P=err_V+err_I
今回は、この誤差に対する近似式が成立するかどうか計算機によって確かめる。
回路設定
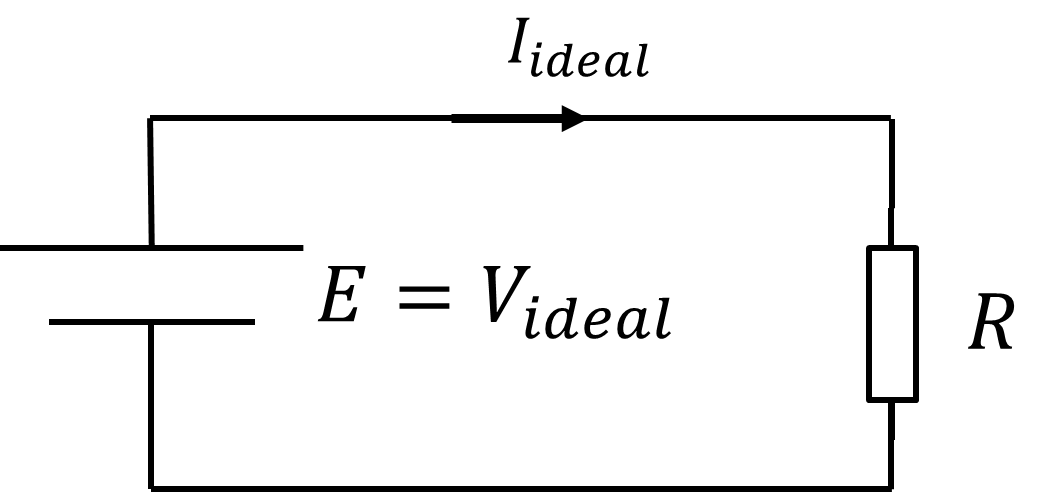
起電力$E$の電池に抵抗$R$接続した以下の理想的な回路を考える。
しかし、実際には電池、電圧計、電流計には内部抵抗があると考えられる。
(今回は抵抗Rの誤差は考えない)
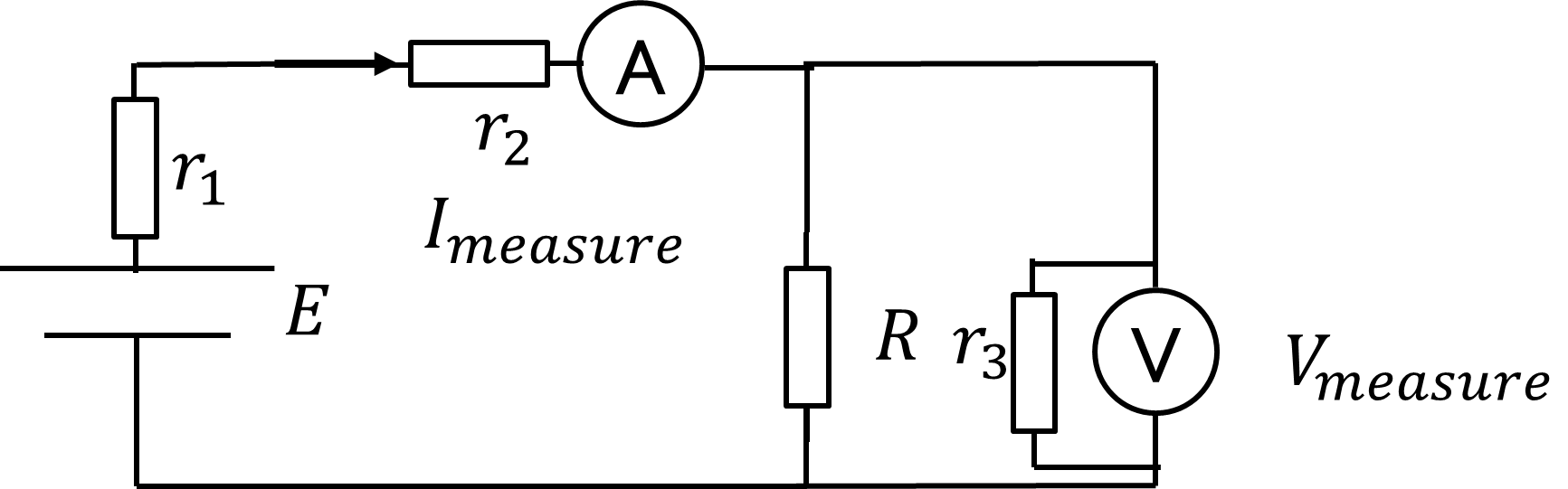
したがって、実際の回路は以下のようになる。
なので、まず真値は以下のようになる。
P_{ideal}=V_{ideal}I_{ideal}
一方で、実際の測定結果は以下のようになる。
P_{measure}=V_{measure}I_{measure}
したがって、各計測値の誤差を以下のように定義する。
err_P=\frac{P_{measure}-P_{ideal}}{P_{ideal}}
err_V=\frac{V_{measure}-V_{ideal}}{V_{ideal}}
err_I=\frac{I_{measure}-I_{ideal}}{I_{ideal}}
この場合、以下の式が近似的に成立するかを検証する。
err_P=err_V+err_I
これが成立すれば、$err_V,err_I,err_P$の関係は3次元で表すと線形上になるはずである。
プログラム
$r_1,r_2,r_3$の値をある範囲内でランダムに$n$個生成し、それに対する応答$P,V,I$の分布を3次元でプロットする。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#電池の起電力
E=1.0 #[V]
#計測負荷
R=1.0#[Ω]
def measure_err(r1,r2,r3):
# #電池の内部抵抗r1[Ω]
# #電流計内部抵抗r2[Ω]
# #電圧計内部抵抗r3[Ω]
V_ideal=E
I_ideal=E/R
P_ideal=V_ideal*I_ideal
RR=(R+r3)/(R*r3)
I_measure=E/(r1+r2+RR)
V_measure=R*(r3/(R+r3))*I_measure
P_measure=V_measure*I_measure
delta_P=P_measure-P_ideal
delta_V=V_measure-V_ideal
delta_I=I_measure-I_ideal
err_P=delta_P/P_ideal
err_V=delta_V/V_ideal
err_I=delta_I/V_ideal
return err_P,err_V,err_I
n=1000
r1_ary=np.random.randn(n)*1e-6
r2_ary=np.random.randn(n)*1e-6
r3_ary=np.random.randn(n)*1e+6
err_P_ary=[]
err_V_ary=[]
err_I_ary=[]
for i in range(n):
r1=r1_ary[i]
r2=r2_ary[i]
r3=r3_ary[i]
err_P,err_V,err_I=measure_err(r1,r2,r3)
err_P_ary.append(err_P)
err_V_ary.append(err_V)
err_I_ary.append(err_I)
fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection': '3d'})
ax.scatter(err_V_ary, err_I_ary, err_P_ary)
ax.set_xlabel("V_err")
ax.set_ylabel("I_err")
ax.set_zlabel("P_err")
plt.savefig("VIP要素の測定誤差の関係性.png")
plt.show()
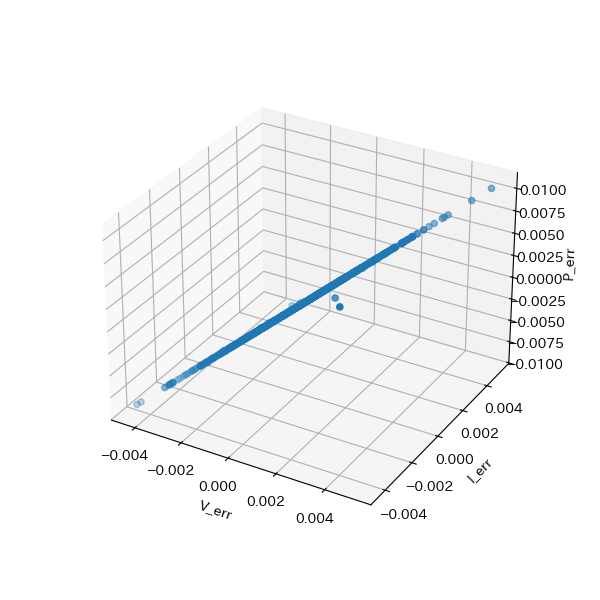
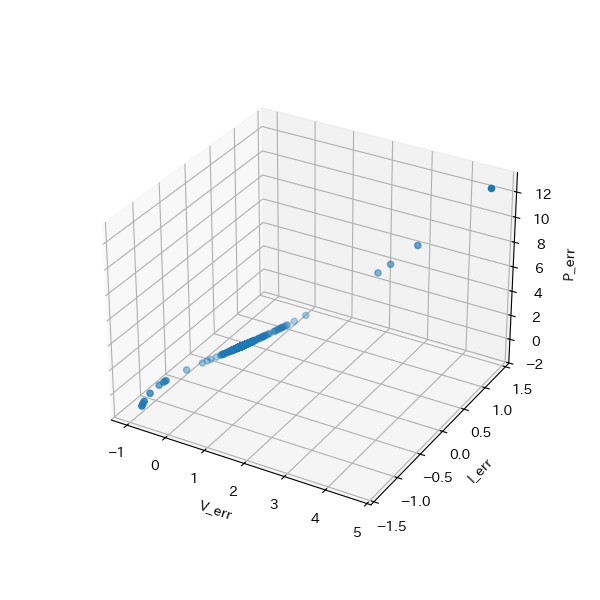
結果、以下のようにほぼ線形になった。
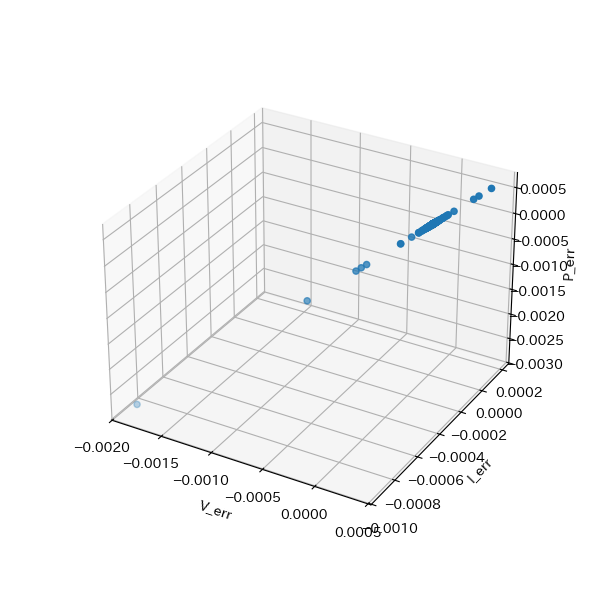
ただし、電圧計の内部抵抗を小さく、電流計、電池の内部抵抗を大きくすると、以下のようにばらつき始めた。
その傾向をさらに強めると、線形性から少しずれたような分布を示すようになってしまった。。
このことから、
\frac{\Delta P}{P}=\frac{\Delta V}{V}+\frac{\Delta I}{I}
の近似式は、あくまで2次の微小量が対象に対して無視できるほど小さい場合にしか用いることができないということが分かった。
まとめ
今回は、電力の測定と誤差の評価という身近な問題を扱った。具体的には、微小量の積が無視できる場合にしか今回の近似式は適用できないということを計算機を用いて視覚的に示した。だが、それらが無視できるような条件であれば、美しい線形関係が現れることも分かった。