ランダムウォークと粒子の拡散現象について

はじめに

水中に、親和性の高い物質（例えば食塩）を溶かすことを考える。食塩は水中を攪拌しなくてもある程度は拡散されていく。一般に、統計力学では、溶媒物質（この場合は食塩）を質点である球体粒子（分子）の集合体であると見なすことから議論を始める。そこで、今回は各食塩の粒子が微小時間$\Delta t$ごとにランダムな方向において一定距離だけ移動するというモデル（ランダムウォーク）を考えることで、拡散現象について調査する。

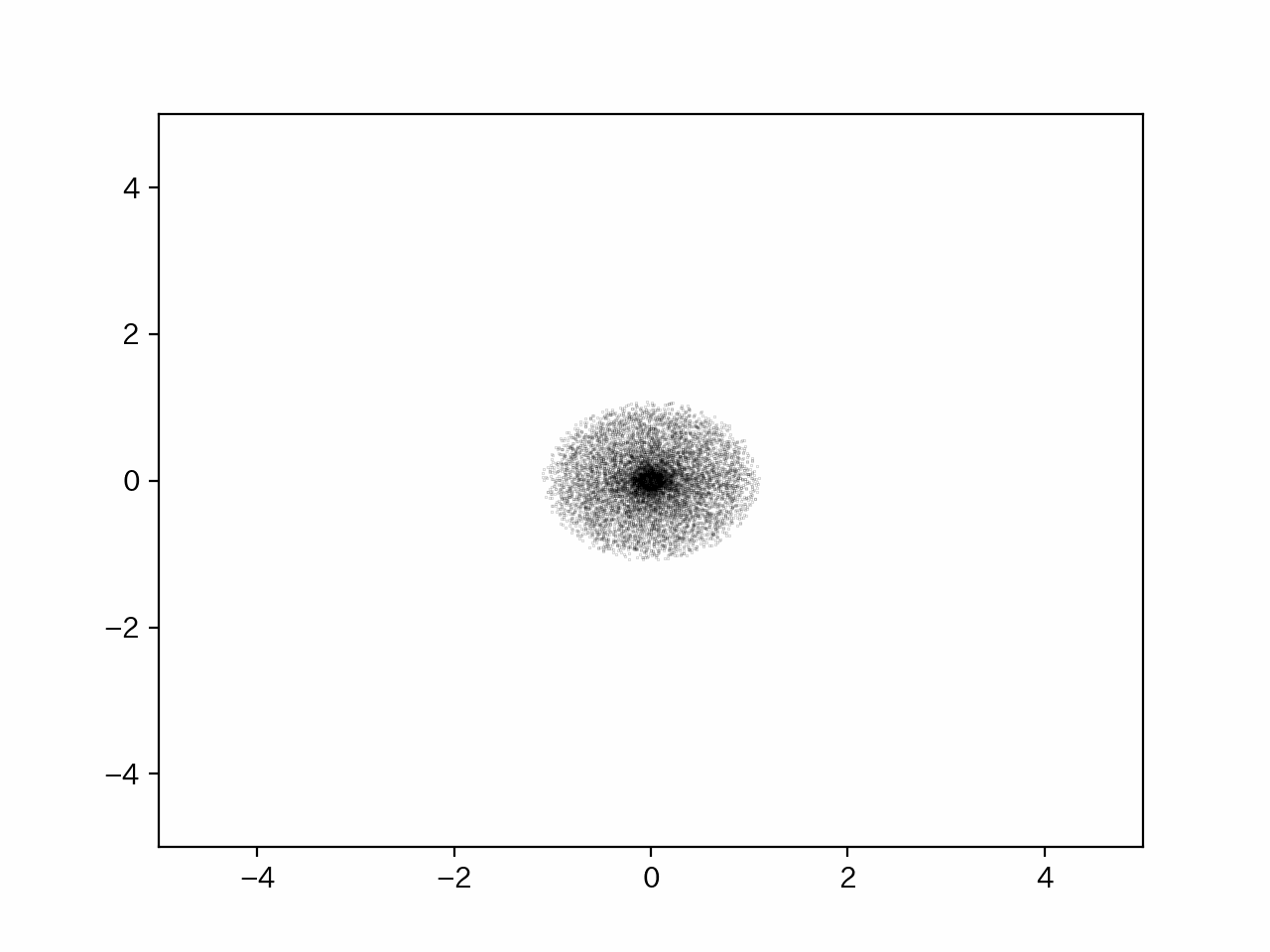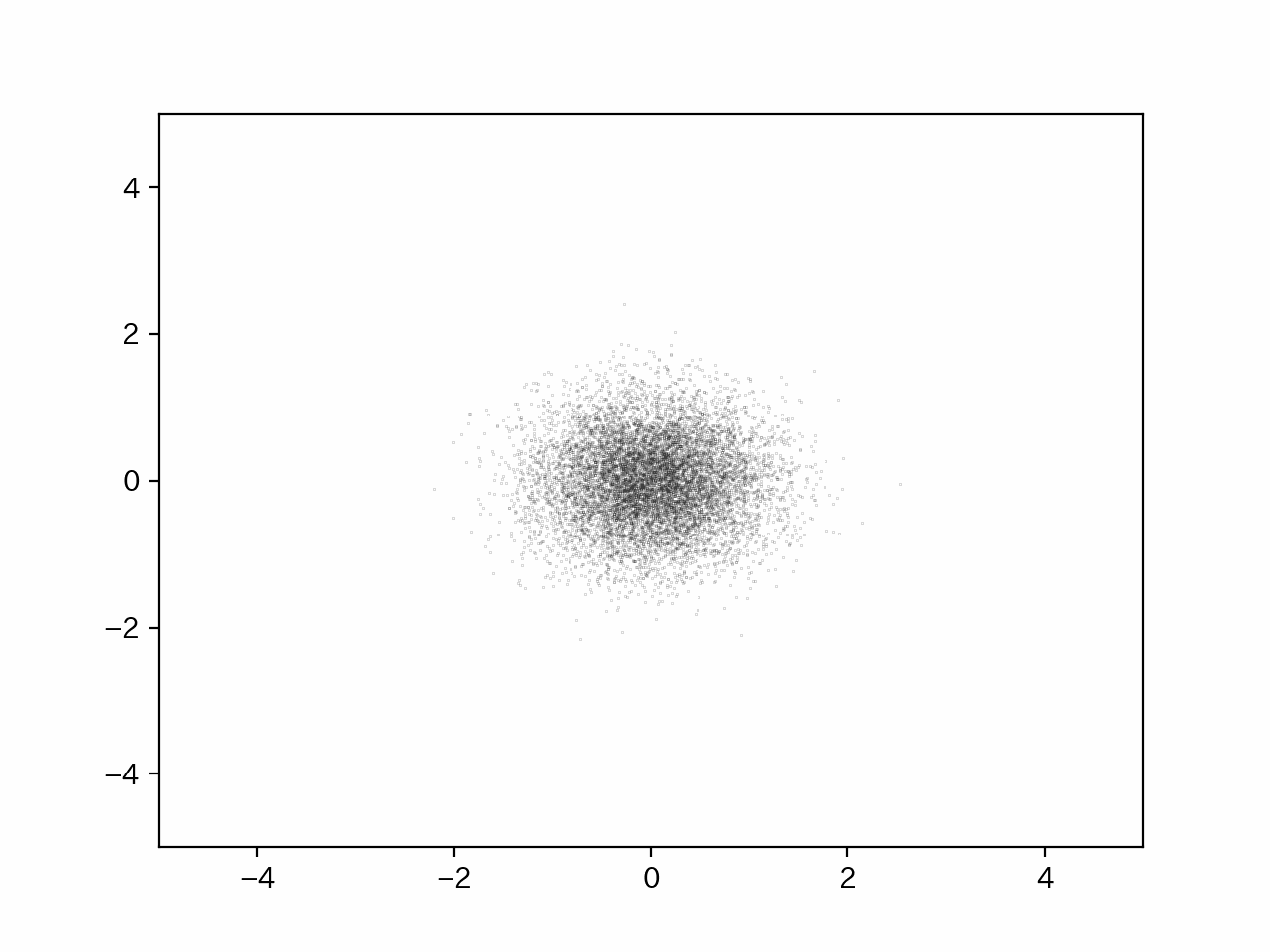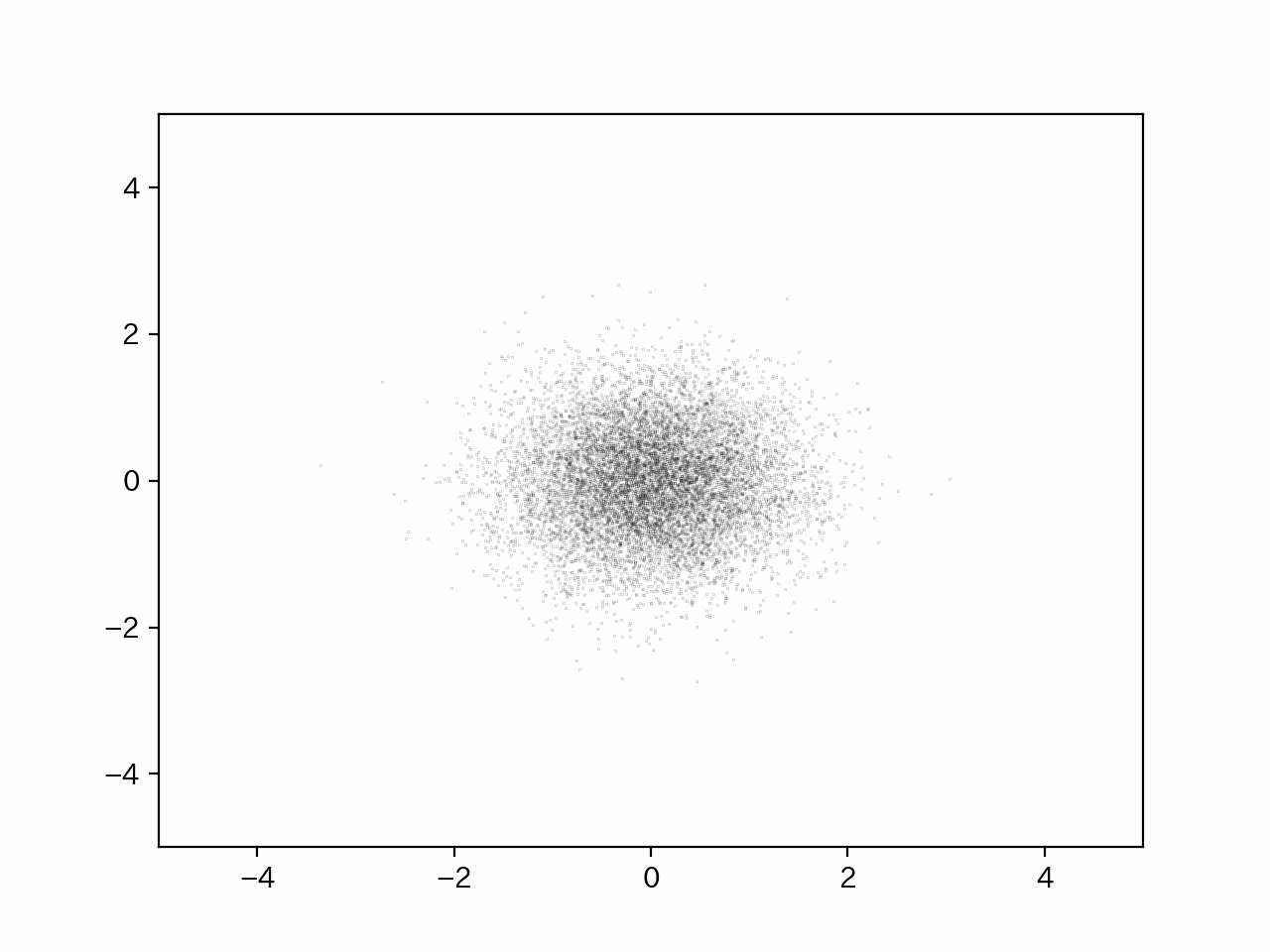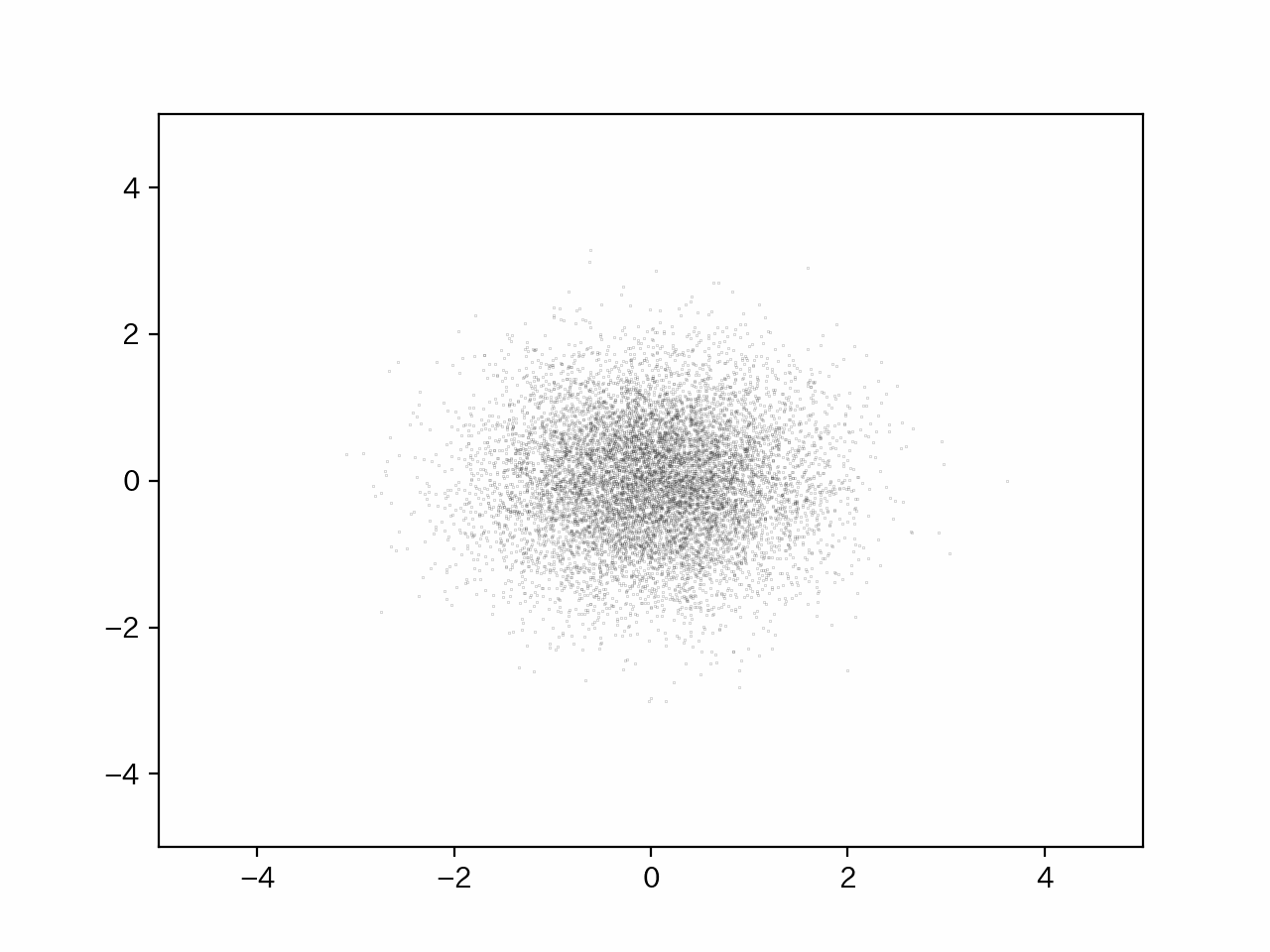
以下、シミュレーション結果の概略を示す。

このように、粒子自体の平均座標は常に0であるが、時間経過に対応する試行回数が増えるごとに、レアではあるが同じような方向に移動しまくり遠くまで行ける粒子が少しずつ増えていく。

したがって、溶媒は拡散されていき濃度は均一になっていく。

そのことに対する説明として、1次元のランダムウォークではあるが、以下のように考える。

粒子の存在位置は初期位置を原点（平均）とした場合、ある位置に粒子が存在する確率は、1回の試行確率$p=0.5$の2項分布に従う。したがって、試行回数nが増えるほど、分散である幅が大きくなる。

なので、少しずつではあるがより遠くへ行ける粒子数も増加していく。

導入

2次元空間で考える。原点を中心とする円である$x^2+y^2=r^2$内部に粒子が敷き詰められていると考える。それら粒子は、一定である微小時間ごとに360度全方向に対してランダムで一定距離だけ移動するものとする(2次元ランダムウォーク)。

プログラム

python random_walk.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
import random
import matplotlib.animation as animation
fig = plt.figure()
ims = []
L=5
plt.xlim(-L,L)
plt.ylim(-L,L)

N=100
n=100
r=np.linspace(0, 1, n)
theta = np.linspace(0, 2 * np.pi, n)

R,Theta= np.meshgrid(r, theta)
X = R * np.cos(Theta)
Y = R * np.sin(Theta)

r1=0.1
for l in range(N):
  for i in range(n):
    for k in range(n):
      theta1 = random.uniform(0, 2 * np.pi)
      X[i][k]=r1*math.cos(theta1)+ X[i][k]
      Y[i][k]=r1*math.sin(theta1)+ Y[i][k]
  im=plt.scatter(X, Y, color='black', s=0.01,marker=".")
  ims.append([im])
# 10枚のプロットを 100ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=100)
ani.save("Sample_random_walk.gif", writer = 'imagemagick')

結果

これを実行すると以下のような動画が出力される。

このように、時間が経つにしたがって、少しずつではあるが拡散していき、濃度は均一になっていくことが分かる。もちろん、粒子の平均位置は常に0ではあるが、あくまで平均なので遠くにいくレアな場合が存在することを頭に入れておく必要性がある。

考察

さて、拡散現象を説明するため、比較的簡単な1次元で考察する。

1次元ランダムウォークと2項分布

1次元ランダムウォークは原点を初期位置とした、2項分布で考えることができる。1回の試行で正方向に+1だけ行く確率と負方向に-1だけ進む確率は等しく$p=0.5$であるとする。

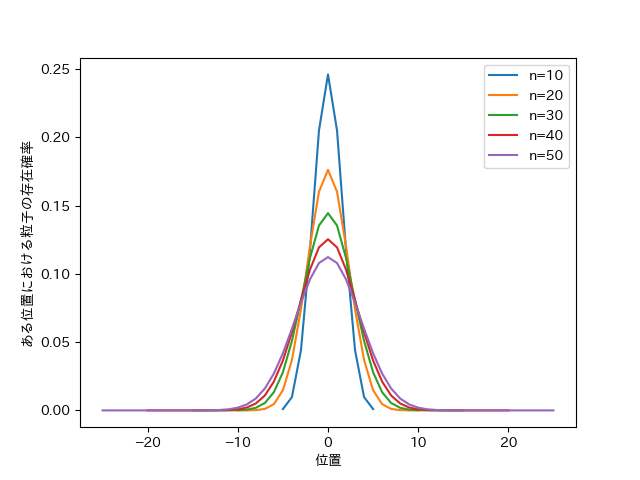
そこで、試行回数(10,20,30,40,50回)において粒子の存在確率は、以下のような2項分布で表される。

ただし、以下のプログラムを用いた。

python bi_p.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

p=0.5

def factorial(num):
  num2=1
  for i in range(1,num+1):
    #print(i)
    num2=num2*i
  return num2

def binomial_distribution(n):
  m=np.arange(0,n+1,1)
  #平均
  mu=n*p
  #F=0
  P_ary=[]
  #F_ary=[]
  for k in range(len(m)):
    #print(m[k])
    combi=factorial(n)/(factorial(m[k])*factorial(n-m[k]))
    P=combi*(p**(m[k])*(1-p)**(n-m[k]))
    #F=F+P
    P_ary.append(P)
    #F_ary.append(F)
  m2=m-mu
  plt.plot(m2,P_ary,label="n="+str(n))
  return m2, P_ary, 

binomial_distribution(10)
binomial_distribution(20)
binomial_distribution(30)
binomial_distribution(40)
binomial_distribution(50)

plt.legend()
plt.xlabel("位置")
plt.ylabel("ある位置における粒子の存在確率")
plt.savefig("ある位置における粒子の存在確率.png")
plt.show()

さて、グラフを見て分かるが、試行回数が増えるごとに、原点付近の存在確率が少しずつ低下していきその代わりに、原点から離れた地点の存在確率が極めてわずかではあるが増加していることが分かる。

このことから、時間が経つにつれてより遠くに行くことのできる粒子が増加していき、代わりに原点付近の粒子は少なくなっていく。

これが拡散現象の正体であると考えられる。

まとめ

今回は、統計力学のエントロピー増大の法則でよく考えられる拡散現象についてランダムウォークモデルを採用することで、説明することができるのか調査した。結果、原点付近の濃度は時間の経過とともに低下し、代わりに原点から離れた位置における濃度は上昇することが分かった。これはつまり、時間経過とともに、濃度が均一になっていくことを示している。

まとめ