はじめに
研究で高速に物体検出を行うためにSSD(Single Shot MultiBox Detector)を理解する必要がありました。
色々と情報を探してみたのですが、TensorFlowの実装例がとても少なく感じました。せっかく見つけた実装例もコメントや解説はほぼ皆無で、なにをやっているのかがとてもわかりにくいです(SSDが少々複雑な構造をもっているので)。
そもそも、SSDの説明自体がなかなか見つかりません。
そこで、いっそ自分で実装してしまおうと思い立った次第です。今回はそのための第一歩として、SSDの一部であるVGG16の実装を行いました。
対象者
- Pythonの基本がわかっている人
- ディープラーニングの基本がわかっている人(損失関数とかConvolutoinとかPoolingとか)
- CNNに興味がある人
環境
- Python 3.6.1 (3.6.2 is latest)
- TensorFlow
- Numpy
- skimage (読み込む画像によっては必要)
完成したものをGitHubにあげているので、ソースを見たい方はご覧ください。
VGG16の構成について
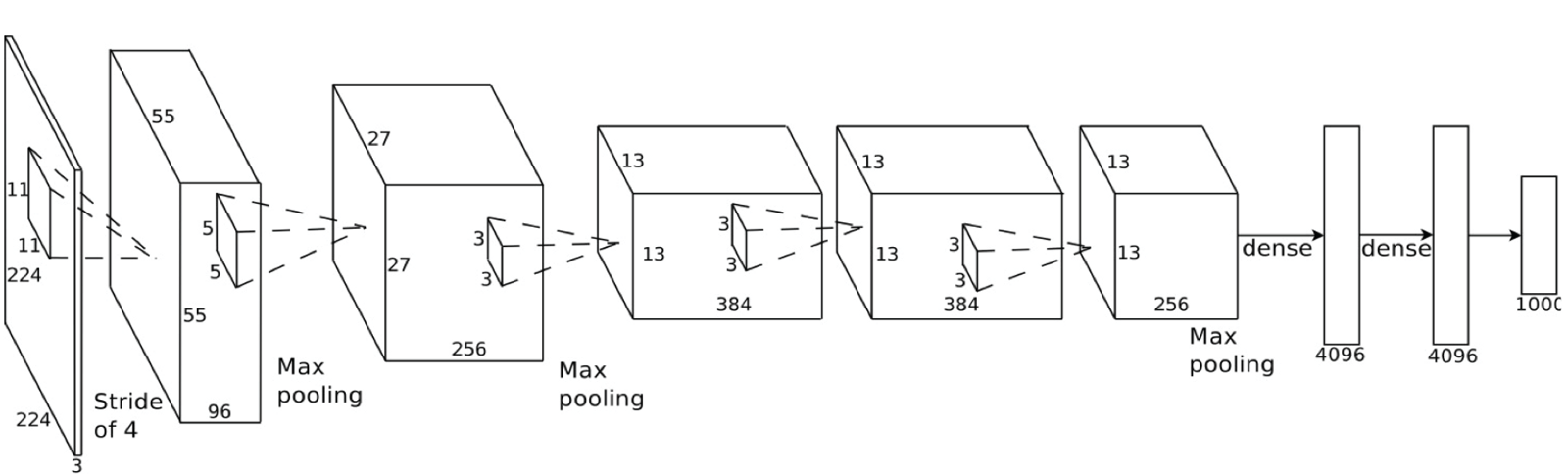
quoted from https://medium.com/@ageitgey/machine-learning-is-fun-part-3-deep-learning-and-convolutional-neural-networks-f40359318721
ネットワークの構成は下のようになっています。
| 層の種類 | 入力 | フィルター, 重み行列 |
|---|---|---|
| Convolution1_1 | $(224 \times 224 \times 3)$ | $(3 \times 3 \times 64)$ |
| Convolution1_2 | $(224 \times 224 \times 64)$ | $(3 \times 3 \times 64)$ |
| Max-Pooling1 | $(224 \times 224 \times 64)$ | $(2 \times 2 \times 64)$ |
| Convolution2_1 | $(112 \times 112 \times 64)$ | $(3 \times 3 \times 128)$ |
| Convolution2_2 | $(112 \times 112 \times 128)$ | $(3 \times 3 \times 128)$ |
| Max-Pooling2 | $(112 \times 112 \times 64)$ | $(2 \times 2 \times 128)$ |
| Convolution3_1 | $(56 \times 56 \times 128)$ | $(3 \times 3 \times 256)$ |
| Convolution3_2 | $(56 \times 56 \times 256)$ | $(3 \times 3 \times 256)$ |
| Convolution3_3 | $(56 \times 56 \times 256)$ | $(3 \times 3 \times 256)$ |
| Max-Pooling3 | $(56 \times 56 \times 256)$ | $(2 \times 2 \times 256)$ |
| Convolution4_1 | $(28 \times 28 \times 256)$ | $(3 \times 3 \times 512)$ |
| Convolution4_2 | $(28 \times 28 \times 512)$ | $(3 \times 3 \times 512)$ |
| Convolution4_3 | $(28 \times 28 \times 512)$ | $(3 \times 3 \times 512)$ |
| Max-Pooling4 | $(28 \times 28 \times 512)$ | $(2 \times 2 \times 512)$ |
| Convolution5_1 | $(14 \times 14 \times 256)$ | $(3 \times 3 \times 512)$ |
| Convolution5_2 | $(14 \times 14 \times 512)$ | $(3 \times 3 \times 512)$ |
| Convolution5_3 | $(14 \times 14 \times 512)$ | $(3 \times 3 \times 512)$ |
| Max-Pooling5 | $(14 \times 14 \times 512)$ | $(2 \times 2 \times 512)$ |
| Fully-Connection6 | $(7 \times 7 \times 512)$ | $(25,088 \times 4096)$ |
| Fully-Connection7 | $4096$ | $(4096 \times 4096)$ |
| Fully-Connection8 | $4096$ | $(4096 \times 1000)$ |
| Output | $1000$ |
VGG16では原則、Convolution層では($3 \times 3$)、Pooling層では($2 \times 2$)のフィルターを使いますが、チャネル数(奥行き)があるので$3$次元で表現されています。ストライドは、畳込みは$1$、プーリングは$2$で統一されています。入力次元についてはこちらを参考にさせていただきました。ここでの表記の形式としては、
- 入力: (入力画像の高さ $\times$ 入力画像の幅 $\times$ 入力画像のチャネル数)
- フィルター: (フィルターの高さ $\times$ フィルターの幅 $\times$ 出力画像のチャネル数)
としています。複数層(チャネル数が大きい場合)での畳込みがイメージしにくい方は、こちらが参考になります。
実装
VGG16はすべての層が直列結合なので、とてもシンプルです。実装に必要な情報も、上記の入力とフィルター、ストライドでほぼすべてです。あとはTensorFlowでそれらをどう表現するかが問題となります。
TensorFlowの基礎
TensorFlowの使い方は、とても詳しく解説している方がいらっしゃるので紹介させていただきます。TensorFlowの基礎
畳み込み、プーリングのための関数を定義する
TensorFlowのプレースホルダーとグラフセッションが理解できたら、次はどのように畳み込みやプーリングを表現するかです。TensorFlowでは、次のようにして畳み込み層やプーリング層を作成(連結)します。
# ストライド1の畳み込み層の作成
# filter: [(filterの高さ) x (filterの幅) x (入力チャネル数) x (出力チャネル数)]
# strides: [1 x (上下stride幅) x (左右stride幅) x 1]
# padding: SAMEを指定すると畳込み前に0パディングをするので、入出力で画像サイズが変化しない
tf.nn.conv2d(input, filter, strides=[1, 1, 1, 1], padding='SAME')
# ストライド2のマックスプーリング層の作成
# ksize: [1 x (kernelの高さ) x (kernelの幅) x 1]
# strides: [1 x (上下stride幅) x (左右stride幅) x 1]
# padding: SAMEを指定するとプーリング前に0パディングをするので、出力サイズは入力サイズの1/2になる。(切り上げ)
tf.nn.max_pool(input, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
このように、プーリング層の引数はVGG16においては常に同じ値を用いるのでとても簡潔に書くことができますが、畳み込み層については層ごとにフィルターのサイズを変えたり、重みを初期化する必要があるため、そのための処理を関数として抽出しておきたいと思います。これがSSD300の実装で効いてきます。
def convolution(input, name):
"""
Args: output of just before layer
Return: convolution layer
"""
with tf.variable_scope(name):
size = vgg.structure[name]
kernel = get_weight(size[0], name='w_'+name)
bias = get_bias(size[1], name='b_'+name)
conv = tf.nn.conv2d(input, kernel, strides=vgg.conv_strides, padding='SAME', name=name)
out = tf.nn.relu(tf.add(conv, bias))
return out
def pooling(input, name):
"""
Args: output of just before layer
Return: max_pooling layer
"""
return tf.nn.max_pool(input, ksize=vgg.ksize, strides=vgg.pool_strides, padding='SAME', name=name)
def get_weight(shape, name):
"""
generate weight tensor
Args: weight size
Return: initialized weight tensor
"""
initial = tf.truncated_normal(shape, 0.0, 1.0) * 0.01
return tf.Variable(initial, name='w_'+name)
def get_bias(shape, name):
"""
generate bias tensor
Args: bias size
Return: initialized bias tensor
"""
return tf.Variable(tf.truncated_normal(shape, 0.0, 1.0) * 0.01, name='b_'+name)
ここで、nameには各層の名前を与えます(e.g. name='conv1_1')。そして予めこれらの名前に対応するフィルターの準備を行っておきます。
"""
size-format:
[ [ convolution_kernel ], [ bias ] ]
[ [ f_h, f_w, in_size, out_size ], [ out_size ] ]
"""
structure = {
# convolution layer 1
'conv1_1': [[3, 3, 3, 64], [64]],
'conv1_2': [[3, 3, 64, 64], [64]],
# convolution layer 2
'conv2_1': [[3, 3, 64, 128], [128]],
'conv2_2': [[3, 3, 128, 128], [128]],
...
}
このように、複雑なCNNの重みやバイアスの初期化を別の関数に抽出しておくと、実際にネットワークをビルドするときにとても簡潔に書けます。最後に、全結合層を実装します。上記の表で、Fully-Connection6を例に考えてみます。入力は($7 \times 7 \times 512$)なので、ニューロンの数は全てで$7 \times 7 \times 512 = 25,088$となります。これらを全結合し出力のサイズを$4096$にする必要があるので、ラスタライズした入力に対して($25,088 \times 4096$)の重み行列を掛ければいいことになります。これを実際にコードで書くと、次のようになります。
def fully_connection(input, activation, name):
"""
Args: output of just before layer
Return: fully_connected layer
"""
size = vgg.structure[name]
with tf.variable_scope(name):
shape = input.get_shape().as_list()
dim = reduce(lambda x, y: x * y, shape[1:])
x = tf.reshape(input, [-1, dim])
weights = get_weight([dim, size[0][0]], name=name)
biases = get_bias(size[1], name=name)
fc = tf.nn.bias_add(tf.matmul(x, weights), biases)
fc = activation(fc)
return fc
以上でVGG16を実装するための準備が整いました。
それでは、上記で定義した関数やパラメータを用いて、実際にVGG16をビルドしてみます。
class VGG16:
...
def build(self, input, is_training=True):
"""
input is the placeholder of tensorflow
build() assembles vgg16 network
"""
# flag: is_training? for tensorflow-graph
self.train_phase = tf.constant(is_training) if is_training else None
self.conv1_1 = self.convolution(input, 'conv1_1')
self.conv1_2 = self.convolution(self.conv1_1, 'conv1_2')
self.pool1 = self.pooling(self.conv1_2, 'pool1')
self.conv2_1 = self.convolution(self.pool1, 'conv2_1')
self.conv2_2 = self.convolution(self.conv2_1, 'conv2_2')
self.pool2 = self.pooling(self.conv2_2, 'pool2')
self.conv3_1 = self.convolution(self.pool2, 'conv3_1')
self.conv3_2 = self.convolution(self.conv3_1, 'conv3_2')
self.conv3_3 = self.convolution(self.conv3_2, 'conv3_3')
self.pool3 = self.pooling(self.conv3_3, 'pool3')
self.conv4_1 = self.convolution(self.pool3, 'conv4_1')
self.conv4_2 = self.convolution(self.conv4_1, 'conv4_2')
self.conv4_3 = self.convolution(self.conv4_2, 'conv4_3')
self.pool4 = self.pooling(self.conv4_3, 'pool4')
self.conv5_1 = self.convolution(self.pool4, 'conv5_1')
self.conv5_2 = self.convolution(self.conv5_1, 'conv5_2')
self.conv5_3 = self.convolution(self.conv5_2, 'conv5_3')
self.pool5 = self.pooling(self.conv5_3, 'pool5')
self.fc6 = self.fully_connection(self.pool5, Activation.relu, 'cifar')
self.fc7 = self.fully_connection(self.fc6, Activation.relu, 'fc7')
self.fc8 = self.fully_connection(self.fc7, Activation.softmax, 'fc8')
self.prob = self.fc6
return self.prob
...
(convolution(), pooling(), fully_connection()などはVGG16クラスに移動してあります。)
学習
-
学習データについて
例として、cifar-10の分類問題を扱ってみます。ここで注意すべきなのは、学習に用いる画像のサイズについてです。プーリングの度に画像サイズが半分になるので、$5$回プーリング層を経由するVGG16では画像サイズはin_size$\times 2^{-5}$となります。
用いる画像がもともと小さいもの(MNISTは($28 \times 28$))の場合は途中で画像サイズが($1 \times 1$)となり、点になってしまいます。これでは学習が上手く行かないので、VGG16に少し手を加える必要があります。具体的には、$5$回目のプーリングをスキップするなどの方法を用います。cifar-10は($32 \times 32$)で、最終出力が($1 \times 1$)となるだけなので、ギリギリセーフです。
ただ、($32 \times 32$)を入力として与えた場合全結合層にて$512$のニューロンが得られるので、これを$1000$に膨張させることはしません。cifar-10特別仕様として全結合層は$1$つに変更し、その重み行列の型を($ 512 \times 512$)とします。つまり、入出力前後でサイズが変わらないようにします。 -
学習方法
変更後のVGG16の出力はサイズが$512$なので、10クラスに分類するためには($512 \times 10$)の重み行列を掛けてやる必要があります。まずは入力のプレースホルダーと重み行列、バイアスの準備から始めます。
# input image's placeholder and output of VGG16
input = tf.placeholder(shape=[None, 32, 32, 3], dtype=tf.float32)
# params for converting to answer-label-size
w = tf.Variable(tf.truncated_normal([512, 10], 0.0, 1.0) * 0.01, name='w_last')
b = tf.Variable(tf.truncated_normal([10], 0.0, 1.0) * 0.01, name='b_last')
次に、ビルドしたVGG16の出力に対して、準備した重み行列とバイアスの演算を組み合わせます。
活性化関数はソフトマックス関数です。
fmap = vgg.build(input, is_training=True)
predict = tf.nn.softmax(tf.add(tf.matmul(fmap, w), b))
最後に、教師データのプレースホルダーを作成し、損失関数を定義します。
# params for defining Loss-func and Training-step
ans = tf.placeholder(shape=None, dtype=tf.float32)
ans = tf.squeeze(tf.cast(ans, tf.float32))
# cross-entropy
loss = tf.reduce_mean(-tf.reduce_sum(ans * tf.log(predict), reduction_indices=[1]))
optimizer = tf.train.GradientDescentOptimizer(0.05)
train_step = optimizer.minimize(loss)
後は、ひたすら学習させるのみです。
...
with tf.Session() as sess:
# Training-loop
lossbox = []
for e in range(EPOCH):
for b in range(int(DATASET_NUM/BATCH)):
batch, actuals = get_next_batch(len(train_labels))
sess.run(train_step, feed_dict={input: batch, ans: actuals})
print('Batch: %3d' % int(b+1)+', \tLoss: '+str(sess.run(loss, feed_dict={input: batch, ans: actuals})))
if (b+1) % 100 == 0:
print('============================================')
print('START TEST')
test()
print('END TEST')
print('============================================')
time.sleep(0)
lossbox.append(sess.run(loss, feed_dict={input: batch, ans: actuals}))
print('========== Epoch: '+str(e+1)+' END ==========')
...
おわりに
今回はcifar-10を学習させましたが、自前で準備したデータセットを読み込む場合、画像の値を[0, 255]から[0, 1]に正規化する必要がありますが、これにはutil/util.pyに画像読み込み関数を準備していますので、そちらを利用していただくと正規化された画像を読み込むことができます。
次はSSD編を書きますが、実装自体は既にほぼ完了しているので、気になる方は見てみてください。間違ってたら教えてください。
できるだけ早くSSD編も書き上げたいと思います。
SSD300の実装
参考
https://medium.com/@ageitgey/machine-learning-is-fun-part-3-deep-learning-and-convolutional-neural-networks-f40359318721
https://qiita.com/mizti/items/5e50c1367b95b027828f
https://qiita.com/nvtomo1029/items/601af18f82d8ffab551e
https://qiita.com/rindai87/items/4b6f985c0583772a2e21