◆前章:Part4 学習に関するテクニック
◆目次:ディープラーニングを基本から学ぶ
■5.畳み込みニューラルネットワーク
畳み込みニューラルネットワーク(convolutional neural network : CNN )は、特に画像認識のディープランニングの手法のほとんどすべてがベースとしていると言われるほど、ディープランニングに欠かせない手法である。
▼5.1.CNNの構造
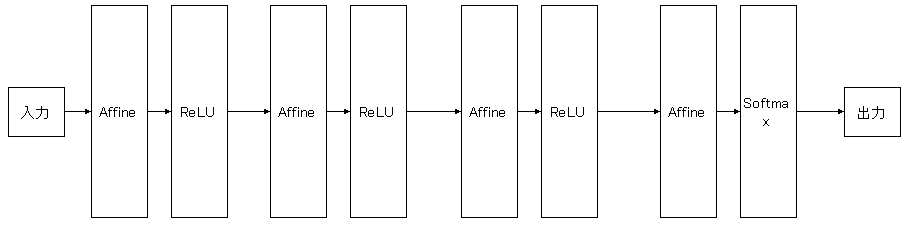
これまでの章で出てきた上記のようなニューラルネットワークは全結合と呼ばれ、全結合層(Affineレイヤ)と活性化関数レイヤ(ReLu、Sigmoid)の組み合わせを層数分重ね、最後にSoftmaxレイヤで結果を出力する。
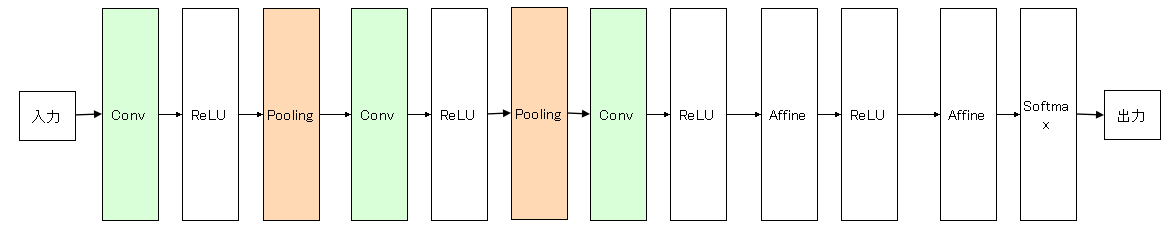
一方で、CNNでは全結合層で使われるレイヤに加えて、ConvolutionレイヤとPoolingレイヤが加わる。(Poolingレイヤは省略されることがある)
全結合層では、入力データの形状が無視されてしまうという問題がある。
例えば画像データの場合、28ピクセル×28ピクセルの入力画像があった場合に、全結合層ではそれを一列に並べて784個のデータとして扱われる。
画像データの元の形状(28ピクセル×28ピクセル)には汲み取るべき本質的なパターンが潜んでいる可能性があり、それを一列に並べて扱うことで、その本質を見落としてしまう。
CNNでは、畳み込み層(Convolutionレイヤ)で形状を維持するため、画像などの形状を有したデータを正しく理解できる可能性が高まる。
▼5.2.畳み込み層(Convolutionレイヤ)
▽5.2.1.畳み込み演算
畳み込み層で行う処理のことを言い、画像処理でのフィルター演算に相当する。
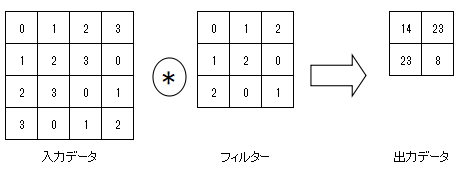
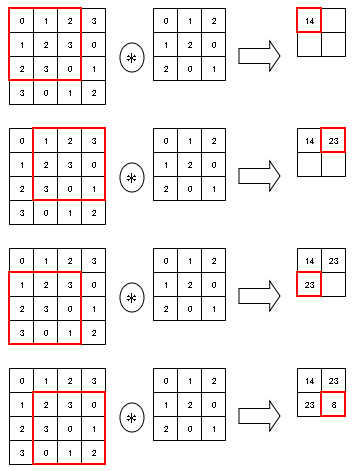
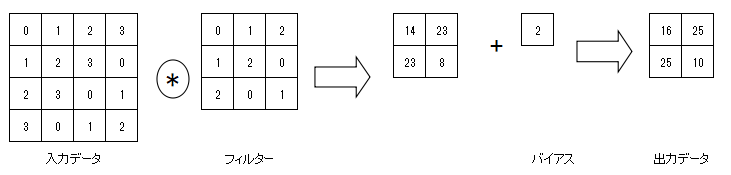
畳み込み演算は、入力データに対してフィルターを一定の間隔でスライドさせながら適用する。
入力データの対応する要素とフィルターの要素を乗算し、その和を求める。
この計算方式は積和演算と呼ばれる。
CNNでは、この入力データとフィルターの乗算に加えて、バイアスの加算が存在する。
バイアスはフィルター適用後のデータに加算される。
バイアスの値は1つだけであり、同じ値がフィルター適用後のすべての要素に加算される。
▽5.2.2.パディング、ストライドで出力サイズを調整する
パディング
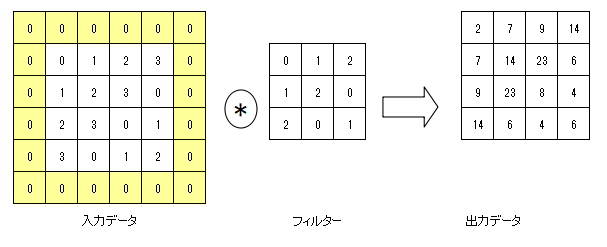
出力サイズを調整するため、畳み込み層の処理を行う前に、入力データの周囲に例えば0などの固定のデータを埋めることをパディングと言う。
上記の例では(4, 4)のサイズの入力データに対して、幅1のパディング(網掛けの部分)を適用している。
入力データが(4, 4)のサイズに(3, 3)のフィルターを適用すると、出力サイズは(2, 2)となるが、幅1のパディングを適用することで出力サイズは(4, 4)となる。
ストライド
フィルターを適用する間隔をストライドと言う。
これまでの例では、ストライドはすべて1であったが、それ以外のストライドも適用可能である。
ストライドを大きくすると出力サイズは小さくなる。
出力サイズの計算式
OH = {\frac{H + 2P -FH}{S}} + 1
\\
OW = {\frac{W + 2P -FW}{S}} + 1
※
$入力サイズ:(H, W)、フィルターサイズ:(FH, FW)、出力サイズ:(OH, OW)、パディング:P、ストライド:S$
出力サイズが割り切れない場合にエラーを出力するなど対応する必要がある。
ディープラーニングのフレームワークによっては、エラーとせず丸め処理を行って先に進むような実装をしているものもある。
▽5.2.3.畳み込み演算を3次元データに適用する
これまでの例では縦方向と横方向の2次元の形状を対象としたものであったが、画像の場合は縦・横に加えてチャンネル方向も合わせた3次元のデータを扱う必要がある。
ここで言うチャンネルは、画像のカラーモードで決まるもので、例えばRGB画像ではチャンネル数は3となる。
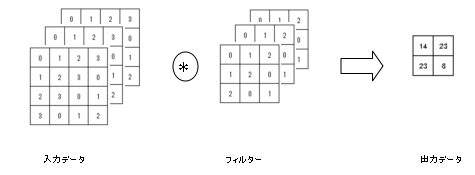
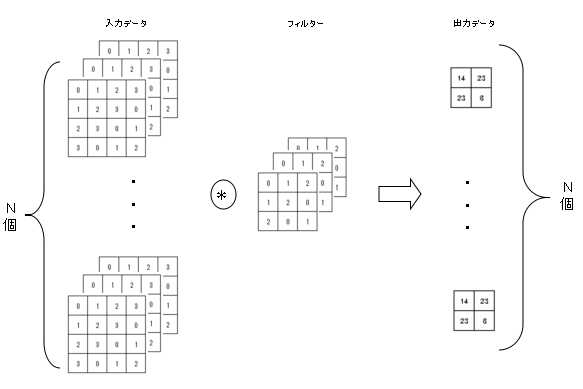
上記は3チャンネルのデータの場合の畳み込み演算の計算イメージ。
チャンネルごとに入力データフィルターの畳み込み演算を行い、チャンネルごとの結果を加算してひとつの出力を得る。
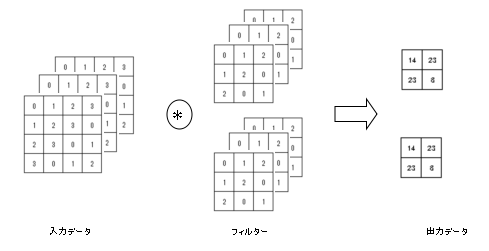
出力を複数にしたい場合は、フィルターを複数組用意する。
▽5.2.4.畳み込み演算をバッチ処理に対応させる
これまでの章で出てきた全結合と同じように畳み込み演算でもバッチ処理に対応することができる。
バッチ処理に対応させる場合、入力データは3次元のデータをバッチ数分持つことになるので4次元のデータとなる。
▼5.3.プーリング層(Poolingレイヤ)
▽5.3.1.プーリング層の仕組み
プーリングとは、縦・横方向の空間を小さくする演算である。
具体的には、ある一定の領域をひとつの要素に集約する処理を行い、空間サイズを小さくする。
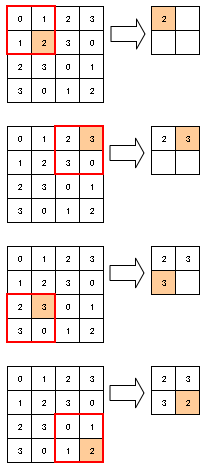
上記は、Maxプーリングを領域2×2、ストライド2で行った場合の処理手順である。
Maxプーリングとはある一定の領域で最大値を取る演算。
他に平均を取るAverageプーリングがある。
プーリングを適用する領域サイズとストライドには同じ値を設定するのが一般的であるようだ。
▼5.4.CNNの実装
▽5.4.1.im2colという展開方式を実装する
”im2col”とは、ディープラーニングのフレームワークで用いられる関数の名前であり、畳み込み演算の実装を、計算しやすい行列の計算に帰着させることを目的としている。
具体的には行列を2次元に変換するのが”im2col”の役割である。
# coding: utf-8
import numpy as np
# im2colの実装
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : (データ数, チャンネル, 高さ, 幅)の4次元配列からなる入力データ
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
Returns
-------
col : 2次元配列
"""
"""
N : 入力データ数
C : 入力チャネル数
H : 入力高さ
W : 入力幅
"""
N, C, H, W = input_data.shape
# 出力高さを計算
out_h = (H + 2*pad - filter_h)//stride + 1
# 出力幅を計算
out_w = (W + 2*pad - filter_w)//stride + 1
# 入力データ(高さ、幅部分)にパディング(0埋め)を適用する
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
# 出力データの初期化
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
# 出力データをセットしていく
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
# 出力データに入力データ(高さ、幅部分)をセットしていく
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
"""
出力データを転置
(データ数, チャンネル, フィルターの高さ, フィルターの幅, 出力高さ, 出力幅)
→(データ数, 出力高さ, 出力幅, チャンネル, フィルターの高さ, フィルターの幅)
転置後のデータを2次元の行列に変換する
1次元目の要素数: データ数×出力高さ×出力幅
2次元目の要素数: 転置後のデータと1次元目の要素数から設定される
"""
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
# col2imの実装
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col : 出力データ(2次元配列)
input_shape : 入力データの形状(例:(10, 1, 28, 28))
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
Returns
-------
img : 入力データ
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
# 出力データの形状を入力データの形状に戻す
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
# 入力データを初期化
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
# 出力データを入力データにセットしていく
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
# パディングを除いて返す
return img[:, :, pad:H + pad, pad:W + pad]
”im2col”と、それと逆のことを行う”col2im”の実装。
”col2im”は逆伝播で用いられる。
▽5.4.2.畳み込み層(Convolutionレイヤ)の実装
畳み込み層(Convolutionレイヤ)の実装では、順伝播では”im2col”を使い、2次元配列に展開してから順伝播の計算を行い、計算後の結果を入力データから見て適切な形状にしている。
逆伝播では最初に逆伝播の計算を行ってから、"col2im"を使い、計算後の結果を2次元配列から適切な形状に展開している。
# coding: utf-8
import numpy as np
# 畳み込み層(Convolutionレイヤ)の実装
class Convolution:
"""
Parameters:
W : フィルター(重み)
b : バイアス
stride : ストライド(省略時=1)
pad : パディング(省略時=0)
"""
# 初期化
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# 重み・バイアスパラメータの勾配
self.dW = None
self.db = None
# 順伝播
def forward(self, x):
# フィルターの個数:FN、チャネル数:C、高さ:FH、幅:FWを取得
FN, C, FH, FW = self.W.shape
# 入力データの個数:N、チャネル数:C、高さ:H、幅:Wを取得
N, C, H, W = x.shape
# 出力高さ、幅を取得
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
# 入力データを2次元配列に展開
col = im2col(x, FH, FW, self.stride, self.pad)
# フィルターを2次元配列に展開
col_W = self.W.reshape(FN, -1).T
# 出力値(=次層への伝達値)を求める
out = np.dot(col, col_W) + self.b
# 出力値を適切な形状にする
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
# 入力データを保持しておく
self.x = x
# 入力データ(2次元配列の形状)を保持しておく
self.col = col
# フィルター(2次元配列の形状)を保持しておく
self.col_W = col_W
return out
# 逆伝播
def backward(self, dout):
# フィルターの個数:FN、チャネル数:C、高さ:FH、幅:FWを取得
FN, C, FH, FW = self.W.shape
# (逆伝播の)入力データを2次元配列に展開
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
# バイアスの勾配値を求める
self.db = np.sum(dout, axis=0)
# フィルターの勾配値を求めて、形状を元に戻す
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
# (逆伝播の)出力データを求め、形状を元に戻す
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
▽5.4.3.プーリング層(Poolingレイヤ)の実装
Poolingレイヤの実装は、3段階の流れで行われる。
1.入力データを展開する
2.行ごとに最大値を求める
3.適切なサイズに整形する
# coding: utf-8
import numpy as np
# プーリング層(Poolingレイヤ)の実装
class Pooling:
# 初期化
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
# 順伝播
def forward(self, x):
# 入力データの個数:N、チャネル数:C、高さ:H、幅:Wを取得
N, C, H, W = x.shape
# 出力高さ、幅を取得
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# 入力データを2次元配列に展開
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
# 行ごとの最大値を求める
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
# 出力値を適切な形状にする
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
# 入力データを保持しておく
self.x = x
# 行ごとの最大値を保持しておく
self.arg_max = arg_max
return out
# 逆伝播
def backward(self, dout):
# (逆伝播の)入力データを並び変える
dout = dout.transpose(0, 2, 3, 1)
# 行ごとの最大値を求める
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
# (逆伝播の)出力データを求め、形状を元に戻す
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
▽5.4.4.CNNの実装
先に実装を示した畳み込み層(Convolutionレイヤ)とプーリング層(Poolingレイヤ)を組み合わせたCNNを実装する。
ネットワークの構成を
Convolution - ReLU - Pooling - Affine - ReLU - Affine - softmax
としたシンプルなCNNである。
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import pickle
import numpy as np
from collections import OrderedDict
class SimpleConvNet:
"""単純なConvNet
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 入力サイズ
hidden_size_list : 隠れ層のニューロンの数のリスト(e.g. [100, 100, 100])
output_size : 出力サイズ
activation : 活性化関数を指定 'relu' or 'sigmoid'
weight_init_std : 重みの標準偏差を指定(e.g. 0.01)
'relu'または'he'を指定した場合は「Heの初期値」を設定
'sigmoid'または'xavier'を指定した場合は「Xavierの初期値」を設定
"""
# 初期化
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
"""
input_dim : 入力データの次元(チャンネル、高さ、幅)
conv_param : Convolution層のハイパーパラメーターディクショナリ
- filter_num : フィルターの数
- filter_size : フィルターのサイズ
- pad : パディング
- stride : ストライド
hidden_size : 隠れ層(全結合)のニューロンの数
output_size : 出力層(全結合)のニューロンの数
weight_init_std : 初期化の際の重みの標準偏差
"""
# Convolution層のハイパーパラメーターをセット
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 重み、バイアスの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict() # 順序付きディクショナリ
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
# 認識(推論)を行う
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# 損失関数の値を求める
# x:入力データ, t:教師データ
def loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
# 認識精度を求める
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
# 重みパラメータに対する勾配を求める(誤差逆伝搬法)
# x:入力データ, t:教師データ
def gradient(self, x, t):
"""
Returns
-------
各層の勾配を持ったディクショナリ変数
grads['W1']、grads['W2']、...は各層の重み
grads['b1']、grads['b2']、...は各層のバイアス
"""
# forward(順伝播)
self.loss(x, t)
# backward(逆伝播)
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 求められた勾配値を設定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
# パラメータ(重み、バイアス)をファイルに保存する
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
# ファイルからパラメータ(重み、バイアス)をロードする
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
Part3で示した誤差逆伝播法で実装した2層ニューラルネットワークに、Convolution - ReLU - Poolingが加わったイメージとなる。