LoginSignup
2
1

More than 5 years have passed since last update.

@aokikenichi(青木 健一)

『経済・ファイナンスデータの計量時系列分析』章末問題をRで解く－第2章ARMA過程－

Last updated at Posted at 2016-11-06

『経済・ファイナンスデータの計量時系列分析』

の章末問題で「コンピュータを用いて」とあるものをRで解いています。
* サポートサイト（データダウンロード）

2.5

  • (1)
library(forecast)

data<-read.table("economicdata.txt",header=T)
ar4<-Arima(diff(log(data$indprod))*100, order=c(4, 0, 0))
ma3<-Arima(diff(log(data$indprod))*100, order=c(0, 0, 3))
arma1_1<-Arima(diff(log(data$indprod))*100, order=c(1, 0, 1))
arma2_1<-Arima(diff(log(data$indprod))*100, order=c(2, 0, 1))
arma1_2<-Arima(diff(log(data$indprod))*100, order=c(1, 0, 2))
arma2_2<-Arima(diff(log(data$indprod))*100, order=c(2, 0, 2))

name<-c('AR(4)', 'MA(3)', 'ARMA(1,1)', 'ARMA(2,1)', 'ARMA(1,2)', 'ARMA(2,2)')
aic<-c(
  AIC(ar4)/length(data$indprod),
  AIC(ma3)/length(data$indprod),
  AIC(arma1_1)/length(data$indprod),
  AIC(arma2_1)/length(data$indprod),
  AIC(arma1_2)/length(data$indprod),
  AIC(arma2_2)/length(data$indprod)
)
bic<-c(
  BIC(ar4)/length(data$indprod),
  BIC(ma3)/length(data$indprod),
  BIC(arma1_1)/length(data$indprod),
  BIC(arma2_1)/length(data$indprod),
  BIC(arma1_2)/length(data$indprod),
  BIC(arma2_2)/length(data$indprod)
)
out<-data.frame(matrix(aic, nrow=1))
out<-rbind(out, bic)
colnames(out)<-name
rownames(out)<-c('AIC', 'SIC')
out

       AR(4)    MA(3) ARMA(1,1) ARMA(2,1) ARMA(1,2) ARMA(2,2)
AIC 3.232032 3.239599  3.324956  3.277746  3.233284  3.246579
SIC 3.296225 3.293094  3.367752  3.331241  3.286779  3.310772

## figure
par(mfrow = c(2, 2))
par(mar = c(2, 2, 1, 1))
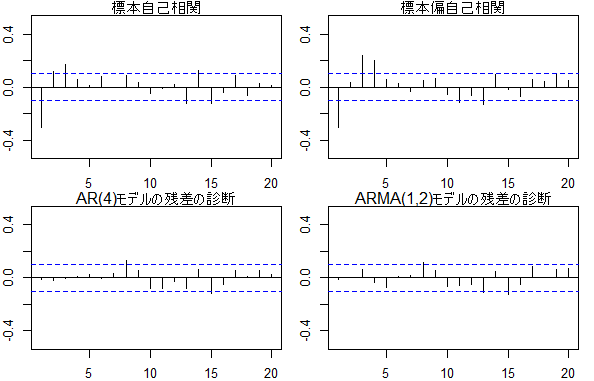
acf(diff(log(data$indprod)), xlim=c(1, 20), ylim=c(-0.5, 0.5))
mtext(text = '標本自己相関', side = 3)
pacf(diff(log(data$indprod)), xlim=c(1, 20), ylim=c(-0.5, 0.5))
mtext(text = '標本偏自己相関')
acf(ar4$residuals, xlim=c(1, 20), ylim=c(-0.5, 0.5))
mtext(text = 'AR(4)モデルの残差の診断', side = 3)
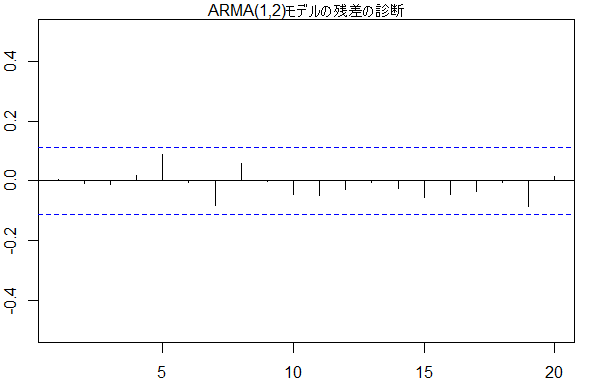
acf(arma1_2$residuals, xlim=c(1, 20), ylim=c(-0.5, 0.5))
mtext(text = 'ARMA(1,2)モデルの残差の診断', side = 3)

1_2.5.1.png

  • (2)
library(forecast)

data<-read.table("economicdata.txt",header=T)
ar4<-Arima(diff(log(data$indprod))*100, order=c(4, 0, 0))
arma1_2<-Arima(diff(log(data$indprod))*100, order=c(1, 0, 2))

AR(4)

Box.test(ar4$residuals[1:10], type="Ljung")

    Box-Ljung test

data:  ar4$residuals[1:10]
X-squared = 0.37762, df = 1, p-value = 0.5389

p>0.05より帰無仮説を棄却できないので自己相関があるとは言えない。

ARMA(1, 2)

Box.test(arma1_2$residuals[1:10], type="Ljung")

    Box-Ljung test

data:  arma1_2$residuals[1:10]
X-squared = 0.37971, df = 1, p-value = 0.5378

p>0.05より帰無仮説を棄却できないので自己相関があるとは言えない。

2.6

library(forecast)
data<-read.table("arma.txt", header=T)
  • (1)
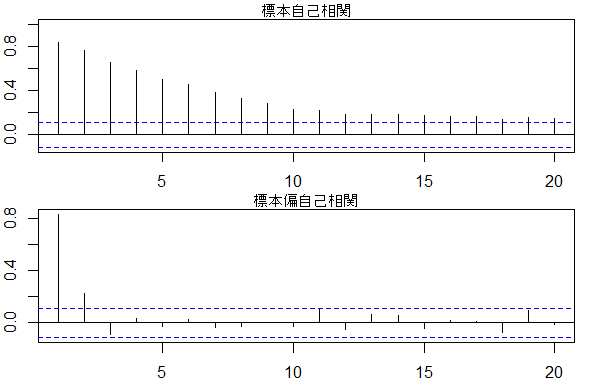
par(mfrow=c(2, 1))
acf(data$y1, xlim=c(1, 20))
mtext('標本自己相関', side = 3)
pacf(data$y1, xlim=c(1, 20))
mtext('標本偏自己相関', side = 3)

1_2.6.1.png

  • (2), (3)
###AR(2)
###ARMA(1,1),ARMA(2,1),ARMA(1,2),ARMA(2,2)
ar2<-Arima(data$y1, order=c(2, 0, 0))
arma1_1<-Arima(data$y1, order=c(1, 0, 1))
arma2_1<-Arima(data$y1, order=c(2, 0, 1))
arma1_2<-Arima(data$y1, order=c(1, 0, 2))
arma2_2<-Arima(data$y1, order=c(2, 0, 2))

name<-c('AR(2)', 'ARMA(1,1)', 'ARMA(2,1)', 'ARMA(1,2)', 'ARMA(2,2)')
aic<-c(
  AIC(ar2)/length(data$y1),
  AIC(arma1_1)/length(data$y1),
  AIC(arma2_1)/length(data$y1),
  AIC(arma1_2)/length(data$y1),
  AIC(arma2_2)/length(data$y1)
)
bic<-c(
  BIC(ar2)/length(data$y1),
  BIC(arma1_1)/length(data$y1),
  BIC(arma2_1)/length(data$y1),
  BIC(arma1_2)/length(data$y1),
  BIC(arma2_2)/length(data$y1)
)
out<-data.frame(matrix(aic, nrow=1))
out<-rbind(out, bic)
colnames(out)<-name
rownames(out)<-c('AIC', 'SIC')
###AIC ARMA(2,1), SIC AR(2)
out

       AR(2) ARMA(1,1) ARMA(2,1) ARMA(1,2) ARMA(2,2)
AIC 3.023947  3.034293  3.021437  3.029152  3.027627
SIC 3.073331  3.083677  3.083167  3.090882  3.101703
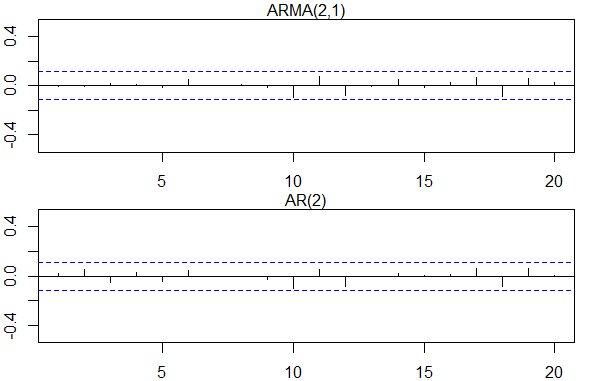
  • (4)

AICからはARMA(2,1)、SICからはAR(2)を選択した。

acf(arma2_1$residuals, xlim=c(1,20), ylim=c(-0.5,0.5))
acf(ar2$residuals, xlim=c(1,20), ylim=c(-0.5,0.5))

1_2.6.4.png

Box.test(arma2_1$residuals[1:20], type="Ljung")

    Box-Ljung test

data:  arma2_1$residuals[1:20]
X-squared = 0.013201, df = 1, p-value = 0.9085

Box.test(ar2$residuals[1:20], type="Ljung")

    Box-Ljung test

data:  ar2$residuals[1:20]
X-squared = 0.0979, df = 1, p-value = 0.7544
  • (5)

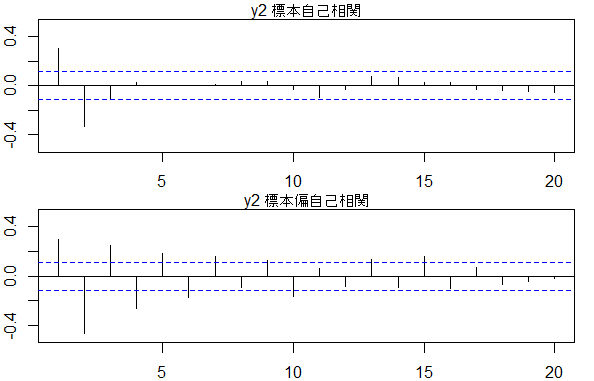
y2

acf(data$y2, xlim = c(1, 20), ylim = c(-0.5, 0.5))
mtext(text = 'y2 標本自己相関', side = 3)
pacf(data$y2, xlim = c(1, 20), ylim = c(-0.5, 0.5))
mtext(text = 'y2 標本偏自己相関', side = 3)

1_2.6.5.y2.png

####MA(3)
####ARMA(1,1),ARMA(2,1),ARMA(1,2),ARMA(2,2)
ma3<-Arima(data$y2, order=c(0, 0, 3))
arma1_1<-Arima(data$y2, order=c(1, 0, 1))
arma2_1<-Arima(data$y2, order=c(2, 0, 1))
arma1_2<-Arima(data$y2, order=c(1, 0, 2))
arma2_2<-Arima(data$y2, order=c(2, 0, 2))

name<-c('MA(3)', 'ARMA(1,1)', 'ARMA(2,1)', 'ARMA(1,2)', 'ARMA(2,2)')
aic<-c(
  AIC(ma3)/length(data$y2),
  AIC(arma1_1)/length(data$y2),
  AIC(arma2_1)/length(data$y2),
  AIC(arma1_2)/length(data$y2),
  AIC(arma2_2)/length(data$y2)
)
bic<-c(
  BIC(ma3)/length(data$y2),
  BIC(arma1_1)/length(data$y2),
  BIC(arma2_1)/length(data$y2),
  BIC(arma1_2)/length(data$y2),
  BIC(arma2_2)/length(data$y2)
)
out<-data.frame(matrix(aic, nrow=1))
out<-rbind(out, bic)
colnames(out)<-name
rownames(out)<-c('AIC', 'SIC')
###AIC MA(3), SIC MA(3)
out

       MA(3) ARMA(1,1) ARMA(2,1) ARMA(1,2) ARMA(2,2)
AIC 2.769046  2.859515  2.775498  2.818165  2.781784
SIC 2.830775  2.908899  2.837228  2.879895  2.855860

par(mfrow = c(1, 1))
acf(ma3$residuals, xlim=c(1,20), ylim=c(-0.5,0.5))

1_2.5.6.y2.2.png

Box.test(ma3$residuals[1:20], type="Ljung")

    Box-Ljung test

data:  ma3$residuals[1:20]
X-squared = 0.0066437, df = 1, p-value = 0.935

y3

###y3
par(mfrow=c(2,1))
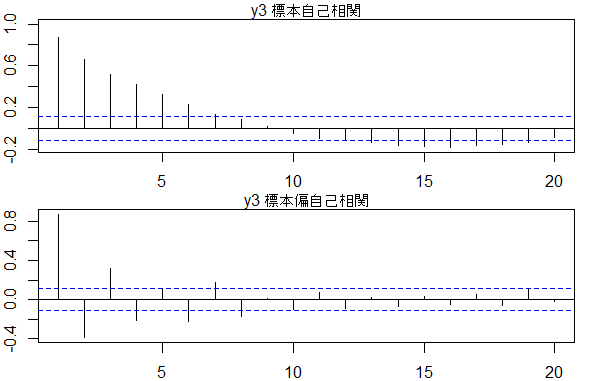
acf(data$y3, xlim=c(1, 20))
mtext(text = 'y3 標本自己相関', side = 3)
pacf(data$y3, xlim=c(1, 20))
mtext(text = 'y3 標本偏自己相関', side = 3)

1_2.6.5.y3.png

####AR(8), MA(7)
####ARMA(1,1),ARMA(2,1),ARMA(1,2),ARMA(2,2)
ar8<-Arima(data$y3, order=c(8, 0, 0))
ma7<-Arima(data$y3, order=c(0, 0, 7))
arma1_1<-Arima(data$y3, order=c(1, 0, 1))
arma2_1<-Arima(data$y3, order=c(2, 0, 1))
arma1_2<-Arima(data$y3, order=c(1, 0, 2))
arma2_2<-Arima(data$y3, order=c(2, 0, 2))

name<-c('AR(8)', 'MA(7)', 'ARMA(1,1)', 'ARMA(2,1)', 'ARMA(1,2)', 'ARMA(2,2)')
aic<-c(
  AIC(ar8)/length(data$y3),
  AIC(ma7)/length(data$y3),
  AIC(arma1_1)/length(data$y3),
  AIC(arma2_1)/length(data$y3),
  AIC(arma1_2)/length(data$y3),
  AIC(arma2_2)/length(data$y3)
)
bic<-c(
  BIC(ar8)/length(data$y3),
  BIC(ma7)/length(data$y3),
  BIC(arma1_1)/length(data$y3),
  BIC(arma2_1)/length(data$y3),
  BIC(arma1_2)/length(data$y3),
  BIC(arma2_2)/length(data$y3)
)
out<-data.frame(matrix(aic, nrow=1))
out<-rbind(out, bic)
colnames(out)<-name
rownames(out)<-c('AIC', 'SIC')
###AIC ARMA(1,2), SIC ARMA(1,1)
out

       AR(8)    MA(7) ARMA(1,1) ARMA(2,1) ARMA(1,2) ARMA(2,2)
AIC 3.115248 3.082550  3.069798   3.06590  3.065178  3.071635
SIC 3.238708 3.193663  3.119182   3.12763  3.126907  3.145711

par(mfrow = c(1, 1))
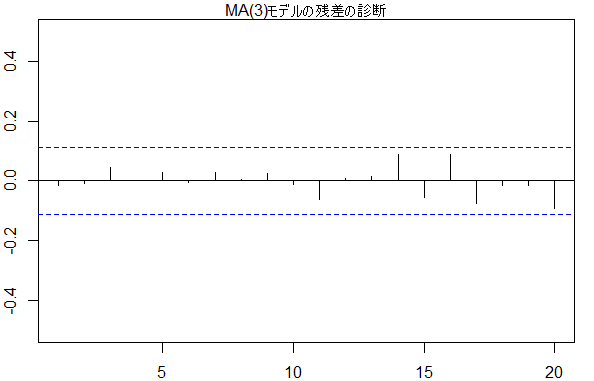
acf(arma1_2$residuals, xlim=c(1,20), ylim=c(-0.5,0.5))
mtext(text = 'ARMA(1,2)モデルの残差の診断', side = 3)

1_2.6.5.y3.2.png

Box.test(arma1_2$residuals[1:20], type="Ljung")

    Box-Ljung test

data:  arma1_2$residuals[1:20]
X-squared = 0.17219, df = 1, p-value = 0.6782

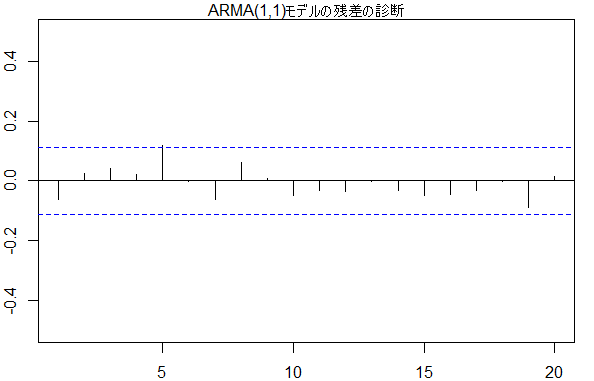
acf(arma1_1$residuals, xlim=c(1,20), ylim=c(-0.5,0.5))
mtext(text = 'ARMA(1,1)モデルの残差の診断', side = 3)

1_2.6.5.y3.3.png

Box.test(arma1_1$residuals[1:20], type="Ljung")

    Box-Ljung test

data:  arma1_1$residuals[1:20]
X-squared = 6.0017e-05, df = 1, p-value = 0.9938

⇒ 3章はプログラムを用いる章末問題がないので、次は 『経済・ファイナンスデータの計量時系列分析』章末問題をRで解く－第4章VARモデル－ へ

2
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
1