の演習問題を解いているが解答が本書内にもネット上にもない模様。自分の解答を晒して間違いにツッコミをいただき理解を深めようという試み。
第7章
- 問7.1
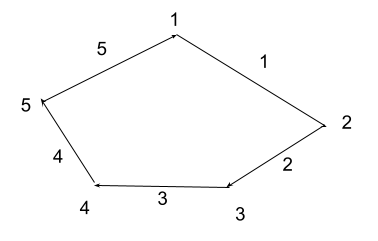
xの座標を(x_1, x_2)とする。 \\
xとP(x)を通る直線は傾きが\frac{1}{3}で\\
\begin{align}
y-x_2&=-\frac{1}{3}(x-x_1) \\
だから(0,0)と(1,3)を通る直線との交点は \\
\left\{
\begin{array}{l}
y&=3x\\
y-x_2&=-\frac{1}{3}(x-x_1) \\
\end{array}
\right.\\
より\\
x&=\frac{x_1+3x_2}{3}\\
y&=\frac{3}{10}(x_1+3x_2)\\
\\
線形関数となることを示せ、はわからず。\\
A&=
\begin{bmatrix}
\frac{1}{10} \frac{3}{10} \\
\frac{3}{10} \frac{9}{10} \\
\end{bmatrix}
\end{align}
- 問7.2
\begin{align}
y&=
\begin{bmatrix}
cos(-45^\circ) & -sin(-45^circ) & 0 \\
sin(-45^circ) & cos(-45^circ) & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\end{bmatrix}
から\\
A&=\begin{bmatrix}
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0 \\
-\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\end{align}
- 問7.3
\begin{align}
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & \cdots & \cdots & a_{2n} \\
\vdots & & & \vdots \\
a_{n-2,1} & \dots & \cdots & a_{n_2,n} \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n \\
\end{bmatrix}&=
\begin{bmatrix}
a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n \\
\vdots \\
\vdots \\
a_{n-2,1}x_1+a_{12}x_2+\cdots+a_{n-2,n}x_n \\
\end{bmatrix}
\begin{bmatrix}
x_2 \\
x_3 \\
\vdots \\
x_{n-1} \\
\end{bmatrix}\\
より\\
a_{11}, a_{13}, \cdots, a_{1n}&=0, a_{12}=1\\
a_{11}, a_{12}, a_{14}, \cdots, a_{1n}&=0, a_{13}=1\\
\vdots\\
a_{n-2,1}, \cdots, a_{n-2,n-2}, a_{n-2,n}&=0, a_{n-2,n-1}=1\\
\therefore A&=
\begin{array}{l}
\left.
\begin{bmatrix}
0 & 1 & 0 & 0 & \cdots & & & & 0 \\
0 & 0 & 1 & 0 & \cdots & & & & 0 \\
\vdots & & & & \ddots & & & & \vdots \\
0 & \cdots & & & \cdots & 0 & 1 & 0 & 0 \\
0 & \cdots & & & \cdots & 0 & 0 & 1 & 0 \\
\end{bmatrix}
\right\}n-2行
\end{array}\\
&\quad\quad\quad\quad\quad\quad\quad\quad n列
\end{align}
- 問7.4
- (a)
A=
\begin{bmatrix}
\frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0
& \frac{1}{2} & \frac{1}{2} \\
\end{bmatrix}
-
- (b)
A=
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 \\
\frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \\
0 & \frac{1}{2} & \frac{1}{2} & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\
0 & 0 & 0 & 0 & 1 \\
\end{bmatrix}
- 問7.5
\begin{align}
m&\le nのとき \\
uに対して&A^{\top}で要素を選択したのがv\\
m&\gt nのとき \\
uに対し&A^{\top}にて一部の要素は選択され、\\
一部の&要素の線形結合となるのがv
\end{align}
- 問7.6
接続行列の和を考える。\\
各有向辺は各ノードから出て必ずどこかのノードに入るから各行の和の総和は常に0となる。\\
各行をa_1, \cdots, a_nと置くと、\\
a_1 + \cdots + a_n=0 より、\\
a_1 = -(a_2 + \cdots + a_n)となり、\\
線形従属となる。\cdots\cdotsで良いかな?
- 問7.7
元のグラフの辺の方向を逆転させているから\\
接続行列の各要素の正負を逆転させれば良い\\
\therefore -A
- 問7.8
Ax+s=0 かつネットワーク内でフローの損失や増加はないからsの総和は0となる。\\
つまり、 \mathbf{1}^{\top}s=0
- 問7.9
- (a)
\begin{align}
D(v)&=\|A^{\top}v\|^2 \\
&=\sum_{辺(v,k)}(v_l-v_k)^2 \\
\end{align}\\
であり、辺の向きとは無関係なく2節点の差のみに依存するため。
\begin{bmatrix}
-1 & 0 & 0 & 0 & 1 \\
1 & -1 & 0 & 0 & 0 \\
0 & 1 & -1 & 0 & 0 \\
0 & 0 & 1 & -1 & 0 \\
0 & 0 & 0 & 1 & -1 \\
\end{bmatrix}
-
- (b)総和が0となる。 (で良いかな?)
-
- (c)?わかりません。
-
問7.11
\begin{bmatrix}
1 & -1 & 0 & 0 & 0 \\
0 & 1 & 0 & -1 & -1 \\
-1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & -1 & 0 & 0 \\
\end{bmatrix}
- 問7.12
- (a)
\mathbf{1} をm次元ベクトルとすると\\
\sum_{i+j=k+1}^{n+m-1}{\mathbf{1}_i\cdot a_j} \\
\begin{align}
k&=1: a_1 \\
k&=2: \mathbf{1}_1a_2+\mathbf{1}_2a_1=a_1+a_2 \\
k&=3: \mathbf{1}_1a_3+\mathbf{1}_2a_2+\mathbf{1}_3a_1=a_1+a_2+a_3 \\
\vdots \\
\end{align}\\
\therefore \sum_{i=1}^n{a_i}
-
- (b)
c_k=\sum_{i+j=l+1}^{n+q-1}{e_i\cdot a_j} \quad
e_i =
\left\{
\begin{array}{ll}
1 & i=k \\
0 & i\ne k
\end{array}
\right. \\
\therefore a_k
- 問7.13
ベクトルa, bが多項式p, qの係数を表すとすると、 \\
\mathbf{1}^{\top}a=p(1)、\mathbf{1}^{\top}b=q(1)だから \\
\begin{align}
右辺&:(\mathbf{1}^{\top}a)(\mathbf{1}^{\top}b)=p(1)q(1) \\
左辺&:\mathbf{1}^{\top}(ab)=p(1)q(1) \\
\end{align}\\
\therefore 左辺=右辺
- 問7.14
\begin{align}
h&=gr, g=(0.1, 0.4, 0.5, 0.2) \\
h_k&=\sum_{i+j=k+1}{g_i r_j}, k=1, \cdots, n+m-1 \\
h_1&=g_1r_1=0.1r_1 \\
h_2&=g_1r_2+g_2r_1=0.1r_2+0.4r_2 \\
h_3&=g_1r_3+g_2r_2+g_3r_1=0.1r_3+0.4r_2+0.5r_1 \\
H_4&=g_1r_4+g_2r_3+g_3r_2+g_gr_1=0.1r_4+0.4r_3+0.5r_2+0.2r_1 \\
\vdots \\
h_k&=g_1r_k+g_2r_{k-1}+g_3r_{k-2}+g_4r_{k-3}=0.1r_k+0.4r_{k-1}+0.5r_{k-2}+0.2r_{k-3} \\
\end{align} \\
となるから、\\
降雨の2日後の影響が最も強く、1日後の影響がその次で、4日後には降雨の影響がなくなる。
- 問7.15
- (a)
\begin{align}
z&=h*y\\
&=h(c*u) \\
&=(h*c)u \\
&\approx e_1*u
\end{align}
-
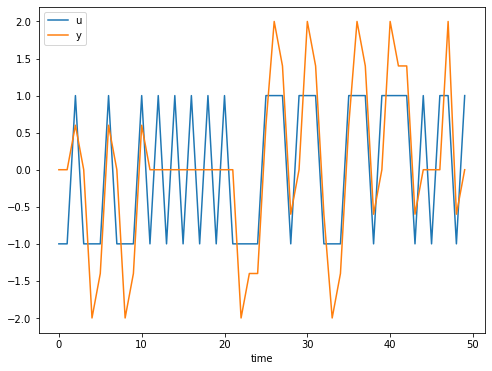
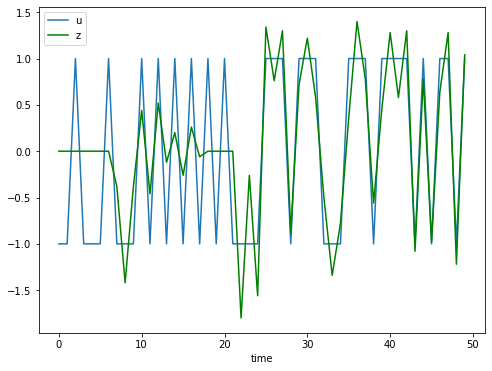
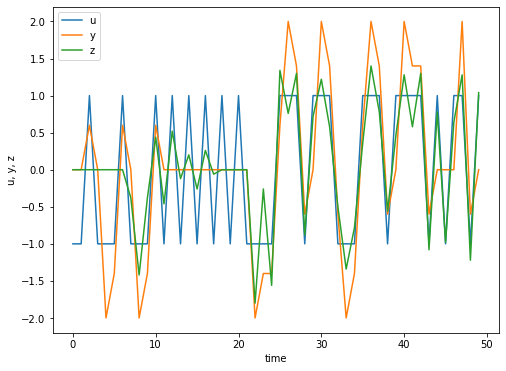
- (b)Pythonだとこんな感じ。yを受信するがzでuを概ね復元できている。
import matplotlib.pyplot as plt
import random
random.seed(12345)
c = [1.0, 0.7, -0.3]
h = [0.9, -0.5, 0.5, -0.4, 0.3, -0.3, 0.2, -0.1]
u = []
y = [0, 0]
z = [0, 0, 0, 0, 0, 0, 0]
for i in range(50):
u.append(1 if random.random() >= 0.5 else -1)
for i in range(2, 50):
y.append(c[0] * u[i] + c[1] * u[i-1] + c[2] * u[i - 2])
for i in range(7, 50):
z.append(h[0] * y[i] + h[1] * y[i-1] + h[2] * y[i - 2] + h[3] * y[i - 3] + h[4] * y[i - 4] + h[5] * y[i - 5] + h[6] * y[i - 6] + h[7] * y[i - 7])
plt.figure(figsize=(8,6))
plt.plot(list(range(50)), u, label = 'u')
plt.plot(list(range(50)), y, label = 'y')
plt.xlabel('time')
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
plt.plot(list(range(50)), u, label = 'u')
plt.plot(list(range(50)), z, label = 'z', c='green')
plt.xlabel('time')
plt.legend()
plt.show()
plt.figure(figsize=(8,6))
plt.plot(list(range(50)), u, label = 'u')
plt.plot(list(range(50)), y, label = 'y')
plt.plot(list(range(50)), z, label = 'z')
plt.xlabel('time')
plt.legend()
plt.show()