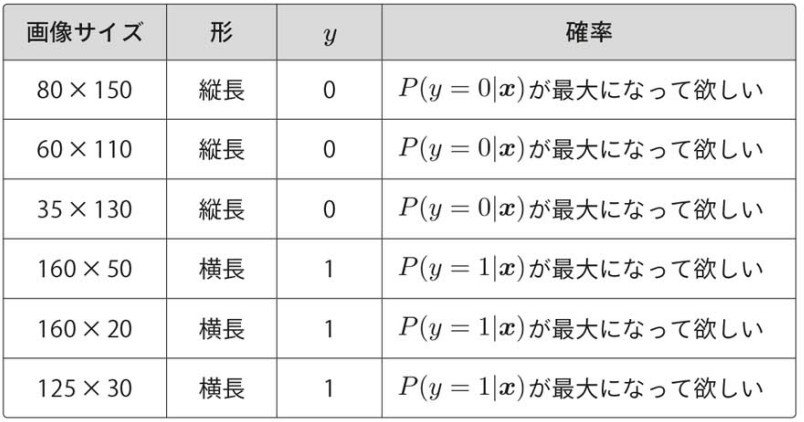
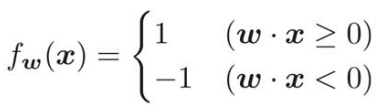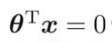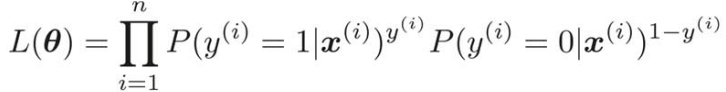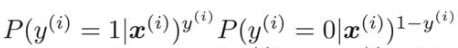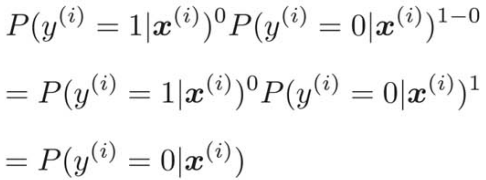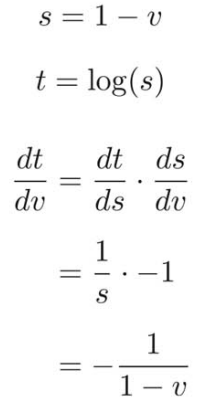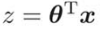復習と頭の整理のためにメモとして書いていきます。随時、追記していきます。
分類
画像が縦長か横長か、2つの分類先に分ける二値分類について考える。
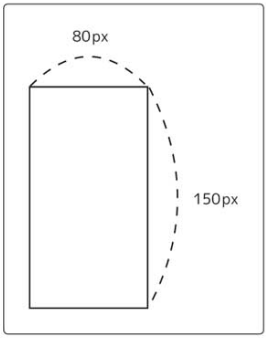

データ : 高さと横幅の部分
ラベル : 形の部分

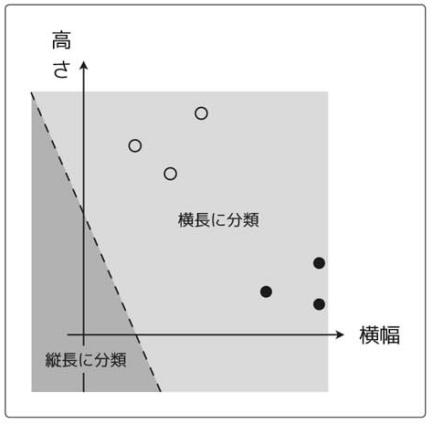
表の内容をプロットすると次のようになる。
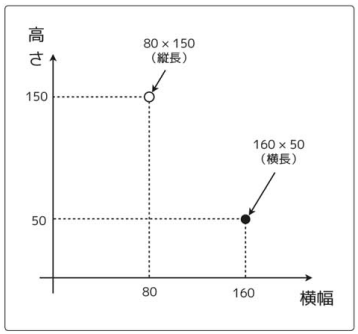
更に、データ数を増やしてみる。
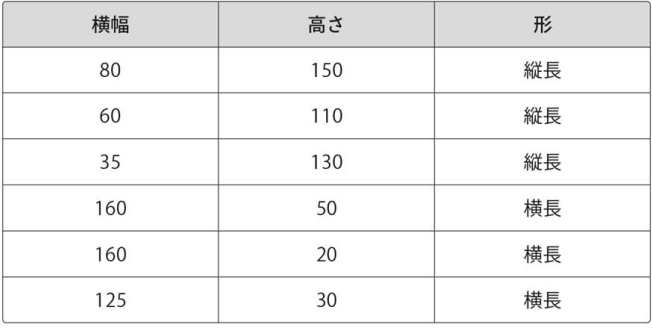
再度、プロットすると次のようになる。

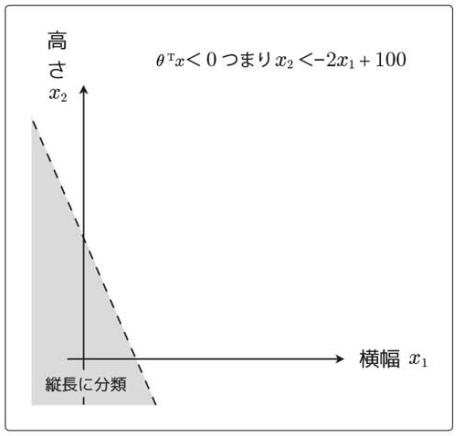
これは、次のように線を引いて分類できる。

分類の場合は、図形的に解釈するとわかりやすいから、大きさと向きを持った矢印のベクトルをイメージするといい。
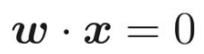
先の線は、重みベクトルを法線ベクトルとする直線ということになる。
(注意)
![]() は重みベクトルというパラメータで、法線は、ある直線に対して垂直なベクトルのこと。
は重みベクトルというパラメータで、法線は、ある直線に対して垂直なベクトルのこと。
ベクトル同士の内積について
実ベクトル空間の内積は各要素の積を足し上げたものだから、次の式と同じ意味ということ。
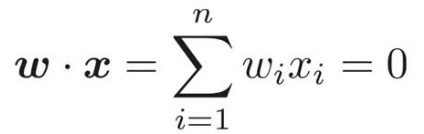
今回の縦幅と横幅を求める式は次のようになる。

![]() = (1, 1)のとき
= (1, 1)のとき

![]() となり、傾き-1の直線を表すということがわかる。
となり、傾き-1の直線を表すということがわかる。
(内積の式は直線のグラフを表す。)

重みベクトル![]() = (1, 1)を書き加えると、
= (1, 1)を書き加えると、![]() が直線に対して垂直になっていることがわかる。
が直線に対して垂直になっていることがわかる。
縦長か横長かを判定する関数(つまり1か-1を返す関数![]() )は識別関数という名前がついている。
)は識別関数という名前がついている。


 のとき、つまり重みベクトル
のとき、つまり重みベクトル の範囲内、つまり直線を挟んだ重みベクトルの反対側の範囲。
の範囲内、つまり直線を挟んだ重みベクトルの反対側の範囲。


重みベクトルの更新式は、次のようになる。
これをすべての学習データに対して繰り返し処理して重みベクトルを更新していく。
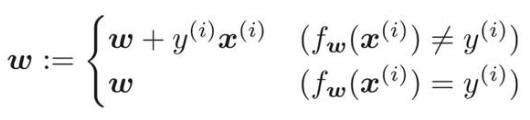
 は、識別関数による分類がうまくいかなかった場合。
は、識別関数による分類がうまくいかなかった場合。
(横幅と高さのベクトル![]() を識別関数に通して分るいした結果と、実際のラベルyが異なっている)
を識別関数に通して分るいした結果と、実際のラベルyが異なっている)
それに対して、 は、識別関数による分類がうまくいったということ。
は、識別関数による分類がうまくいったということ。
つまり、
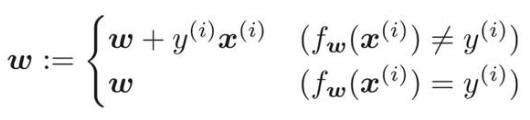
この式は、識別関数による分類に失敗した時だけ新しいパラメータに更新するよ、という式。
分類に成功した時は、そのまま![]() を代入しているので何も変わらない。
を代入しているので何も変わらない。
では、詳しく分類に失敗した時の更新式 を見ていく。
を見ていく。
重みベクトルは、回帰のパラメータ同様、ランダムな値で初期化するから、適当に以下のベクトルで考えてみる。

 というデータがあるとき、これでパラメータを更新することを考えてみる。
というデータがあるとき、これでパラメータを更新することを考えてみる。


お互いのベクトルはほぼ反対を向いているから![]() と
と![]() の成す角θは
の成す角θは になって、内積は負になる。
になって、内積は負になる。
したがって、識別関数![]() による分類は-1となる。
による分類は-1となる。
つまり、 になって、分類に失敗したという状態。
になって、分類に失敗したという状態。
更新式が適用され、![]() より、
より、
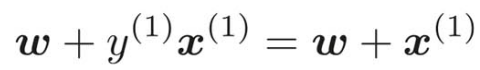
ここで面白いのは、新しい次の![]() は
は![]() で、その新しい重みベクトルに垂直な直線(識別関数)は回転したこと。
で、その新しい重みベクトルに垂直な直線(識別関数)は回転したこと。
 これで
これで![]() なので、内積が正になり、
なので、内積が正になり、![]() による分類は1になる。
による分類は1になる。
![]() なので、分類に成功したということになる。
なので、分類に成功したということになる。
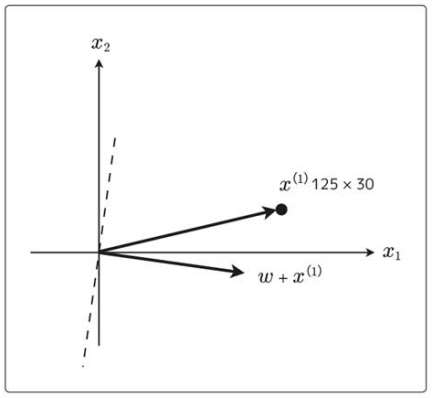
このように、パラメータの重みベクトルは更新されていく。
この更新をすべての学習データについて繰り返していくことがパーセプトロンの学習ということになる。
ロジスティック回帰/シグモイド関数
ロジスティック回帰は、分類を確率として考えるので、アプローチの仕方が異なる。
横長を1、縦長を0とすると、
Q. 縦長を今回−1にしなかったのは何故か?
更新式を簡潔にするための便宜上の理由。本当はどちらでもいい。
回帰の関数 は、勾配降下法を使ってθを学習し、そのθを使って未知のデータ
は、勾配降下法を使ってθを学習し、そのθを使って未知のデータ![]() に対する出力値を求めることができた。
に対する出力値を求めることができた。
このように、未知のデータがどのクラスに分類されるかを求める関数![]() が必要で、次のような式になる。
が必要で、次のような式になる。

ちなみに![]() =
= ![]() なので、
なので、 は、
は、![]() と書き換えることができる。
と書き換えることができる。
![]() を横軸、
を横軸、![]() を縦軸だとする、シグモイド関数は次のようなグラフになる。
を縦軸だとする、シグモイド関数は次のようなグラフになる。
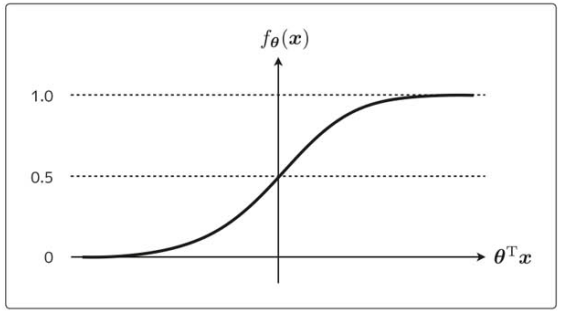
シグモイド関数は、 だから、分類を確率として考える上で便利。
だから、分類を確率として考える上で便利。
未知のデータ![]() が横長だとう確率
が横長だとう確率![]() は、次のように表すことができる。
は、次のように表すことができる。
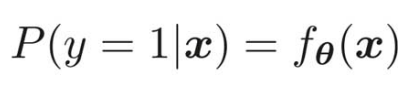
![]() の中の縦棒は、条件付き確率、つまり
の中の縦棒は、条件付き確率、つまり![]() というデータが与えられた時に横長(
というデータが与えられた時に横長(![]() )になる確率を表す。
)になる確率を表す。
 のとき、横幅である確率は70%だということ。=>横長に分類される。
のとき、横幅である確率は70%だということ。=>横長に分類される。
 は横幅の確率が20%ということ。=> 縦長に分類される。
は横幅の確率が20%ということ。=> 縦長に分類される。
つまり、![]() の結果を見て、0.5をしきい値として横長か縦長かを分類される。
の結果を見て、0.5をしきい値として横長か縦長かを分類される。


 は、
は、
 と書き直せる。
横軸を横幅(
と書き直せる。
横軸を横幅(


要するに、![]() を境界線として、分類している。
を境界線として、分類している。
このようにデータを分類するための直線のことを決定境界という。
今回は、パラメータθに適当な値を入れたので、上手く分類できていない。
次はそのθを求めるために、目的関数を定義して微分してパラメータの更新式を求める(ロジスティック回帰)。
![]() が横長である確率
が横長である確率 を
を![]() と定義したので、学習ラベル
と定義したので、学習ラベル![]() と
と![]() の関係は、
の関係は、
![]() のとき
のとき 、
、
![]() のとき、
のとき、
すべての学習データはお互い関係なく独立に発生すると考えると、この場合の全体の確率は、次のように表すことができる。

場合分けするより、1つの式にまとまって表記が簡単になっている。
目的関数がわかったところで、次は、目的関数を最大化するパラメータθを考える。
(回帰の時は誤差を最小化する、今考えているのは、同時確率。確率が高くなってほしいから、最大化する。)
対数尤度関数
これからは尤度関数を微分して、パラメータθを求めていく。
ただし、予め尤度関数は変形する(尤度関数の対数をとる)。
(確率は全て1以下の数で、同時確率のようなかけ算は、かけるほど値が小さくなっていくため。)

logは単調増加関数(グラフがずっと右上がりで、![]() なら
なら となるような関数
となるような関数![]() のこと。)で、そのグラフの形はこのような感じ。
のこと。)で、そのグラフの形はこのような感じ。

![]() なら
なら になっている。だから、尤度関数についても
になっている。だから、尤度関数についても なら
なら になる。
になる。
要するに、![]() を最大化することと
を最大化することと を最大化することは同じことになる。
を最大化することは同じことになる。
次に、尤度関数の微分について
ロジスティック回帰は、この対数尤度関数を目的関数として使うことになる。

これをパラメータθで微分していくと、

次のように置き換えて、

よって、
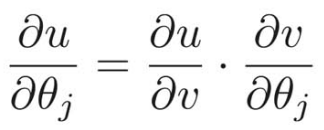
まずは、![]() から計算すると、
から計算すると、

次は、![]() を
を![]() で微分する。
で微分する。
ただし、 を微分することは、ややこしいので、以下のようなシグモイド関数の微分結果を利用して微分する。
を微分することは、ややこしいので、以下のようなシグモイド関数の微分結果を利用して微分する。


![]() を
を![]() で微分する部分が要するにシグモイド関数の微分のことなので、
で微分する部分が要するにシグモイド関数の微分のことなので、


結果をかけあわせて、


あとは、この式からパラメータ更新式を導き出すだけ。今は最大化することが目的なので、微分した結果の符号と同じ方向に動かさないといけない。

ηの前と、シグマの中の符号を入れ替えて、回帰の時と符号を合わせるようにして、次のようにも書ける。
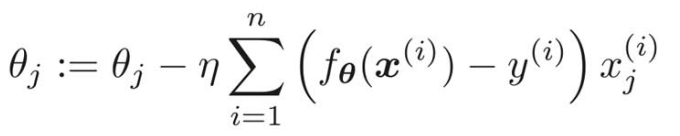
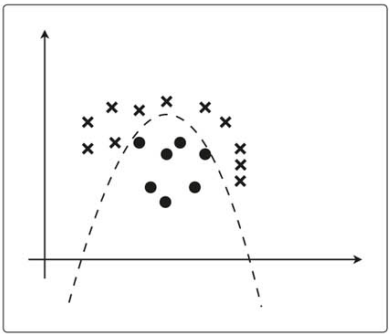
線形分離不可能
ロジスティック回帰を線形分離不可能な問題に適用する。
線形分離不可能な問題も、曲線であれば分類はできる。つまり次数を増やす必要がある。
![]() のとき、
のとき、
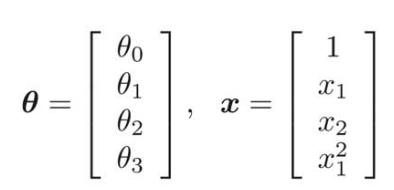
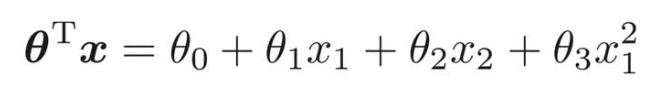
θが以下のようなベクトルだったときのグラフの形を考えると、
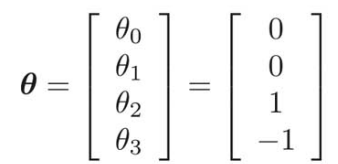
θをとりあえず代入して、

よって、![]() となる。
となる。
グラフに書くと次のようになる。

このようにして、線形分離不可能な問題を解いて行く。
(今回はパラメータθがまだ適切ではないので、データを正しく分類できていない。)
例えば、好きなように次数を増やして、複雑な形の決定境界にすることもできる。