Go to Qiita Advent Calendar 2024 Top
LoginSignup
172
176

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

JuliaAdvent Calendar 2016

Day 3
@antimon2(Shunsuke GOTOH)in有限会社来栖川電算

Julia のススメ 〜 Deep Learning のための Julia 〜

Last updated at Posted at 2016-12-02
1 / 58

TL;DR

  • Julia は速いよ。
  • Julia は行列演算簡単だよ。
  • Julia は Deep Learning 向きだよ。
  • Julia はそもそも書きやすいよはかどるよ！
  • Julia 良いよ Julia！

初めに

自己紹介

自己紹介

  • 名前：後藤 俊介
  • 所属：有限会社 来栖川電算
  • 言語：Python, Julia, Ruby, Scala（勉強中）, …
  • twitter: @antimon2
  • Facebook: antimon2
  • GitHub: antimon2
  • Qiita: @antimon2

Julia

Julia とは

Julia で Deep Learning

  • 既存のライブラリ（外部パッケージ）：
  • 行列（テンソル）計算が簡単だから、自分でも手軽に実装出来ます！
    • この記事（スライド）では実装例を紹介！

Julia インタープリタ3

と、基本的な演算4。

julia> VERSION
v"0.5.0"

julia> 1 + 2
3

julia> 7 / 5  # 除算
1.4

julia> 7 ÷ 5  # 整数除算
1

julia> 3 ^ 2  # べき乗
9

ベクトル

Julia では1次元配列がベクトル。

julia> a = [1, 2, 3, 4, 5]
5-element Array{Int64,1}:
 1
 2
 3
 4
 5

julia> a[1]   # Julia は 1-origin
1

julia> println(a[2:3])  # 範囲指定は両端含む
[2,3]

ベクトルの演算5 

julia> x = [1., 2., 3.];

julia> y = [3., 1., 2.];

julia> x + y  # `x .+ y` と書いても同じ（elementwise operation）
[4., 3., 5.]

julia> x .* y # これは `x * y` と書くとNG
[3., 2., 6.]

julia> x ⋅ y  # 内積（dot積、`dot(x, y)` と書いても同じ）
11.0

julia> x × y  # 外積（cross積、`cross(x, y)` と書いても同じ）
[1., 7., -5.]

行列

Julia では2次元配列が行列6。

julia> A = [1 2; 3 4]   # この記法は MATLAB/Octave 由来
2×2 Array{Int64,2}:
 1  2
 3  4

julia> A'   # `○'` は転置行列の記法（これも MATLAB/Octave 由来）
2×2 Array{Int64,2}:
 1  3
 2  4

行列の演算7 

julia> A = [1 2; 3 4]; B = [3 0; 0 6];

julia> A + B  # A .+ B でも同様
2×2 Array{Int64,2}:
 4   2
 3  10

julia> A .* B   # elementwise multiply
2×2 Array{Int64,2}:
 3   0
 0  24

julia> A * B   # matrix multiply
2×2 Array{Int64,2}:
 3  12
 9  24

行列とベクトルの演算

ベクトル（1次元配列）は縦ベクトルの扱い。

julia> A = [1 2; 3 4]; x = [1, 2];

julia> A * x  # 2x2行列と2次元ベクトルの積→2次元ベクトル
[5,11]

julia> A .+ x   # broadcast
2×2 Array{Int64,2}:
 2  3
 5  6

julia> A .+ x'  # broadcast2（ベクトルの転置は1xN行列（行ベクトル））
2×2 Array{Int64,2}:
 2  4
 4  6

Julia で
ニューラルネット

シグモイド関数

の紹介を兼ねた関数定義89例。

function sigmoid(x)
    1.0 ./ (1.0 .+ exp(-x))
end

※↑xがスカラーでもベクトルでも（行列でも）そのまま動作する。

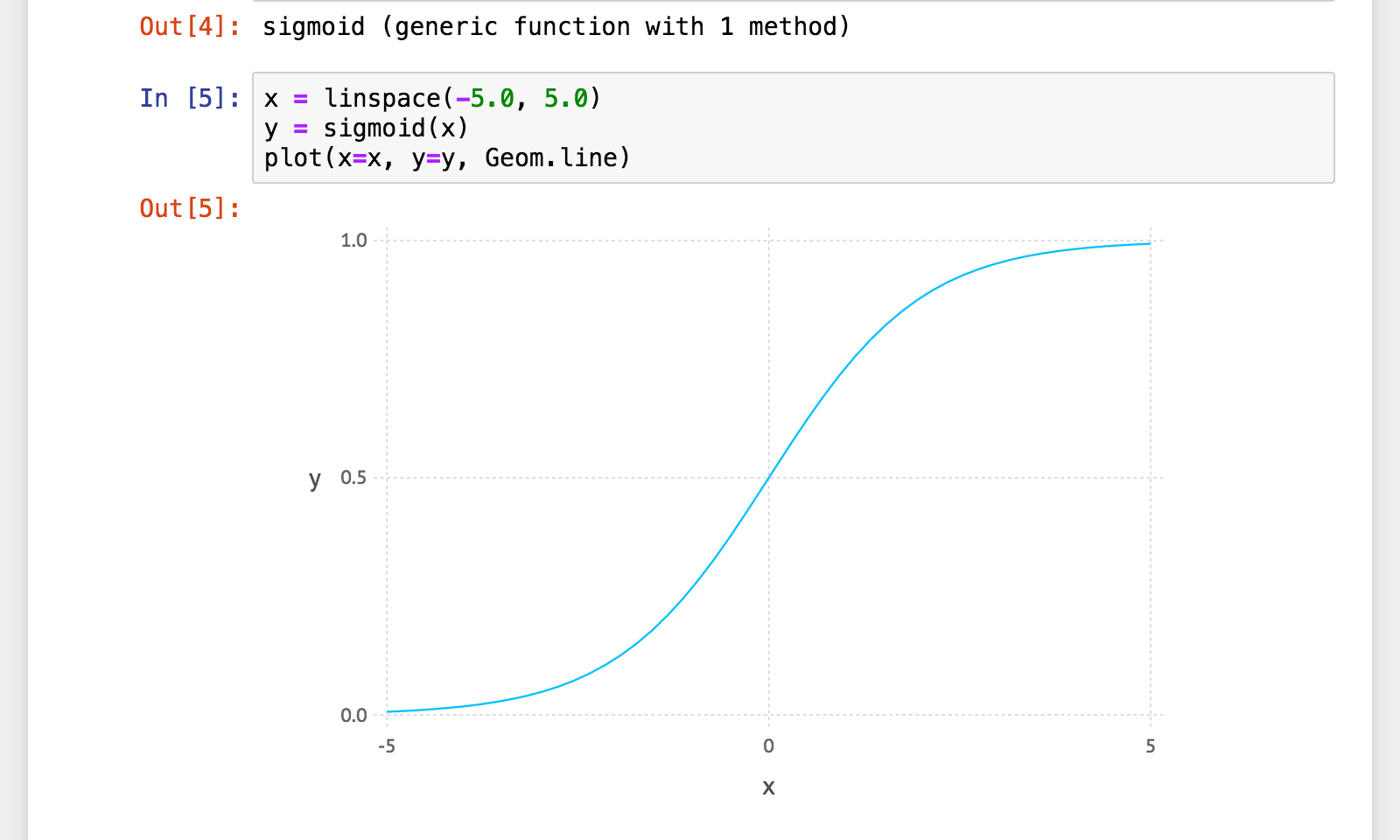
Gadfly10 を使ってプロット

# Pkg.add("Gadfly")
using Gadfly

x = linspace(-5.0, 5.0)
y = sigmoid(x)
plot(x=x, y=y, Geom.line)

Chapter3_sigmoidplot_800x480.png

3層ニューラルネット

function nn3lp(x)
    W1 = [0.1 0.2; 0.3 0.4; 0.5 0.6];
    b1 = [0.1, 0.2, 0.3];
    W2 = [0.1 0.2 0.3; 0.4 0.5 0.6];
    b2 = [0.1, 0.2];
    W3 = [0.1 0.2; 0.3 0.4];
    b3 = [0.1, 0.2];

    a1 = W1 * x .+ b1
    z1 = sigmoid(a1)
    a2 = W2 * z1 .+ b2
    z2 = sigmoid(a2)
    a3 = W3 * z2 .+ b3
    identity(a3)
end

julia> x = [1.0, 0.5];

julia> y = nn3lp(x)
2-element Array{Float64,1}:
 0.316827
 0.696279

簡単ですね！

ソフトマックス関数

の紹介を兼ねた少し複雑な関数定義111213例。

function softmax{T}(a::AbstractVector{T})
    c = maximum(a)  # オーバーフロー対策
    exp_a = exp(a .- c)
    exp_a ./ sum(exp_a)
end

function softmax{T}(a::AbstractMatrix{T})
    # 行列の場合：各列ベクトルに`softmax`を適用
    mapslices(softmax, a, 1)
end

julia> a = [0.3, 2.9, 4.0];

julia> softmax(a)
[0.0182113, 0.245192, 0.736597]

julia> A = [0.3 1001.0; 2.9 1000.0; 4.0 999.0];

julia> softmax(A)
3×2 Array{Float64,2}:
 0.0182113  0.665241
 0.245192   0.244728
 0.736597   0.0900306

MNIST

手書き数字のサンプルデータセット（MNIST）。
追加パッケージ14で簡単に利用可能。

julia> # Pkg.add("MNIST")

julia> using MNIST

julia> x_train, t_train = traindata();

julia> x_test, t_test = testdata();

julia>size(x_train)
(784,60000)

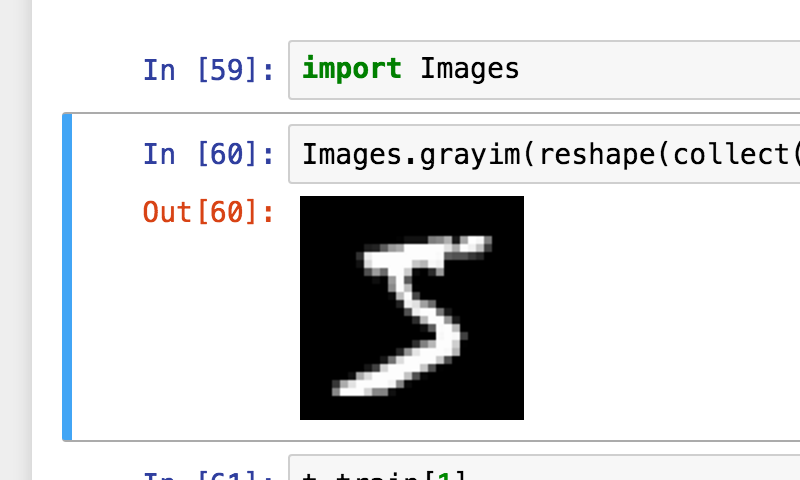
画像確認

画像の表示には、追加パッケージ Images.jl15 を利用。

julia> # Pkg.add("Images")

julia> using Images

julia> grayim(reshape(collect(UInt8, x_train[:, 1]), 28,28)')

Chapter3_grayim_400x240.png

訓練済モデル読込

追加パッケージ JLD16 で変数の読込（および書込）が可能1718。

julia> # Pkg.add("JLD")

julia> using JLD

julia> network = load("/path/to/sample_network.jld")
Dict{String,Any} with 6 entries:
  "W2" => Float32[-0.10694 0.299116 … 0.100016 -0.0222066; 0.0159125 -0.0332223…
  "W3" => Float32[-0.421736 -0.524321 … -0.544508 1.07228; 0.689445 -0.143625 ……
  "b3" => Float32[-0.0602398,0.00932628,-0.0135995,0.0216713,0.0107372,0.066197…
  "W1" => Float32[-2.90686f-5 -1.88106f-5 … -0.000386883 1.09472f-6; -3.09976f-…
  "b2" => Float32[-0.0147111,-0.0721513,-0.00155692,0.121997,0.116033,-0.007549…
  "b1" => Float32[-0.0675032,0.0695926,-0.0273047,0.0225609,-0.220015,-0.220388…

MNIST の予測

function predict(network, x)
    W1 = network["W1"]
    b1 = network["b1"]
    W2 = network["W2"]
    b2 = network["b2"]
    W3 = network["W3"]
    b3 = network["b3"]

    a1 = W1 * x .+ b1
    z1 = sigmoid(a1)
    a2 = W2 * z1 .+ b2
    z2 = sigmoid(a2)
    a3 = W3 * z2 .+ b3
    softmax(a3)
end

julia> predict(network, x_train[:, 1])
10-element Array{Float64,1}:
 0.0106677  
 0.000158301
 0.000430344
 0.215528   
 5.69069e-6 
 0.7676     
 3.01649e-5 
 0.00311578 
 0.00166548 
 0.000798537

julia> indmax(predict(network, x_train[:, 1])) - 1
5

julia> t_train[1]
5.0   # 合ってますね！

汎化精度（テストデータの正解率）

julia> y = predict(network, x_test)
10×10000 Array{Float64,2}:
 8.44125e-5   0.00483633  1.03583e-7   …  0.000624385  0.000428828
 2.63506e-6   0.00110459  0.988973        0.000767557  2.0043e-6  
 0.000715494  0.944252    0.00428949      0.000124992  0.00254057 
 0.00125863   0.0143091   0.00178321      0.000642085  2.01689e-6 
 1.1728e-6    5.69896e-7  0.000131734     0.00126703   0.000559177
 4.49908e-5   0.00667604  0.000759407  …  0.907499     0.00031262 
 1.62693e-8   0.0275334   0.00046891      0.00274028   0.996148   
 0.997065     1.27084e-6  0.00226997      3.81287e-5   4.34994e-7 
 9.37447e-6   0.00128642  0.00123787      0.0862065    6.37568e-6 
 0.000818312  4.78647e-8  8.67147e-5      8.9935e-5    3.77514e-7

julia> p = reshape(mapslices(indmax, y, 1), (length(t_test),)) .- 1;

julia> mean(p .== t_test)
0.9352  # 93.52%！

簡単ですね！

ニューラルネットの学習

One-hot Vector

ラベルが離散値の場合に、その値を One-hot Vector に変換。19

function onehot{T}(::Type{T}, t::AbstractVector, l::AbstractVector)
    r = zeros(T, length(l), length(t))
    for i = 1:length(t)
        r[findfirst(l, t[i]), i] = 1
    end
    r
end
@inline onehot(t, l) = onehot(Int, t, l)

julia> t_train[1:3]
[5.0, 0.0, 4.0]

julia> onehot(Float32, t_train[1:3], 0:9)
10×3 Array{Float32,2}:
 0.0  1.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  1.0
 1.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0

交差エントロピー誤差20 

function crossentropyerror(y::Vector, t::Vector)
    δ = 1e-7  # アンダーフロー対策
    # -sum(t .* log(y .+ δ))
    -(t ⋅ log(y .+ δ))
end
function crossentropyerror(y::Matrix, t::Matrix)
    batch_size = size(y, 2)
    δ = 1e-7
    # -sum(t .* log(y .+ δ)) / batch_size
    -vecdot(t, log(y .+ δ)) / batch_size
end
  • t は One-hot Vector（またはそれを並べた行列）（以下同様）

誤差逆伝播法

を意識した各層の設計21。

abstract AbstractLayer

全結合層（Affine Layer）2223 

type AffineLayer{T} <: AbstractLayer
    W::AbstractMatrix{T}
    b::AbstractVector{T}
    x::AbstractArray{T}
    dW::AbstractMatrix{T}
    db::AbstractVector{T}
    function (::Type{AffineLayer}){T}(W::AbstractMatrix{T}, b::AbstractVector{T})
        lyr = new{T}()
        lyr.W = W
        lyr.b = b
        lyr
    end
end

順伝播・逆伝播の定義 24 

function forward{T}(lyr::AffineLayer{T}, x::AbstractArray{T})
    lyr.x = x
    lyr.W * x .+ lyr.b
end

function backward{T}(lyr::AffineLayer{T}, dout::AbstractArray{T})
    dx = lyr.W' * dout
    lyr.dW = dout * lyr.x'
    lyr.db = _sumvec(dout)
    dx
end
@inline _sumvec{T}(dout::AbstractVector{T}) = dout
@inline _sumvec{T}(dout::AbstractMatrix{T}) = vec(mapslices(sum, dout, 2))
@inline _sumvec{T,N}(dout::AbstractArray{T,N}) = vec(mapslices(sum, dout, 2:N))

ReLU層

type ReluLayer <: AbstractLayer
    mask::AbstractArray{Bool}
    ReluLayer() = new()
end

function forward{T}(lyr::ReluLayer, x::AbstractArray{T})
    mask = lyr.mask = (x .<= 0)
    out = copy(x)
    out[mask] = zero(T)
    out
end

function backward{T}(lyr::ReluLayer, dout::AbstractArray{T})
    dout[lyr.mask] = zero(T)
    dout
end

SoftmaxWithLossLayer

type SoftmaxWithLossLayer{T} <: AbstractLayer
    loss::T
    y::AbstractArray{T}
    t::AbstractArray{T}
    (::Type{SoftmaxWithLossLayer{T}}){T}() = new{T}()
end

順伝播・逆伝播の定義

function forward{T}(lyr::SoftmaxWithLossLayer{T}, x::AbstractArray{T}, t::AbstractArray{T})
    lyr.t = t
    y = lyr.y = softmax(x)
    lyr.loss = crossentropyerror(y, t)
end

function backward{T}(lyr::SoftmaxWithLossLayer{T}, dout::T=1)
    dout .* _swlvec(lyr.y, lyr.t)
end
@inline _swlvec{T}(y::AbstractArray{T}, t::AbstractVector{T}) = y .- t
@inline _swlvec{T}(y::AbstractArray{T}, t::AbstractMatrix{T}) = (y .- t) / size(t)[2]

2層ニューラルネット（2LP）

簡単のため2層で例示。25

type TwoLayerNet{T}
    a1lyr::AffineLayer{T}
    relu1lyr::ReluLayer
    a2lyr::AffineLayer{T}
    softmaxlyr::SoftmaxWithLossLayer{T}
end

2LP 外部コンストラクタ26 

function (::Type{TwoLayerNet{T}}){T}(input_size::Int, hidden_size::Int, output_size::Int,
        weight_init_std::Float64=0.01)
    W1 = weight_init_std .* randn(T, hidden_size, input_size)
    b1 = zeros(T, hidden_size)
    W2 = weight_init_std .* randn(T, output_size, hidden_size)
    b2 = zeros(T, output_size)
    a1lyr = AffineLayer(W1, b1)
    relu1lyr = ReluLayer()
    a2lyr = AffineLayer(W2, b2)
    softmaxlyr = SoftmaxWithLossLayer{T}()
    TwoLayerNet(a1lyr, relu1lyr, a2lyr, softmaxlyr)
end

推測27 

function predict{T}(net::TwoLayerNet{T}, x::AbstractArray{T})
    a1 = forward(net.a1lyr, x)
    z1 = forward(net.relu1lyr, a1)
    a2 = forward(net.a2lyr, z1)
    # softmax(a2)
    a2
end

損失関数（目的関数）

function loss{T}(net::TwoLayerNet{T}, x::AbstractArray{T}, t::AbstractArray{T})
    y = predict(net, x)
    forward(net.softmaxlyr, y, t)
end

正解率

function accuracy{T}(net::TwoLayerNet{T}, x::AbstractArray{T}, t::AbstractArray{T})
    y = vec(mapslices(indmax, predict(net, x), 1))
    mean(y .== t)
end

勾配計算（誤差逆伝播法）2829 

immutable TwoLayerNetGrads{T}
    W1::AbstractMatrix{T}
    b1::AbstractVector{T}
    W2::AbstractMatrix{T}
    b2::AbstractVector{T}
end

function Base.gradient{T}(net::TwoLayerNet{T}, x::AbstractArray{T}, t::AbstractArray{T})
    # forward
    loss(net, x, t)
    # backward
    dout = one(T)
    dz2 = backward(net.softmaxlyr, dout)
    da2 = backward(net.a2lyr, dz2)
    dz1 = backward(net.relu1lyr, da2)
    da1 = backward(net.a1lyr, dz1)
    TwoLayerNetGrads(net.a1lyr.dW, net.a1lyr.db, net.a2lyr.dW, net.a2lyr.db)
end

勾配適用30 

function applygradient!{T}(net::TwoLayerNet{T}, grads::TwoLayerNetGrads{T}, learning_rate::T)
    net.a1lyr.W -= learning_rate .* grads.W1
    net.a1lyr.b -= learning_rate .* grads.b1
    net.a2lyr.W -= learning_rate .* grads.W2
    net.a2lyr.b -= learning_rate .* grads.b2
end

学習（SGD）

# using MNIST

_x_train, _t_train = traindata();
_x_test, _t_test = testdata();
x_train = collect(Float32, _x_train) ./ 255   # 型変換+正規化
t_train = onehot(Float32, _t_train, 0:9)      # One-hot Vector 化
x_test = collect(Float32, _x_test) ./ 255     # 型変換+正規化
t_test = onehot(Float32, _t_test, 0:9)        # One-hot Vector 化

iters_num = 10000;
train_size = size(x_train, 2); # => 60000
batch_size = 100;
learning_rate = Float32(0.1);

train_loss_list = Float32[];
train_acc_list = Float32[];
test_acc_list = Float32[];

iter_per_epoch = max(train_size ÷ batch_size, 1)  # => 600

network = TwoLayerNet{Float32}(784, 50, 10);

for i = 1:iters_num
    batch_mask = rand(1:train_size, batch_size)
    x_batch = x_train[:, batch_mask]
    t_batch = t_train[:, batch_mask]
    
    # 誤差逆伝播法によって勾配を求める
    grads = gradient(network, x_batch, t_batch)
    
    # 更新
    applygradient!(network, grads, learning_rate)
    
    _loss = loss(network, x_batch, t_batch)
    push!(train_loss_list, _loss)

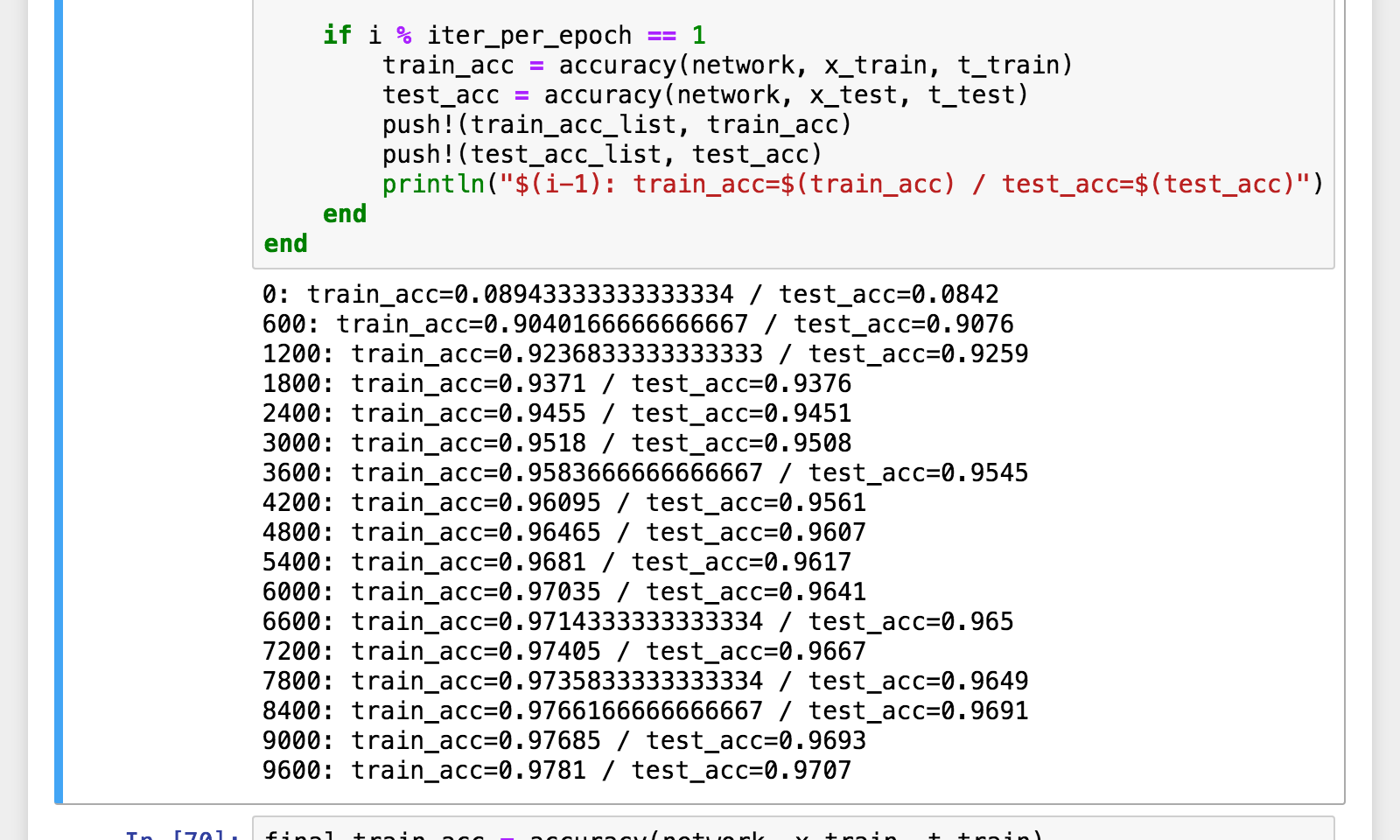
    if i % iter_per_epoch == 1
        train_acc = accuracy(network, x_train, t_train)
        test_acc = accuracy(network, x_test, t_test)
        push!(train_acc_list, train_acc)
        push!(test_acc_list, test_acc)
        println("$(i-1): train_acc=$(train_acc) / test_acc=$(test_acc)")
    end
end

Chapter5_leaning_800x480.png

精度（正解率）確認

final_train_acc = accuracy(network, x_train, t_train)
final_test_acc = accuracy(network, x_test, t_test)
push!(train_acc_list, final_train_acc)
push!(test_acc_list, final_test_acc)
println("final: train_acc=$(final_train_acc) / test_acc=$(final_test_acc)")
# => final: train_acc=0.97685 / test_acc=0.9686

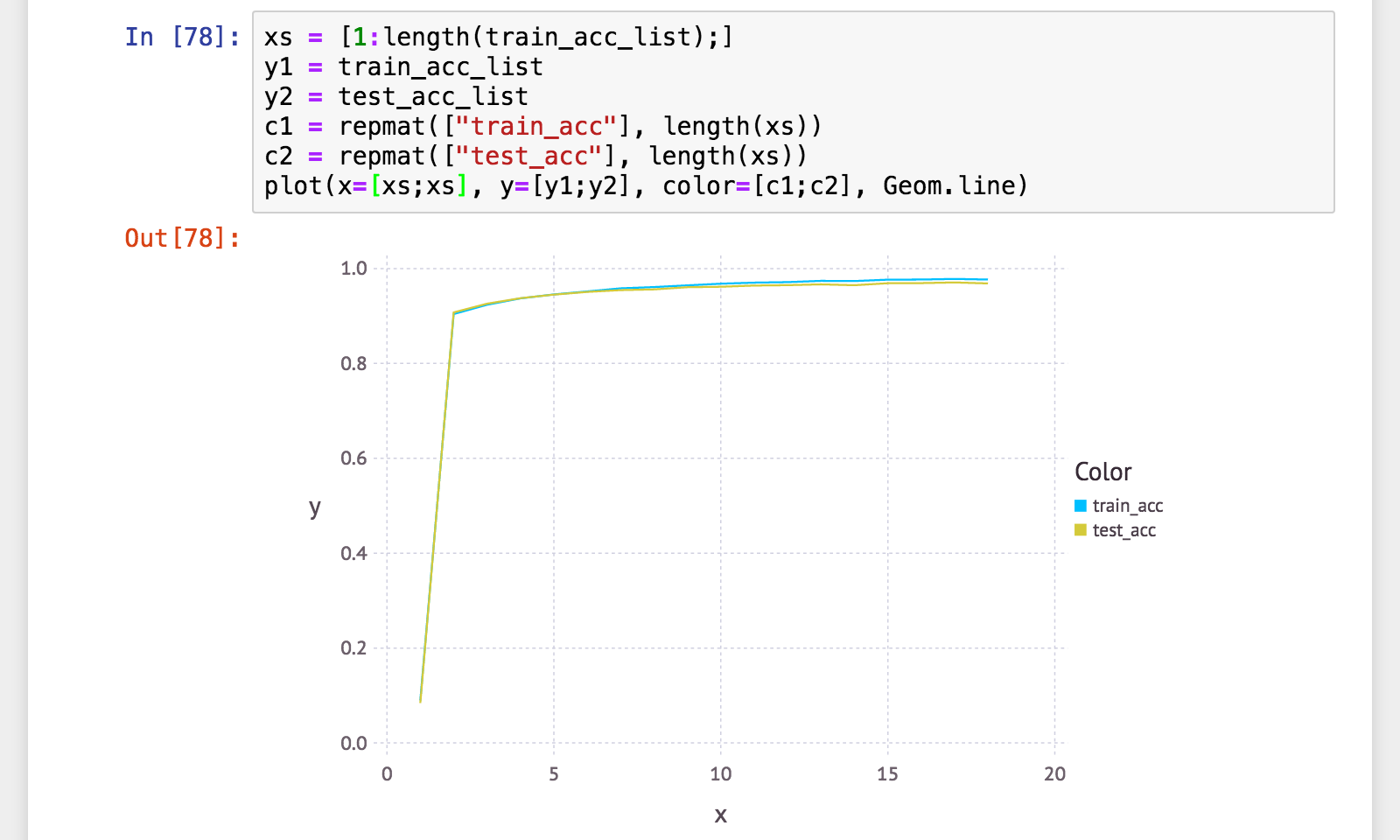
Chapter5_accuracyplot_800x480.png

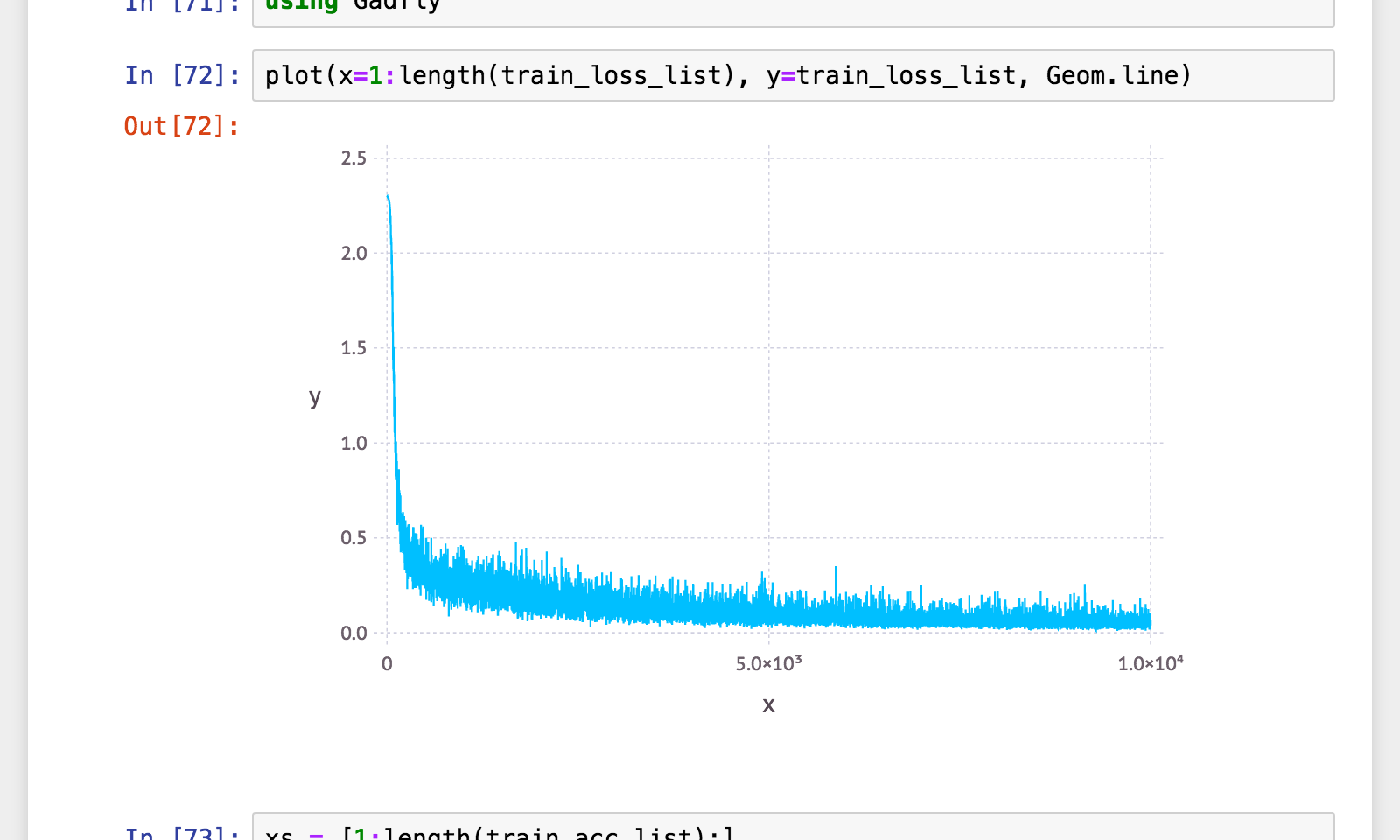
学習曲線

Chapter5_trainlossplot_800x480.png

簡単ですねっ！

発展

  • 最適化手法（SGD の代わりに）
    • Momentum
    • AdaGrad
    • Adam
  • Batch Normalization
  • 正則化
    • Weight Decay
    • Dropout
  • CNN

参考

  1. 古い記事の転記ミス（コピペミス）を修正しただけで「この記事は最終更新日から1年以上が経過しています。」が消えてしまうので注意書きを追加。 ↩

  2. この記事は、約1年前の最新版である Julia v0.5.x をベースにしています。2018/01/06 現在の最新 v0.6.x、近い将来の正式版である v1.x では一部 Warning が出るか、期待通りに動作しない可能性もあるので、十分ご注意ください。 ↩

  3. この記事では Julia v0.5.0 以降を対象とします。v0.4.x 以前では一部動作しない可能性があります。 ↩

  4. /は、整数に適用すると浮動小数になる（Python3と同様の動作）。整数除算は（//ではなく）÷。またべき乗は（**ではなく）^。 ↩

  5. ここに出てくる ⋅ は、（日本語の中黒「・」ではなく）U+22C5 'DOT OPERATOR'。Julia コンソールや、Julia 用プラグインのインストールされたエディタなら、\cdot と入力してTabキーを押すと変換できます。また×は日本でも掛け算記号としておなじみ（たいていのIMEで「かける」で変換可能）ですがこれも \times+Tab で入力できます。 ↩

  6. NumPy の行列の書式（np.array([[1, 2], [3, 4]])）より圧倒的に記述量少ない！ ↩

  7. * が通常の行列積！ NumPyの A.dot(B) と比べて記述量も少ないし直観的！ ↩

  8. ワンラインで sigmoid(x) = 1.0 ./ (1.0 .+ exp(-x)) と定義することも可能。 ↩

  9. Ruby などと同様で、最後に実行した文（式）の値が戻り値（return 省略可能）。明示的に return ～ を書くことも可能。 ↩

  10. http://gadflyjl.org/ 。Julia 定番のプロットライブラリ。 ↩

  11. 関数引数についている ::Xxx は型アノテーション。関数呼び出し時に型が合わなければエラーになる（動的型チェック）。 ↩

  12. 関数名と引数リストの間の {T} は、型パラメータアノテーション。引数の型 AbstractVectorとかAbstractMatrix が型パラメータを受け取るがそれが未定の時の表記。ここに {T<:AbstractFloat} と書くことで「T は AbstractFloat の sub type」という指定（型境界の指定）も可能。 ↩

  13. 同じ関数名で異なる引数（型および個数）の関数を多重定義できる。実行時（関数呼び出し時）に適切な引数を持つ関数が実行される（多重ディスパッチと言います）。またこの仕組みのおかげでif文が減らせる！ ↩

  14. http://github.com/johnmyleswhite/MNIST.jl ↩

  15. http://github.com/timholy/Images.jl ↩

  16. http://github.com/JuliaIO/JLD.jl ↩

  17. ここでロードしているサンプルデータは、ゼロから作る Deep Learning のサンプルデータ sample_weight.pkl を読み込んで変形した上で .jld 形式で保存したものです。 ↩

  18. Dict は Julia の辞書型。Dict{String,Any} は、「キーが文字列（String）、値は何でもあり（Any）の辞書」という意味。 ↩

  19. 第1引数の ::T という書式は、最初の引数が T 型のインスタンスであることを意味する（その値は問わない（不使用））。また ::Type{T} だと、そこには 型そのもの（IntとかFloat64とか） が来ることを表す。 ↩

  20. コメントアウトしてある -sum(t .* log(y .+ δ)) は定義をそのまま書き下したもの。⋅ または vecdot() はそれを書き直したもので、（ベクトル（1次元配列）にした上で）内積を取った方が省メモリかつ高速！ ↩

  21. キーワード abstract で始まるのは抽象型。メンバーを持つことはできない（型の階層構造（ツリー構造）構築のためのもの） ↩

  22. キーワード type は、型（具象型）の定義。 type A <: B という書式は「B という型を継承した A という型を定義」という意味になる。{T} は型パラメータの指定。 ↩

  23. type ～ end 内に記述した、型名と同名の関数は、内部コンストラクタとなる。主に「宣言したメンバのうちの一部のみを受け取ってインスタンスを生成」する際に利用する。new() は内部コンストラクタ内のみで利用できる特別な関数（メモリ確保）。 ↩ ↩2

  24. @inline は、「今から書く関数定義を（可能ならば）インライン展開してね」という指定。なお @～ は Julia のマクロ呼び出しの書式（インライン指定はマクロとして実装されている）（Java の Annotation でもないし Python の Decorator とも別物）。 ↩

  25. 今までの type 定義では中に内部コンストラクタ23（＝型名と同名の関数）を指定してきた。ここではその記述がないがこの場合、デフォルトコンストラクタが暗黙に定義される。引数はメンバを宣言順にすべて（この場合 TwoLayerNet{T}(a1lyr::AffineLayer{T},relu1lyr::ReluLayer,a2lyr::AffineLayer{T},softmaxlyr::SoftmaxWithLossLayer{T})）。 ↩

  26. type ～ end の定義外で定義した、型名と同名の関数は、外部コンストラクタ（として利用できる関数）となる。引数に対して複雑な処理をしてから、内部コンストラクタ（デフォルトコンストラクタ含む）に引き渡してインスタンスを生成する（という用途が一般的）。 ↩

  27. ここでは softmax() かけない。 ↩

  28. immutable キーワードで始まる型定義は「不変型」の定義。type で定義した型と比較して、メンバーの変更を許可しない。 ↩

  29. Julia 標準の gradient という関数が既に存在するので、関数多重定義時に Base.gradient とするか、事前に import Base.gradient を実行しておかないと怒られる。 ↩

  30. Julia では、引数の内容（メンバー等）を変更する関数名に ! をつける慣習がある（おそらくRuby由来）。 ↩

172
176
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
172
176

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?