はじめに
電子署名に関する記事の中で、軽く触れておこうと思ったところ、結構長くなりそうなので、単独の記事として起こしました。
電子署名と言えば、古典的にはRSA署名、DSA、近年使われているのはECDSAやEdDSA(ed25519)といった方式がありますが、その具体的な内容は割愛します。
世の中、電子署名の説明は色々ありますので、そちらをご参照…と言いたかった所なのですが、残念なことに不適切な説明というのも多いのです。
現実へのアナロジー
電子署名とは、現実世界の署名( 日本でならまだ印鑑の方がメジャーでしょうか ) をデジタルデータ上に実現したものと見ることができます。
つまり、あるデータに関して当事者が署名を施すことで、そのデータの内容に関する承認の意志を示すもの、逆に署名を受け取った人からすれば、署名者が後から「いやそんなの知らない」と否認する ( しらばっくれる ) ことを防止するための証拠となるものです。
これは、現実の署名であれば本人でなければ有効な署名はできない( 例えば、偽者の筆跡やコピーによるものは鑑定によりバレる ) ということに基づくものです。
電子署名でも本人でなければ施せないという点は同様ですが、ただデジタルデータであるがため大きく異なる点が1つあります。それは、一旦出回ったデータは幾らでもコピーすることができるというデジタルデータの特性によるものです。
どういうことかというと、署名データに対して、それが原本だから○、コピーだから×なんて判断をすることには意味がないため、電子署名ではすべからく対象のデータ毎に署名の内容が異なる( 現実的には、同一の署名データができる可能性を極力低くする ) 必要があります。
逆にデータ毎に異なる署名ということは、署名単体の真贋ではなくて、その対象データと署名の内容が整合しているかどうかを見るということでもあります。整合していない場合は、署名の作られ方が不適切だったり、或いは、署名データか対象のデータが改ざんされたと判断できます。
つまり、電子署名はデータの改ざん検出の機能も備えるということです。
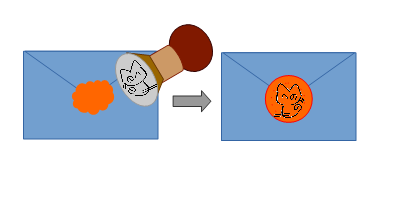
そういう意味では、現実世界の署名や印鑑というよりは、手紙の封をするときに用いる**封緘 ( シーリングスタンプ )**の方が近いとも言えます。手紙を封筒に入れて封蝋 ( シーリングワックス ) で封じると共に、そこに独自の印章を刻むものですね。
その封が壊れてない限りは ( 他の人に同じ封はできませんから )、内容に他者の手が入ってないということの保証となるわけです。尤も現実の封緘の場合は「他者の目に触れていないことが分かる」という面も大きいとは思うのですが。電子署名の場合は内容の隠匿の目的はありませんから。
署名に関する3つの処理
ということで、電子署名は現実世界での署名、印鑑、封緘の機能を実現するものなのですが、そうすると次の2種類の処理が必要です。
- 署名(署名作成)/sign
対象のデータから、署名者独自の署名データを作成すること。 - 検証(署名検証)/verify
対象のデータと署名との整合性を確認すること。成功した場合は「確かにその本人による署名である」と、失敗した場合は「不適切な署名、或いは、データの改ざんがあった」と判断できる。
ここで、署名が本人以外にできてしまっては問題ですし、逆に検証は誰にでもできてくれないと困ります。2種類の処理に非対称性があるわけです。
そのため、もう1種類、この非対称性に関わる処理を挙げる必要があるでしょう。
- 鍵生成(鍵ペア生成)
署名を行うために必要な、その人独自の署名鍵と、検証を行うために必要な、一般に公開する、署名鍵と対になる検証鍵のペアを作り出す。
公開・非公開という観点から、署名鍵のことを秘密鍵、検証鍵のことを公開鍵とも言います。一般的にはそちらの方が恐らく通りが良いと思いますが、機能面がぼやけるきらいがあります。
いわば、人毎に独自な印鑑や印章が署名鍵に相当し、検証鍵に相当するのは…、そうですね、専属の鑑定人と言ったところでしょうか。
もっと言うと、一般に広く出回って貰うわけですから、ネオ・サイタマにいそうなバイオクローン・カンテイニンが妥当かと思います。
非対称性の実現
さて、上で挙げた処理の非対称性ですが、どうやればそんなことが実現できるでしょうか。
この点については、実際に使われている署名方式であるDSA/ECDSAについて説明した記事がありますから、そちらを見て貰っても良いのですが。
その記事とも重複する話にはなりますが、例えば高校までの数学で習うべき乗の指数法則、これが非対称性を作る1つの例になります。
指数の法則としては次の2つです。
x^n\times x^m=x^{n+m} \\
(x^n)^m=x^{n\times m}
これを踏まえて次の計算を考えてみます。
- 署名対象のデータとして $m=5$ があるとする。
- A は事前に署名鍵 $x=4$ を保持し、検証鍵 $\chi=2^4=16$ を公開している。
- A は次のようなデータを作成し、それを署名としてBに送る
- 適当な秘密の数として $k=3$ を選び、$\rho=2^3=8$ を計算する。
- $m,\rho$ から、両者の合計13を計算し、円周率 $\pi=3.14159,26535,89793,23846\cdots$ の小数点以下13桁目をとって$h=7$とする。
- $\sigma=2^{k+x\times h}=2^{3+4\times 7}=2^{31}=2147483648$ を計算する。
- 計算した値のペア $(\rho,\sigma)=(8,,2147483648)$ を送る
- B は、署名対象のデータ$m=5$と、検証鍵$\chi=16$、送られてきた署名 $(\rho,\sigma)=(8,,2147483648)$ から次の計算で確認を行う。
- A と同様に$m,\rho$から$h=7$を計算する。
- $\sigma'=\rho\times \chi^h=8\times 16^7=2147483648$を計算する。
- $\sigma=\sigma'$であることから、署名は正当と判断する。
Aのみが持つ$x=4,k=3$と、Bがアクセスできる情報である$\chi=16,\rho=8$、異なる数値を使った処理であるにも関わらず、同じ$\sigma=\sigma'$が導き出せたということで、非対称性が実現できているわけです。
また、$h$の決定に$m$が関わりますから$m$が変われば署名データも変化します。( この例では10パターンしか扱えませんから、衝突の頻度が酷いことになりますが )
このカラクリは、次のような指数法則の活用です。
\begin{eqnarray}
\sigma'&=&\rho\times \chi^h \\
&=&2^k\times (2^x)^h \\
&=&2^k\times 2^{x\times h} \\
&=&2^{k+x\times h} = \sigma
\end{eqnarray}
もちろんこの例では、$\chi=16\rightarrow x=4$ や $\rho=8\rightarrow k=3$ というのは実際にはべき乗の逆演算である対数として簡単に導出できてしまいます。が、同じような計算構造を持ちかつ逆演算が困難な数の世界があれば…。実用化されている電子署名は、そのような数的構造を利用している方式だったりするわけです。
※この例は離散対数問題という、DSA等で広く使われている構造を取り上げた形になっているわけですが、もちろん他の数的構造による電子署名も有り得ます。
良くある勘違い
さて、電子署名に関して取り上げざるを得ないのは、おそらくまだ情報が整理されてない頃に出回ってしまった勘違い、デマについてです。
ここまでの機能面について、流石に大きく外した説明はないと思うのですが。その技術面の説明で必ずと言っていい程出てくるのは、
- ここに公開鍵暗号があるじゃろ?
- 普通は公開鍵で暗号化、秘密鍵で復号するじゃろ?
- でもハッシュデータを秘密鍵で暗号化すれば、それが公開鍵で復号できるんじゃ!!
- 復号して得られたデータがハッシュデータと一致したとすれば、それは対応した秘密鍵で暗号化された証じゃな?
- つまりこれが電子署名の仕組みじゃ!
というようなものです。( 日本語のサイトに関わらず英語のサイトでも同様のようです )
これは幾つかの問題があります。
まず1つ目。そもそもの問題として、上で挙げた簡単なサンプルですら、この説明に合ってないというところ。
確かに有名な公開鍵暗号であるRSA暗号、電子署名であるRSA署名の2者はこの説明に近い関係があるのですが、一部の方式にしか適用できない話を以て全体を語ろうとする、いわば木を見て森を見ずな説明になっているわけです。
伝説の麻雀打ちであるアカギであれば「背の立つところまでしか海に入っていないのに、俺は海を知ったと公言しているようなもの」と指摘するところでしょうか。
次に2つ目。これは小さな点ではありますが、そのRSAに対してすら適切とは言えないところです。正確には、
- RSA暗号における秘密鍵による復号とRSA署名における秘密鍵による署名
- RSA暗号における公開鍵による暗号化とRSA署名における公開鍵による検証
この組み合わせが、ほぼ同じ計算を行っているということです。つまり良くある説明では、逆の処理を混同していることになりますね。
※ 暗号化と復号は同一視できないのか? というと、そのような実装も可能ではあるのですが、現実にはそうなっていません。
最後に3つ目。これが最も厄介な点なのですが、署名を説明するために(狭義の)暗号の用語を使うことで、概念そのものをぼかして混同させてしまうことです。
署名に求められるものは本人しかできないという独自性であって、秘匿を目的とした暗号化とは異なるものですし、検証はあくまで整合性を確認するものであって、何かを復元したいわけではありません。
一時的に分かったつもりになれるかも知れませんが、その延長上に正解も応用もありません。いわばまやかしです。
この話をすると「細かい話はいろいろあるのかも知れないが、簡易な説明としては良いんではないか」と反論が来ることもあるのですが、深掘りしていないがために粗がある話と、一見分かり易そうなだけで根本的に合ってない話は区別すべきかと思います。
※というより、後者は普通にデマと呼ぶものでしょう。
まとめ
では、最後に電子署名についてまとめです。
- 電子署名とは、現実の署名や印鑑、封緘に相当するものである。
- 電子署名は、署名者の承認の意志を示す、或いは否認を防止する証となるものである。
- 電子署名は、署名対象データの改ざん検出の機能も持つ。
- 電子署名には、署名、検証、鍵生成の3種類の処理がある
- 署名には本人のみが保持する署名鍵を、検証には一般に公開された検証鍵を使うという非対称性がある。
- 「ハッシュデータを秘密鍵で暗号化」という広く出回っている説明はデマである。