0. はじめに

背景：ついにKaggleに登録したので、とりあえずやってみました。（遅い）
主旨：データを準備して、分析して、モデリングして、予測して、結果評価の一連の流れを紹介する（この記事はモデリングまで→つづき）。数学的な細かいところとか、妥当性とか厳密なところは一旦スルーします（そのうちロジスティック回帰の解説は書きます）。
環境：Kaggle Kernel Notebook

1. データ分析の準備

タイタニックの生存者データを入手する
- Kaggleを始めたらとりあえずやる例のコンペからデータを入手します。
Kaggle KernalでNotebookを作成する
- Competitionページの"New Notebook"をクリックします。
データを読み込む
- コンペのページからNotebookを作成すると，1つ目のボックスがこんな感じになっているはずなので，そのまま実行します。
- csvデータを読み込んで，dataframeとして格納する

train_csv = pd.read_csv('../input/titanic/train.csv', sep=',')
train_csv.head()

データの概要を調べる

# データの次元
train_csv.shape

# 出力結果
(891, 12)

891人の乗客のデータが入っているようです。


# 各行の欠損値数
train_csv.isnull().sum()

# 出力結果
PassengerId      0
Survived         0
Pclass           0
Name             0
Sex              0
Age            177
SibSp            0
Parch            0
Ticket           0
Fare             0
Cabin          687
Embarked         2
dtype: int64

AgeとCabinの欠損値が多いですね。

2. データを分析して説明変数を選ぶ

データの内容は，コンペのページに詳しく書いてあるので割愛します。
今回のデータでは，タイタニック号の乗客の属性から誰が生存できるかを予測します。
その乗客の属性がいくつかあるのですが，どの属性をどのように使っていくかをデータ分析をしながら決めていきます。

2.0. 目的変数を確認する

乗客が生存できたかどうかは、Survivedに0/1で格納されています。
0であれば死亡、1であれば生存です。
どのくらいの人が生き残ったのでしょうか。

# 生存確率
train_csv['Survived'].mean()

# 出力結果
 0.3838383838383838

4割弱の人が生き残ったようです。

train_csv['Survived'].value_counts()

# 出力結果
0    549
1    342
Name: Survived, dtype: int64

人数にしてみるとこんな感じです。

それでは，各属性と生存(Survived)の関係を見ていきます。

2.1. Pclass (チケットクラス)

1-3までの整数値が入っています。
数字が小さい方がいいクラスのようです。
映画を見ていると上位クラスの乗客が優先的に救命ボートに乗っていたように思います。
Survivedとのクロス集計をして、影響を見てみます*1。

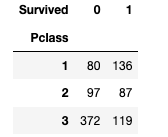
pd.crosstab(train_csv['Pclass'], train_csv['Survived'])

3rdクラスの乗客の死亡率が他のクラスと比べて圧倒的に高いですね。
逆に、1stクラスの乗客は生存率が高いです。
やはり良いクラスであればあるほど生存率が高いので、今回はこのままモデルに使います。

2.2. Name

何かしら関係があるかもしれませんが、因果を説明しにくいので今回は使いません。
(敬称だけ抜き出せば何かあるかもしれない。)

2.3. Sex（性別）

maleとfemaleがそのまま文字列で入っていますね。
非常時の際は女性の生存が優先され傾向にあるので、この場合も男性より女性の方が生存している人が多そうです。
Survivedとクロス集計します。

pd.crosstab(train_csv['Sex'], train_csv['Survived'])

女性は生存者が多いですが、男性は生存者が少ないです。
なので、女性ダミーを作ってモデルに入れます。

2.4. Age（年齢）

年齢は数値で入っていますが、多少欠損値があります。
分析の段階では、欠損値を除いて比べます。
一般的に考えれば、若い方の方が生存しやすいかと考えられます。
そのため、死亡した乗客と生存した乗客の平均年齢を比べてみます。*2

# 死亡者の平均年齢
train_csv[(train_csv['Age'].isnull() == False) & (train_csv['Survived'] == 0)].Age.mean()

# 出力結果
30.62617924528302

# 生存者の平均年齢
train_csv[(train_csv['Age'].isnull() == False) & (train_csv['Survived'] == 1)].Age.mean()

# 出力結果
28.343689655172415

生存者の方が若いですね。
ただし、このままでは欠損値があるのでモデルに入れられません。
一番手っ取り早くてよく取られている方法が、そのデータの代表値(平均や中央値)で補完することです。
今回は、欠損値は全体の平均値で補完してモデルに入れていきます。

2.5. SibSpとParch

SibSpは兄弟や配偶者、Parchは親や子供の人数が入っています。
家族が多い方が探してもらいやすそうなので、生存してそうな感じはします。
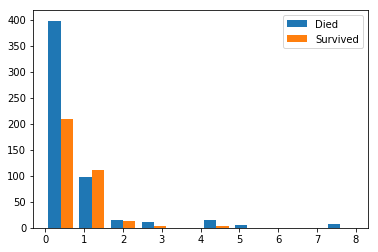
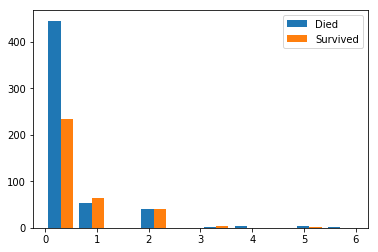
生存者と死亡者それぞれのSibSp/Parchのヒストグラムを描いてみます。

import matplotlib.pyplot as plt

# SibSp
plt.hist([train_csv[train_csv['Survived']==0].SibSp, train_csv[train_csv['Survived']==1].SibSp], label=['Died', 'Survived'])
plt.legend()

#Parch
plt.hist([train_csv[train_csv['Survived']==0].Parch, train_csv[train_csv['Survived']==1].Parch], label=['Died', 'Survived'])
plt.legend()

どちらも0人の人は死亡者が多いですが、1人でもいる人は生存者が多いか変わらないくらいです。
おひとりさまに辛い現実。
SibSpもParchも分布は似ているので、今回は代表的にParchを使います。
(似たような変数を入れると多重共線性を引き起こすため)
Parchは0人の人と1人以上の人でダミー変数化してモデルに入れます。

2.6. Ticket

何かしら関係は出るかもしれませんが、番号と英字の意味がよくわからないので影響があったとしても説明できません。
なので、今回は使いません。

2.7. Fare（運賃）

金額が整数値で入っています。
高い人ほど生き残っていそうですね。

# 死亡者
train_csv[train_csv['Survived']==0].Fare.mean()

# 出力結果
22.117886885245877

# 生存者
train_csv[train_csv['Survived']==1].Fare.mean()

# 出力結果
48.39540760233917

だいぶ差が出ましたね。
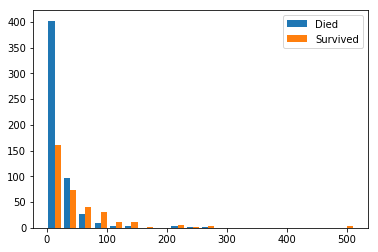
分布も見てみましょう。

plt.hist([train_csv[train_csv['Survived']==0].Fare, train_csv[train_csv['Survived']==1].Fare], label=['Died', 'Survived'], bins=20)
plt.legend()

少し見にくいですが、運賃が高いと生存者の方が多いみたいです。
なので、そのままモデルに入れます。

2.8. Cabin

欠損値が多すぎるので今回は利用を見送りました。

2.9. Embarked（乗船地）

どこから乗ったか3つの拠点で表されています。
乗船地による居住地特有の健康・経済状態、人種、乗船時間の違いが生存率に影響を与えるかもしれません。
欠損値がありますが、微々たるものなので一旦無視します。

pd.crosstab(train_csv['Embarked'], train_csv['Survived'])

S(Southampton)から乗客した人の死亡者数が多いですね。
Sダミーを作ってモデルに入れましょう。

なぜ、Southamptonの乗客の死亡者が多いのでしょうかね。
誰か知ってたら教えてください。

3. ロジスティック回帰でモデリングする

分析した結果を踏まえてモデリングしていきましょう。

3.1. データの加工

モデリング自体は簡単ですが、変数を加工する必要があります。
こんな感じ。

train = pd.DataFrame()
train = train.drop(['Name', 'SibSp', 'Ticket', 'Cabin'] , axis=1) # 使わない列を落とす

# 女性ダミーを作る
train['Female'] = train['Sex'].map(lambda x: 0 if x == 'male' else 1 ).astype(int)

# 年齢の欠損値を平均値で補完する
train['Age'].fillna(train['Age'].mean(), inplace=True)

# Parchが0人とそれ以上のダミーを作る
# Parch=0のとき0、Prach>=1のとき1
train['Parch_d'] = train['Parch'].map(lambda x: 0 if x == 0 else 1).astype(int)

# EmbarkedがSとそれ以外のダミーを作る
train['Embarked_S'] = train['Embarked'].map(lambda x: 0 if x == 'S' else 1).astype(int)

3.2. モデリング

そして、モデリングします。

# モデルの生成
from sklearn.linear_model import LogisticRegression
X = train[['Pclass', 'Age', 'Parch_d', 'Fare', 'Female', 'Embarked_S']]
y = train['Survived']

model = LogisticRegression()
result = model.fit(X, y)

3.3. モデリングの結果

まず、モデルがどんなモデルになったのか確認します。

# 係数
result.coef_
# 出力結果
rray([[-1.02255162e+00, -2.89166539e-02, -7.14935760e-02,
         1.19056911e-03,  2.49662371e+00, -4.29002495e-01]]

# 切片
result.intercept_
# 出力結果
array([1.98119965])

Female（女性ダミー）が最も影響を与えていそうです。

次に、作成したモデルが良いものなのかを見てみましょう*3。
まずは、決定係数を出してみます。

model.score(X, y)

# 出力結果
0.792368125701459

意外と悪くなさそうです。
決定係数はR²とも言われますが、先ほど作ったモデルの予測値がどの程度実際のデータに当てはまっているかを表します。（上記の値は、訓練データでの値）
0~1で表され、1に近いほどよく予測できているモデルというわけです。

今度は、テストデータで予測して確認してみましょう。
予測編に続きます。
→
https://qiita.com/anWest/items/cad88fe7b6f26fe86480

4. 備考

*1：厳密にやるのであれば、カイ二乗検定の必要がある
*2：本来なら、t検定と効果量を算出するべき
*3：モデルを評価する指標は色々あり、目的によって使い分ける必要がある

Kaggleのハローワールド、タイタニック号の生存者をロジスティック回帰で予測してみるーモデリング編ー