LoginSignup
9
5

More than 5 years have passed since last update.

@amb_00

Pythonで二分探索木を使った探索アルゴリズムをつくった！

Last updated at Posted at 2018-07-02

使ったもの

Python 3.6.0

二分探索木とは？

動的集合を取り扱うための多くの操作が利用できるデータ構造

今回扱う二分探索木
image.png

実装

search.py
# 節点(key,parent,left,rightをメンバ変数に持つ)
class Node:
    def __init__(self, key, parent=None, left=None, right=None):
        self.key = key
        self.p = parent
        self.left = left
        self.right = right

    def __repr__(self):
        return 'Node(%s)' % repr(self.key)

    # 探索
    def search(self, k):
        if self is None or k == self.key:
            return self
        if k < self.key:
            return self.left.search(k)
        else:
            return self.right.search(k)

    # 最小値
    def minimum(self):
        while self.left:
            self = self.left
        return self

    # 最大値
    def maximum(self):
        while self.right:
            self = self.right
        return self

    # 次節点
    def successor(self):
        if self.right:
            return self.right.minimum()
        y = self.p
        while y and self == y.right:
            self = y
            y = y.p
        return y

    # 前節点
    def predecessor(self):
        if self.left:
            return self.left.maximum()
        y = self.p
        while y and self == y.left:
            self = y
            y = y.p
        return y

    # 二分探索木のルートを返すメソッド
    def root(self):
        while self.p:
            self = self.p
        return self

    # 挿入
    def insert(self, value):
        z = Node(value)
        y = None
        self = self.root()
        while self:
            y = self
            if z.key < self.key:
                self = self.left
            else:
                self = self.right
        z.p = y
        if y is None:
            pass
        elif z.key < y.key:
            y.left = z
        else:
            y.right = z

    # 節点(自分)を削除して、子の節点に差し替えるメソッド(deleteメソッドの一部)
    def transparent(self, v):  # selfは削除される節点、vは差し替える節点
        if self.p is None:
            pass
        elif self == self.p.left:  # 節点が親の左部分木に属する場合
            self.p.left = v
        else:  # 節点が親の右部分木に属する場合
            self.p.right = v
        if v:
            v.p = self.p

    # 削除
    def delete(self):
        if self.left is None:  # 右の子のみを持つ場合
            y = self.right
            self.transparent(y)
        elif self.right is None:  # 左の子のみを持つ場合
            y = self.left
            self.transparent(y)
        else:  # 子を二つ持つ場合
            y = self.right.minimum()
            if y.p != self:
                y.transparent(y.right)
                y.right = self.right
                y.right.p = y
            self.transparent(y)
            y.left = self.left
            y.left.p = y
        return y.root()  # 新しく構成した二分木を返す


def main():
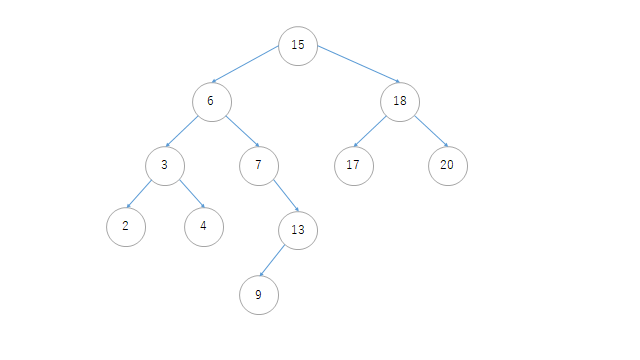
    # データセット
    r = Node(15)
    x1 = Node(6, r)
    x2 = Node(18, r)
    x3 = Node(3, x1)
    x4 = Node(7, x1)
    x5 = Node(17, x2)
    x6 = Node(20, x2)
    x7 = Node(2, x3)
    x8 = Node(4, x3)
    x9 = Node(13, x4)
    x10 = Node(9, x9)

    # 後からleft,rightを代入
    r.left, r.right = x1, x2
    x1.left, x1.right = x3, x4
    x2.left, x2.right = x5, x6
    x3.left, x3.right = x7, x8
    x4.right = x9
    x9.left = x10

    print("探索")
    print(r.search(13))  # 13

    print("\n最小値")
    print(r.minimum())  # 2

    print("\n最大値")
    print(r.maximum())  # 20

    print("\n(6の)次節点")
    print(r.search(6).successor())  # 7

    print("\n(6の)前節点")
    print(r.search(6).predecessor())  # 4

    print("\n挿入")
    r.insert(10)  # 10を挿入
    print(r.search(10))  # 確認

    print("\n削除")
    # 子が一つの場合
    print("zが右の子のみをもつ場合")
    print("before:{}".format(r.left.right))
    r = r.search(7).delete()
    print("after:{}".format(r.left.right))

    # 子が二つの場合
    print("\nzが子を二つもつ場合")
    print("before:{}".format(r.left))
    r = r.search(6).delete()
    print("after:{}".format(r.left))

    # ルートの場合
    print("\nzがルートの場合")
    print("before:{}".format(r))
    r = r.delete()
    print("after:{}".format(r))


if __name__ == '__main__':
    main()

動的集合に対する6つの操作

質問（query): 集合𝑆に関する情報を返す操作

  • SEARCH(𝑆,𝑘): 指定したキーを保持する𝑆の要素を返す
  • MINIMUM(𝑆): 最小のキーを保持する𝑆の要素を返す
  • MAXIMUM(𝑆): 最大のキーを保持する𝑆の要素を返す
  • SUCCESSOR(𝑆,𝑥)：要素𝑥を超える𝑆の最小要素を返す
  • PREDECESSOR(𝑆,𝑥): 要素𝑥未満の𝑆の最大要素を返す

変更操作 (modifying operation): 集合を変える操作

  • INSERT(𝑆,𝑥): 集合𝑆に要素𝑥が指す要素を加える操作
  • DELETE(𝑆,𝑥): 集合𝑆から要素𝑥が指す要素を取り除く操作

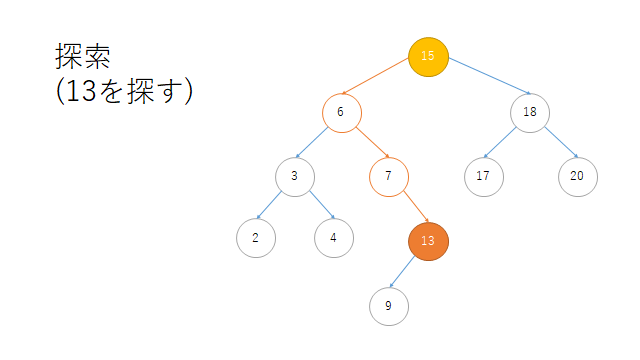
探索(SEARCH)

image.png

メソッド
# 探索
def search(self, k):
    if self is None or k == self.key:
        return self
    if k < self.key:
        return self.left.search(k)
    else:
        return self.right.search(k)

print("探索")              
print(r.search(13))  # 13
結果
探索
Node(13)

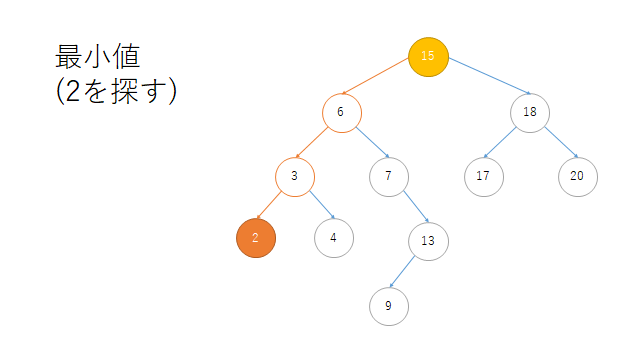
最小値(MINIMUM)

image.png

メソッド
# 最小値  
def minimum(self):          
    while self.left:
        self = self.left    
    return self

print("\n最小値")         
print(r.minimum())  # 2
結果
最小値
Node(2)

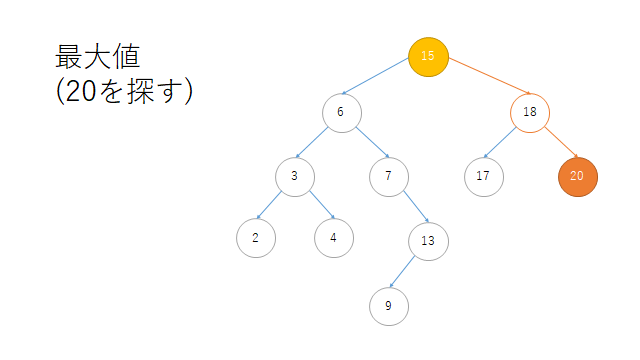
最大値(MAXIMUM)

image.png

メソッド
# 最大値                      
def maximum(self):           
    while self.right:
        self = self.right    
    return self

print("\n最大値")          
print(r.maximum())  # 20
結果
最大値
Node(20)

次節点(SUCCESSOR)

image.png

メソッド
# 次節点                              
def successor(self):               
    if self.right:                 
        return self.right.minimum()
    y = self.p                     
    while y and self == y.right:   
        self = y                   
        y = y.p                    
    return y                       

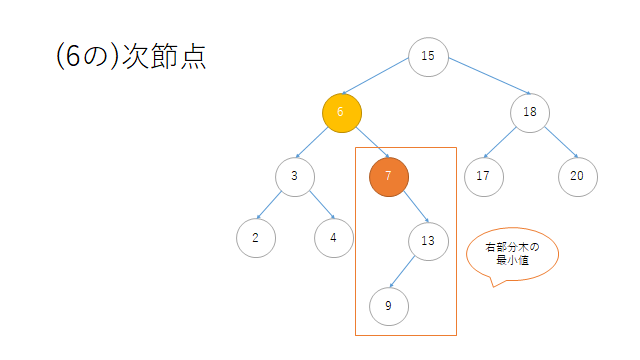
print("\n(6の)次節点")                 
print(r.search(6).successor())  # 7
結果
(6の)次節点
Node(7)

前節点(PREDECESSOR)

image.png

メソッド
# 前節点                             
def predecessor(self):            
    if self.left:                 
        return self.left.maximum()
    y = self.p                    
    while y and self == y.left:   
        self = y                  
        y = y.p                   
    return y                      

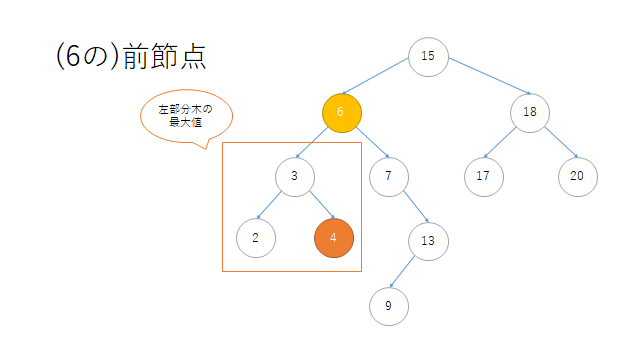
print("\n(6の)前節点")                   
print(r.search(6).predecessor())  # 4
結果
(6の)前節点
Node(4)

挿入(INSERT)

image.png

メソッド
# 二分探索木のルートを返すメソッド           
def root(self):              
    while self.p:            
        self = self.p        
    return self              

# 挿入                         
def insert(self, value):     
    z = Node(value)          
    y = None                 
    self = self.root()       
    while self:              
        y = self             
        if z.key < self.key: 
            self = self.left 
        else:                
            self = self.right
    z.p = y                  
    if y is None:            
        pass                 
    elif z.key < y.key:      
        y.left = z           
    else:                    
        y.right = z          

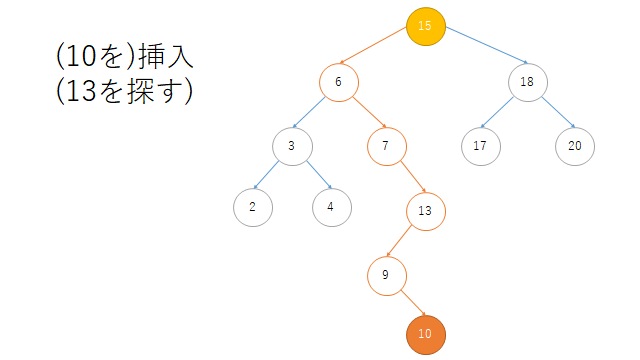
print("\n挿入")            
r.insert(10)  # 10を挿入    
print(r.search(10))  # 確認
結果
挿入
Node(10)

削除(DELETE)

image.png

image.png

メソッド
# 節点(自分)を削除して、子の節点に差し替えるメソッド(deleteメソッドの一部)        
def transparent(self, v):  # selfは削除される節点、vは差し替える節点
    if self.p is None:                             
        pass                                       
    elif self == self.p.left:  # 節点が親の左部分木に属する場合   
        self.p.left = v                            
    else:  # 節点が親の右部分木に属する場合                       
        self.p.right = v                           
    if v:                                          
        v.p = self.p                               

# 削除                                               
def delete(self):                                  
    if self.left is None:  # 右の子のみを持つ場合            
        y = self.right                             
        self.transparent(y)                        
    elif self.right is None:  # 左の子のみを持つ場合         
        y = self.left                              
        self.transparent(y)                        
    else:  # 子を二つ持つ場合                              
        y = self.right.minimum()                   
        if y.p != self:                            
            y.transparent(y.right)                 
            y.right = self.right                   
            y.right.p = y                          
        self.transparent(y)                        
        y.left = self.left                         
        y.left.p = y                               
    return y.root()  # 新しく構成した二分木を返す                     

print("\n削除")                          
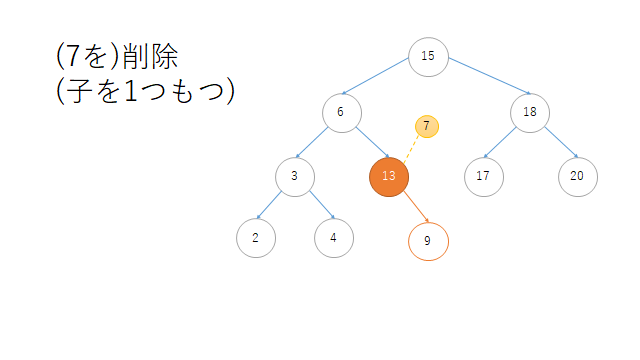
# 子が一つの場合                              
print("zが右の子のみをもつ場合")                  
print("before:{}".format(r.left.right))
r = r.search(7).delete()               
print("after:{}".format(r.left.right)) 

# 子が二つの場合                              
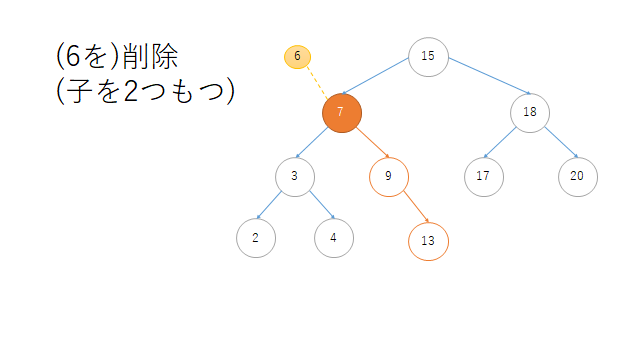
print("\nzが子を二つもつ場合")                  
print("before:{}".format(r.left))      
r = r.search(6).delete()               
print("after:{}".format(r.left))       

# ルートの場合                               
print("\nzがルートの場合")                    
print("before:{}".format(r))           
r = r.delete()                         
print("after:{}".format(r))
結果
削除
zが右の子のみをもつ場合
before:Node(7)
after:Node(13)

zが子を二つもつ場合
before:Node(6)
after:Node(9)

zがルートの場合
before:Node(15)
after:Node(17)
9
5
7

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
9
5