この記事は個人的なお勉強用のメモです。
講義
非線形回帰モデル
線形(=比例)ではないモデル。
例
\begin{align}
y&=w_0+w_1x+w_2x^2+w_3x^3 (3次関数)\\
y&=w_0+w_1 \sin x + w_2 \cos x + w_3 \log x
\end{align}
$x$ をそのままではなく、$\phi(x)$ を使う。
$\phi(x)$ は $x$ の任意の関数。基底関数という。
パラメータ $w$ は線形のまま。
例
\begin{align}
\phi_2(x) &= x^2\\
\phi_3(x) &= x^3\\
\phi_4(x) &= \sin x\\
\phi_5(x) &= \cos x\\
\phi_6(x) &= \log x\\
\end{align}
【重要】以下の式は、$x$ については非線形だが、重み $w$ については線形。
\hat{y}=w_0+w_1\phi_1(x)+w_2\phi_2(x)+...+w_m\phi_m(x)
- 規定展開法
- 回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線形結合を使用
- 未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法により推定
よく使われる基底関数(Φファイ)
- 多項式関数(x_nのような関数)
- ガウス型基底関数(正規分布。$\phi$ ごとに平均 $\mu$ と分散 $\sigma^2$ が異なる)
- スプライン関数 / Bスプライン関数
例えば多項式関数の場合、$m$ を指定する。
$m=3$ の場合、$w_1x^1 + w_2x^2 + w_3x^3$ になる。
上の式は3次式。つまり、3次式のグラフになる。
多項式の場合は、次数によってグラフが変化する。
どれくらい曲線をくねらせたいかによる。
- 説明変数
$x_i=(x_{i1},x_{i2},...,x_{im}) \in R^m$ - 非線形関数ベクトル
$\phi(x_i)=(\phi_1(x_i),\phi_2(x_i),...,\phi_k(x_i))^T \in R^k$
$x_i$ に対して 様々な $\phi()$ を適用する。 - 非線形関数の計画行列
$\Phi=\Bigl(\phi(x_1), \phi(x_2), ..., \phi(x_n)\Bigr)^T \in R^{n\times k}$ - 重み
$\hat{w}=(\Phi^T\Phi)^{-1}\Phi^Ty$
↑ 線形回帰の $X$ が $\Phi$ に変わっただけ。線形回帰での式は $\hat{w}=(X^TX)^{-1}X^Ty$ - 最尤法(最小二乗法)による予測値
$\hat{y}=\Phi(\Phi^{(train)T} \Phi^{(train)})^{-1}\Phi^{(train)T}y^{(train)}$
↑ 線形回帰の $X$ が $\Phi$ に変わっただけ。線形回帰での式は $\hat{y}=X(X^TX)^{-1}X^Ty$
学習の度合い
- 未学習(underfitting)
学習データに対して、十分小さな誤差が得られないモデルのこと。誤差が大きい。
データの構造を充分に表現できていない。
対策:表現力の高いモデルを利用する。 - 過学習(overfitting)
学習データに対しては小さな誤差は得られたが、テストデータでは誤差が大きいモデルのこと。- 対策1:学習データの数を増やす(数の暴力での学習)
- 対策2:不要な基底関数(変数)を削除して表現力を抑止。特徴量選択とも。どこまで削除するのかが難しい。
- 対策3:正則化法を利用して表現力を抑止($w$ を $0$ に近づけたり $0$ にしたり)
ほどよい適切な学習をさせるのが重要。
正則化法
不要な基底関数を削除(上の対策2)
- 基底関数の数、位置やバンド幅によりモデルの複雑さが変化
- 解きたい問題に対して多くの基底関数を用意してしまうと、過学習の問題が起こるため適切な基底関数を用意(CVなどで選択)
- 特徴量の数が多ければ多いほど組み合わせ爆発が起きてしまう。
正則化法(罰則化法)(上の対策3)
- 「モデルの複雑さに伴って、その値が大きくなる正則化項(罰則項)を課した関数」を最小化
- 正則化項(罰則化項)
- 形状によっていくつもの種類があり、それぞれ推定量の性質が異なる
- 正則化(平滑化)パラメータ
- モデルの曲線のなめらかさを調整適切に決める必要あり
S_\gamma=(y-\Phi w)^T (y-\Phi w) + \gamma R(w)
$\gamma$:正則化パラメータ
正則化項(罰則項)の役割
- 無い→最小二乗推定量
- L2ノルムを利用→Ridge推定量
- L1ノルムを利用→LASSO推定量
正則化パラメータの役割
- 小さく→制約面が大きく
- 大きく→制約面が小さく
Ridge推定
パラメータを0に近づけるよう推定
縮小推定という。
あのグラフの意味。
- $x$ 軸は $w_0$、$y$ 軸は $w_1$
- 中央の円は $w_0$ と $w_1$ に対する制約。その範囲内でこれらのパラメータを決定する。
- 右上の楕円は MSE
- 楕円の中央は、MSEの最小値
- MSEの最小値を取るような $w_0$, $w_1$ を選ぶと過学習を起こしてしまう。
- 楕円の年輪みたいなものは、MSEが同じ値を指す等高線のようなもの
- その等高線が中央の円と交わる部分をRidge推定量という
- Ridge推定量の $w_0$, $w_1$ を採用する。
- これらの値は小さいため、入力 $x$ に対する影響を小さくできる。
Ridge推定の場合は、中央の図形は円になる。
正則化パラメータ $\gamma$ の値が変わると、制約の大きさが変わる。
正則化をすると、基底関数が多くても過学習を起こさない。
LASSO推定
いくつかのパラメータを正確に0に推定
意味のないパラメータを使わない、という意味
スパース推定という(スパースとはすかすかという意味)
角の部分=係数が0(図の場合、横軸の値=0、つまり横軸のパラメータは見ない)
LASSO推定の場合は、中央の図形は四角形になる。
モデル選択
モデルを構成する要素
- 基底関数の個数
- 基底関数の位置
- 基底関数のバンド幅(分散の部分とか)
- 正則化パラメータ
いろいろと要素があるが、最適なモデルを作成するには、交差検証法で決定する。
ホールドアウト法
- データを学習用とテスト用に分割(例:70%を学習用、30%をテスト用)
- データの交換はしない
- データが少ない場合に問題が起きやすい(外れ値が学習用に含まれるとそれを学習してしまう)
クロスバリデーション(交差検証)
- データを学習用とテスト用に分割
- それを繰り返す(5回繰り返すと、5つモデルができる、それぞれで精度検証する)
- 精度の平均をCV(Cross Validation)値と呼ぶ
- CV値の小さなモデルを採用する
グリッドサーチ
- ハイパーパラメータはあらかじめ決めて必要がある場合がある(「ハイパラ調整」)。
- $\lambda$ と $m$ というパラメータがある場合、それぞれの値の組み合わせを確かめる。これをグリッドサーチという。
- 各パラメータに与える値は候補を用意する。
実装演習
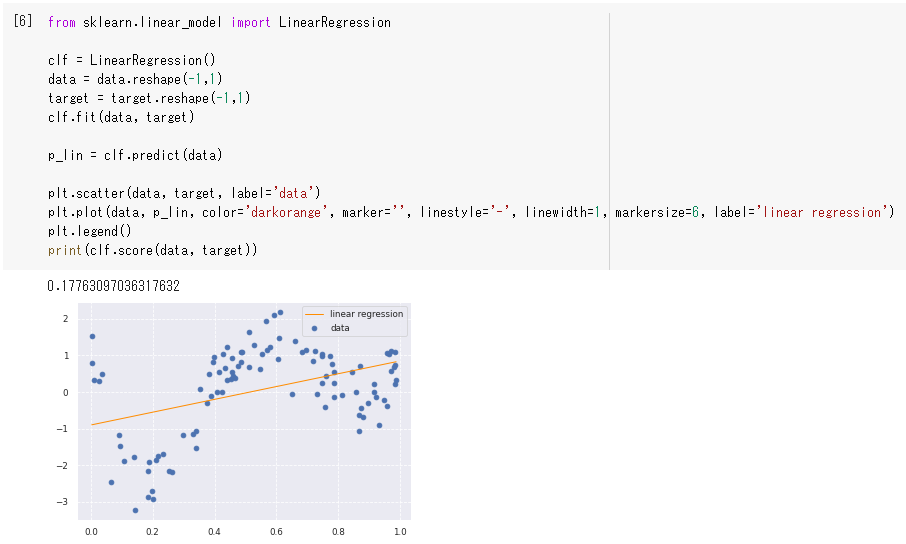
線形回帰モデル(LinearRegression)の場合、スコア(0.177)も低く、
学習できていないことがグラフからも明らか。
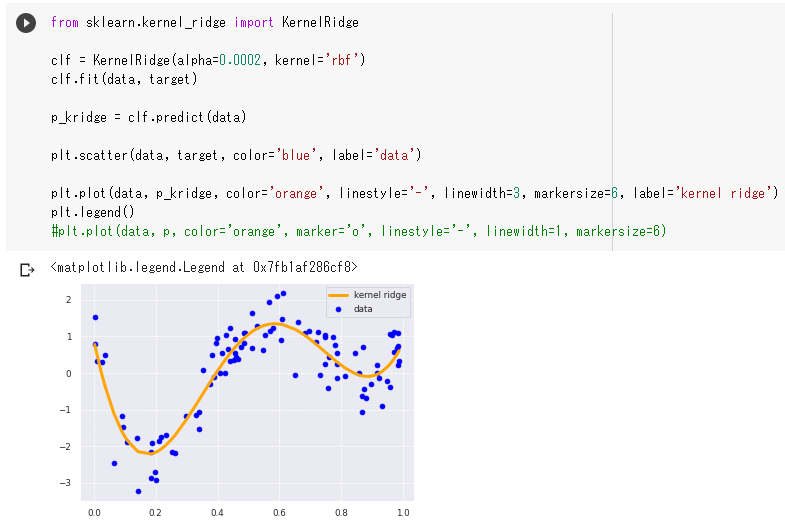
KernelRidgeクラスを用いてkernelパラメータにrbfを与えている。
rbfを与えると放射基底関数(Radial basis function)という基底関数が採用される模様。
ネット上にあるグラフを見る限りでは、正規分布のようなグラフをしている。
このような非線形回帰モデルの場合、曲線となって学習用データの間をほどよく通っている。
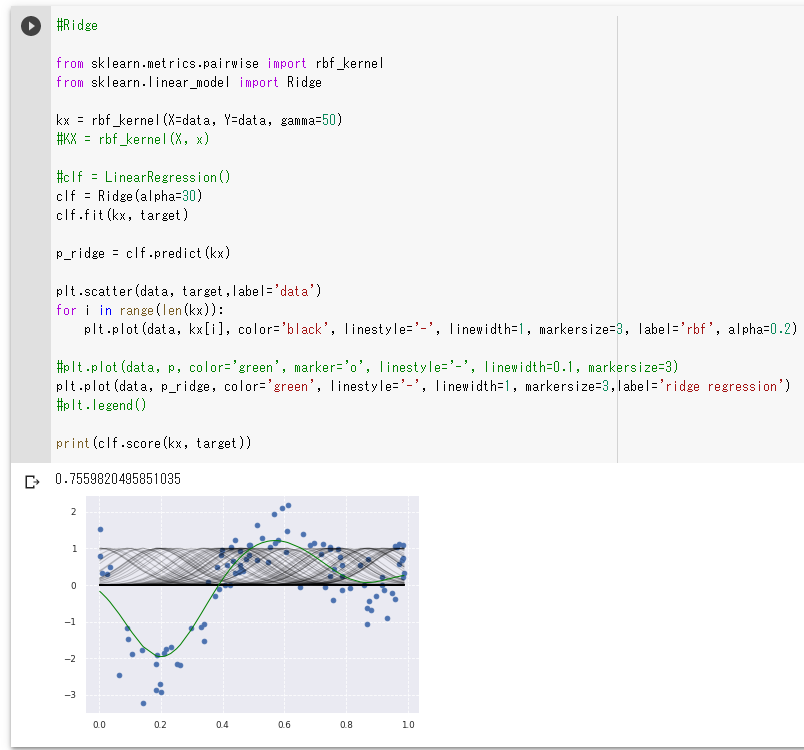
Ridge回帰。
上のグラフではほどよく学習できている。
指定している数値のパラメータは次のとおり。
- rbf_kernel関数のgammaパラメータ(値は50)
- Ridgeクラスのalphaパラメータ(値は30)
gammaを500にしたところ、グラフがヨレヨレになって
まるで過学習を起こしたかのようなグラフになった。
しかし、あまり学習用のデータを通らない。
これは過学習とは言わないのか。
gammaを5にしたところ、緩やかな曲線になった。
gammaを50に戻して、alphaを300にしたところ、
緩やかな曲線になった。
alphaを3にしたところ、30のときと大きく変わりはない。
いずれも正則化パラメータであり、適切な値を指定する必要であることがわかる。
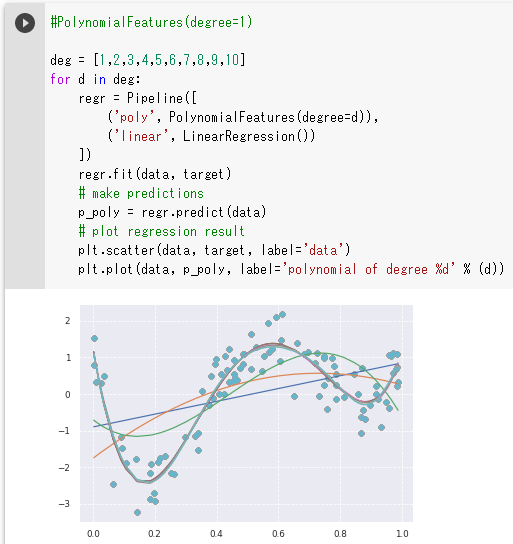
非線形回帰。
PolynomialFeaturesクラスによって、1乗から9乗までの多項式を作成している。
このグラフは講義の中でも出てきたが、4乗以上では曲線が重なっており
5乗以上のモデルを作る意味はなさそうに見える。
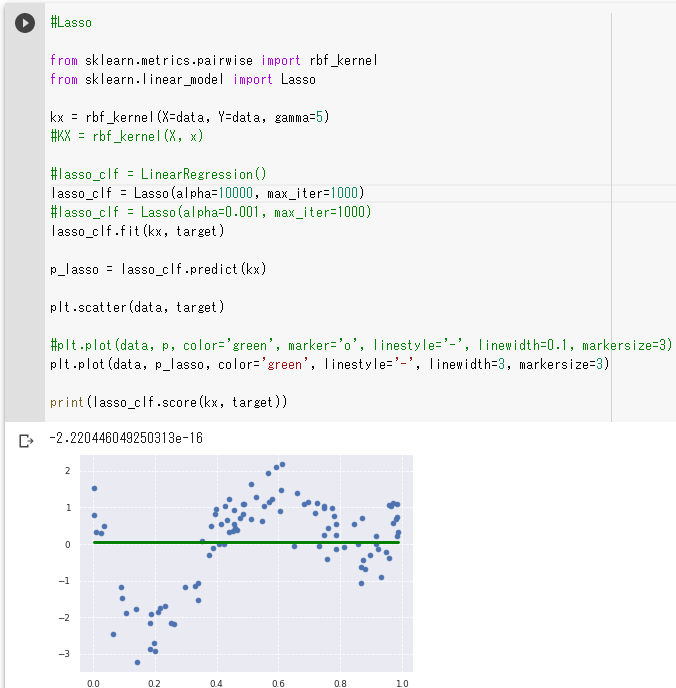
LASSO回帰。
上のグラフは配布されているソースをそのまま実行した結果。
Lassoクラスのalphaパラメータに10000が指定されており、直線になっている。
これは極度に汎化性能が高い状態。
このalphaパラメータを0.001くらいにすると、ほどよい曲線になった。
演習問題(修了テスト~練習問題~)
問題11(k-分割交差検証)
k-分割交差検証(K-fold cross-validation)
- データセットをk個の重複しない集合に分割
- k-1個の集合は訓練データ
- 残りの1個の集合は検証用データ
- これをk回繰り返して、平均をとる
問題12(k-分割交差検証)
利点
- サイズの小さいデータセットを活用できる。
- 繰り返し学習と評価を行うことで、過学習を防ぐ。
問題13(k-分割交差検証)
欠点
- k回繰り返して学習と評価を行うため、計算時間がかかる。
問題32(L1正則化の式)
L1ノルムに基づいて絶対値の足し算をする。(マンハッタン距離の足し算)
これに正則化パラメータ $\lambda$ を掛ける。$\lambda$ は外部から与える。
掛けた値を元の式に加える。
よって、損失関数 $C'(W)$ をL1正則化した式はこちら。
C'(W)=C(W)+\lambda (|w_1|+|w_2|+,..,+|w_n|)
問題33(L1正則化の特徴)
- L1正則化すると、係数が0になるため、モデルの解釈はしやすくなる。
- L1正則化すると、要素に0を含むことが多くなる。これをスパース(すかすか)という。
- L1正則化はLASSO正則化とも呼ばれる。Ridge正則化はL2正則化。
- 正則化パラメータ $\lambda$ を大きくすると、重みが大きくなることへのペナルティが重くなる。
問題34(L1正則化の実装)
L1正則化は、絶対値の足し算。
すべての行を足してスカラー値を出力する必要があるので、axisの指定はしない。
axis=0を指定すると、縦方向に足し算された行列が出力される。
axis=1を指定すると、横方向に足し算された行列が出力される。
loss = loss_function(t,y) + weight_delay_lambda * np.sum(np.abs(W))
問題35(L2正則化の式)
L2ノルム(ユークリッド距離)を求める。
正則化パラメータを掛ける。
元の式に加える。
C'(W)=C(W)+\frac{1}{2}\lambda \sqrt{(w_1^2+w_2^2+,...+w_n^2)}
上の式には $\lambda$ の前に $\frac{1}{2}$ が付いているが、
付いていない場合もあるとのこと。
問題36(L2正則化の特徴)
- L2正則化を加えると、訓練データに対する認識制度は低くなる(代わりに汎化性能が上がる)。
- L2正則化を加えると、重み $W$ の大きさが小さくなり、汎化性能が高くなる。
- L2正則化を加えると、重み $W$ に $0$ の要素が多くなりやすい。(正確には、$0$ に近い要素が多くなりやすい)